第二十三章 旋转 学情评估卷(含答案)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章 旋转 学情评估卷(含答案)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 00:00:00 | ||
图片预览


文档简介
第二十三章 旋转 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运动属于数学上的旋转的是( )
A. 钟表上时针的运动
B. 笔直道路上公共汽车的运动
C. 电梯由1楼上升到6楼
D. 将等腰三角形沿着底边上的高对折
2.剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称图形又是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
3.如图,将绕点顺时针旋转 得到,连接.若线段,则( )
(第3题)
A. 2 B. 3 C. 4 D. 5
4.如图,将矩形绕点逆时针旋转得到矩形,已知 ,则的度数为( )
(第4题)
A. B. C. D.
5.如图,在平面直角坐标系中,若将以某点为旋转中心,顺时针旋转 得到,其中的对应点是,的对应点是,则旋转中心的坐标是( )
(第5题)
A. B. C. D.
6.在平面直角坐标系中,已知点,关于原点对称,则,的值分别是( )
A. ,2 B. 1,2 C. , D. 1,
7.如图,线段与相交于点,且,则下列结论中正确的个数是( )
(第7题)
;
;
③线段与关于点成中心对称;
和关于点成中心对称.
A. 4 B. 3 C. 2 D. 1
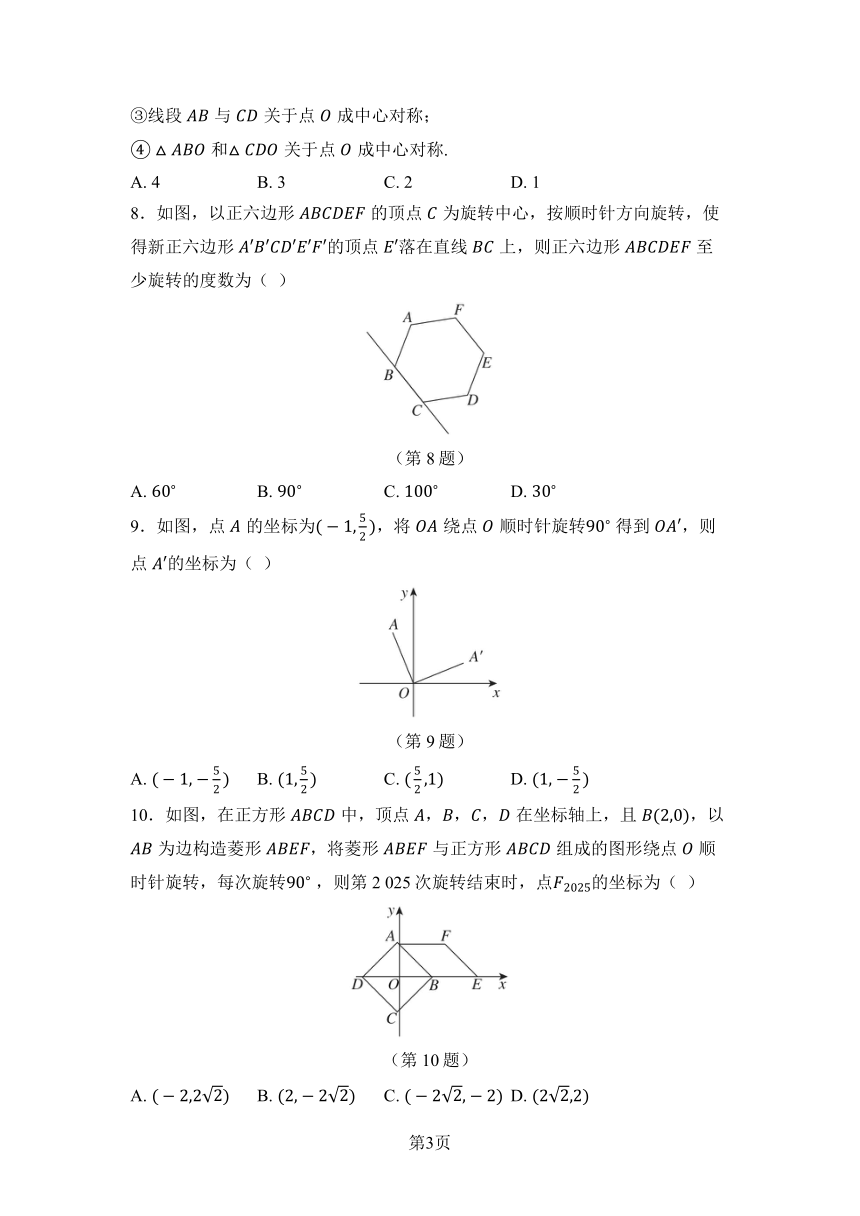
8.如图,以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转的度数为( )
(第8题)
A. B. C. D.
9.如图,点的坐标为,将绕点顺时针旋转 得到,则点的坐标为( )
(第9题)
A. B. C. D.
10.如图,在正方形中,顶点,,,在坐标轴上,且,以为边构造菱形,将菱形与正方形组成的图形绕点顺时针旋转,每次旋转 ,则第2 025次旋转结束时,点的坐标为( )
(第10题)
A. B. C. D.
二、填空题(本大题共3小题,每小题4分,共12分)
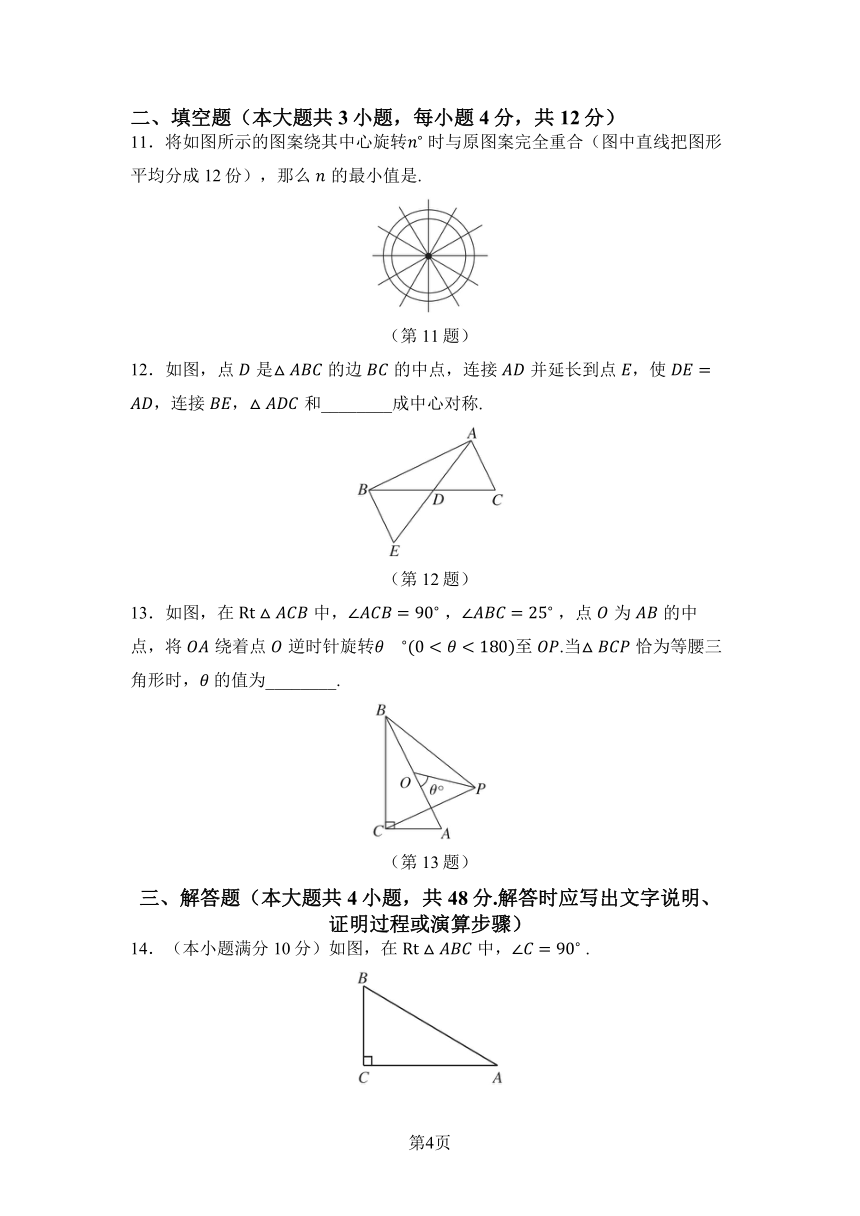
11.将如图所示的图案绕其中心旋转 时与原图案完全重合(图中直线把图形平均分成12份),那么的最小值是.
(第11题)
12.如图,点是的边的中点,连接并延长到点,使,连接,和_ _ _ _ _ _ _ _ 成中心对称.
(第12题)
13.如图,在中, , ,点为的中点,将绕着点逆时针旋转至.当恰为等腰三角形时, 的值为_ _ _ _ _ _ _ _ .
(第13题)
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分10分)如图,在中, .
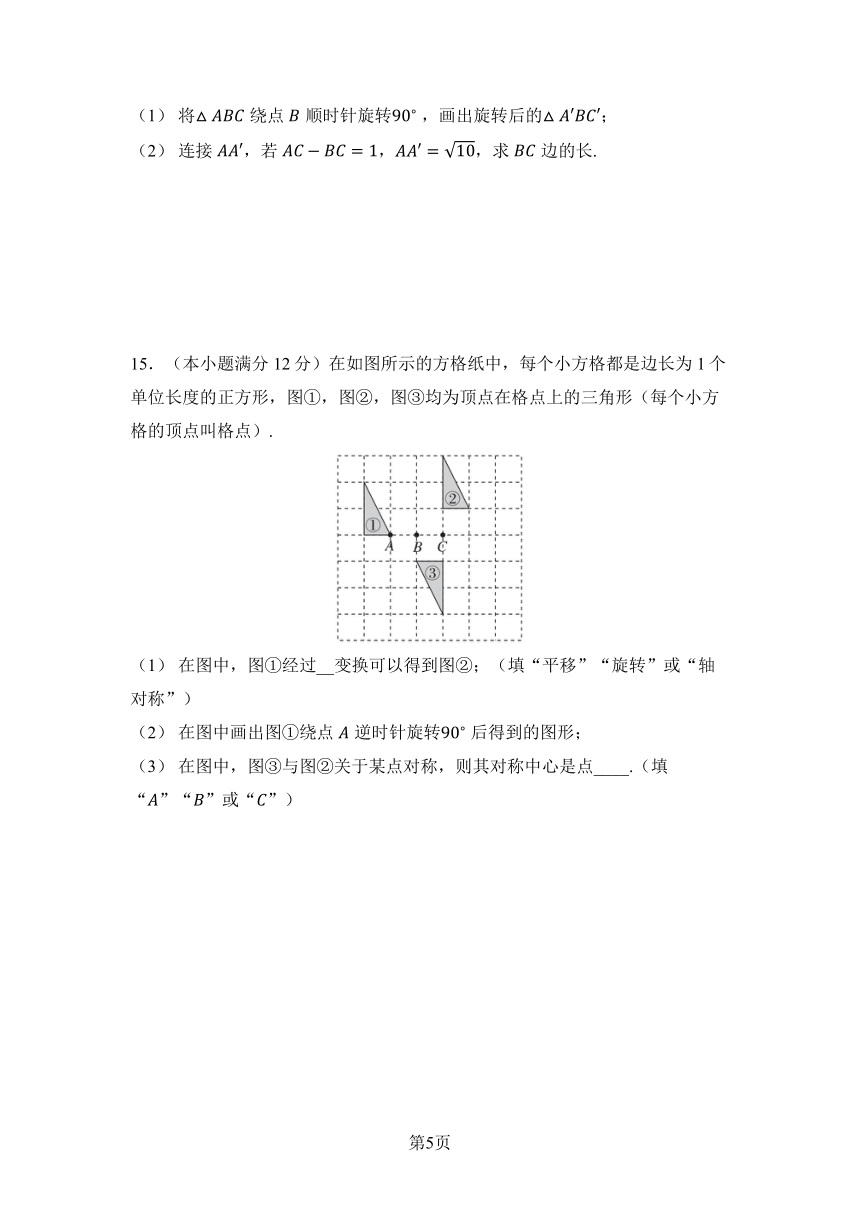
(1) 将绕点顺时针旋转 ,画出旋转后的;
(2) 连接,若,,求边的长.
15.(本小题满分12分)在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图①,图②,图③均为顶点在格点上的三角形(每个小方格的顶点叫格点).
(1) 在图中,图①经过_ _ 变换可以得到图②;(填“平移”“旋转”或“轴对称”)
(2) 在图中画出图①绕点逆时针旋转 后得到的图形;
(3) 在图中,图③与图②关于某点对称,则其对称中心是点_ _ _ _ .(填“”“”或“”)
16.(本小题满分12分)如图,在中,两条对角线,相交于点,,以为边向下方作菱形.
(1) 判断四边形的形状,并说明理由;
(2) 若菱形的周长为16, ,点是菱形的对称中心,求点,之间的距离.
17.(本小题满分14分)将绕点顺时针旋转得到,并使点的对应点落在直线上.
(1) 如图①,证明:平分;
(2) 如图②,与交于点,若 , ,求的度数;
(3) 如图③,连接,若,,,则的长为_ _ _ _ _ _ _ _ _ _ _ _ .
第二十三章 旋转 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运动属于数学上的旋转的是( )
A. 钟表上时针的运动
B. 笔直道路上公共汽车的运动
C. 电梯由1楼上升到6楼
D. 将等腰三角形沿着底边上的高对折
【答案】A
2.剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称图形又是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
【答案】A
3.如图,将绕点顺时针旋转 得到,连接.若线段,则( )
(第3题)
A. 2 B. 3 C. 4 D. 5
【答案】C
4.如图,将矩形绕点逆时针旋转得到矩形,已知 ,则的度数为( )
(第4题)
A. B. C. D.
【答案】C
5.如图,在平面直角坐标系中,若将以某点为旋转中心,顺时针旋转 得到,其中的对应点是,的对应点是,则旋转中心的坐标是( )
(第5题)
A. B. C. D.
【答案】C
6.在平面直角坐标系中,已知点,关于原点对称,则,的值分别是( )
A. ,2 B. 1,2 C. , D. 1,
【答案】A
7.如图,线段与相交于点,且,则下列结论中正确的个数是( )
(第7题)
;
;
③线段与关于点成中心对称;
和关于点成中心对称.
A. 4 B. 3 C. 2 D. 1
【答案】A
8.如图,以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转的度数为( )
(第8题)
A. B. C. D.
【答案】B
9.如图,点的坐标为,将绕点顺时针旋转 得到,则点的坐标为( )
(第9题)
A. B. C. D.
【答案】C
10.如图,在正方形中,顶点,,,在坐标轴上,且,以为边构造菱形,将菱形与正方形组成的图形绕点顺时针旋转,每次旋转 ,则第2 025次旋转结束时,点的坐标为( )
(第10题)
A. B. C. D.
【答案】B
二、填空题(本大题共3小题,每小题4分,共12分)
11.将如图所示的图案绕其中心旋转 时与原图案完全重合(图中直线把图形平均分成12份),那么的最小值是.
(第11题)
【答案】30
12.如图,点是的边的中点,连接并延长到点,使,连接,和_ _ _ _ _ _ _ _ 成中心对称.
(第12题)
【答案】
13.如图,在中, , ,点为的中点,将绕着点逆时针旋转至.当恰为等腰三角形时, 的值为_ _ _ _ _ _ _ _ .
(第13题)
【答案】50或65或80
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分10分)如图,在中, .
(1) 将绕点顺时针旋转 ,画出旋转后的;
(2) 连接,若,,求边的长.
【答案】
(1) 解:如图,即为所求.
(2) 如图,设,则.
在中,.
由旋转的性质,得
, .
在中,.
因为,
所以.
即.
解得,(舍去).
所以.
15.(本小题满分12分)在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图①,图②,图③均为顶点在格点上的三角形(每个小方格的顶点叫格点).
(1) 在图中,图①经过_ _ 变换可以得到图②;(填“平移”“旋转”或“轴对称”)
(2) 在图中画出图①绕点逆时针旋转 后得到的图形;
(3) 在图中,图③与图②关于某点对称,则其对称中心是点_ _ _ _ .(填“”“”或“”)
【答案】(1) 平移
(2) 解:图①绕点逆时针旋转 后得到的图形如图所示.
(3)
16.(本小题满分12分)如图,在中,两条对角线,相交于点,,以为边向下方作菱形.
(1) 判断四边形的形状,并说明理由;
(2) 若菱形的周长为16, ,点是菱形的对称中心,求点,之间的距离.
【答案】
(1) 解:四边形是矩形.
理由如下:
四边形是平行四边形,, 四边形是矩形.
(2) 菱形的周长为16,
.
由(1)知四边形为矩形,
,.
,,
.
点是菱形的对称中心,
点,之间的距离等于点到点的距离,即点,之间的距离等于2.
17.(本小题满分14分)将绕点顺时针旋转得到,并使点的对应点落在直线上.
(1) 如图①,证明:平分;
(2) 如图②,与交于点,若 , ,求的度数;
(3) 如图③,连接,若,,,则的长为_ _ _ _ _ _ _ _ _ _ _ _ .
【答案】
(1) 证明:由旋转的性质,
得,,
,,平分.
(2) 解:设 ,
则 .
,
.
, ,解得, .
(3)
第页
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运动属于数学上的旋转的是( )
A. 钟表上时针的运动
B. 笔直道路上公共汽车的运动
C. 电梯由1楼上升到6楼
D. 将等腰三角形沿着底边上的高对折
2.剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称图形又是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
3.如图,将绕点顺时针旋转 得到,连接.若线段,则( )
(第3题)
A. 2 B. 3 C. 4 D. 5
4.如图,将矩形绕点逆时针旋转得到矩形,已知 ,则的度数为( )
(第4题)
A. B. C. D.
5.如图,在平面直角坐标系中,若将以某点为旋转中心,顺时针旋转 得到,其中的对应点是,的对应点是,则旋转中心的坐标是( )
(第5题)
A. B. C. D.
6.在平面直角坐标系中,已知点,关于原点对称,则,的值分别是( )
A. ,2 B. 1,2 C. , D. 1,
7.如图,线段与相交于点,且,则下列结论中正确的个数是( )
(第7题)
;
;
③线段与关于点成中心对称;
和关于点成中心对称.
A. 4 B. 3 C. 2 D. 1
8.如图,以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转的度数为( )
(第8题)
A. B. C. D.
9.如图,点的坐标为,将绕点顺时针旋转 得到,则点的坐标为( )
(第9题)
A. B. C. D.
10.如图,在正方形中,顶点,,,在坐标轴上,且,以为边构造菱形,将菱形与正方形组成的图形绕点顺时针旋转,每次旋转 ,则第2 025次旋转结束时,点的坐标为( )
(第10题)
A. B. C. D.
二、填空题(本大题共3小题,每小题4分,共12分)
11.将如图所示的图案绕其中心旋转 时与原图案完全重合(图中直线把图形平均分成12份),那么的最小值是.
(第11题)
12.如图,点是的边的中点,连接并延长到点,使,连接,和_ _ _ _ _ _ _ _ 成中心对称.
(第12题)
13.如图,在中, , ,点为的中点,将绕着点逆时针旋转至.当恰为等腰三角形时, 的值为_ _ _ _ _ _ _ _ .
(第13题)
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分10分)如图,在中, .
(1) 将绕点顺时针旋转 ,画出旋转后的;
(2) 连接,若,,求边的长.
15.(本小题满分12分)在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图①,图②,图③均为顶点在格点上的三角形(每个小方格的顶点叫格点).
(1) 在图中,图①经过_ _ 变换可以得到图②;(填“平移”“旋转”或“轴对称”)
(2) 在图中画出图①绕点逆时针旋转 后得到的图形;
(3) 在图中,图③与图②关于某点对称,则其对称中心是点_ _ _ _ .(填“”“”或“”)
16.(本小题满分12分)如图,在中,两条对角线,相交于点,,以为边向下方作菱形.
(1) 判断四边形的形状,并说明理由;
(2) 若菱形的周长为16, ,点是菱形的对称中心,求点,之间的距离.
17.(本小题满分14分)将绕点顺时针旋转得到,并使点的对应点落在直线上.
(1) 如图①,证明:平分;
(2) 如图②,与交于点,若 , ,求的度数;
(3) 如图③,连接,若,,,则的长为_ _ _ _ _ _ _ _ _ _ _ _ .
第二十三章 旋转 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列运动属于数学上的旋转的是( )
A. 钟表上时针的运动
B. 笔直道路上公共汽车的运动
C. 电梯由1楼上升到6楼
D. 将等腰三角形沿着底边上的高对折
【答案】A
2.剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称图形又是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
【答案】A
3.如图,将绕点顺时针旋转 得到,连接.若线段,则( )
(第3题)
A. 2 B. 3 C. 4 D. 5
【答案】C
4.如图,将矩形绕点逆时针旋转得到矩形,已知 ,则的度数为( )
(第4题)
A. B. C. D.
【答案】C
5.如图,在平面直角坐标系中,若将以某点为旋转中心,顺时针旋转 得到,其中的对应点是,的对应点是,则旋转中心的坐标是( )
(第5题)
A. B. C. D.
【答案】C
6.在平面直角坐标系中,已知点,关于原点对称,则,的值分别是( )
A. ,2 B. 1,2 C. , D. 1,
【答案】A
7.如图,线段与相交于点,且,则下列结论中正确的个数是( )
(第7题)
;
;
③线段与关于点成中心对称;
和关于点成中心对称.
A. 4 B. 3 C. 2 D. 1
【答案】A
8.如图,以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转的度数为( )
(第8题)
A. B. C. D.
【答案】B
9.如图,点的坐标为,将绕点顺时针旋转 得到,则点的坐标为( )
(第9题)
A. B. C. D.
【答案】C
10.如图,在正方形中,顶点,,,在坐标轴上,且,以为边构造菱形,将菱形与正方形组成的图形绕点顺时针旋转,每次旋转 ,则第2 025次旋转结束时,点的坐标为( )
(第10题)
A. B. C. D.
【答案】B
二、填空题(本大题共3小题,每小题4分,共12分)
11.将如图所示的图案绕其中心旋转 时与原图案完全重合(图中直线把图形平均分成12份),那么的最小值是.
(第11题)
【答案】30
12.如图,点是的边的中点,连接并延长到点,使,连接,和_ _ _ _ _ _ _ _ 成中心对称.
(第12题)
【答案】
13.如图,在中, , ,点为的中点,将绕着点逆时针旋转至.当恰为等腰三角形时, 的值为_ _ _ _ _ _ _ _ .
(第13题)
【答案】50或65或80
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分10分)如图,在中, .
(1) 将绕点顺时针旋转 ,画出旋转后的;
(2) 连接,若,,求边的长.
【答案】
(1) 解:如图,即为所求.
(2) 如图,设,则.
在中,.
由旋转的性质,得
, .
在中,.
因为,
所以.
即.
解得,(舍去).
所以.
15.(本小题满分12分)在如图所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,图①,图②,图③均为顶点在格点上的三角形(每个小方格的顶点叫格点).
(1) 在图中,图①经过_ _ 变换可以得到图②;(填“平移”“旋转”或“轴对称”)
(2) 在图中画出图①绕点逆时针旋转 后得到的图形;
(3) 在图中,图③与图②关于某点对称,则其对称中心是点_ _ _ _ .(填“”“”或“”)
【答案】(1) 平移
(2) 解:图①绕点逆时针旋转 后得到的图形如图所示.
(3)
16.(本小题满分12分)如图,在中,两条对角线,相交于点,,以为边向下方作菱形.
(1) 判断四边形的形状,并说明理由;
(2) 若菱形的周长为16, ,点是菱形的对称中心,求点,之间的距离.
【答案】
(1) 解:四边形是矩形.
理由如下:
四边形是平行四边形,, 四边形是矩形.
(2) 菱形的周长为16,
.
由(1)知四边形为矩形,
,.
,,
.
点是菱形的对称中心,
点,之间的距离等于点到点的距离,即点,之间的距离等于2.
17.(本小题满分14分)将绕点顺时针旋转得到,并使点的对应点落在直线上.
(1) 如图①,证明:平分;
(2) 如图②,与交于点,若 , ,求的度数;
(3) 如图③,连接,若,,,则的长为_ _ _ _ _ _ _ _ _ _ _ _ .
【答案】
(1) 证明:由旋转的性质,
得,,
,,平分.
(2) 解:设 ,
则 .
,
.
, ,解得, .
(3)
第页
同课章节目录
