2025年甘肃省武威第二十中学中考数学人教版 多边形及其内角和 专项练习题(含答案)
文档属性
| 名称 | 2025年甘肃省武威第二十中学中考数学人教版 多边形及其内角和 专项练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 15:26:24 | ||
图片预览


文档简介
2025年甘肃省武威第二十中学中考数学人教版《多边形及其内角和》专项练习题
一、单选题
1.如图,是四边形的对角线,且四边形的内角和为,与的内角和相加为n,则( )
A. B. C. D.无法比较m,n大小关系
2.如图,直线,正五边形的边在直线上,顶点在直线上,过点作正五边形的对称轴分别交,,于点,,,则的度数为( )
A. B. C. D.
3. 是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A. B. C. D.
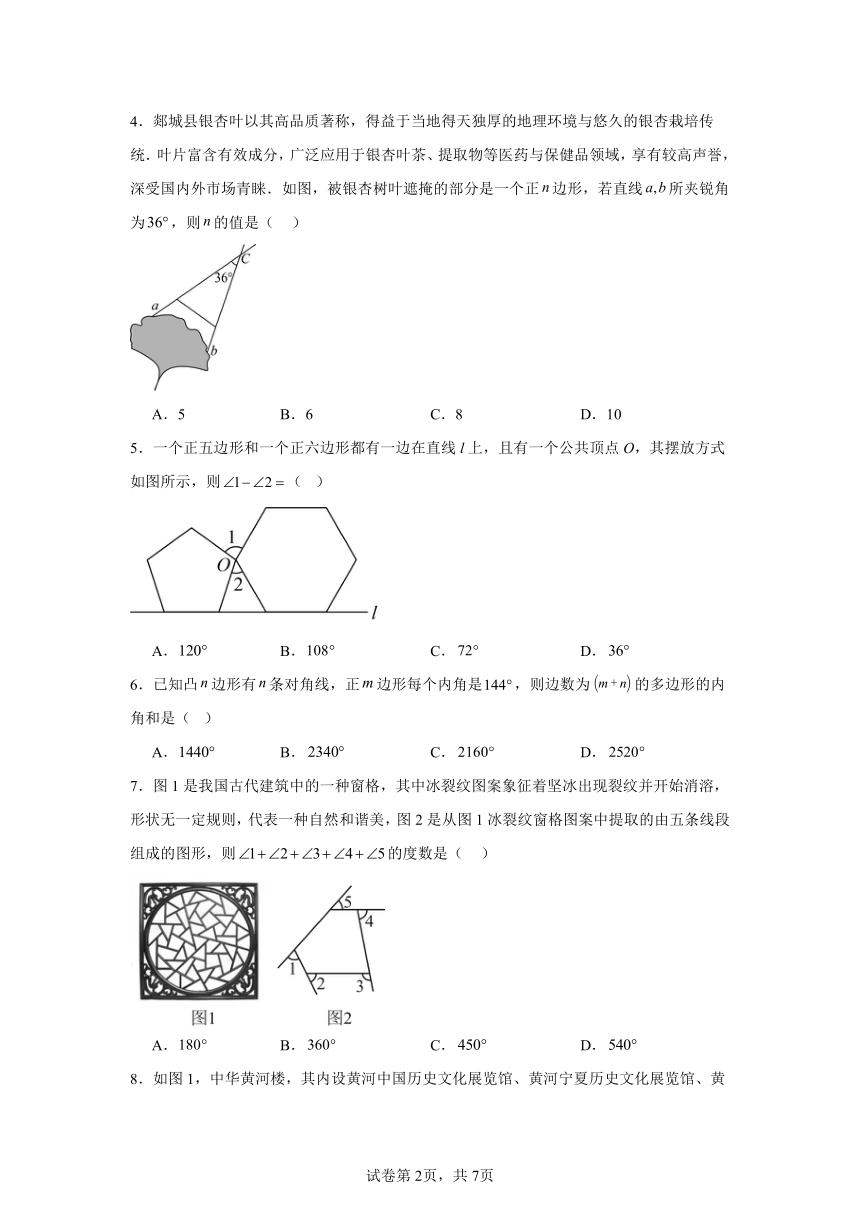
4.郯城县银杏叶以其高品质著称,得益于当地得天独厚的地理环境与悠久的银杏栽培传统.叶片富含有效成分,广泛应用于银杏叶茶、提取物等医药与保健品领域,享有较高声誉,深受国内外市场青睐.如图,被银杏树叶遮掩的部分是一个正边形,若直线所夹锐角为,则的值是( )
A.5 B.6 C.8 D.10
5.一个正五边形和一个正六边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则( )
A. B. C. D.
6.已知凸边形有条对角线,正边形每个内角是,则边数为的多边形的内角和是( )
A. B. C. D.
7.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美,图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则的度数是( )
A. B. C. D.
8.如图1,中华黄河楼,其内设黄河中国历史文化展览馆、黄河宁夏历史文化展览馆、黄河印象展览馆、黄河文化演艺厅等.是全方位展示黄河五千年灿烂文明的博物馆、黄河文化汇宁夏的重要载体和西部乃至全国的知名旅游景点.是宁夏黄河金岸的点晴之笔和标志性的景观工程之一,如图2是黄河楼台基底层正多边形的部分示意图,其外角为,则该正多边形是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
9.如图,,的角平分线的反向延长线和的角平分线交于点,,则( )
A. B. C. D.
二、填空题
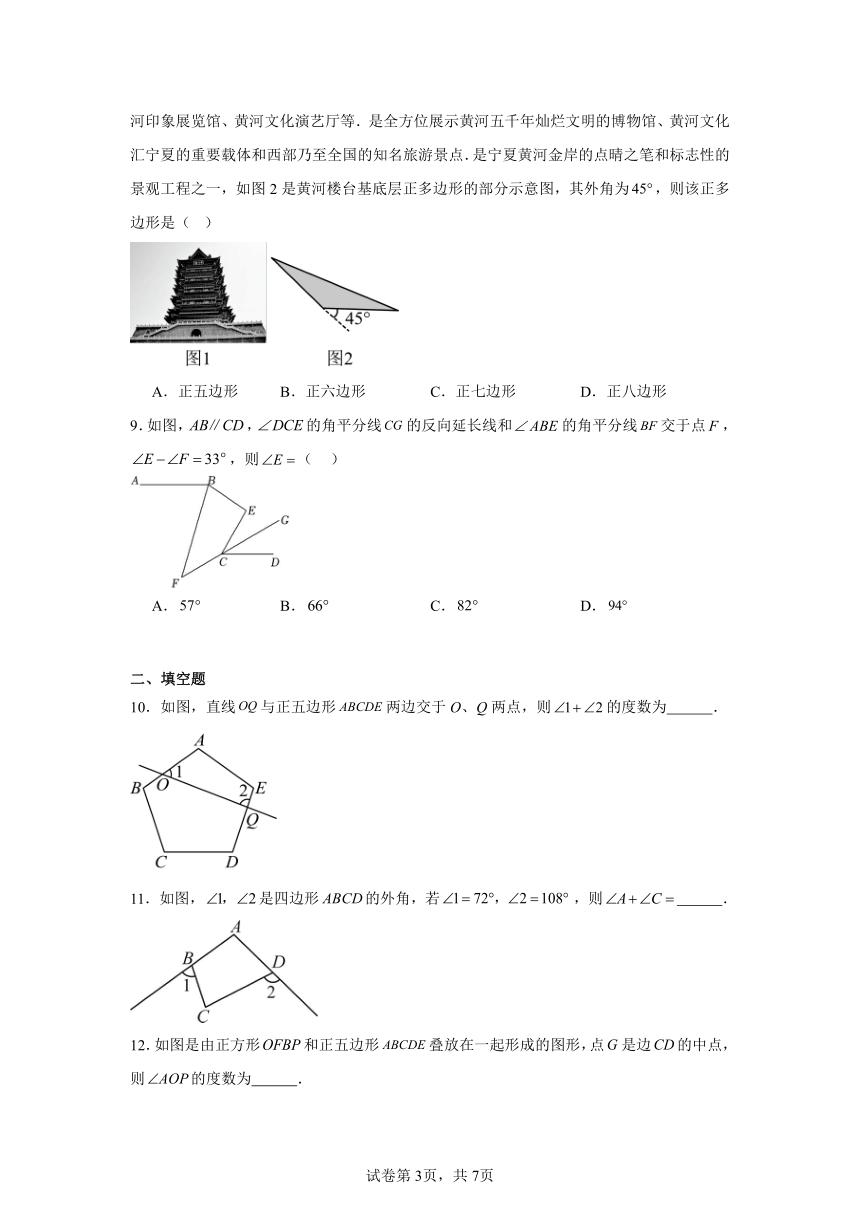
10.如图,直线与正五边形两边交于O、Q两点,则的度数为 .
11.如图,是四边形的外角,若,则 .
12.如图是由正方形和正五边形叠放在一起形成的图形,点是边的中点,则的度数为 .
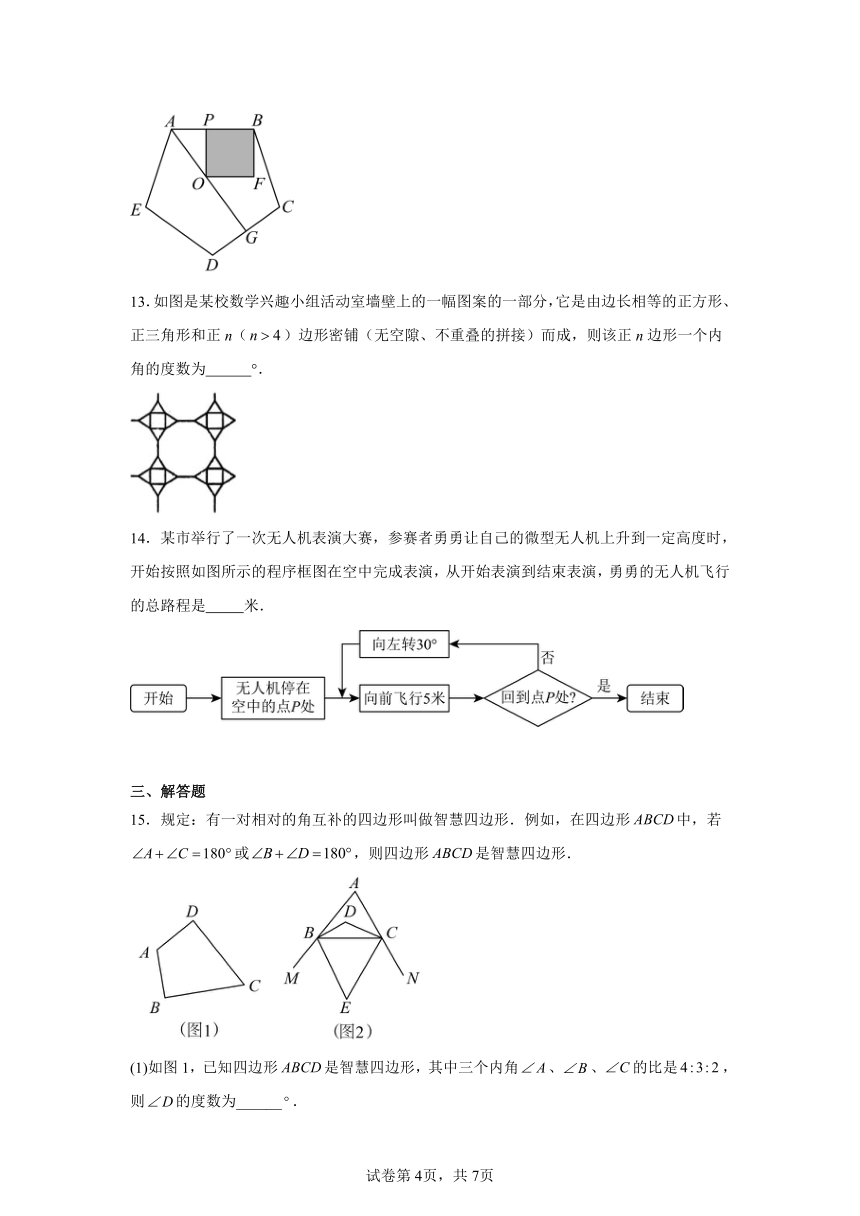
13.如图是某校数学兴趣小组活动室墙壁上的一幅图案的一部分,它是由边长相等的正方形、正三角形和正n()边形密铺(无空隙、不重叠的拼接)而成,则该正n边形一个内角的度数为 °.
14.某市举行了一次无人机表演大赛,参赛者勇勇让自己的微型无人机上升到一定高度时,开始按照如图所示的程序框图在空中完成表演,从开始表演到结束表演,勇勇的无人机飞行的总路程是 米.
三、解答题
15.规定:有一对相对的角互补的四边形叫做智慧四边形.例如,在四边形中,若或,则四边形是智慧四边形.
(1)如图1,已知四边形是智慧四边形,其中三个内角、、的比是,则的度数为______.
(2)如图2,D为△ABC内一点,且,△ABC的两个外角、的角平分线交于点E,判断四边形是否为智慧四边形,并说明理由.
16.已知:多边形的外角和的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图①,,BM与DN交于点P,求的度数;
②如图②,猜测当和满足什么数量关系时,,并证明你的猜想.
(2)如图③,若多边形是五边形ABCDG,已知,BM与DN交于点P,求的度数.
17.探究一:
已知:如图(1),在中,分别平分和,试探究与的数量关系.并说明理由.
探究二:
若将改为任意四边形呢?
已知:如图(2),在四边形中,分别平分和,请你利用上述结论探究与的数量关系,并说明理由.
探究三:若将上题中的四边形改为六边形如图(3)所示,请你直接写出与的数量关系.
18.如图1,图2,在四边形中,是四边形的一个外角.
(1)四边形的外角和为________度;
(2)如图1,图2,已知.
①如图1,求证:;
②如图2,若平分,交于点G,平分,且与相交于点F,试判断与之间的位置关系,并说明理由.
19.小东在学习中遇到这样一个问题:如图1,△ABC中,平分,平分外角.猜想与的数量关系.
(1)小东阅读题目后,没有发现数量关系与解题思路,于是尝试代入的值求的值,
①如果,则的度数为_____;如果,则的度数为_____.
②请猜想与的数量关系,并说明理由.
(2)小东继续探究,如图2,在四边形中,平分,且与四边形的外角的平分线交于点.若,,则的度数为_____.
(3)小东又思考,改变,的大小,如图3,在四边形中,四边形的内角的角平分线所在的直线与外角的角平分线所在的直线相交于点,若,,则可表示为_____.(请用含α、β的表达式表示)
20.定义:有一组对角互补的四边形叫做对补四边形.
(1)已知四边形是对补四边形.
①若,则 .
②如图①,的平分线分别与相交于点E、F,求证:;
(2)如图②,在四边形中,对角线,交于点E,且平分,,平分,与交于点F,且于点G,则四边形是对补四边形吗?请说明理由;
(3)已知四边形是对补四边形,其三个顶点A,B,D如图③所示,连接,.若平分,平分,且直线,交于点O(与点C不重合),请直接写出与之间的数量关系.
21.小亮学习了“多边形及其内角和”后,对几何学习产生了浓厚的兴趣,三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系.
【探究发现】
(1)如图①,在中,、分别平分和,试探究与的数量关系.并说明理由.
【拓展延伸】
(2)如图②,在四边形中,分别平分和,请你探究与之间的数量关系,并说明理由.
【类比迁移】
(3)若将(2)中的四边形改为六边形,如图③,请你探究与之间的数量关系,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《多边形及其内角和》专项练习题》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 B A A A D B B D C
10./144度
11.
12./度
13.150
15.(1)
(2)四边形为智慧四边形,理由见解析
16.(1)①∵,
∴在四边形ABCD中,,
,
∵多边形的外角和的平分线分别为BM,DN,
∴,
;
②当时,,
证明:如图,连接,
∵,
,
,
即,
,
,
∴;
(2)如图,延长交于点Q,
∵,,
,
∴,
∵平分,平分,
,
,
,
.
17.解:探究一:,理由如下:
解:∵分别平分和,
∴,
∴,
,
,
,
;
探究二:,理由如下:
∵分别平分和,
∴,
∴,
,
,
,
;
探究三:六边形的内角和为:,
∵分别平分和,
∴,
∴,
,
,
,
,
即.
18.(1)解:四边形的外角和为;
故答案为:360;
(2)①证明:∵,是四边形,
∴,
∵,
∴;
②.理由如下,
假设和交于点H,如图,
由(1)可知:,
∵平分,平分,
∴,
∵,
∴,
∵,,
∴,
∴,
即.
19.(1)解:①∵是△ABC的外角,
∴,
∴,
∵平分,平分,
∴,,
∴,
当得,当得;
故答案为:,;
②,理由如下:
∵是△ABC的外角,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴;
(2)∵,,,
∴,
∵是△BCF的外角,
∴,
∴,
∵平分,平分,
∴,,
∴
,
∴,
故答案为:;
(3)如图,延长到G,延长,交于点H,
∴,,
∵平分,平分,
∴平分,平分,
由(1)得,,
在中,,,
∴,
∴,
故答案为:;
20.(1)解:①四边形是对补四边形,,
.
故答案为:;
②证明:,
又四边形是互补四边形,
,
分别平分,
,
,
,
在中,
,
,
;
(2)解:四边形是对补四边形
理由:是的外角,
,
又,
,
,
,
,
在中,,
,
又,
,
分别平分,
,
,
四边形是对补四边形.
(3)解:第一种答案:
四边形是对补四边形,
,
为角平分线,
,
四边形内角和为,
在四边形中,
即,
,
,
即;
第二种答案:
四边形是对补四边形,
,
为角平分线,
,
在中,,
在△CDF中,,
,
即;
第三种答案:
四边形是对补四边形,
,
为角平分线,
,
在中,外角,
在中,,
即.
21.(1)解:.理由如下:
、分别平分和,
,
,
,
,
,
即;
(2)解:.理由如下:
、分别平分和,
,
,
,
,
,
即;
(3)解:.理由如下:
六边形的内角和为:,
、分别平分和,
,
,
,
,
,
,
即.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,是四边形的对角线,且四边形的内角和为,与的内角和相加为n,则( )
A. B. C. D.无法比较m,n大小关系
2.如图,直线,正五边形的边在直线上,顶点在直线上,过点作正五边形的对称轴分别交,,于点,,,则的度数为( )
A. B. C. D.
3. 是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A. B. C. D.
4.郯城县银杏叶以其高品质著称,得益于当地得天独厚的地理环境与悠久的银杏栽培传统.叶片富含有效成分,广泛应用于银杏叶茶、提取物等医药与保健品领域,享有较高声誉,深受国内外市场青睐.如图,被银杏树叶遮掩的部分是一个正边形,若直线所夹锐角为,则的值是( )
A.5 B.6 C.8 D.10
5.一个正五边形和一个正六边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则( )
A. B. C. D.
6.已知凸边形有条对角线,正边形每个内角是,则边数为的多边形的内角和是( )
A. B. C. D.
7.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美,图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则的度数是( )
A. B. C. D.
8.如图1,中华黄河楼,其内设黄河中国历史文化展览馆、黄河宁夏历史文化展览馆、黄河印象展览馆、黄河文化演艺厅等.是全方位展示黄河五千年灿烂文明的博物馆、黄河文化汇宁夏的重要载体和西部乃至全国的知名旅游景点.是宁夏黄河金岸的点晴之笔和标志性的景观工程之一,如图2是黄河楼台基底层正多边形的部分示意图,其外角为,则该正多边形是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
9.如图,,的角平分线的反向延长线和的角平分线交于点,,则( )
A. B. C. D.
二、填空题
10.如图,直线与正五边形两边交于O、Q两点,则的度数为 .
11.如图,是四边形的外角,若,则 .
12.如图是由正方形和正五边形叠放在一起形成的图形,点是边的中点,则的度数为 .
13.如图是某校数学兴趣小组活动室墙壁上的一幅图案的一部分,它是由边长相等的正方形、正三角形和正n()边形密铺(无空隙、不重叠的拼接)而成,则该正n边形一个内角的度数为 °.
14.某市举行了一次无人机表演大赛,参赛者勇勇让自己的微型无人机上升到一定高度时,开始按照如图所示的程序框图在空中完成表演,从开始表演到结束表演,勇勇的无人机飞行的总路程是 米.
三、解答题
15.规定:有一对相对的角互补的四边形叫做智慧四边形.例如,在四边形中,若或,则四边形是智慧四边形.
(1)如图1,已知四边形是智慧四边形,其中三个内角、、的比是,则的度数为______.
(2)如图2,D为△ABC内一点,且,△ABC的两个外角、的角平分线交于点E,判断四边形是否为智慧四边形,并说明理由.
16.已知:多边形的外角和的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图①,,BM与DN交于点P,求的度数;
②如图②,猜测当和满足什么数量关系时,,并证明你的猜想.
(2)如图③,若多边形是五边形ABCDG,已知,BM与DN交于点P,求的度数.
17.探究一:
已知:如图(1),在中,分别平分和,试探究与的数量关系.并说明理由.
探究二:
若将改为任意四边形呢?
已知:如图(2),在四边形中,分别平分和,请你利用上述结论探究与的数量关系,并说明理由.
探究三:若将上题中的四边形改为六边形如图(3)所示,请你直接写出与的数量关系.
18.如图1,图2,在四边形中,是四边形的一个外角.
(1)四边形的外角和为________度;
(2)如图1,图2,已知.
①如图1,求证:;
②如图2,若平分,交于点G,平分,且与相交于点F,试判断与之间的位置关系,并说明理由.
19.小东在学习中遇到这样一个问题:如图1,△ABC中,平分,平分外角.猜想与的数量关系.
(1)小东阅读题目后,没有发现数量关系与解题思路,于是尝试代入的值求的值,
①如果,则的度数为_____;如果,则的度数为_____.
②请猜想与的数量关系,并说明理由.
(2)小东继续探究,如图2,在四边形中,平分,且与四边形的外角的平分线交于点.若,,则的度数为_____.
(3)小东又思考,改变,的大小,如图3,在四边形中,四边形的内角的角平分线所在的直线与外角的角平分线所在的直线相交于点,若,,则可表示为_____.(请用含α、β的表达式表示)
20.定义:有一组对角互补的四边形叫做对补四边形.
(1)已知四边形是对补四边形.
①若,则 .
②如图①,的平分线分别与相交于点E、F,求证:;
(2)如图②,在四边形中,对角线,交于点E,且平分,,平分,与交于点F,且于点G,则四边形是对补四边形吗?请说明理由;
(3)已知四边形是对补四边形,其三个顶点A,B,D如图③所示,连接,.若平分,平分,且直线,交于点O(与点C不重合),请直接写出与之间的数量关系.
21.小亮学习了“多边形及其内角和”后,对几何学习产生了浓厚的兴趣,三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系.
【探究发现】
(1)如图①,在中,、分别平分和,试探究与的数量关系.并说明理由.
【拓展延伸】
(2)如图②,在四边形中,分别平分和,请你探究与之间的数量关系,并说明理由.
【类比迁移】
(3)若将(2)中的四边形改为六边形,如图③,请你探究与之间的数量关系,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《多边形及其内角和》专项练习题》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 B A A A D B B D C
10./144度
11.
12./度
13.150
15.(1)
(2)四边形为智慧四边形,理由见解析
16.(1)①∵,
∴在四边形ABCD中,,
,
∵多边形的外角和的平分线分别为BM,DN,
∴,
;
②当时,,
证明:如图,连接,
∵,
,
,
即,
,
,
∴;
(2)如图,延长交于点Q,
∵,,
,
∴,
∵平分,平分,
,
,
,
.
17.解:探究一:,理由如下:
解:∵分别平分和,
∴,
∴,
,
,
,
;
探究二:,理由如下:
∵分别平分和,
∴,
∴,
,
,
,
;
探究三:六边形的内角和为:,
∵分别平分和,
∴,
∴,
,
,
,
,
即.
18.(1)解:四边形的外角和为;
故答案为:360;
(2)①证明:∵,是四边形,
∴,
∵,
∴;
②.理由如下,
假设和交于点H,如图,
由(1)可知:,
∵平分,平分,
∴,
∵,
∴,
∵,,
∴,
∴,
即.
19.(1)解:①∵是△ABC的外角,
∴,
∴,
∵平分,平分,
∴,,
∴,
当得,当得;
故答案为:,;
②,理由如下:
∵是△ABC的外角,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴;
(2)∵,,,
∴,
∵是△BCF的外角,
∴,
∴,
∵平分,平分,
∴,,
∴
,
∴,
故答案为:;
(3)如图,延长到G,延长,交于点H,
∴,,
∵平分,平分,
∴平分,平分,
由(1)得,,
在中,,,
∴,
∴,
故答案为:;
20.(1)解:①四边形是对补四边形,,
.
故答案为:;
②证明:,
又四边形是互补四边形,
,
分别平分,
,
,
,
在中,
,
,
;
(2)解:四边形是对补四边形
理由:是的外角,
,
又,
,
,
,
,
在中,,
,
又,
,
分别平分,
,
,
四边形是对补四边形.
(3)解:第一种答案:
四边形是对补四边形,
,
为角平分线,
,
四边形内角和为,
在四边形中,
即,
,
,
即;
第二种答案:
四边形是对补四边形,
,
为角平分线,
,
在中,,
在△CDF中,,
,
即;
第三种答案:
四边形是对补四边形,
,
为角平分线,
,
在中,外角,
在中,,
即.
21.(1)解:.理由如下:
、分别平分和,
,
,
,
,
,
即;
(2)解:.理由如下:
、分别平分和,
,
,
,
,
,
即;
(3)解:.理由如下:
六边形的内角和为:,
、分别平分和,
,
,
,
,
,
,
即.
答案第1页,共2页
答案第1页,共2页
同课章节目录
