第4单元比例能力提升卷(含解析)-2024-2025学年数学六年级下册苏教版
文档属性
| 名称 | 第4单元比例能力提升卷(含解析)-2024-2025学年数学六年级下册苏教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 407.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 15:04:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4单元比例能力提升卷-2024-2025学年数学六年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面与∶能组成比例的是( )。
A.2∶3 B.3∶2 C.1∶6 D.0.03∶0.2
2.把a=3b(a、b均不为0)写成比例式可能是( )。
A.=3 B.= C.= D.=
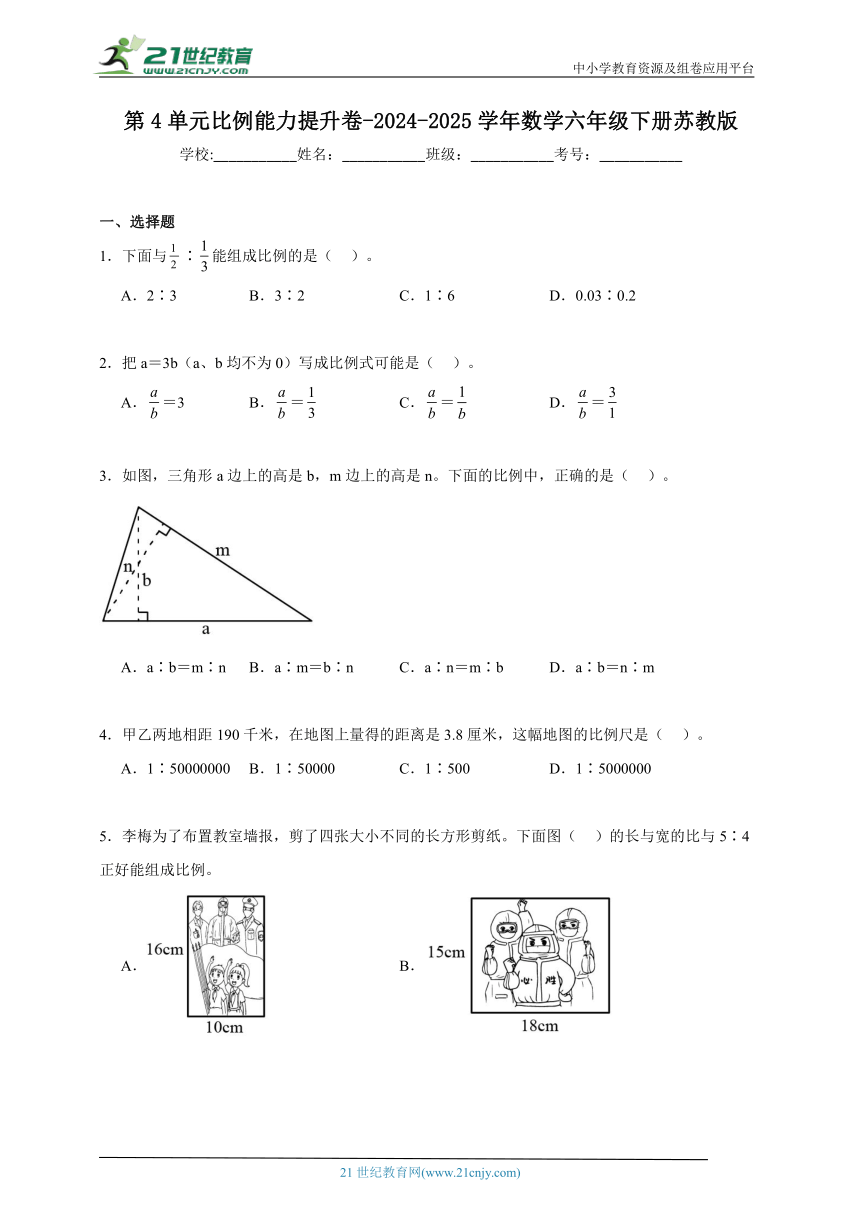
3.如图,三角形a边上的高是b,m边上的高是n。下面的比例中,正确的是( )。
A.a∶b=m∶n B.a∶m=b∶n C.a∶n=m∶b D.a∶b=n∶m
4.甲乙两地相距190千米,在地图上量得的距离是3.8厘米,这幅地图的比例尺是( )。
A.1∶50000000 B.1∶50000 C.1∶500 D.1∶5000000
5.李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。下面图( )的长与宽的比与5∶4正好能组成比例。
A. B.
C. D.
6.在中,扩大10倍,要使比例成立,下列说法正确的是( )。
A.扩大10倍 B.扩大10倍
C.缩小10倍 D.和同时缩小10倍
二、填空题
7.如果x与y互为倒数,且那么24n=( )。
8.如果(a、b都不等于0),那么:a∶b=( )(填最简整数比),( )。
9.一种精密零件长2.5毫米,画在图纸上长25厘米,这幅图纸的比例尺是( )。
10.为支援上海抗疫,本地“爱心”医疗队从上午10时以100千米/时的速度开车驶往上海,出发前他们从一幅比例尺为1∶3000000的地图上量得本地到上海的距离为11厘米,则本地到上海的实际距离为( )千米,预计到达的时间为( )。
11.用4、3、15和x组成比例,x最小是( ),最大是( )。
12.一个直角三角形的三条角边分别是5厘米、4厘米、3厘米,按3∶1的比放大后得到的图形的面积是( )平方厘米。
三、判断题
13.交换比例的两个外项(外项不为0),比例仍然成立。( )
14.在7∶x=2∶7中,x=2。( )
15.我国的国家基本比例尺地图的比例尺共有11种。( )
16.把一个圆按1∶3的比缩小后,周长是原来的,面积是原来的。( )
17.放大或缩小后的图形与原图形相比较,形状变了,但大小没变。( )
四、计算题
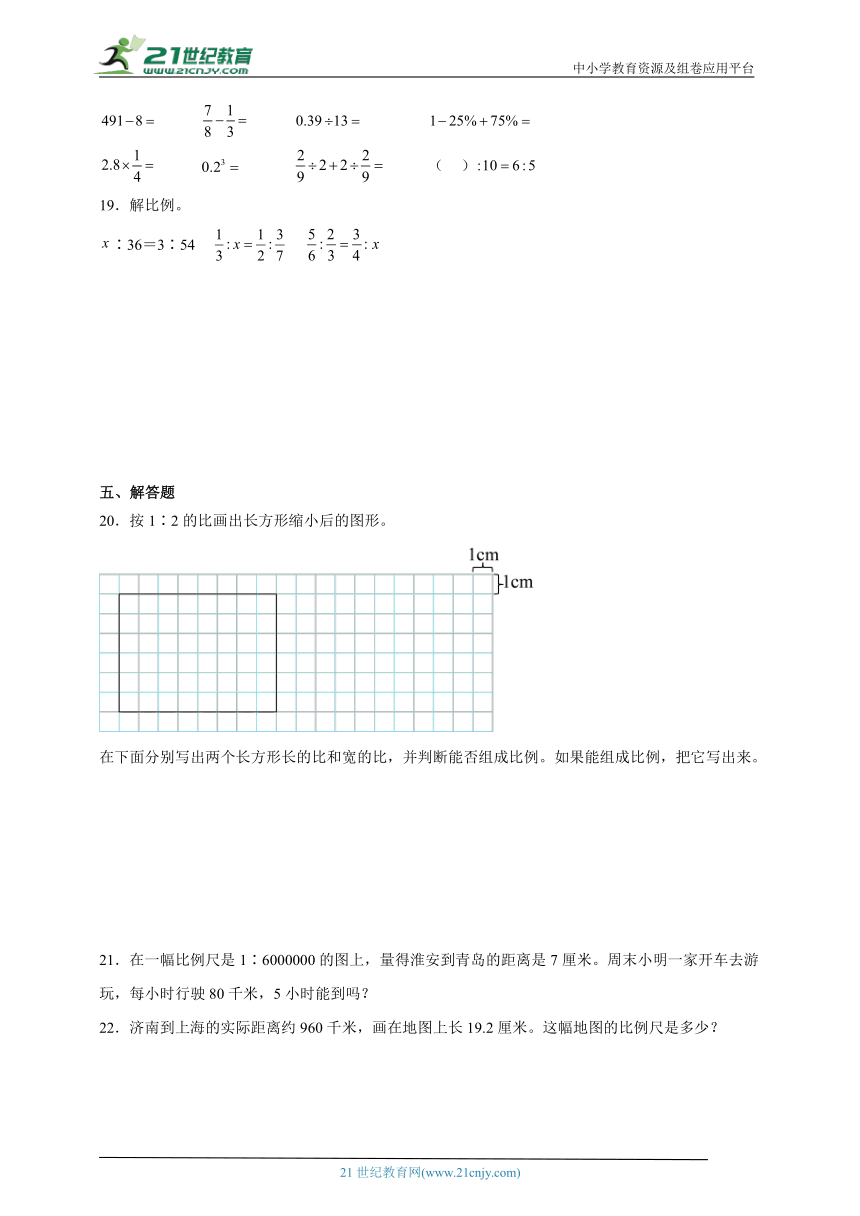
18.直接写出得数。
( )
19.解比例。
∶36=3∶54
五、解答题
20.按1∶2的比画出长方形缩小后的图形。
在下面分别写出两个长方形长的比和宽的比,并判断能否组成比例。如果能组成比例,把它写出来。
21.在一幅比例尺是1∶6000000的图上,量得淮安到青岛的距离是7厘米。周末小明一家开车去游玩,每小时行驶80千米,5小时能到吗?
22.济南到上海的实际距离约960千米,画在地图上长19.2厘米。这幅地图的比例尺是多少?
23.用黄铜和黄金制成一种合金。黄铜与黄金的质量比是5∶2,现在有黄金40克,要制成这种合金,需要黄铜多少克?(列比例解答)
24.在一幅比例尺为的地图上,甲、乙两地相距5cm,A、B两车分别从甲、乙两地同时出发,已知A、B两车的速度之比为2∶3,两车相遇时,乙车距离甲地有多远?
25.按要求画一画。
(1)把图①向下平移4格。
(2)在方格里画出图②的另一半,使它成为轴对称图形。
(3)图③中点O的位置用数对表示是( ),把图③绕点O逆时针旋转90°。画出旋转后的图形。
(4)按3∶2的比在方格纸上画出图④放大后的图形,并画出它的一条对称轴。
《第4单元比例能力提升卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 B D C D D B
1.B
【分析】表示两个比相等的式子,叫做比例;据此求出各项中的比值,比值相等的即可组成比例。
【详解】∶
=×3
=
A.2∶3
=2÷3
=
≠,所以∶和2∶3不能组成比例。
B.3∶2
=3÷2
=
=,所以∶和3∶2能组成比例。
C.1∶6
=1÷6
=
≠,所以∶和1∶6不能组成比例。
D.0.03∶0.2
=0.03÷0.2
=
≠,所以∶和0.03∶0.2不能组成比例。
故答案为:B
2.D
【分析】根据比例的基本性质,分别将各选项中的比例写成两内项积=两外项积的形式,是a=3b的即可。
【详解】A.=3,不是个比例式,排除;
B.=,根据比例的基本性质,可得3a=b,排除;
C.=,根据比例的基本性质,可得ab=b,排除;
D.=,根据比例的基本性质,可得a=3b,符合。
把a=3b(a、b均不为0)写成比例式可能是=。
故答案为:D
3.C
【分析】根据三角形面积公式:面积=底×高÷2;三角形的面积=ab÷2=mn÷2;即ab=mn,再根据比例的基本性质:比例的两个内项之积等于两个外项之积,逐项分析,据此解答。
【详解】A.a∶b=m∶n;an=bm;不符合题意;
B.a∶m=b∶n;an=bm,不符合题意;
C.a∶n=m∶b;ab=mn,符合题意;
D.a∶b=n∶m;am=bn,不符合题意。
三角形a边上的高是b,m边上的高是n。下面的比例中,正确的是a∶n=m∶b。
故答案为:C
【点睛】熟练掌握三角形面积公式以及比例的基本性质是解答本题的关键。
4.D
【分析】图上距离与实际距离的比,叫做这幅图的比例尺;根据1千米=100000厘米,所以190千米=19000000厘米,再用3.8比19000000,最后根据比的基本性质:比的前项和比的后项同时乘或除以同一个不为0的数,比值的大小仍然不变,把原式化简成最简整数比即可。
【详解】由分析可知:
190千米=19000000厘米
3.8∶19000000
=(3.8×10)∶(19000000×10)
=38∶190000000
=(38÷38)∶(190000000÷38)
=1∶5000000
所以这幅地图的比例尺是1∶5000000。
故答案为:D
【点睛】本题考查求比例尺,理解比例尺的意义是关键。
5.D
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此逐项分析,进行解答。
【详解】A。,16∶10和5∶4;
10×5=50;16×4=64
50≠64;16∶10与5∶4不能组成比例,不符合题意;
B.,18∶15和5∶4;
18×4=72;15×5=75
72≠75;18∶15与5∶4不能组成比例,不符合题意;
C.;12∶9和5∶4;
12×4=48,9×5=45;
48≠45;12∶9与5∶4不能组成比例,不符合题意;
D.;15∶12和5∶4;
15×4=60;12×5=60
60=60;15∶12和5∶4能组成比例,符合题意。
李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。的长与宽的比与5∶4正好能组成比例。
故答案为:D
【点睛】熟练掌握比例的基本性质是解答本题的关键。
6.B
【分析】根据比例的性质:两个外项之积等于两个内项之积;因为a∶b=c∶d,所以ad=bc;若c扩大10倍,根据积的变化规律,使等式成立的条件有:a扩大10倍或d扩大10倍,据此解答。
【详解】根据分析可知,在a∶b=c∶d中,c扩大10倍,要使比例成立,下列说法正确的是d扩大10倍。
故答案为:B
【点睛】熟练掌握比例的基本性质和积的变化规律是解答本题的关键。
7.8
【分析】根据倒数的意义:乘积是1的两个数互为倒数;x与y互为倒数,则xy=1;根据比例的基本性质:比例的两个内项之积等于两个外项之积;把=化为3n=xy,因为xy=1,所以3n=1,据此求出n的值,再把n的值代入算式24n,即可解答。
【详解】xy=1
=
3n=xy
3n=1
n=1÷3
n=
24n=24×=8
如果x与y互为倒数,且那么24n=8。
8. 21∶20
【分析】根据比例基本性质,比例基本性质就是两内项之积等于两外项之积。由可得5a×4=3b×7,即20a=21b,所以a∶b=21∶20。又因为20a=21b,所以=。
【详解】(1)已知,则 a∶b=∶=(×28)∶(×28)= 21∶20
a∶b= 21∶20
(2)由可得==×=
=
9.100∶1
【分析】根据比例尺=图上距离∶实际距离,已知精密零件长2.5毫米,画在图纸上长25厘米,统一单位后,把数据代入即可求出这幅图纸的比例尺。据此解答即可。
【详解】25厘米=250毫米
250∶2.5=100∶1
所以,这幅图纸的比例尺是100∶1。
10. 330 13时18分
【分析】根据题意,图上距离÷比例尺=实际距离,算出路程,再除以速度,求出所用时间,开始时刻+经过时间=到达时间,据此解答。
【详解】11÷=33000000(厘米)
33000000厘米=330千米
330÷100=3.3(小时)
3.3小时=3小时18分
10时+3小时18分钟=13时18分。
11. 0.8 20
【分析】依据比例的基本性质,即两内项之积等于两外项之积,先求出两个最大数的积,即可求得x的最大值,再求两个最小数的积,即可求得x的最小值。
【详解】15×4÷3
=60÷3
=20
4×3÷15
=12÷15
=0.8
x最大是20,x最小是0.8。
12.54
【分析】把一个直角三角形按3∶1的比放大,即把该直角三角形的底和高(两条直角边)分别扩大到原来的3倍,再根据三角形面积公式:面积=底×高÷2,将数据代入求值即可。
【详解】由分析可得:
4×3=12(厘米)
3×3=9(厘米)
12×9÷2
=108÷2
=54(平方厘米)
综上所述:一个直角三角形的三条角边分别是5厘米、4厘米、3厘米,按3∶1的比放大后得到的图形的面积是54平方厘米。
13.√
【分析】依据比例的基本性质,即两个内项之积等于两个外项之积,即可进行判断。
【详解】在一个比例中,两个外项交换位置后,两个内项之积仍然等于两个外项之积,所以仍是比例,例如:2∶3=4∶6,6∶3=4∶2。
故答案为:√
【点睛】此题主要考查比例的基本性质,解答时可以举例证明。
14.×
【分析】根据比例的基本性质,将比例转化为方程,再根据等式的性质2解方程即可判断。
【详解】7∶x=2∶7
解:2x=7×7
x=49÷2
x=24.5
故答案为:×
【点睛】本题主要考查解比例的方法。
15.√
【解析】我国的国家基本比例尺地图的比例尺有如下几种,1∶500、1∶1000、1∶2000、1∶5000、1∶10000、1∶25000、1∶50000、1∶100000、1∶250000、1∶500000、1∶1000000,总共11种。
【详解】国的国家基本比例尺地图的比例尺共有11种;
题干阐述正确,答案为:√。
【点睛】本题主要考查学生的知识积累,对于数学中的一些常识问题要做到非常熟悉。
16.×
【分析】假设圆的半径为r,则按1∶3的比缩小后,其半径为 r,据此表示出缩小后圆的周长和面积,与原来比较即可。
【详解】假设圆的半径为r,则按1∶3的比缩小后,周长为2π(r)= πr;是原来的( πr)÷(2πr)=。
面积为π(r)2= πr2,是原来的( πr2)÷(πr2)=。
故答案为:×
【点睛】此题考查了图形的放缩以及圆的周长、面积的综合应用,注意灵活运用公式解答。
17.×
【分析】图形的放大或缩小,只是对应边的放大或缩小,图形的形状不变,大小发生了变化,据此判断。
【详解】由分析可知,放大或缩小后的图形与原图形相比较,形状不变,但大小变了。原题说法错误。
故答案为×
【点睛】此题考查了图形的放大和缩小,属于基础类题目。
18.483;;0.03;1.5;
0.7;0.008;9;12
【详解】略
19.;;
【分析】(1)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以54,计算即可得解;
(2)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解;
(3)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解。
【详解】∶36=3∶54
解:
解:
解:
20.图见详解
8∶4=6∶3
【分析】按1∶2的比例画出长方形缩小后的图形,就是把原来长方形的长和宽分别缩小到原来的,求出缩小后长方形的长和宽,画出缩小后的长方形。
根据比的意义,分别求出原来长方形长与缩小后长方形长的比;原来长方形宽与缩小后长方形宽的比;再分别求出它们的比值,再根据比例的意义判断能否组成比例,进而解答。
【详解】原来长方形的长:1×8=8(厘米),原来长方形的宽:1×6=(厘米);
缩小后长方形的长时:8×=4(厘米),缩小后长方形的宽:6×=3(厘米)。
如图:
(位置不唯一)
原来长方形长∶缩小后长方形长=8∶4
=(8÷4)∶(4÷4)
=2∶1
原来长方形宽∶缩小后长方形宽=6∶3
=(6÷3)∶(3÷3)
=2∶1
2∶1
=2÷1
=2
2∶1
=2÷1
=2
2=2;原来长方形的长∶缩小后长方形的长与原来长方形的宽∶缩小后长方形的宽能组成比例。
8∶4=6∶3
21.不能到达
【分析】根据实际距离=图上距离÷比例尺,代入数据求出淮安到青岛的实际距离,再根据时间=路程÷速度,代入数据求出小明一家开车的时间,再进行比较,即可解答。
【详解】7÷
=7×6000000
=42000000(厘米)
42000000厘米=420千米
420÷80=5.25(小时)
5<5.25,5小时不能到达。
答:5小时不能到达。
【点睛】熟练掌握图上距离和实际距离的换算,以及利用速度、时间和路程三者的关系进行解答,注意单位名数的换算。
22.1∶5000000
【分析】比例尺=图上距离∶实际距离,据此先统一单位,再写出比例尺。
【详解】960千米=96000000厘米
19.2∶96000000=1∶5000000
答:这幅地图的比例尺是1∶5000000。
【点睛】掌握比例尺的意义是解题的关键。
23.100克
【分析】设需要黄铜x克,根据黄铜与黄金的质量比是5∶2列出比例求解即可。
【详解】解:设需要黄铜x克。
2x=40×5
2x÷2=200÷2
答:需要黄铜100克。
【点睛】本题主要考查比例的应用,理解比例的意义是解题的关键。
24.40千米
【分析】先用图上距离除以比例尺求出全程,再换算单位;已知A、B两车的速度之比为2∶3,则路程之比也是2∶3,要求乙车距离甲地有多远,就用全程乘即可。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
100×
=100×
=40(千米)
答:乙车距离甲地40千米。
【点睛】本题主要考查了比例尺应用题及相遇问题的灵活应用。
25.作图见详解(画对称轴答案不唯一);(3)16,3
【分析】(1)根据平移的特征,把图①的各顶点分别向下平移4格,依次连接即可得到平移后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左半图的关键对称点,依次连接即可。
(3)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对表示出点O的位置;根据旋转的特征,图③绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(4)图形④是边长为2格的正方形,根据图形放大的意义,按3∶2放大后图形是边长为3格的正方形。正方形有4条对称轴,即过对边中点的直线、对角线所在的直线。
【详解】
(3)图③中点O的位置用数对表示是(16,3)。
【点睛】此题考查的知识点:作平移后的图形、作旋转一定度数后的图形、作轴对称图形、图形的放大与缩小、确定轴对称图形对称轴的条数及位置、数对与位置。要牢固掌握相关知识并熟练运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4单元比例能力提升卷-2024-2025学年数学六年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面与∶能组成比例的是( )。
A.2∶3 B.3∶2 C.1∶6 D.0.03∶0.2
2.把a=3b(a、b均不为0)写成比例式可能是( )。
A.=3 B.= C.= D.=
3.如图,三角形a边上的高是b,m边上的高是n。下面的比例中,正确的是( )。
A.a∶b=m∶n B.a∶m=b∶n C.a∶n=m∶b D.a∶b=n∶m
4.甲乙两地相距190千米,在地图上量得的距离是3.8厘米,这幅地图的比例尺是( )。
A.1∶50000000 B.1∶50000 C.1∶500 D.1∶5000000
5.李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。下面图( )的长与宽的比与5∶4正好能组成比例。
A. B.
C. D.
6.在中,扩大10倍,要使比例成立,下列说法正确的是( )。
A.扩大10倍 B.扩大10倍
C.缩小10倍 D.和同时缩小10倍
二、填空题
7.如果x与y互为倒数,且那么24n=( )。
8.如果(a、b都不等于0),那么:a∶b=( )(填最简整数比),( )。
9.一种精密零件长2.5毫米,画在图纸上长25厘米,这幅图纸的比例尺是( )。
10.为支援上海抗疫,本地“爱心”医疗队从上午10时以100千米/时的速度开车驶往上海,出发前他们从一幅比例尺为1∶3000000的地图上量得本地到上海的距离为11厘米,则本地到上海的实际距离为( )千米,预计到达的时间为( )。
11.用4、3、15和x组成比例,x最小是( ),最大是( )。
12.一个直角三角形的三条角边分别是5厘米、4厘米、3厘米,按3∶1的比放大后得到的图形的面积是( )平方厘米。
三、判断题
13.交换比例的两个外项(外项不为0),比例仍然成立。( )
14.在7∶x=2∶7中,x=2。( )
15.我国的国家基本比例尺地图的比例尺共有11种。( )
16.把一个圆按1∶3的比缩小后,周长是原来的,面积是原来的。( )
17.放大或缩小后的图形与原图形相比较,形状变了,但大小没变。( )
四、计算题
18.直接写出得数。
( )
19.解比例。
∶36=3∶54
五、解答题
20.按1∶2的比画出长方形缩小后的图形。
在下面分别写出两个长方形长的比和宽的比,并判断能否组成比例。如果能组成比例,把它写出来。
21.在一幅比例尺是1∶6000000的图上,量得淮安到青岛的距离是7厘米。周末小明一家开车去游玩,每小时行驶80千米,5小时能到吗?
22.济南到上海的实际距离约960千米,画在地图上长19.2厘米。这幅地图的比例尺是多少?
23.用黄铜和黄金制成一种合金。黄铜与黄金的质量比是5∶2,现在有黄金40克,要制成这种合金,需要黄铜多少克?(列比例解答)
24.在一幅比例尺为的地图上,甲、乙两地相距5cm,A、B两车分别从甲、乙两地同时出发,已知A、B两车的速度之比为2∶3,两车相遇时,乙车距离甲地有多远?
25.按要求画一画。
(1)把图①向下平移4格。
(2)在方格里画出图②的另一半,使它成为轴对称图形。
(3)图③中点O的位置用数对表示是( ),把图③绕点O逆时针旋转90°。画出旋转后的图形。
(4)按3∶2的比在方格纸上画出图④放大后的图形,并画出它的一条对称轴。
《第4单元比例能力提升卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 B D C D D B
1.B
【分析】表示两个比相等的式子,叫做比例;据此求出各项中的比值,比值相等的即可组成比例。
【详解】∶
=×3
=
A.2∶3
=2÷3
=
≠,所以∶和2∶3不能组成比例。
B.3∶2
=3÷2
=
=,所以∶和3∶2能组成比例。
C.1∶6
=1÷6
=
≠,所以∶和1∶6不能组成比例。
D.0.03∶0.2
=0.03÷0.2
=
≠,所以∶和0.03∶0.2不能组成比例。
故答案为:B
2.D
【分析】根据比例的基本性质,分别将各选项中的比例写成两内项积=两外项积的形式,是a=3b的即可。
【详解】A.=3,不是个比例式,排除;
B.=,根据比例的基本性质,可得3a=b,排除;
C.=,根据比例的基本性质,可得ab=b,排除;
D.=,根据比例的基本性质,可得a=3b,符合。
把a=3b(a、b均不为0)写成比例式可能是=。
故答案为:D
3.C
【分析】根据三角形面积公式:面积=底×高÷2;三角形的面积=ab÷2=mn÷2;即ab=mn,再根据比例的基本性质:比例的两个内项之积等于两个外项之积,逐项分析,据此解答。
【详解】A.a∶b=m∶n;an=bm;不符合题意;
B.a∶m=b∶n;an=bm,不符合题意;
C.a∶n=m∶b;ab=mn,符合题意;
D.a∶b=n∶m;am=bn,不符合题意。
三角形a边上的高是b,m边上的高是n。下面的比例中,正确的是a∶n=m∶b。
故答案为:C
【点睛】熟练掌握三角形面积公式以及比例的基本性质是解答本题的关键。
4.D
【分析】图上距离与实际距离的比,叫做这幅图的比例尺;根据1千米=100000厘米,所以190千米=19000000厘米,再用3.8比19000000,最后根据比的基本性质:比的前项和比的后项同时乘或除以同一个不为0的数,比值的大小仍然不变,把原式化简成最简整数比即可。
【详解】由分析可知:
190千米=19000000厘米
3.8∶19000000
=(3.8×10)∶(19000000×10)
=38∶190000000
=(38÷38)∶(190000000÷38)
=1∶5000000
所以这幅地图的比例尺是1∶5000000。
故答案为:D
【点睛】本题考查求比例尺,理解比例尺的意义是关键。
5.D
【分析】根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此逐项分析,进行解答。
【详解】A。,16∶10和5∶4;
10×5=50;16×4=64
50≠64;16∶10与5∶4不能组成比例,不符合题意;
B.,18∶15和5∶4;
18×4=72;15×5=75
72≠75;18∶15与5∶4不能组成比例,不符合题意;
C.;12∶9和5∶4;
12×4=48,9×5=45;
48≠45;12∶9与5∶4不能组成比例,不符合题意;
D.;15∶12和5∶4;
15×4=60;12×5=60
60=60;15∶12和5∶4能组成比例,符合题意。
李梅为了布置教室墙报,剪了四张大小不同的长方形剪纸。的长与宽的比与5∶4正好能组成比例。
故答案为:D
【点睛】熟练掌握比例的基本性质是解答本题的关键。
6.B
【分析】根据比例的性质:两个外项之积等于两个内项之积;因为a∶b=c∶d,所以ad=bc;若c扩大10倍,根据积的变化规律,使等式成立的条件有:a扩大10倍或d扩大10倍,据此解答。
【详解】根据分析可知,在a∶b=c∶d中,c扩大10倍,要使比例成立,下列说法正确的是d扩大10倍。
故答案为:B
【点睛】熟练掌握比例的基本性质和积的变化规律是解答本题的关键。
7.8
【分析】根据倒数的意义:乘积是1的两个数互为倒数;x与y互为倒数,则xy=1;根据比例的基本性质:比例的两个内项之积等于两个外项之积;把=化为3n=xy,因为xy=1,所以3n=1,据此求出n的值,再把n的值代入算式24n,即可解答。
【详解】xy=1
=
3n=xy
3n=1
n=1÷3
n=
24n=24×=8
如果x与y互为倒数,且那么24n=8。
8. 21∶20
【分析】根据比例基本性质,比例基本性质就是两内项之积等于两外项之积。由可得5a×4=3b×7,即20a=21b,所以a∶b=21∶20。又因为20a=21b,所以=。
【详解】(1)已知,则 a∶b=∶=(×28)∶(×28)= 21∶20
a∶b= 21∶20
(2)由可得==×=
=
9.100∶1
【分析】根据比例尺=图上距离∶实际距离,已知精密零件长2.5毫米,画在图纸上长25厘米,统一单位后,把数据代入即可求出这幅图纸的比例尺。据此解答即可。
【详解】25厘米=250毫米
250∶2.5=100∶1
所以,这幅图纸的比例尺是100∶1。
10. 330 13时18分
【分析】根据题意,图上距离÷比例尺=实际距离,算出路程,再除以速度,求出所用时间,开始时刻+经过时间=到达时间,据此解答。
【详解】11÷=33000000(厘米)
33000000厘米=330千米
330÷100=3.3(小时)
3.3小时=3小时18分
10时+3小时18分钟=13时18分。
11. 0.8 20
【分析】依据比例的基本性质,即两内项之积等于两外项之积,先求出两个最大数的积,即可求得x的最大值,再求两个最小数的积,即可求得x的最小值。
【详解】15×4÷3
=60÷3
=20
4×3÷15
=12÷15
=0.8
x最大是20,x最小是0.8。
12.54
【分析】把一个直角三角形按3∶1的比放大,即把该直角三角形的底和高(两条直角边)分别扩大到原来的3倍,再根据三角形面积公式:面积=底×高÷2,将数据代入求值即可。
【详解】由分析可得:
4×3=12(厘米)
3×3=9(厘米)
12×9÷2
=108÷2
=54(平方厘米)
综上所述:一个直角三角形的三条角边分别是5厘米、4厘米、3厘米,按3∶1的比放大后得到的图形的面积是54平方厘米。
13.√
【分析】依据比例的基本性质,即两个内项之积等于两个外项之积,即可进行判断。
【详解】在一个比例中,两个外项交换位置后,两个内项之积仍然等于两个外项之积,所以仍是比例,例如:2∶3=4∶6,6∶3=4∶2。
故答案为:√
【点睛】此题主要考查比例的基本性质,解答时可以举例证明。
14.×
【分析】根据比例的基本性质,将比例转化为方程,再根据等式的性质2解方程即可判断。
【详解】7∶x=2∶7
解:2x=7×7
x=49÷2
x=24.5
故答案为:×
【点睛】本题主要考查解比例的方法。
15.√
【解析】我国的国家基本比例尺地图的比例尺有如下几种,1∶500、1∶1000、1∶2000、1∶5000、1∶10000、1∶25000、1∶50000、1∶100000、1∶250000、1∶500000、1∶1000000,总共11种。
【详解】国的国家基本比例尺地图的比例尺共有11种;
题干阐述正确,答案为:√。
【点睛】本题主要考查学生的知识积累,对于数学中的一些常识问题要做到非常熟悉。
16.×
【分析】假设圆的半径为r,则按1∶3的比缩小后,其半径为 r,据此表示出缩小后圆的周长和面积,与原来比较即可。
【详解】假设圆的半径为r,则按1∶3的比缩小后,周长为2π(r)= πr;是原来的( πr)÷(2πr)=。
面积为π(r)2= πr2,是原来的( πr2)÷(πr2)=。
故答案为:×
【点睛】此题考查了图形的放缩以及圆的周长、面积的综合应用,注意灵活运用公式解答。
17.×
【分析】图形的放大或缩小,只是对应边的放大或缩小,图形的形状不变,大小发生了变化,据此判断。
【详解】由分析可知,放大或缩小后的图形与原图形相比较,形状不变,但大小变了。原题说法错误。
故答案为×
【点睛】此题考查了图形的放大和缩小,属于基础类题目。
18.483;;0.03;1.5;
0.7;0.008;9;12
【详解】略
19.;;
【分析】(1)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以54,计算即可得解;
(2)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解;
(3)根据比例的基本性质:两内项之积等于两外项之积。把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解。
【详解】∶36=3∶54
解:
解:
解:
20.图见详解
8∶4=6∶3
【分析】按1∶2的比例画出长方形缩小后的图形,就是把原来长方形的长和宽分别缩小到原来的,求出缩小后长方形的长和宽,画出缩小后的长方形。
根据比的意义,分别求出原来长方形长与缩小后长方形长的比;原来长方形宽与缩小后长方形宽的比;再分别求出它们的比值,再根据比例的意义判断能否组成比例,进而解答。
【详解】原来长方形的长:1×8=8(厘米),原来长方形的宽:1×6=(厘米);
缩小后长方形的长时:8×=4(厘米),缩小后长方形的宽:6×=3(厘米)。
如图:
(位置不唯一)
原来长方形长∶缩小后长方形长=8∶4
=(8÷4)∶(4÷4)
=2∶1
原来长方形宽∶缩小后长方形宽=6∶3
=(6÷3)∶(3÷3)
=2∶1
2∶1
=2÷1
=2
2∶1
=2÷1
=2
2=2;原来长方形的长∶缩小后长方形的长与原来长方形的宽∶缩小后长方形的宽能组成比例。
8∶4=6∶3
21.不能到达
【分析】根据实际距离=图上距离÷比例尺,代入数据求出淮安到青岛的实际距离,再根据时间=路程÷速度,代入数据求出小明一家开车的时间,再进行比较,即可解答。
【详解】7÷
=7×6000000
=42000000(厘米)
42000000厘米=420千米
420÷80=5.25(小时)
5<5.25,5小时不能到达。
答:5小时不能到达。
【点睛】熟练掌握图上距离和实际距离的换算,以及利用速度、时间和路程三者的关系进行解答,注意单位名数的换算。
22.1∶5000000
【分析】比例尺=图上距离∶实际距离,据此先统一单位,再写出比例尺。
【详解】960千米=96000000厘米
19.2∶96000000=1∶5000000
答:这幅地图的比例尺是1∶5000000。
【点睛】掌握比例尺的意义是解题的关键。
23.100克
【分析】设需要黄铜x克,根据黄铜与黄金的质量比是5∶2列出比例求解即可。
【详解】解:设需要黄铜x克。
2x=40×5
2x÷2=200÷2
答:需要黄铜100克。
【点睛】本题主要考查比例的应用,理解比例的意义是解题的关键。
24.40千米
【分析】先用图上距离除以比例尺求出全程,再换算单位;已知A、B两车的速度之比为2∶3,则路程之比也是2∶3,要求乙车距离甲地有多远,就用全程乘即可。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
100×
=100×
=40(千米)
答:乙车距离甲地40千米。
【点睛】本题主要考查了比例尺应用题及相遇问题的灵活应用。
25.作图见详解(画对称轴答案不唯一);(3)16,3
【分析】(1)根据平移的特征,把图①的各顶点分别向下平移4格,依次连接即可得到平移后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左半图的关键对称点,依次连接即可。
(3)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对表示出点O的位置;根据旋转的特征,图③绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(4)图形④是边长为2格的正方形,根据图形放大的意义,按3∶2放大后图形是边长为3格的正方形。正方形有4条对称轴,即过对边中点的直线、对角线所在的直线。
【详解】
(3)图③中点O的位置用数对表示是(16,3)。
【点睛】此题考查的知识点:作平移后的图形、作旋转一定度数后的图形、作轴对称图形、图形的放大与缩小、确定轴对称图形对称轴的条数及位置、数对与位置。要牢固掌握相关知识并熟练运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
