第6单元正比例和反比例能力提升卷(含解析)-2024-2025学年数学六年级下册苏教版
文档属性
| 名称 | 第6单元正比例和反比例能力提升卷(含解析)-2024-2025学年数学六年级下册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 257.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例能力提升卷-2024-2025学年数学六年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.假如b=k×a,b是一定的,a、b、k均不为0,下列说法正确的是( )。
A.a和k成正比例关系 B.k和a成反比例关系
C.a和k不成比例 D.无法判断
2.下列各项中,两种量成反比例关系的是( )。
A.车轮周长一定,车轮行驶的路程和转数。
B.一(5)班今天的出勤人数和未出勤人数。
C.工作时间一定,加工零件总数和加工每个零件的时间。
D.圆柱体的高一定,它的底面积和体积。
3.各种长方形,考虑长和宽的关系,下边的图像相当于下面的哪种情况,( )。
A.长一定的长方形 B.周长一定的长方形
C.面积一定的长方形 D.形状一定的长方形
4.下列各选项的两个量,不成正比例的是( )。
A.圆的半径与直径 B.圆的半径与周长
C.圆的半径与面积 D.圆的直径与周长
5.10枚硬币摞在一起高1.9厘米,照这样推算,一百万枚1元硬币摞在一起大约有多高( )。
A.190米 B.1900米 C.19千米 D.190千米
6.下表中如果X和Y成反比例,空缺处填( );如果X和Y成正比例,空缺处填( )。
X 8 10
Y 12
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
二、填空题
7.下面各题中的两种量,成正比例的画“”,成反比例的画“”,不成比例的画“×”。
(1)自来水管内水的流速一定,放水的时间和放水量( )。
(2)圆的半径和面积( )。
(3)仓库存粮的总质量一定,运出的质量和剩下的质量( )。
(4)已知xy=5,x和y( )。
8.
图中的曲线表示( )比例关系。点A表示单价是( )元,能买( )本;点B表示单价是( )元,能买( )本。
9.一辆汽车从甲地开往乙地,如果每小时行70千米,那么5小时到达;如果每小时行87.5千米,那么4小时到达。这辆汽车第一次行驶的速度和时间的积是( )千米,第二次行驶的速度和时间的积是( )千米。( )一定,( )和( )成( )比例。
10.小明在数学实践课中,利用硬纸条做了一个平衡支架开展数学实验。如果在支架左侧第4个孔挂3颗珠,右侧第3个孔应挂( )颗珠才能保持平衡。
11.如果,那么和成( )比例;如果∶3=10∶,那么和成( )比例。
12.六年级同学做广播操,每行站15人,可以站12行。如果每行站18人,能站多少行?此题中,每行站的人数和能站多少行成( )比例关系。
三、判断题
13.正方形的边长和它的周长不成比例。( )
14.每块地砖的面积一定,地砖的块数和铺地面积成正比例。( )
15.车轮前进的距离一定,车轮的周长和转动的周数成反比例。( )
16.加工一批零件,加工效率和加工时间成反比例。( )
17.绳子的长度一定,剪去的绳子和剩下的绳子成正比例。( )
四、解答题
18.自来水公司修建自来水管道,用8米长的新管更换原来5米长的旧管。现在有240根新管,可更换旧管多少根?
19.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
20.学校会议室用方砖铺地,用面积16平方分米的方砖,需要150块,如果改用边长是5分米的方砖要用多少块?(用比例解)
21.甲、乙、丙三人进行100米短跑赛。甲到终点时,乙跑了80米,丙离终点30米。那么,当乙到终点时,丙离终点还有多远?(用比例解)
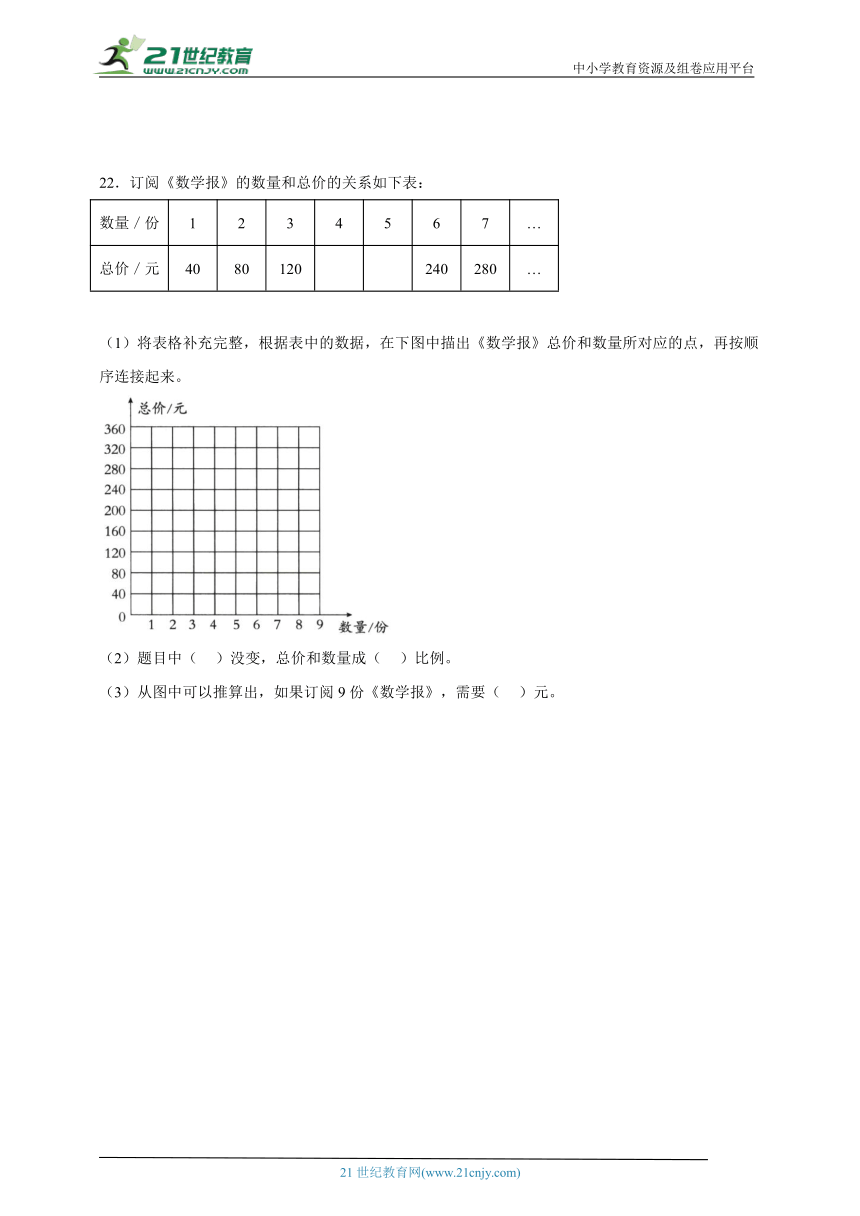
22.订阅《数学报》的数量和总价的关系如下表:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 240 280 …
(1)将表格补充完整,根据表中的数据,在下图中描出《数学报》总价和数量所对应的点,再按顺序连接起来。
(2)题目中( )没变,总价和数量成( )比例。
(3)从图中可以推算出,如果订阅9份《数学报》,需要( )元。
《第6单元正比例和反比例能力提升卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 B C C C B C
1.B
【分析】成正比例关系的量,一种量扩大或缩小,另一种量也扩大或缩小,相对应的两个数的比值(商)一定;成反比例关系的量,变化方向相反,相对应的两个数的乘积一定。
【详解】b=k×a,b是一定的,则k和a的乘积是一定的,那么k和a成反比例关系。
故答案为:B
【点睛】此题考查的是正比例关系的量和反比例关系的量的判定,解题时注意是比值一定还是积一定。
2.C
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;据此解答。
【详解】选项A,车轮行驶的路程∶转数=车轮周长(比值一定),所以车轮周长一定时,车轮行驶的路程和转数成正比例;
选项B,出勤人数+未出勤人数=全班人数(和一定),不符合正反比例的意义,所以一(5)班今天的出勤人数和未出勤人数不成比例;
选项C,加工每个零件所用时间×零件总个数=工作时间(乘积一定),所以工作时间一定时,加工零件总数和加工每个零件的时间成反比例;
选项D,圆柱的体积∶圆柱的底面积=圆柱的高(比值一定),所以圆柱体的高一定时,它的底面积和体积成正比例;
综上可得:两种量成反比例关系的是C。
故答案为:C
【点睛】本题主要考查辨别正比例的量和反比例的量,解答此类问题时首先确定两种量是否是相关联的量,其次是要看这两种量是对应的比值一定还是乘积一定。
3.C
【分析】图中,横坐标表示长方形的长,纵坐标表示长方形的宽,长和宽都在变化,根据长和宽的数据来判断是面积一定还是周长一定。
【详解】当长是12厘米时,宽是3厘米,其面积是36平方厘米;周长是30厘米。
当长是6厘米时,宽是6厘米,其面积是36平方厘米;周长是24厘米。
由此可以看出长方形的面积是不变的,周长发生了变化,长和宽也变化了,形状也跟着变化了,故选择:C。
【点睛】长方形的面积=长×宽,当面积一定时,长和宽成反比例关系。成反比例的两个量的图像是一条如图所示的曲线。
4.C
【解析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例;无上述两种情况,则不成比例。
【详解】周长=直径×π=2×π×半径,圆面积=半径×半径×π,直径=半径×2;
选项A:圆的半径与直径比值一定,成正比例,
选项B:圆的半径与周长比值一定,成正比例;
选项C:圆的半径与面积,不成比例;
选项D:圆的直径与周长比值一定,成正比例。
故答案选择:C。
【点睛】需熟练掌握正比例和反比例的概念是解题的关键。
5.B
【分析】根据题意可知,硬币的总高度÷硬币的数量=每枚硬币的高度(一定),据此可知硬币的总高度和硬币的数量成正比例,列比例为x∶1000000=1.9∶10,然后解比例即可,最后把单位换算。
【详解】解:设一百万枚1元硬币摞在一起大约有x厘米高。
x∶1000000=1.9∶10
10x=1000000×1.9
10x=1900000
x=1900000÷10
x=190000
190000厘米=1900米=1.9千米
一百万枚1元硬币摞在一起大约1900米高。
故答案为:B
【点睛】本题可用比例解决问题,判断相关的量是正比例还是反比例是解答本题的关键。
6.C
【分析】如果X和Y成反比例,则XY的乘积一定,求出8与12的积,再除以10即可;如果X和Y成正比例,则XY的比值一定,求出8与12的比值,再用10除以比值即可
【详解】8×12÷10
=96÷10
=9.6
8∶12=8÷12=
10÷
=10×
=15
即如果X和Y成反比例,空缺处填9.6;如果X和Y成正比例,空缺处填15。
故答案为:C
【点睛】本题主要考查正反比例的简单应用。
7.(1)
(2)×
(3)×
(4)
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】(1)放水量÷放水的时间=自来水管内水的流速(一定),则放水的时间和放水量成正比例;
(2)圆的面积÷它的半径=π×半径(不一定),是对应的比值不一定,所以圆的面积和它的半径不成比例;
(3)运出的质量+剩下的质量=仓库存粮的总质量(一定),是对应的和一定,所以运出的吨数和剩下的吨数不成比例;
(4)xy=5(一定),是乘积一定,则x和y成反比例。
8. 反 60 2 20 6
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系;正比例图象是一条过原点的直线,反比例图象是一条光滑的曲线,据此结合给出的曲线解答;根据两个点所对应的单价和数量进行填写,据此解答。
【详解】给出的图象是一条光滑的曲线,所以曲线表示反比例关系。
点A表示单价是60元,能买2本;点B表示单价是20元,能买6本。
9. 350 350 路程 速度 时间 反
【分析】用速度×时间,分别求出这辆汽车第一次行驶的速度和时间的积和第二次行驶的速度和时间的积;两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果这两种量的积一定,这两种量就成反比例关系,据此分析。
【详解】70×5=350(千米)、87.5×4=350(千米),速度×时间=路程
这辆汽车第一次行驶的速度和时间的积是350千米,第二次行驶的速度和时间的积是350千米。路程一定,速度和时间成反比例。
10.4
【分析】从图中可知,此时支架平衡,即支架左右两边相等;可得出等量关系:右边的孔数×右边挂的珠子数量=左边的孔数×左边挂的珠子数量上,据此列出反比例方程,并求解。
【详解】解:设右侧第3个孔应挂颗珠才能保持平衡。
3=4×3
3=12
=12÷3
=4
右侧第3个孔应挂4颗珠才能保持平衡。
11. 正 反
【分析】判断两种量成正比例还是成反比例,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。先根据比例的基本性质,把转化成;把∶3=10∶转化成。再根据正、反比例的意义解答。
【详解】因为,所以,即和的比值一定,所以和成正比例;
因为∶3=10∶,所以=30,即和的乘积一定,所以和成反比例。
12.反
【分析】根据题意,总人数一定,每行人数和所站行数成反比例。
【详解】
(行)
所以能站10行。
每行站的人数和能站多少行成反比例关系。
【点睛】本题主要考查反比例、正比例的辨别,关键是看相关联的两个量的乘积一定还是比值一定。
13.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】正方形的周长÷边长=4(一定),比值一定,所以正方形的边长和它的周长成正比例。
所以原题说法错误。
故答案为:×
14.√
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系,用式子表示为:=k;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系,用式子表示为:xy=k;如果两种关系都不满足,则这两种量不成比例;据此解答。
【详解】铺地面积÷地砖的块数==每块地砖的面积(一定),铺地面积和地砖的块数的比值一定,所以它们成正比例;原说法正确。
故答案为:√
15.√
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果xy=k(一定),x和y成反比例关系,据此分析。
【详解】车轮的周长×转动的周数=前进的距离(一定),所以车轮的周长和转动的周数成反比例。原题说法正确。
故答案为:√
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,则成正比例;如果是乘积一定,则成反比例。据此判断。
【详解】加工效率×加工时间=加工一批零件(一定)
因此,加工一批零件,加工效率和加工时间成反比例。原题说法正确。
故答案为:√
17.×
【分析】绳子的长度一定时,剪去的绳子和剩下的绳子不成正比例。 这是因为剪去的绳子长度和剩下的绳子长度之和是固定的,即绳子的总长度一定。这种关系不符合正比例的定义(即两种量的比值一定)。据此判断即可。
【详解】绳子的长度一定,剪去的绳子和剩下的绳子不成正比例。所以原题说法错误。
故答案为:×
18.384根
【分析】根据题意可知,自来水管道的全长不变,即每根管道的长度×根数=自来水管道的全长(一定),乘积一定,那么每根管道的长度与根数成反比例,据此列出反比例方程,并求解。
【详解】解:设可更换旧管根。
5=8×240
5=1920
=1920÷5
=384
答:可更换旧管384根。
19.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
20.96块
【分析】根据题意可知,会议室的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即两种量成反比例;设如果改用边长是5分米的方砖要用x块,列比例:5×5×x=16×150,解比例,即可解答。
【详解】解:设如果改用边长是5分米的方砖要用x块。
5×5×x=16×150
25x=2400
x=2400÷25
x=96
答:如果改用边长是5分米的方砖要用96块。
【点睛】此题首先利用正、反比例的意义判定两种量的关系,解答时关键不要把边长当作面积进行计算。
21.12.5米
【分析】首先根据速度×时间=路程,可得时间一定时,速度和路程成正比例,据此求出乙和丙的速度的比;然后设当乙到终点时,丙还有x米,根据乙丙跑的路程的比=乙丙的速度比,列出比例,求出当乙到终点时,丙还有多少米即可。
【详解】80∶(100-30)
=80∶70
=8∶7
解:设当乙到终点时,丙还有x米,
100∶(100-x)=8∶7
8×(100-x)=100×7
800-8x=700
800-8x+8x=700+8x
700+8x=800
700+8x-700=800-700
8x=100
8x÷8=100÷8
x=12.5
答:丙离终点还有12.5米。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出乙丙的速度的比是多少。
22.(1)见详解;
(2)单价;正;
(3)360
【分析】(1)由统计表可知:《数学报》的单价是40元,根据单价×数量=总价,分别求出4份、5份的总价,填表即可,根据统计表中数据描点连线即可;
(2)由统计表可知:总价÷数量=单价(40元)不变,据此解答。
(3)根据总价=单价×数量直接计算即可。
【详解】(1)4×40=160(元)
5×40=200(元)
填表画图如下:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 160 200 240 280 …
(2)题目中单价没变,总价和数量成正比例。
(3)40×9=360(元)
【点睛】本题主要考查正比例的意义与辨识及统计图表的综合应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例能力提升卷-2024-2025学年数学六年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.假如b=k×a,b是一定的,a、b、k均不为0,下列说法正确的是( )。
A.a和k成正比例关系 B.k和a成反比例关系
C.a和k不成比例 D.无法判断
2.下列各项中,两种量成反比例关系的是( )。
A.车轮周长一定,车轮行驶的路程和转数。
B.一(5)班今天的出勤人数和未出勤人数。
C.工作时间一定,加工零件总数和加工每个零件的时间。
D.圆柱体的高一定,它的底面积和体积。
3.各种长方形,考虑长和宽的关系,下边的图像相当于下面的哪种情况,( )。
A.长一定的长方形 B.周长一定的长方形
C.面积一定的长方形 D.形状一定的长方形
4.下列各选项的两个量,不成正比例的是( )。
A.圆的半径与直径 B.圆的半径与周长
C.圆的半径与面积 D.圆的直径与周长
5.10枚硬币摞在一起高1.9厘米,照这样推算,一百万枚1元硬币摞在一起大约有多高( )。
A.190米 B.1900米 C.19千米 D.190千米
6.下表中如果X和Y成反比例,空缺处填( );如果X和Y成正比例,空缺处填( )。
X 8 10
Y 12
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
二、填空题
7.下面各题中的两种量,成正比例的画“”,成反比例的画“”,不成比例的画“×”。
(1)自来水管内水的流速一定,放水的时间和放水量( )。
(2)圆的半径和面积( )。
(3)仓库存粮的总质量一定,运出的质量和剩下的质量( )。
(4)已知xy=5,x和y( )。
8.
图中的曲线表示( )比例关系。点A表示单价是( )元,能买( )本;点B表示单价是( )元,能买( )本。
9.一辆汽车从甲地开往乙地,如果每小时行70千米,那么5小时到达;如果每小时行87.5千米,那么4小时到达。这辆汽车第一次行驶的速度和时间的积是( )千米,第二次行驶的速度和时间的积是( )千米。( )一定,( )和( )成( )比例。
10.小明在数学实践课中,利用硬纸条做了一个平衡支架开展数学实验。如果在支架左侧第4个孔挂3颗珠,右侧第3个孔应挂( )颗珠才能保持平衡。
11.如果,那么和成( )比例;如果∶3=10∶,那么和成( )比例。
12.六年级同学做广播操,每行站15人,可以站12行。如果每行站18人,能站多少行?此题中,每行站的人数和能站多少行成( )比例关系。
三、判断题
13.正方形的边长和它的周长不成比例。( )
14.每块地砖的面积一定,地砖的块数和铺地面积成正比例。( )
15.车轮前进的距离一定,车轮的周长和转动的周数成反比例。( )
16.加工一批零件,加工效率和加工时间成反比例。( )
17.绳子的长度一定,剪去的绳子和剩下的绳子成正比例。( )
四、解答题
18.自来水公司修建自来水管道,用8米长的新管更换原来5米长的旧管。现在有240根新管,可更换旧管多少根?
19.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
20.学校会议室用方砖铺地,用面积16平方分米的方砖,需要150块,如果改用边长是5分米的方砖要用多少块?(用比例解)
21.甲、乙、丙三人进行100米短跑赛。甲到终点时,乙跑了80米,丙离终点30米。那么,当乙到终点时,丙离终点还有多远?(用比例解)
22.订阅《数学报》的数量和总价的关系如下表:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 240 280 …
(1)将表格补充完整,根据表中的数据,在下图中描出《数学报》总价和数量所对应的点,再按顺序连接起来。
(2)题目中( )没变,总价和数量成( )比例。
(3)从图中可以推算出,如果订阅9份《数学报》,需要( )元。
《第6单元正比例和反比例能力提升卷-2024-2025学年数学六年级下册苏教版》参考答案
题号 1 2 3 4 5 6
答案 B C C C B C
1.B
【分析】成正比例关系的量,一种量扩大或缩小,另一种量也扩大或缩小,相对应的两个数的比值(商)一定;成反比例关系的量,变化方向相反,相对应的两个数的乘积一定。
【详解】b=k×a,b是一定的,则k和a的乘积是一定的,那么k和a成反比例关系。
故答案为:B
【点睛】此题考查的是正比例关系的量和反比例关系的量的判定,解题时注意是比值一定还是积一定。
2.C
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;据此解答。
【详解】选项A,车轮行驶的路程∶转数=车轮周长(比值一定),所以车轮周长一定时,车轮行驶的路程和转数成正比例;
选项B,出勤人数+未出勤人数=全班人数(和一定),不符合正反比例的意义,所以一(5)班今天的出勤人数和未出勤人数不成比例;
选项C,加工每个零件所用时间×零件总个数=工作时间(乘积一定),所以工作时间一定时,加工零件总数和加工每个零件的时间成反比例;
选项D,圆柱的体积∶圆柱的底面积=圆柱的高(比值一定),所以圆柱体的高一定时,它的底面积和体积成正比例;
综上可得:两种量成反比例关系的是C。
故答案为:C
【点睛】本题主要考查辨别正比例的量和反比例的量,解答此类问题时首先确定两种量是否是相关联的量,其次是要看这两种量是对应的比值一定还是乘积一定。
3.C
【分析】图中,横坐标表示长方形的长,纵坐标表示长方形的宽,长和宽都在变化,根据长和宽的数据来判断是面积一定还是周长一定。
【详解】当长是12厘米时,宽是3厘米,其面积是36平方厘米;周长是30厘米。
当长是6厘米时,宽是6厘米,其面积是36平方厘米;周长是24厘米。
由此可以看出长方形的面积是不变的,周长发生了变化,长和宽也变化了,形状也跟着变化了,故选择:C。
【点睛】长方形的面积=长×宽,当面积一定时,长和宽成反比例关系。成反比例的两个量的图像是一条如图所示的曲线。
4.C
【解析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例;无上述两种情况,则不成比例。
【详解】周长=直径×π=2×π×半径,圆面积=半径×半径×π,直径=半径×2;
选项A:圆的半径与直径比值一定,成正比例,
选项B:圆的半径与周长比值一定,成正比例;
选项C:圆的半径与面积,不成比例;
选项D:圆的直径与周长比值一定,成正比例。
故答案选择:C。
【点睛】需熟练掌握正比例和反比例的概念是解题的关键。
5.B
【分析】根据题意可知,硬币的总高度÷硬币的数量=每枚硬币的高度(一定),据此可知硬币的总高度和硬币的数量成正比例,列比例为x∶1000000=1.9∶10,然后解比例即可,最后把单位换算。
【详解】解:设一百万枚1元硬币摞在一起大约有x厘米高。
x∶1000000=1.9∶10
10x=1000000×1.9
10x=1900000
x=1900000÷10
x=190000
190000厘米=1900米=1.9千米
一百万枚1元硬币摞在一起大约1900米高。
故答案为:B
【点睛】本题可用比例解决问题,判断相关的量是正比例还是反比例是解答本题的关键。
6.C
【分析】如果X和Y成反比例,则XY的乘积一定,求出8与12的积,再除以10即可;如果X和Y成正比例,则XY的比值一定,求出8与12的比值,再用10除以比值即可
【详解】8×12÷10
=96÷10
=9.6
8∶12=8÷12=
10÷
=10×
=15
即如果X和Y成反比例,空缺处填9.6;如果X和Y成正比例,空缺处填15。
故答案为:C
【点睛】本题主要考查正反比例的简单应用。
7.(1)
(2)×
(3)×
(4)
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】(1)放水量÷放水的时间=自来水管内水的流速(一定),则放水的时间和放水量成正比例;
(2)圆的面积÷它的半径=π×半径(不一定),是对应的比值不一定,所以圆的面积和它的半径不成比例;
(3)运出的质量+剩下的质量=仓库存粮的总质量(一定),是对应的和一定,所以运出的吨数和剩下的吨数不成比例;
(4)xy=5(一定),是乘积一定,则x和y成反比例。
8. 反 60 2 20 6
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系;正比例图象是一条过原点的直线,反比例图象是一条光滑的曲线,据此结合给出的曲线解答;根据两个点所对应的单价和数量进行填写,据此解答。
【详解】给出的图象是一条光滑的曲线,所以曲线表示反比例关系。
点A表示单价是60元,能买2本;点B表示单价是20元,能买6本。
9. 350 350 路程 速度 时间 反
【分析】用速度×时间,分别求出这辆汽车第一次行驶的速度和时间的积和第二次行驶的速度和时间的积;两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果这两种量的积一定,这两种量就成反比例关系,据此分析。
【详解】70×5=350(千米)、87.5×4=350(千米),速度×时间=路程
这辆汽车第一次行驶的速度和时间的积是350千米,第二次行驶的速度和时间的积是350千米。路程一定,速度和时间成反比例。
10.4
【分析】从图中可知,此时支架平衡,即支架左右两边相等;可得出等量关系:右边的孔数×右边挂的珠子数量=左边的孔数×左边挂的珠子数量上,据此列出反比例方程,并求解。
【详解】解:设右侧第3个孔应挂颗珠才能保持平衡。
3=4×3
3=12
=12÷3
=4
右侧第3个孔应挂4颗珠才能保持平衡。
11. 正 反
【分析】判断两种量成正比例还是成反比例,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。先根据比例的基本性质,把转化成;把∶3=10∶转化成。再根据正、反比例的意义解答。
【详解】因为,所以,即和的比值一定,所以和成正比例;
因为∶3=10∶,所以=30,即和的乘积一定,所以和成反比例。
12.反
【分析】根据题意,总人数一定,每行人数和所站行数成反比例。
【详解】
(行)
所以能站10行。
每行站的人数和能站多少行成反比例关系。
【点睛】本题主要考查反比例、正比例的辨别,关键是看相关联的两个量的乘积一定还是比值一定。
13.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】正方形的周长÷边长=4(一定),比值一定,所以正方形的边长和它的周长成正比例。
所以原题说法错误。
故答案为:×
14.√
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两个量中相对应的两个数的比值一定,这两种量叫作成正比例的量,它们的关系叫作正比例关系,用式子表示为:=k;如果这两个量中相对应的两个数的乘积一定,这两种量叫作成反比例的量,它们的关系叫作反比例关系,用式子表示为:xy=k;如果两种关系都不满足,则这两种量不成比例;据此解答。
【详解】铺地面积÷地砖的块数==每块地砖的面积(一定),铺地面积和地砖的块数的比值一定,所以它们成正比例;原说法正确。
故答案为:√
15.√
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果xy=k(一定),x和y成反比例关系,据此分析。
【详解】车轮的周长×转动的周数=前进的距离(一定),所以车轮的周长和转动的周数成反比例。原题说法正确。
故答案为:√
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,则成正比例;如果是乘积一定,则成反比例。据此判断。
【详解】加工效率×加工时间=加工一批零件(一定)
因此,加工一批零件,加工效率和加工时间成反比例。原题说法正确。
故答案为:√
17.×
【分析】绳子的长度一定时,剪去的绳子和剩下的绳子不成正比例。 这是因为剪去的绳子长度和剩下的绳子长度之和是固定的,即绳子的总长度一定。这种关系不符合正比例的定义(即两种量的比值一定)。据此判断即可。
【详解】绳子的长度一定,剪去的绳子和剩下的绳子不成正比例。所以原题说法错误。
故答案为:×
18.384根
【分析】根据题意可知,自来水管道的全长不变,即每根管道的长度×根数=自来水管道的全长(一定),乘积一定,那么每根管道的长度与根数成反比例,据此列出反比例方程,并求解。
【详解】解:设可更换旧管根。
5=8×240
5=1920
=1920÷5
=384
答:可更换旧管384根。
19.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
20.96块
【分析】根据题意可知,会议室的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即两种量成反比例;设如果改用边长是5分米的方砖要用x块,列比例:5×5×x=16×150,解比例,即可解答。
【详解】解:设如果改用边长是5分米的方砖要用x块。
5×5×x=16×150
25x=2400
x=2400÷25
x=96
答:如果改用边长是5分米的方砖要用96块。
【点睛】此题首先利用正、反比例的意义判定两种量的关系,解答时关键不要把边长当作面积进行计算。
21.12.5米
【分析】首先根据速度×时间=路程,可得时间一定时,速度和路程成正比例,据此求出乙和丙的速度的比;然后设当乙到终点时,丙还有x米,根据乙丙跑的路程的比=乙丙的速度比,列出比例,求出当乙到终点时,丙还有多少米即可。
【详解】80∶(100-30)
=80∶70
=8∶7
解:设当乙到终点时,丙还有x米,
100∶(100-x)=8∶7
8×(100-x)=100×7
800-8x=700
800-8x+8x=700+8x
700+8x=800
700+8x-700=800-700
8x=100
8x÷8=100÷8
x=12.5
答:丙离终点还有12.5米。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出乙丙的速度的比是多少。
22.(1)见详解;
(2)单价;正;
(3)360
【分析】(1)由统计表可知:《数学报》的单价是40元,根据单价×数量=总价,分别求出4份、5份的总价,填表即可,根据统计表中数据描点连线即可;
(2)由统计表可知:总价÷数量=单价(40元)不变,据此解答。
(3)根据总价=单价×数量直接计算即可。
【详解】(1)4×40=160(元)
5×40=200(元)
填表画图如下:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 160 200 240 280 …
(2)题目中单价没变,总价和数量成正比例。
(3)40×9=360(元)
【点睛】本题主要考查正比例的意义与辨识及统计图表的综合应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
