期中检测卷(含解析)-2024-2025学年数学九年级下册人教版
文档属性
| 名称 | 期中检测卷(含解析)-2024-2025学年数学九年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中检测卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数的图像( )
A.过原点的一条直线 B.位于一、三象限的两支曲线
C.位于二、四象限的两支曲线 D.过点和点的一条直线
2.已知与相似,,则的长可能是( )
A.2 B.4.5 C.9 D.9.6
3.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
4.的值等于( )
A. B. C. D.
5.已知,如图所示的一张三角形纸片,边的长为,边上的高为,在三角形纸片中从下往上依次裁剪去宽为的矩形纸条.若剪得的其中一张纸条是正方形,则这张正方形纸条是( )
A.第5张 B.第6张 C.第7张 D.第8张
6.如图,在平面直角坐标系中,的顶点A的坐标为,边经过原点O,轴,若反比例函数的图象经过点A和边的中点P,则的长为( )
A.12 B.9 C.8 D.2
7.如图,的对角线、交于点以为直径的半圆经过点,若的周长为,,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
8.已知,正比例函数的图象与双曲线交于点A、B.点A与点C关于x轴对称,连接,若的面积为12,则k的值为 .
9.已知四边形四边形,且,若四边形的周长为15,则四边形的周长为 .
10.如图,在平面直角坐标系中,反比例函数的图像与矩形的边,分别相交于点,,已知,,的面积为,则的面积为 .
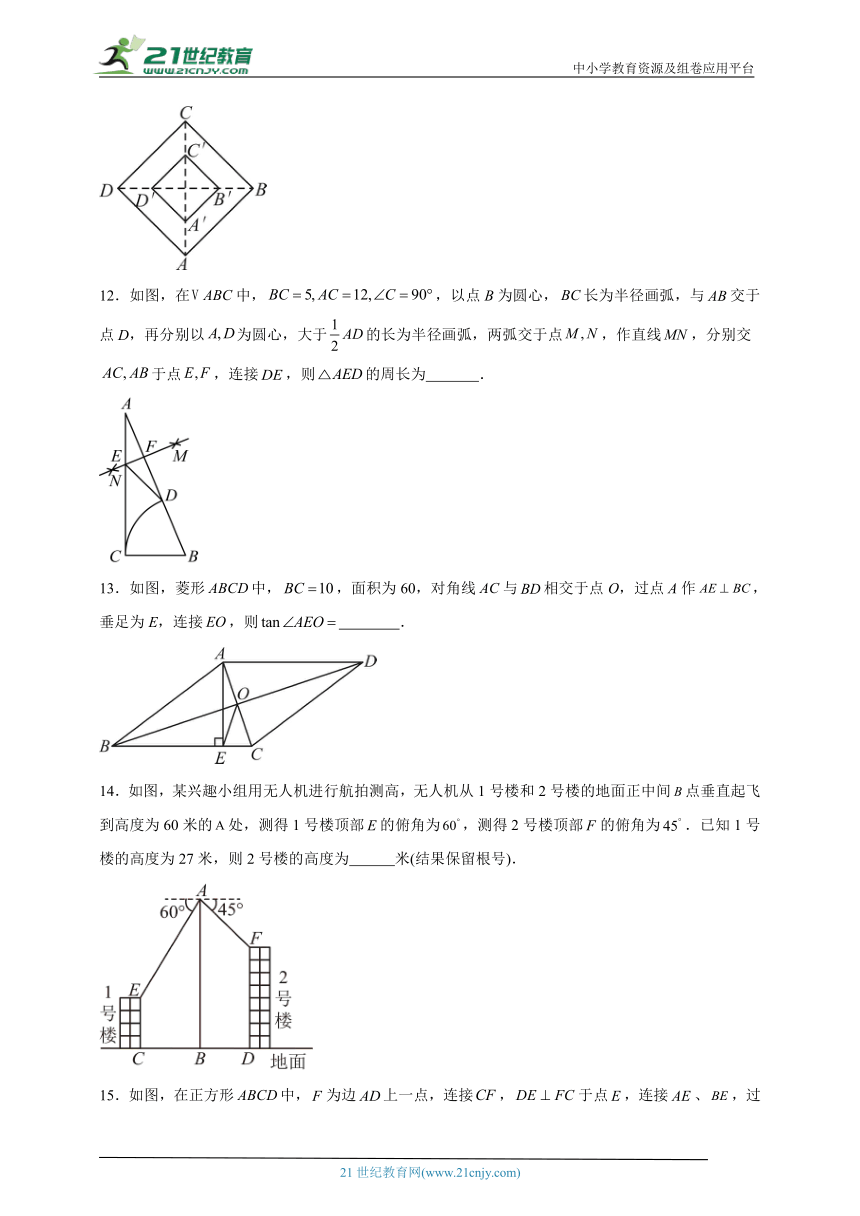
11.如图,正方形的面积为,以它的对角线的交点为位似中心,作它的位似图形四边形.若,则四边形的面积为 .
12.如图,在中,,以点B为圆心,长为半径画弧,与交于点D,再分别以为圆心,大于的长为半径画弧,两弧交于点,作直线,分别交于点,连接,则的周长为 .
13.如图,菱形中,,面积为60,对角线与相交于点O,过点A作,垂足为E,连接,则 .
14.如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间点垂直起飞到高度为60米的处,测得1号楼顶部的俯角为,测得2号楼顶部的俯角为.已知1号楼的高度为27米,则2号楼的高度为 米(结果保留根号).
15.如图,在正方形中,为边上一点,连接,于点,连接、,过作于点,已知,,,则的长为 .
三、解答题
16.计算:
17.如图,在平面直角坐标系中,O为坐标原点.已知反比例函数的图象经过点,过点A作轴于点B,且的面积为.
(1)求k和m的值;
(2)当时,求函数值y的取值范围.
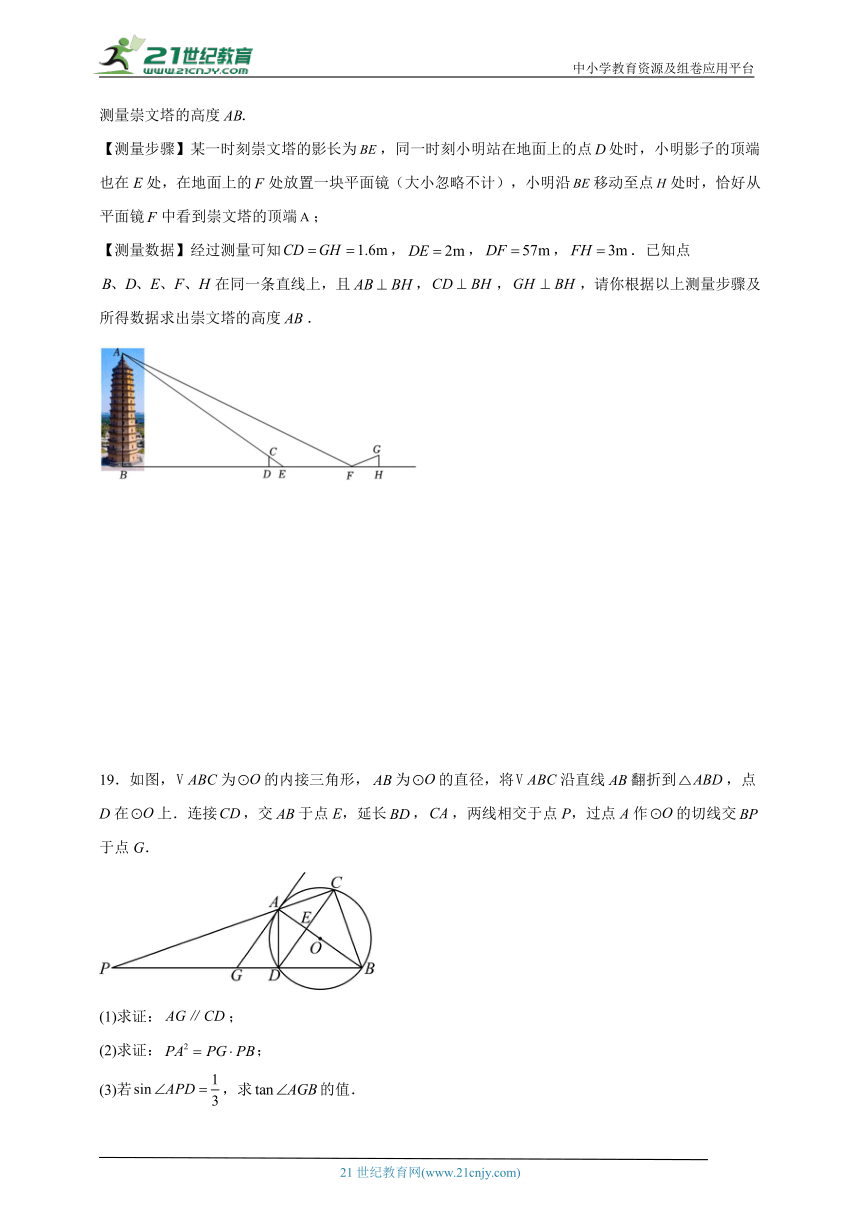
18.如图,某数学兴趣小组利用相似的知识和光的反射定律(反射角等于入射角)在综合实践活动中测量崇文塔的高度
【测量步骤】某一时刻崇文塔的影长为,同一时刻小明站在地面上的点处时,小明影子的顶端也在E处,在地面上的处放置一块平面镜(大小忽略不计),小明沿移动至点处时,恰好从平面镜中看到崇文塔的顶端;
【测量数据】经过测量可知,,,.已知点在同一条直线上,且,,,请你根据以上测量步骤及所得数据求出崇文塔的高度.
19.如图,为的内接三角形,为的直径,将沿直线翻折到,点D在上.连接,交于点E,延长,,两线相交于点P,过点A作的切线交于点G.
(1)求证:;
(2)求证:;
(3)若,求的值.
20.如图,在平面直角坐标系中,正比例函数的图象与反比例函数()的图象相交于、两点,轴于点,点的坐标为,连接、.
(1)求该反比例函数的表达式;
(2)在该反比例函数的图象上是否存在点,使得的面积与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
21.如图,四边形中,,,平分,点,分别在,上,,交的延长线于点.
(1)求证:四边形为菱形;
(2)求证:;
(3)如图2,连接交于点,若,,当时,求的值.
22.如图1,小丽设计了一个探究杠杆平衡条件的实验:取一根匀质木杆,用细绳绑在木杆的中点处,并将其吊起.在中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,直至木杆平衡,改变弹簧秤与点的距离,重复上述步骤,观察弹簧秤的示数的变化情况.实验数据记录如下:
… 4 6 8 10 12 …
… 9 6 4.5 3.6 3 …
(1)把表中,的各组对应值作为点的坐标,在如图2所示的平面直角坐标系中描出相应的点,用平滑的曲线连接这些点并观察所得的图象,求出与之间的函数关系式;
(2)当弹簧秤的示数为时,弹簧秤与点的距离是多少?在弹簧的弹性限度内,随着弹簧秤与点的距离逐渐减小,弹簧秤的示数将发生怎样的变化?
《期中检测卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 C C D A A C C
1.C
【分析】本题考查了反比例函数的图像与性质,熟练掌握该知识点是解题的关键.根据函数关系式,可确定该函数图像是双曲线可判断A、D选项,再根据的正负确定双曲线所在象限可判断B、C选项.
【详解】解:A、是反比例函数,反比例函数图像不过原点且为双曲线,故该选项错误;
B、因为,所以图像是位于二、四象限的双曲线,故该选项错误;
C、因为,所以图像是位于二、四象限的双曲线,故该选项正确;
D、的图像是双曲线,不是直线,故该选项错误;
故选:C.
2.C
【分析】此题考查了相似三角形的性质,根据与相似,由对应边成比例分三种情况列出比例式求解即可求得的长,解题的关键是熟练掌握相似三角形的性质,注意分情况讨论.
【详解】解:当时,
∴,即,
则;
当时,
∴,即,
则;
当时,
∴,即,
则;
故选:C.
3.D
【分析】本题考查了反比例函数图象上的点的坐标特征,比较函数值的大小,熟练掌握知识点是解题的关键.
将点,,代入,分别求出,即可比较大小.
【详解】解:∵点,,都在反比例函数的图象上,
∴将点,,代入,得,
∴,
故选:D.
4.A
【分析】本题考查了涉及特殊角的三角函数值的计算,二次根式的乘法计算,正确记忆特殊角的三角函数值是解题的关键.分别代入特殊角的三角函数值,再计算即可.
【详解】解:
,
故选:A.
5.A
【分析】本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
【详解】解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是4,
所以根据相似三角形的性质可设从顶点C到这个正方形的边距离为,
则,
解得,
所以另一段长为,
因为,所以是第5张.
故选:A.
6.C
【分析】本题主要考查了反比例函数与几何综合,根据反比例函数的对称性可得,则由中点坐标计算公式得到,再求出C的坐标即可得到答案.
【详解】解:∵反比例函数的图象经过点A和边的中点P,且边经过原点O,
∴由反比例函数的对称性可知,
∴,
∵轴且,
∴,
∴,
故选:C.
7.C
【分析】本题考查了平行四边形的性质,菱形的判定,扇形面积公式,解直角三角形,掌握知识点的应用是解题的关键.
连接,证明四边形是菱形,再求出,,又,则,最后由即可求解.
【详解】解:连接,
∵为直径的半圆直径,
∴,
∴,
∵四边形是平行四边形,
∴四边形是菱形,
∴,,,
∵的周长为,
∴,
∴,
∴,,
∴,
∴,
∴,
∴
,
故选:.
8.6
【分析】本题考查了反比例函数值的几何意义,连接,设则,可得,即可解答.
【详解】解:如图,连接.设,
正比例函数的图象与双曲线交于点A、B.点A与点C关于x轴对称,
.
轴,轴,
,
.
.
故答案为:6.
9.9
【分析】本题主要考查相似多边的性质,根据周长比等于相似比可得答案.
【详解】解:∵四边形四边形,且,
∴,
∵四边形的周长为15,
∴四边形的周长,
故答案为:9.
10.
【分析】本题考查坐标与图形性质、矩形的性质、反比例图像的性质,熟练掌握矩形的性质,利用割补法求解图形面积是解答的关键.
利用矩形性质和坐标与反比例图像的性质可得M的坐标是,N的坐标是,再根据坐标与图形性质和矩形性质,借助割补法,根据求解面积列方程即可求出.进而求解.
【详解】∵四边形是矩形,,,
∴轴,,,
∵M、在上,
∴M的坐标是,N的坐标是,
∵四边形是矩形,
∴, ,,
∴的面积,
∴,
解得:(负值已经舍去)
故
故答案为.
11.
【分析】本题考查位似变换,利用位似的性质得面积比等于相似比的平方即可求解,解题的关键是理解题意,灵活运用位似的性质.
【详解】解:∵,
∴正方形的面积四边形的面积,
∵正方形的面积为,
∴四边形的面积为,
故答案为:.
12./
【分析】本题考查作图基本作图、勾股定理、线段垂直平分线、相似三角形的判定与性质,熟练掌握相关知识点是解答本题的关键.由题意得,,直线为线段的垂直平分线,由勾股定理得,进而可得,证明,可得,即,求出,即可得出答案.
【详解】解:由题意得,,直线为线段的垂直平分线,
∴,,
,,,
,
,
,
,,
,
,
即,
解得,
∴,
∴.
故答案为:.
13.
【分析】本题考查了菱形的性质,勾股定理,直角三角形斜边的中线,解直角三角形.根据菱形的面积公式结合的长度即可得出、、的长度,再利用勾股定理求出的长度,再根据直角三角形斜边上的中线等于斜边的一半得到,则,据此根据正切的定义即可得出答案.
【详解】解:∵四边形为菱形,
∴,,
∵,
∴,,
∴.
∵,
∴,
∴(负值已舍去),
∴,
∵,
∴,
∴或(舍去).
∴,
∴,
∵,,
∴,
∴,
∴。
故答案为:.
14.
【分析】本题考查了三角函数的应用;由题意得米,米,过点作于点,过点作于点,则,,四边形和四边形均为矩形,,得出米,,,,推出,再由锐角三角函数的定义求出米,易证是等腰直角三角形,得出米,即可得出结果.
【详解】解:由题意得:米,米,
如图,过点作于点,过点作于点,
∴,,四边形和四边形均为矩形,,
米,,,,
为的中点,
,
,
在中,(米),
(米),
米,
,,
是等腰直角三角形,
米,
(米),
故答案为:.
15.
【分析】根据正方形的性质,同角的余角相等,推出,得到,根据三角函数结合勾股定理求出,进而得到,过点作,三线合一结合勾股定理,求出的长,再利用等积法求出的长即可.
【详解】解:∵正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
在中,,
∵,,
∴,
∴为的中点,
∴,
∵,,,
∴,
∴,
过点作,则:,
∴,
∴,
∴
;
∵,
∴,
∴;
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,解直角三角形,等腰三角形的判定和性质,熟练掌握相关知识点,利用同角的余角相等,进行导角,是解题的关键.
16.7
【分析】本题考查实数的混合运算,先进行特殊角的三角函数,零指数幂,去绝对值,负整数指数幂,开方运算,再进行加减运算即可.
【详解】解:原式.
17.(1),
(2)
【分析】根据三角形的面积公式先得到m的值,然后把点A的坐标代入,可求出k的值;
求出时,y的值,再根据反比例函数的性质求解.
【详解】(1)解:,
,,
∴,
,
点A的坐标为,
把代入,得;
(2)解:∵当时,,
又反比例函数在时,y随x的增大而减小,
当时,y的取值范围为
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,点在图象上,点的横纵坐标满足图象的解析式,解决此题的关键是要熟练掌握反比例函数的图象性质.
18.
【分析】此题考查了相似三角形的应用,由和,可以证得,即可证得,即得,由光的反射的性质可以得出,再结合和 ,可以证得,进而根据相似三角形的性质即可求解,掌握相似三角形的判定和性质是解题的关键.
【详解】解:,,
,
,
,,
,
,
,
,,
,
,
,,
,
又,
,
,
即,
,
解得,
答:崇文塔的高度为,
19.(1)见解析
(2)见解析
(3)
【分析】(1)根据折叠可得,根据切线的定义可得,即可得证;
(2)根据题意证明,进而证明,根据相似三角形的性质,即可得证;
(3)根据,设,则,得出,根据折叠的性质可得出,则,进而求得,根据,进而根据正切的定义,即可求解.
【详解】(1)证明:∵将沿直线翻折到,
∴.
∵为的直径,是切线,
∴.
∴.
(2)证明:∵
∴
∵
∴
又∵,
∴.
∴,即;
(3)解:∵,设,则,
∴.
∴.
由折叠可得,
∴.
∵在中,,
∴.
∵,,
∴.
∴.
【点睛】本题考查了切线的性质,折叠问题,相似三角形的性质与判定,解直角三角形,圆周角定理,平行线的判定与性质等知识,熟练掌握以上知识是解题的关键.
20.(1)
(2)存在,点的坐标为或
【分析】本题考查了反比例函数的图象与性质,正比例函数的图象与性质,三角形的面积,解题的关键是掌握相关知识.
(1)由轴于点,得到的横坐标为,将其代入正比例函数中,求出,再将代入反比例函数中,求出,即可求解;
(2)联立正比例函数与反比例函数,求出,,结合,,得到,,进而得出,,根据“的面积与的面积相等”列方程求出,即可求解.
【详解】(1)解:轴于点,
的横坐标为,
在正比例函数中,令,则,
,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)存在,
联立,
解得:或,
,,
,,
,,
,,
的面积与的面积相等,
,
解得:或,
在反比例函数的图象上存在点,使得的面积与的面积相等,点的坐标为或.
21.(1)详见解析
(2)详见解析
(3)
【分析】(1)结合平行线的性质以及角平分线的定义,得,再运用四边相等的四边形是菱形,进行作答即可.
(2)先得出,再结合平行线的性质以及角的等量代换得,最后运用两组角分别相等的三角形是相似三角形,即可作答.
(3)由(2)可知,,结合勾股定理列式,解得.得再因为,得,即.过点作于点,证明四边形是矩形,则,得出.
【详解】(1)证明:,平分,
,,
,
,
又,
,
四边形为菱形.
(2)证明:,
,
.
又,
,
.
,
,
,
即.
(3)解:由(2)可知,,
设.
,
,
解得.
,
,
,
.
过点作于点,如图,
∵,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
则,,
,
∵,
.
【点睛】本题考查了菱形的判定,相似三角形的判定与性质,勾股定理,矩形的性质与判定,平行线分线段成比例,正确掌握相关性质内容是解题的关键.
22.(1)画图见解析,
(2);弹簧秤的示数将不断增大
【分析】本题考查了画反比例函数图象,反比例函数的性质及其应用,由图象判断出y与x之间的函数关系是解题的关键.
(1)根据表格数值描点、连线即可画出图形 ,根据图象特点判断出y与x之间的函数关系,最后利用待定系数法求出函数解析式即可;
(2)把代入(1)所得函数解析式即可求出x,根据函数的性质即可判断弹簧秤示数的变化情况;
【详解】(1)解∶画图如下∶
由图可得,y是x的反比例函数,设,把代入得,
,
解得,
∴;
(2)解∶把代入,得,
积的,
即当弹簧秤的示数为时,弹簧秤与O点的距离是,
∵,在第一象限内,y的值随着x的值的增大而减小,
∴随着弹簧秤与O点的距离不断减小,弹簧秤的示数将不断增大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中检测卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数的图像( )
A.过原点的一条直线 B.位于一、三象限的两支曲线
C.位于二、四象限的两支曲线 D.过点和点的一条直线
2.已知与相似,,则的长可能是( )
A.2 B.4.5 C.9 D.9.6
3.若点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
4.的值等于( )
A. B. C. D.
5.已知,如图所示的一张三角形纸片,边的长为,边上的高为,在三角形纸片中从下往上依次裁剪去宽为的矩形纸条.若剪得的其中一张纸条是正方形,则这张正方形纸条是( )
A.第5张 B.第6张 C.第7张 D.第8张
6.如图,在平面直角坐标系中,的顶点A的坐标为,边经过原点O,轴,若反比例函数的图象经过点A和边的中点P,则的长为( )
A.12 B.9 C.8 D.2
7.如图,的对角线、交于点以为直径的半圆经过点,若的周长为,,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
8.已知,正比例函数的图象与双曲线交于点A、B.点A与点C关于x轴对称,连接,若的面积为12,则k的值为 .
9.已知四边形四边形,且,若四边形的周长为15,则四边形的周长为 .
10.如图,在平面直角坐标系中,反比例函数的图像与矩形的边,分别相交于点,,已知,,的面积为,则的面积为 .
11.如图,正方形的面积为,以它的对角线的交点为位似中心,作它的位似图形四边形.若,则四边形的面积为 .
12.如图,在中,,以点B为圆心,长为半径画弧,与交于点D,再分别以为圆心,大于的长为半径画弧,两弧交于点,作直线,分别交于点,连接,则的周长为 .
13.如图,菱形中,,面积为60,对角线与相交于点O,过点A作,垂足为E,连接,则 .
14.如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间点垂直起飞到高度为60米的处,测得1号楼顶部的俯角为,测得2号楼顶部的俯角为.已知1号楼的高度为27米,则2号楼的高度为 米(结果保留根号).
15.如图,在正方形中,为边上一点,连接,于点,连接、,过作于点,已知,,,则的长为 .
三、解答题
16.计算:
17.如图,在平面直角坐标系中,O为坐标原点.已知反比例函数的图象经过点,过点A作轴于点B,且的面积为.
(1)求k和m的值;
(2)当时,求函数值y的取值范围.
18.如图,某数学兴趣小组利用相似的知识和光的反射定律(反射角等于入射角)在综合实践活动中测量崇文塔的高度
【测量步骤】某一时刻崇文塔的影长为,同一时刻小明站在地面上的点处时,小明影子的顶端也在E处,在地面上的处放置一块平面镜(大小忽略不计),小明沿移动至点处时,恰好从平面镜中看到崇文塔的顶端;
【测量数据】经过测量可知,,,.已知点在同一条直线上,且,,,请你根据以上测量步骤及所得数据求出崇文塔的高度.
19.如图,为的内接三角形,为的直径,将沿直线翻折到,点D在上.连接,交于点E,延长,,两线相交于点P,过点A作的切线交于点G.
(1)求证:;
(2)求证:;
(3)若,求的值.
20.如图,在平面直角坐标系中,正比例函数的图象与反比例函数()的图象相交于、两点,轴于点,点的坐标为,连接、.
(1)求该反比例函数的表达式;
(2)在该反比例函数的图象上是否存在点,使得的面积与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
21.如图,四边形中,,,平分,点,分别在,上,,交的延长线于点.
(1)求证:四边形为菱形;
(2)求证:;
(3)如图2,连接交于点,若,,当时,求的值.
22.如图1,小丽设计了一个探究杠杆平衡条件的实验:取一根匀质木杆,用细绳绑在木杆的中点处,并将其吊起.在中点左侧固定位置处悬挂重物,在中点右侧用一个弹簧秤向下拉,直至木杆平衡,改变弹簧秤与点的距离,重复上述步骤,观察弹簧秤的示数的变化情况.实验数据记录如下:
… 4 6 8 10 12 …
… 9 6 4.5 3.6 3 …
(1)把表中,的各组对应值作为点的坐标,在如图2所示的平面直角坐标系中描出相应的点,用平滑的曲线连接这些点并观察所得的图象,求出与之间的函数关系式;
(2)当弹簧秤的示数为时,弹簧秤与点的距离是多少?在弹簧的弹性限度内,随着弹簧秤与点的距离逐渐减小,弹簧秤的示数将发生怎样的变化?
《期中检测卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 C C D A A C C
1.C
【分析】本题考查了反比例函数的图像与性质,熟练掌握该知识点是解题的关键.根据函数关系式,可确定该函数图像是双曲线可判断A、D选项,再根据的正负确定双曲线所在象限可判断B、C选项.
【详解】解:A、是反比例函数,反比例函数图像不过原点且为双曲线,故该选项错误;
B、因为,所以图像是位于二、四象限的双曲线,故该选项错误;
C、因为,所以图像是位于二、四象限的双曲线,故该选项正确;
D、的图像是双曲线,不是直线,故该选项错误;
故选:C.
2.C
【分析】此题考查了相似三角形的性质,根据与相似,由对应边成比例分三种情况列出比例式求解即可求得的长,解题的关键是熟练掌握相似三角形的性质,注意分情况讨论.
【详解】解:当时,
∴,即,
则;
当时,
∴,即,
则;
当时,
∴,即,
则;
故选:C.
3.D
【分析】本题考查了反比例函数图象上的点的坐标特征,比较函数值的大小,熟练掌握知识点是解题的关键.
将点,,代入,分别求出,即可比较大小.
【详解】解:∵点,,都在反比例函数的图象上,
∴将点,,代入,得,
∴,
故选:D.
4.A
【分析】本题考查了涉及特殊角的三角函数值的计算,二次根式的乘法计算,正确记忆特殊角的三角函数值是解题的关键.分别代入特殊角的三角函数值,再计算即可.
【详解】解:
,
故选:A.
5.A
【分析】本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.根据相似三角形的相似比求得顶点到这个正方形的长,再根据矩形的宽求得是第几张.
【详解】解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是4,
所以根据相似三角形的性质可设从顶点C到这个正方形的边距离为,
则,
解得,
所以另一段长为,
因为,所以是第5张.
故选:A.
6.C
【分析】本题主要考查了反比例函数与几何综合,根据反比例函数的对称性可得,则由中点坐标计算公式得到,再求出C的坐标即可得到答案.
【详解】解:∵反比例函数的图象经过点A和边的中点P,且边经过原点O,
∴由反比例函数的对称性可知,
∴,
∵轴且,
∴,
∴,
故选:C.
7.C
【分析】本题考查了平行四边形的性质,菱形的判定,扇形面积公式,解直角三角形,掌握知识点的应用是解题的关键.
连接,证明四边形是菱形,再求出,,又,则,最后由即可求解.
【详解】解:连接,
∵为直径的半圆直径,
∴,
∴,
∵四边形是平行四边形,
∴四边形是菱形,
∴,,,
∵的周长为,
∴,
∴,
∴,,
∴,
∴,
∴,
∴
,
故选:.
8.6
【分析】本题考查了反比例函数值的几何意义,连接,设则,可得,即可解答.
【详解】解:如图,连接.设,
正比例函数的图象与双曲线交于点A、B.点A与点C关于x轴对称,
.
轴,轴,
,
.
.
故答案为:6.
9.9
【分析】本题主要考查相似多边的性质,根据周长比等于相似比可得答案.
【详解】解:∵四边形四边形,且,
∴,
∵四边形的周长为15,
∴四边形的周长,
故答案为:9.
10.
【分析】本题考查坐标与图形性质、矩形的性质、反比例图像的性质,熟练掌握矩形的性质,利用割补法求解图形面积是解答的关键.
利用矩形性质和坐标与反比例图像的性质可得M的坐标是,N的坐标是,再根据坐标与图形性质和矩形性质,借助割补法,根据求解面积列方程即可求出.进而求解.
【详解】∵四边形是矩形,,,
∴轴,,,
∵M、在上,
∴M的坐标是,N的坐标是,
∵四边形是矩形,
∴, ,,
∴的面积,
∴,
解得:(负值已经舍去)
故
故答案为.
11.
【分析】本题考查位似变换,利用位似的性质得面积比等于相似比的平方即可求解,解题的关键是理解题意,灵活运用位似的性质.
【详解】解:∵,
∴正方形的面积四边形的面积,
∵正方形的面积为,
∴四边形的面积为,
故答案为:.
12./
【分析】本题考查作图基本作图、勾股定理、线段垂直平分线、相似三角形的判定与性质,熟练掌握相关知识点是解答本题的关键.由题意得,,直线为线段的垂直平分线,由勾股定理得,进而可得,证明,可得,即,求出,即可得出答案.
【详解】解:由题意得,,直线为线段的垂直平分线,
∴,,
,,,
,
,
,
,,
,
,
即,
解得,
∴,
∴.
故答案为:.
13.
【分析】本题考查了菱形的性质,勾股定理,直角三角形斜边的中线,解直角三角形.根据菱形的面积公式结合的长度即可得出、、的长度,再利用勾股定理求出的长度,再根据直角三角形斜边上的中线等于斜边的一半得到,则,据此根据正切的定义即可得出答案.
【详解】解:∵四边形为菱形,
∴,,
∵,
∴,,
∴.
∵,
∴,
∴(负值已舍去),
∴,
∵,
∴,
∴或(舍去).
∴,
∴,
∵,,
∴,
∴,
∴。
故答案为:.
14.
【分析】本题考查了三角函数的应用;由题意得米,米,过点作于点,过点作于点,则,,四边形和四边形均为矩形,,得出米,,,,推出,再由锐角三角函数的定义求出米,易证是等腰直角三角形,得出米,即可得出结果.
【详解】解:由题意得:米,米,
如图,过点作于点,过点作于点,
∴,,四边形和四边形均为矩形,,
米,,,,
为的中点,
,
,
在中,(米),
(米),
米,
,,
是等腰直角三角形,
米,
(米),
故答案为:.
15.
【分析】根据正方形的性质,同角的余角相等,推出,得到,根据三角函数结合勾股定理求出,进而得到,过点作,三线合一结合勾股定理,求出的长,再利用等积法求出的长即可.
【详解】解:∵正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
在中,,
∵,,
∴,
∴为的中点,
∴,
∵,,,
∴,
∴,
过点作,则:,
∴,
∴,
∴
;
∵,
∴,
∴;
故答案为:.
【点睛】本题考查正方形的性质,勾股定理,解直角三角形,等腰三角形的判定和性质,熟练掌握相关知识点,利用同角的余角相等,进行导角,是解题的关键.
16.7
【分析】本题考查实数的混合运算,先进行特殊角的三角函数,零指数幂,去绝对值,负整数指数幂,开方运算,再进行加减运算即可.
【详解】解:原式.
17.(1),
(2)
【分析】根据三角形的面积公式先得到m的值,然后把点A的坐标代入,可求出k的值;
求出时,y的值,再根据反比例函数的性质求解.
【详解】(1)解:,
,,
∴,
,
点A的坐标为,
把代入,得;
(2)解:∵当时,,
又反比例函数在时,y随x的增大而减小,
当时,y的取值范围为
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,点在图象上,点的横纵坐标满足图象的解析式,解决此题的关键是要熟练掌握反比例函数的图象性质.
18.
【分析】此题考查了相似三角形的应用,由和,可以证得,即可证得,即得,由光的反射的性质可以得出,再结合和 ,可以证得,进而根据相似三角形的性质即可求解,掌握相似三角形的判定和性质是解题的关键.
【详解】解:,,
,
,
,,
,
,
,
,,
,
,
,,
,
又,
,
,
即,
,
解得,
答:崇文塔的高度为,
19.(1)见解析
(2)见解析
(3)
【分析】(1)根据折叠可得,根据切线的定义可得,即可得证;
(2)根据题意证明,进而证明,根据相似三角形的性质,即可得证;
(3)根据,设,则,得出,根据折叠的性质可得出,则,进而求得,根据,进而根据正切的定义,即可求解.
【详解】(1)证明:∵将沿直线翻折到,
∴.
∵为的直径,是切线,
∴.
∴.
(2)证明:∵
∴
∵
∴
又∵,
∴.
∴,即;
(3)解:∵,设,则,
∴.
∴.
由折叠可得,
∴.
∵在中,,
∴.
∵,,
∴.
∴.
【点睛】本题考查了切线的性质,折叠问题,相似三角形的性质与判定,解直角三角形,圆周角定理,平行线的判定与性质等知识,熟练掌握以上知识是解题的关键.
20.(1)
(2)存在,点的坐标为或
【分析】本题考查了反比例函数的图象与性质,正比例函数的图象与性质,三角形的面积,解题的关键是掌握相关知识.
(1)由轴于点,得到的横坐标为,将其代入正比例函数中,求出,再将代入反比例函数中,求出,即可求解;
(2)联立正比例函数与反比例函数,求出,,结合,,得到,,进而得出,,根据“的面积与的面积相等”列方程求出,即可求解.
【详解】(1)解:轴于点,
的横坐标为,
在正比例函数中,令,则,
,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)存在,
联立,
解得:或,
,,
,,
,,
,,
的面积与的面积相等,
,
解得:或,
在反比例函数的图象上存在点,使得的面积与的面积相等,点的坐标为或.
21.(1)详见解析
(2)详见解析
(3)
【分析】(1)结合平行线的性质以及角平分线的定义,得,再运用四边相等的四边形是菱形,进行作答即可.
(2)先得出,再结合平行线的性质以及角的等量代换得,最后运用两组角分别相等的三角形是相似三角形,即可作答.
(3)由(2)可知,,结合勾股定理列式,解得.得再因为,得,即.过点作于点,证明四边形是矩形,则,得出.
【详解】(1)证明:,平分,
,,
,
,
又,
,
四边形为菱形.
(2)证明:,
,
.
又,
,
.
,
,
,
即.
(3)解:由(2)可知,,
设.
,
,
解得.
,
,
,
.
过点作于点,如图,
∵,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
则,,
,
∵,
.
【点睛】本题考查了菱形的判定,相似三角形的判定与性质,勾股定理,矩形的性质与判定,平行线分线段成比例,正确掌握相关性质内容是解题的关键.
22.(1)画图见解析,
(2);弹簧秤的示数将不断增大
【分析】本题考查了画反比例函数图象,反比例函数的性质及其应用,由图象判断出y与x之间的函数关系是解题的关键.
(1)根据表格数值描点、连线即可画出图形 ,根据图象特点判断出y与x之间的函数关系,最后利用待定系数法求出函数解析式即可;
(2)把代入(1)所得函数解析式即可求出x,根据函数的性质即可判断弹簧秤示数的变化情况;
【详解】(1)解∶画图如下∶
由图可得,y是x的反比例函数,设,把代入得,
,
解得,
∴;
(2)解∶把代入,得,
积的,
即当弹簧秤的示数为时,弹簧秤与O点的距离是,
∵,在第一象限内,y的值随着x的值的增大而减小,
∴随着弹簧秤与O点的距离不断减小,弹簧秤的示数将不断增大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
