期中检测卷(含解析)-2024-2025学年数学八年级下册苏科版
文档属性
| 名称 | 期中检测卷(含解析)-2024-2025学年数学八年级下册苏科版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期中检测卷-2024-2025学年数学八年级下册苏科版
学校:___________姓名:___________班级:___________考号:___________
总分:120分 时间:120分钟
一、单选题(共21分)
1.在对个数据进行整理时,把这些数据分成组,则各组的频数之和、频率之和分别为( ).
A.和 B.和 C.和 D.和
2.下列事件中,必然事件是( )
A.下一届奥运会上,跑的世界纪录被打破
B.一年中,31天的月份和30天的月份一样多
C.某种彩票中奖率为,买10000张该种彩票会中奖
D.将豆油滴入水中,豆油浮在水面上
3.下列条件中能判定四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图是某市来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.汽车尾气所占百分比约为建筑扬尘的3倍
B.建筑扬尘占
C.煤炭燃烧释放的所对应扇形统计图的圆心角度数是
D.煤炭燃烧对的影响最大
5.布袋里有 100 个球, 其中有红球 28 个, 绿球 20 个, 黄球 12 个, 蓝球 20 个, 白球 10 个, 黑球 10 个, 从袋中任意摸出球来, 若要一次摸出至少 15 个同色的球, 则需要从袋中摸出球至少( )
A.85 个 B.75个 C. 个 D.16 个
6.如图,在平行四边形中,,,分别以A、C为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线交于点F,交于点E,则的周长是( )
A.7 B.10 C.11 D.12
7.如图,在平面直角坐标系中,已知正方形,,点D为x轴上一动点,以为边在的右侧作等腰,,连接,则的最小值为( )
A. B. C.2 D.4
二、填空题(共24分)
8.已知数据:,,,,0.其中无理数出现的频率为 .
9.杜牧《清明》诗中写道“清明时节雨纷纷”,从数学的观点看,诗句中描述的事件是 事件.(填“必然”、“不可能”或“随机”)
10.某校用简单随机抽样的方法调查了学生最喜爱的四种球类运动,并根据统计结果绘制成扇形统计图(如图).若调查的人数中最喜欢乒乓球的有20人,则最喜欢篮球的有 人.
11.与关于原点成中心对称,点的对称点分别是,若,则的范围是 .
12.在一个不透明的袋子中装有仅颜色不同的8个小球,其中红球3个,黑球5个.若先从袋子中取出个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件.那么,当 时,事件为随机事件.
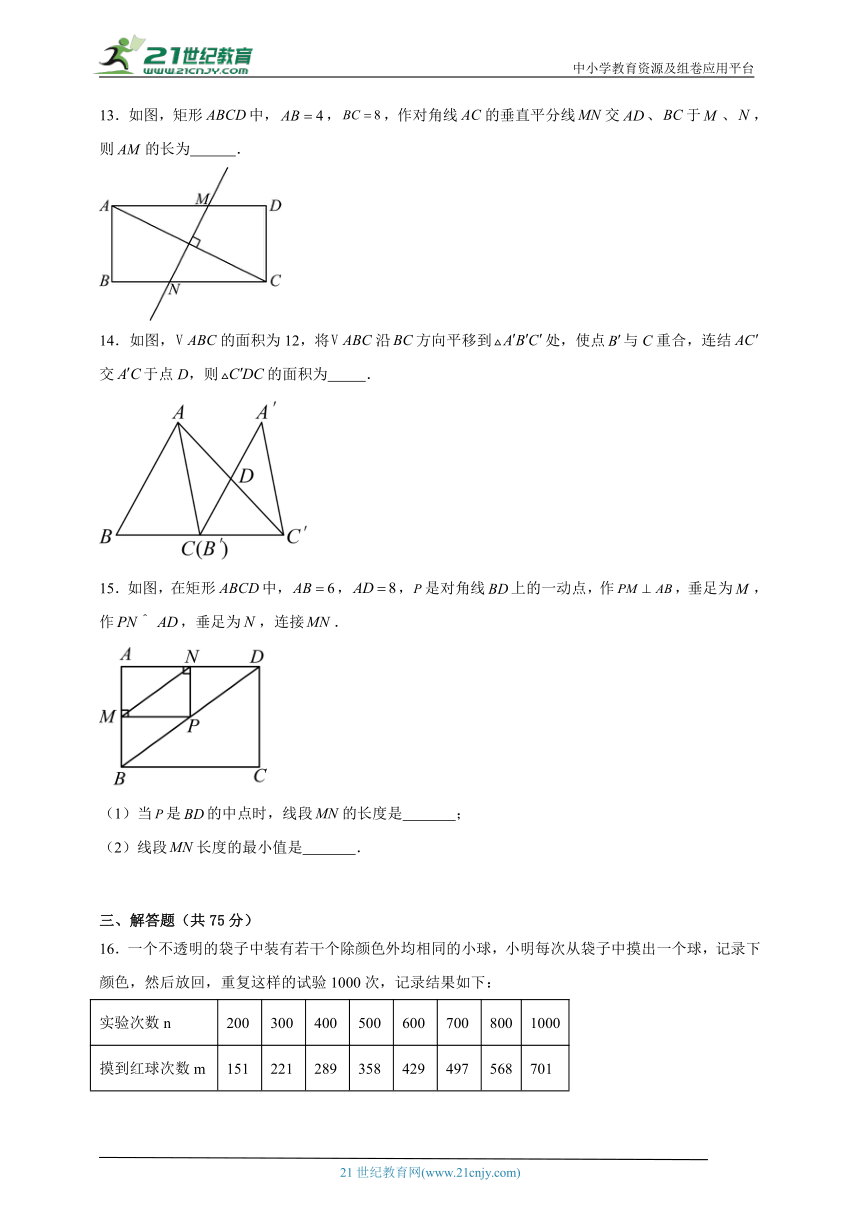
13.如图,矩形中,,,作对角线的垂直平分线交、于、,则的长为 .
14.如图,的面积为12,将沿方向平移到处,使点与C重合,连结交于点D,则的面积为 .
15.如图,在矩形中,,,是对角线上的一动点,作,垂足为,作,垂足为,连接.
(1)当是的中点时,线段的长度是 ;
(2)线段长度的最小值是 .
三、解答题(共75分)
16.一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 568 701
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a=________,b=_________;
(2)估计从袋子中摸出一个球恰好是红球的概率约为________;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?
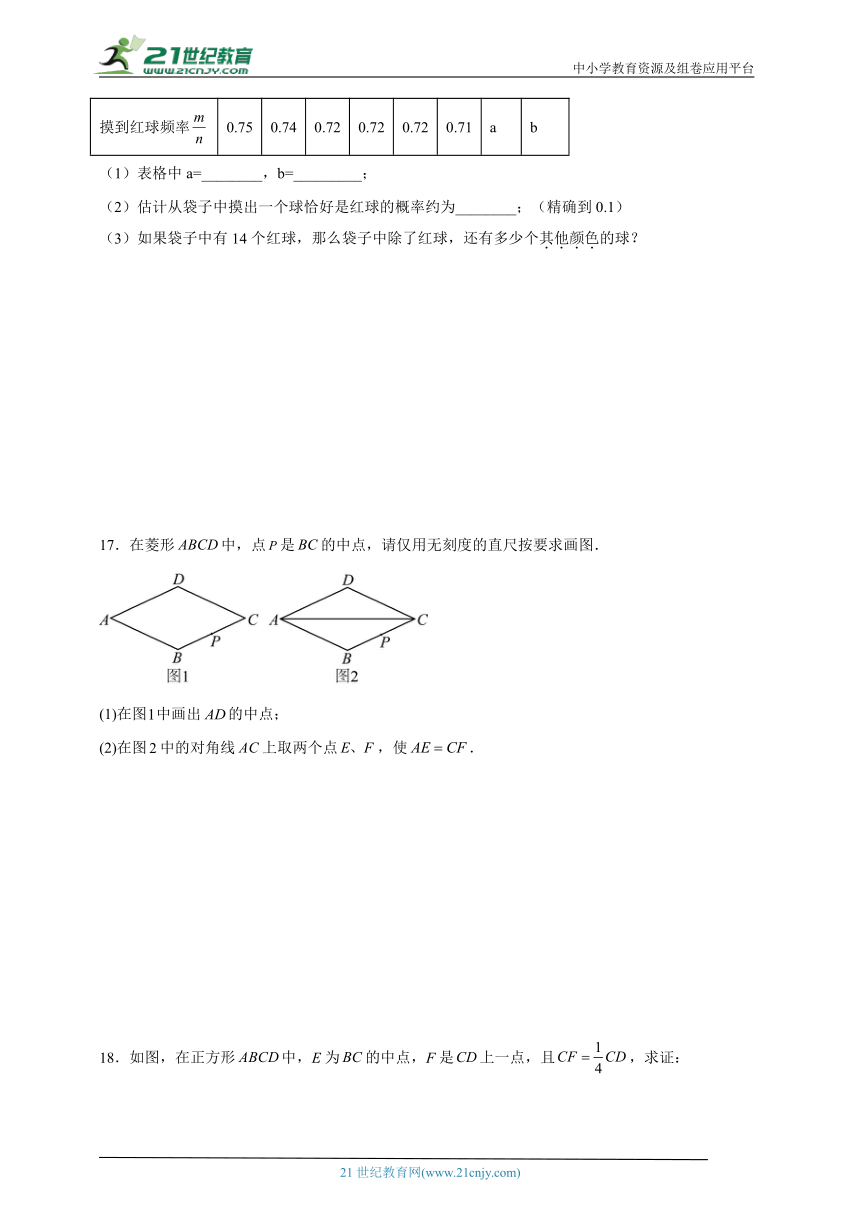
17.在菱形中,点是的中点,请仅用无刻度的直尺按要求画图.
(1)在图中画出的中点;
(2)在图中的对角线上取两个点,使.
18.如图,在正方形中,E为的中点,F是上一点,且,求证:
(1);
(2).
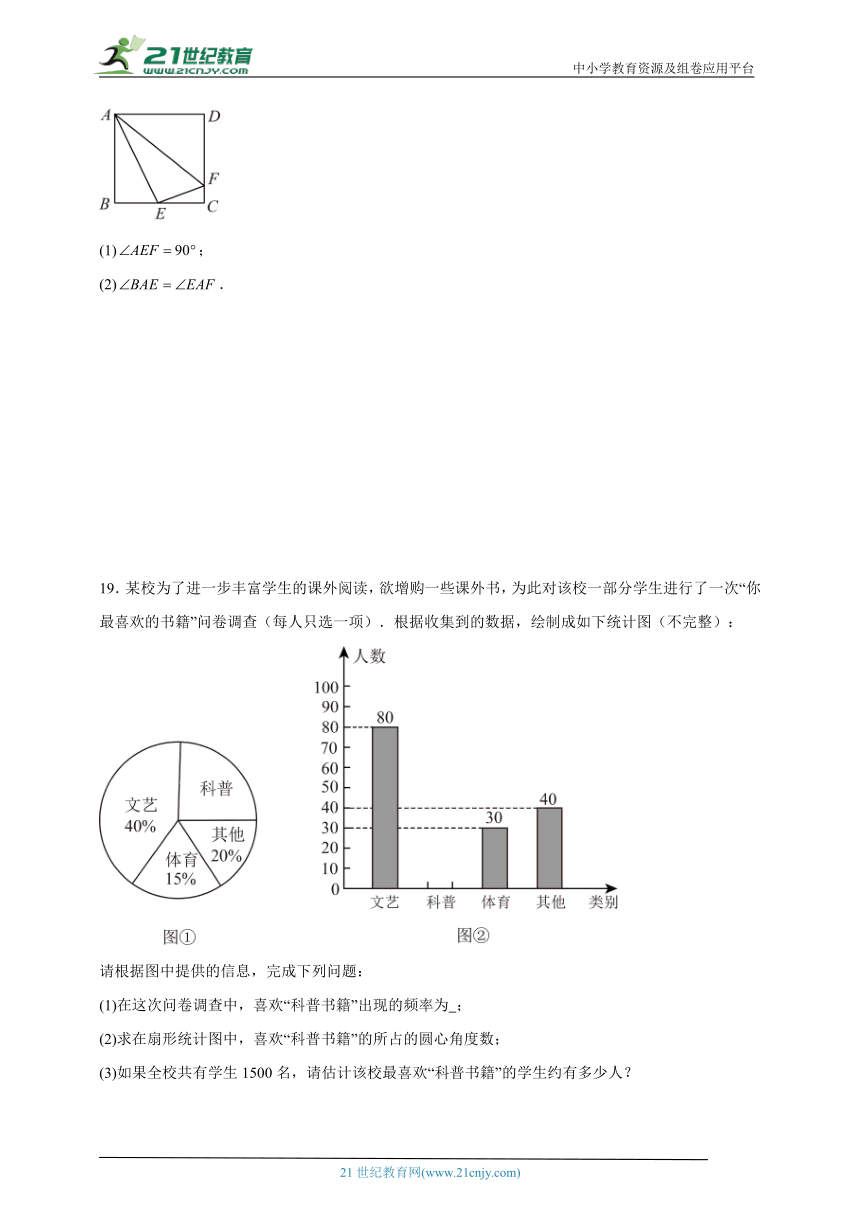
19.某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为 ;
(2)求在扇形统计图中,喜欢“科普书籍”的所占的圆心角度数;
(3)如果全校共有学生1500名,请估计该校最喜欢“科普书籍”的学生约有多少人?
20.如图,在中,,是中线,是的外角的平分线,,垂足为.
(1)求证:四边形是矩形;
(2)与之间的关系是什么?请说明理由.
21.已知在中,,,点D为直线上一动点(点D不与B,C重合),以为边作正方形,连接.
(1)如图1,当点D在线段上时,求证:
(2)如图2,当点D在线段的延长线上时,请判断三条线段之间的数量关系,并说明理由.
(3)如图2,延长交于点G,连接,若已知,,求的长.
《期中检测卷-2024-2025学年数学八年级下册苏科版》参考答案
题号 1 2 3 4 5 6 7
答案 A D D C B B B
1.A
【分析】本题考查的知识点是频数的概念,解题关键是熟练掌握频数的概念.
根据频数的概念即可得解.
【详解】根据频数的概念,各小组频数之和等于数据总和,即,
根据频率频数总数,得各小组频率之和等于.
故选:.
2.D
【分析】必然事件就是一定发生的事件,根据定义即可解答.本题考查了事件的分类,必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:A、下一届奥运会上,跑的世界纪录被打破是随机事件,不符合题意;
B、一年中大月份有7个,小月份有5个,一年中,31天的月份和30天的月份一样多是不可能事件,不符合题意;
C、某种彩票中奖率为,买10000张该种彩票会中奖是随机事件,尽管中奖率是1%,不符合题意;
D、常温下油的密度<水的密度,所以将豆油滴入水中,豆油浮在水面上,是必然事件,符合题意.
故选:D.
3.D
【分析】本题主要考查了平行四边形的判定定理,熟知平行四边形的判定定理是解题的关键.根据平行四边形的判定方法,逐项进行判断即可.
【详解】解:A.由,,一组对边平行,另一组对边相等,不能判定四边形是平行四边形,故A不符合题意;
B.由,,不能判定四边形是平行四边形,故B不符合题意;
C.由,不能判定四边形是平行四边形,故C不符合题意;
D.由,,能判定四边形是平行四边形,故D符合题意.
故选:D.
4.C
【分析】本题主要考查扇形统计图,正确获取扇形统计图中的信息是解题关键.根据扇形统计图中的进行计算,然后再逐项判断即可.
【详解】解:A.建筑扬尘占,汽车尾气所占百分比约为建筑扬尘的5倍,故此选项不符合题意;
B.建筑扬尘占,故此选项不符合题意;
C.,即煤炭燃烧释放的所对应扇形统计图的圆心角度数是,故此选项符合题意;
D.汽车尾气排放对的影响最大,故此选项不符合题意.
故选:C.
5.B
【分析】此题考查的知识点是推理与论证,关键是考虑最差情况先摸出9个黑球,14个白球,再摸出另三色中一色的14个球,此时再任意摸出一个小球即可保证15个小球颜色相同.
根据事件发生可能性大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.这里要考虑最差情况.
【详解】解:最坏情况考虑就行了,摸出14个红球,14个绿球,12个黄球,14个蓝球,10个白球,10个黑球,最后再摸出任意一个球,这时可以保证至少有15个颜色相同,即最少要摸:个球;
故选B.
6.B
【分析】本题考查了作图-基本作图(垂直平分线)和平行四边形性质,要熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角,作已知线段的垂直平分线,作已知角的角平分线,过一点作已知直线的垂线)的方法.利用垂直平分线的作法得垂直平分,则,利用等线段代换得到的周长,然后根据平行四边形的性质可确定周长的值.
【详解】解:∵四边形是平行四边形,
∴,,
∵由作法可知,直线是线段的垂直平分线,
∴,
∴,
∴的周长.
故选B.
7.B
【分析】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质,作轴于H,连接.证明,得出,即,推出点在的角平分线所在直线上运动,作,则是等腰直角三角形,由正方形的性质可得,求出,即可得解.
【详解】解:如图,作轴于H,连接.
∵,
∴,,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴点在的角平分线所在直线上运动,
作于M,则是等腰直角三角形,
∵正方形,,
∴,
∴,即的最小值为,
故选:B.
8./
【分析】此题主要考查了频率与频数以及无理数.直接利用无理数的定义得出无理数的个数,进而利用频率求法得出答案.
【详解】解:,
∴数据,,,,0中,无理数有:,共2个,
故无理数出现的频率为:.
故答案为:.
9.随机
【分析】本题考查了随机事件的概念,解题的关键是明确必然事件,不可能事件,随机事件的定义.
必然事件是指在一定条件下必然会发生的事件;不可能事件是指在一定条件下必然不会发生的事件;随机事件是指在一定条件下,可能发生也可能不发生的事件.判断诗句描述的事件类型,依据随机事件的定义分析.
【详解】“清明时节雨纷纷”描述的是清明时节下雨的情况,在现实中,清明时节可能下雨,也可能不下雨,其发生具有不确定性,符合随机事件的定义.因此,诗句中描述的事件是随机事件.
故答案为:随机.
10.16
【分析】本题考查了从扇形统计图中获取信息,由扇形统计图得最喜欢乒乓球的有20人占,可求出调查学生的总人数,然后用总人数乘以最喜欢篮球所占百分比即可.
【详解】解:(人),
故答案为:16.
11.
【分析】此题主要考查了中心对称图形的性质以及三角形三边关系,利用关于原点成中心对称图形的性质得出,进而利用三角形三边关系得出答案.熟练掌握中心对称图形的性质以及三角形三边关系是解决问题的关键.
【详解】解:∵与关于原点成中心对称,点的对称点分别是,,
∴,
∴在中,由三角形三边关系可知的范围是:
故答案为:.
12.2
【分析】本题考查了随机事件,熟练掌握随机事件,必然事件,不可能事件的特点是解题的关键.根据随机事件的概念即可得出答案.
【详解】∵事件为随机事件.
∴“摸出黑球”为随机事件,
∴必须留有红球,才能使摸出黑球为随机事件,
∵,
∴m的值是2;
故答案为:2.
13.5
【分析】本题主要考查了勾股定理,矩形的性质,线段垂直平分线的性质,根据线段垂直平分线的性质得到,再由矩形的性质得到的长,设,则,利用勾股定理可得方程,解方程即可得到答案.
【详解】解;∵对角线的垂直平分线交、于、,
∴,
∵四边形是矩形,
∴,,
设,则,
在中,由勾股定理得,
∴,
解得,
∴,
故答案为:5.
14.6
【分析】本题考查了平移的性质、与三角形中线有关的面积的计算,连接,由平移的性质可得:,,,从而得出四边形为平行四边形,由平行四边形的性质可得,即可得解.
【详解】解:如图:连接,
,
由平移的性质可得:,,,
∴四边形为平行四边形,
∴,
∴,
故答案为:.
15.
【分析】本题考查了矩形的性质与判定,勾股定理,垂线段最短;
(1)连接,勾股定理求得,根据直角三角形中,斜边上的中线等于斜边的一半得出,进而根据,得出四边形是矩形,根据矩形的对角线相等,即可求解;
(2)同(1)得出四边形为矩形,当时,取最小值,即最小,根据等面积法即可求解.
【详解】(1)连接,
∵矩形中,,,
∴,,
∵是的中点,
∴,
∵,,,
∴四边形是矩形
∴,
故答案为:.
(2)如图,连接.
,,
.
在矩形中,,
四边形为矩形,
,
的最小值即的最小值.
当时,取最小值.
在中,.
,
,即线段长度的最小值是.
故答案为:.
16.(1)0.71,0.701;(2)0.7;(3)6个.
【分析】(1)直接用摸到红球的次数除以试验次数即可求得摸到红球的频率;
(2)找到多次试验频率逐渐稳定到的常数即可求得概率;
(3)根据题意列出方程求解即可.
【详解】解:(1)a=568÷800=0.71;
b=701÷800=0.701;
(2)观察发现随着实验次数的增多,摸到红球的频率逐渐稳定在常数0.7附近,
所以估计从袋子中摸出一个球恰好是红球的概率约为0.7;
(3)设袋子中除去红球外,还有其他颜色的球x个,根据题意得0.7(x+14)=14,
解得:x=6,
答:袋子中还有其他颜色的球6个.
故答案为(1)0.71,0.701;(2)0.7;(3)6个.
【点睛】此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.(1)见解析
(2)见解析
【分析】本题考查了菱形的性质和无刻度的直尺按要求画图,掌握知识点的应用是解题的关键.
()连接交于点,然后连接,延长交于点,则点即为所求;
()连接交于点,然后连接,延长交于点,连接交于点,连接交于点,则点即为所求.
【详解】(1)解:如图所示,点即为所求;
(2)解:如图所示,点即为所求.
18.(1)见解析
(2)见解析
【分析】本题考查了正方形的性质、勾股定理、勾股定理逆定理、角平分线的判定与性质,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
(1)设,则,,,由勾股定理得出,,,再由勾股定理逆定理判断即可得证;
(2)过点E作于G,由等面积法得出,求出点在的角平分线上,即可得证.
【详解】(1)证明:设,
∵四边形是正方形,
∴,
∵E为的中点,
∴,
∵,
∴,,
∴,,,
∵,,
∴,
∴;
(2)证明:过点E作于G,
∵,
∴,
∴,
又∵,
∴点在的角平分线上,
∴.
19.(1)
(2)
(3)
【分析】本题考查的是条形统计图和扇形统计图的综合运用,用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)根据体育类人数除以体育类所占的百分比,可得被调查的学生人数,再求出喜欢“科普书籍”的人数即可求出喜欢“科普书籍”出现的频率;
(2)用乘以“科普书籍”所占的比例可得“科普书籍”所占的圆心角度数;
(3)用全校人数乘以最喜欢“文艺”书籍的所占的百分比可得答案.
【详解】(1)解:被调查的学生人数为:(人),
喜欢“科普书籍”的人数为(人),
喜欢“科普书籍”出现的频率为;
故答案为:;
(2)解:“科普书籍”所占的圆心角度数为:,
故答案为:;
(3)解:(人),
答:估计该校最喜欢“科普书籍”书籍的学生有人.
20.(1)见解析;
(2),,理由见解析.
【分析】本题考查了矩形的判定与性质,等腰三角形的性质,中位线的性质与判定,熟练掌握以上知识点是解题的关键;
(1)根据等腰三角形三线合一得到,,结合是的外角的平分线,可得出,又由即可得到,然后根据矩形的判断即可得证;
(2)利用矩形的性质可求,根据三角形中线可得,得出是的中位线,即可得出结论.
【详解】(1)证明:中,,是中线,
,,
,
为的外角的平分线,
,
,
即,
,
,
四边形是矩形;
(2)解:,,理由如下:
由(1)知,四边形为矩形,
,
中,是中线,
,
是的中位线,
,.
21.(1)见解析;
(2),理由见解析;
(3)
【分析】(1)证明是等腰直角三角形,利用即可证明,从而证得,据此即可证得结论;
(2)同(1)相同,利用即可证得,从而证得,即可得到;
(3)过点作,过点作,勾股定理求出的长,三线合一求出的长,进而求出的长,根据全等三角形的性质,求出的长,证明为等腰三角形,求出的长,进而求出的长,证明,求出的长,勾股定理求出的长即可.
【详解】(1)证明:∵,,
∴,
∴,
∵四边形是正方形,
∴,,
∵,,
∴,
则在和中,
,
∴
∴,
∵,
∴;
(2);
理由:∵,,
∴,
∴,
∵四边形是正方形,
∴,,
∵,,
∴,
∵在和中,
∴
∴,
∴,
∴;
(3)过点作,过点作,如图:
∵,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
由(2)知:,
∴,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
又∵,,
∴,
∴,,
∴,
∴.
【点睛】本题考查正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,熟练掌握相关知识点,添加辅助线构造全等三角形,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中检测卷-2024-2025学年数学八年级下册苏科版
学校:___________姓名:___________班级:___________考号:___________
总分:120分 时间:120分钟
一、单选题(共21分)
1.在对个数据进行整理时,把这些数据分成组,则各组的频数之和、频率之和分别为( ).
A.和 B.和 C.和 D.和
2.下列事件中,必然事件是( )
A.下一届奥运会上,跑的世界纪录被打破
B.一年中,31天的月份和30天的月份一样多
C.某种彩票中奖率为,买10000张该种彩票会中奖
D.将豆油滴入水中,豆油浮在水面上
3.下列条件中能判定四边形是平行四边形的是( )
A., B.,
C., D.,
4.如图是某市来源统计图,则根据统计图得出的下列判断中,正确的是( )
A.汽车尾气所占百分比约为建筑扬尘的3倍
B.建筑扬尘占
C.煤炭燃烧释放的所对应扇形统计图的圆心角度数是
D.煤炭燃烧对的影响最大
5.布袋里有 100 个球, 其中有红球 28 个, 绿球 20 个, 黄球 12 个, 蓝球 20 个, 白球 10 个, 黑球 10 个, 从袋中任意摸出球来, 若要一次摸出至少 15 个同色的球, 则需要从袋中摸出球至少( )
A.85 个 B.75个 C. 个 D.16 个
6.如图,在平行四边形中,,,分别以A、C为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线交于点F,交于点E,则的周长是( )
A.7 B.10 C.11 D.12
7.如图,在平面直角坐标系中,已知正方形,,点D为x轴上一动点,以为边在的右侧作等腰,,连接,则的最小值为( )
A. B. C.2 D.4
二、填空题(共24分)
8.已知数据:,,,,0.其中无理数出现的频率为 .
9.杜牧《清明》诗中写道“清明时节雨纷纷”,从数学的观点看,诗句中描述的事件是 事件.(填“必然”、“不可能”或“随机”)
10.某校用简单随机抽样的方法调查了学生最喜爱的四种球类运动,并根据统计结果绘制成扇形统计图(如图).若调查的人数中最喜欢乒乓球的有20人,则最喜欢篮球的有 人.
11.与关于原点成中心对称,点的对称点分别是,若,则的范围是 .
12.在一个不透明的袋子中装有仅颜色不同的8个小球,其中红球3个,黑球5个.若先从袋子中取出个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件.那么,当 时,事件为随机事件.
13.如图,矩形中,,,作对角线的垂直平分线交、于、,则的长为 .
14.如图,的面积为12,将沿方向平移到处,使点与C重合,连结交于点D,则的面积为 .
15.如图,在矩形中,,,是对角线上的一动点,作,垂足为,作,垂足为,连接.
(1)当是的中点时,线段的长度是 ;
(2)线段长度的最小值是 .
三、解答题(共75分)
16.一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 568 701
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a=________,b=_________;
(2)估计从袋子中摸出一个球恰好是红球的概率约为________;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?
17.在菱形中,点是的中点,请仅用无刻度的直尺按要求画图.
(1)在图中画出的中点;
(2)在图中的对角线上取两个点,使.
18.如图,在正方形中,E为的中点,F是上一点,且,求证:
(1);
(2).
19.某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为 ;
(2)求在扇形统计图中,喜欢“科普书籍”的所占的圆心角度数;
(3)如果全校共有学生1500名,请估计该校最喜欢“科普书籍”的学生约有多少人?
20.如图,在中,,是中线,是的外角的平分线,,垂足为.
(1)求证:四边形是矩形;
(2)与之间的关系是什么?请说明理由.
21.已知在中,,,点D为直线上一动点(点D不与B,C重合),以为边作正方形,连接.
(1)如图1,当点D在线段上时,求证:
(2)如图2,当点D在线段的延长线上时,请判断三条线段之间的数量关系,并说明理由.
(3)如图2,延长交于点G,连接,若已知,,求的长.
《期中检测卷-2024-2025学年数学八年级下册苏科版》参考答案
题号 1 2 3 4 5 6 7
答案 A D D C B B B
1.A
【分析】本题考查的知识点是频数的概念,解题关键是熟练掌握频数的概念.
根据频数的概念即可得解.
【详解】根据频数的概念,各小组频数之和等于数据总和,即,
根据频率频数总数,得各小组频率之和等于.
故选:.
2.D
【分析】必然事件就是一定发生的事件,根据定义即可解答.本题考查了事件的分类,必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:A、下一届奥运会上,跑的世界纪录被打破是随机事件,不符合题意;
B、一年中大月份有7个,小月份有5个,一年中,31天的月份和30天的月份一样多是不可能事件,不符合题意;
C、某种彩票中奖率为,买10000张该种彩票会中奖是随机事件,尽管中奖率是1%,不符合题意;
D、常温下油的密度<水的密度,所以将豆油滴入水中,豆油浮在水面上,是必然事件,符合题意.
故选:D.
3.D
【分析】本题主要考查了平行四边形的判定定理,熟知平行四边形的判定定理是解题的关键.根据平行四边形的判定方法,逐项进行判断即可.
【详解】解:A.由,,一组对边平行,另一组对边相等,不能判定四边形是平行四边形,故A不符合题意;
B.由,,不能判定四边形是平行四边形,故B不符合题意;
C.由,不能判定四边形是平行四边形,故C不符合题意;
D.由,,能判定四边形是平行四边形,故D符合题意.
故选:D.
4.C
【分析】本题主要考查扇形统计图,正确获取扇形统计图中的信息是解题关键.根据扇形统计图中的进行计算,然后再逐项判断即可.
【详解】解:A.建筑扬尘占,汽车尾气所占百分比约为建筑扬尘的5倍,故此选项不符合题意;
B.建筑扬尘占,故此选项不符合题意;
C.,即煤炭燃烧释放的所对应扇形统计图的圆心角度数是,故此选项符合题意;
D.汽车尾气排放对的影响最大,故此选项不符合题意.
故选:C.
5.B
【分析】此题考查的知识点是推理与论证,关键是考虑最差情况先摸出9个黑球,14个白球,再摸出另三色中一色的14个球,此时再任意摸出一个小球即可保证15个小球颜色相同.
根据事件发生可能性大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.这里要考虑最差情况.
【详解】解:最坏情况考虑就行了,摸出14个红球,14个绿球,12个黄球,14个蓝球,10个白球,10个黑球,最后再摸出任意一个球,这时可以保证至少有15个颜色相同,即最少要摸:个球;
故选B.
6.B
【分析】本题考查了作图-基本作图(垂直平分线)和平行四边形性质,要熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角,作已知线段的垂直平分线,作已知角的角平分线,过一点作已知直线的垂线)的方法.利用垂直平分线的作法得垂直平分,则,利用等线段代换得到的周长,然后根据平行四边形的性质可确定周长的值.
【详解】解:∵四边形是平行四边形,
∴,,
∵由作法可知,直线是线段的垂直平分线,
∴,
∴,
∴的周长.
故选B.
7.B
【分析】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质,作轴于H,连接.证明,得出,即,推出点在的角平分线所在直线上运动,作,则是等腰直角三角形,由正方形的性质可得,求出,即可得解.
【详解】解:如图,作轴于H,连接.
∵,
∴,,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴点在的角平分线所在直线上运动,
作于M,则是等腰直角三角形,
∵正方形,,
∴,
∴,即的最小值为,
故选:B.
8./
【分析】此题主要考查了频率与频数以及无理数.直接利用无理数的定义得出无理数的个数,进而利用频率求法得出答案.
【详解】解:,
∴数据,,,,0中,无理数有:,共2个,
故无理数出现的频率为:.
故答案为:.
9.随机
【分析】本题考查了随机事件的概念,解题的关键是明确必然事件,不可能事件,随机事件的定义.
必然事件是指在一定条件下必然会发生的事件;不可能事件是指在一定条件下必然不会发生的事件;随机事件是指在一定条件下,可能发生也可能不发生的事件.判断诗句描述的事件类型,依据随机事件的定义分析.
【详解】“清明时节雨纷纷”描述的是清明时节下雨的情况,在现实中,清明时节可能下雨,也可能不下雨,其发生具有不确定性,符合随机事件的定义.因此,诗句中描述的事件是随机事件.
故答案为:随机.
10.16
【分析】本题考查了从扇形统计图中获取信息,由扇形统计图得最喜欢乒乓球的有20人占,可求出调查学生的总人数,然后用总人数乘以最喜欢篮球所占百分比即可.
【详解】解:(人),
故答案为:16.
11.
【分析】此题主要考查了中心对称图形的性质以及三角形三边关系,利用关于原点成中心对称图形的性质得出,进而利用三角形三边关系得出答案.熟练掌握中心对称图形的性质以及三角形三边关系是解决问题的关键.
【详解】解:∵与关于原点成中心对称,点的对称点分别是,,
∴,
∴在中,由三角形三边关系可知的范围是:
故答案为:.
12.2
【分析】本题考查了随机事件,熟练掌握随机事件,必然事件,不可能事件的特点是解题的关键.根据随机事件的概念即可得出答案.
【详解】∵事件为随机事件.
∴“摸出黑球”为随机事件,
∴必须留有红球,才能使摸出黑球为随机事件,
∵,
∴m的值是2;
故答案为:2.
13.5
【分析】本题主要考查了勾股定理,矩形的性质,线段垂直平分线的性质,根据线段垂直平分线的性质得到,再由矩形的性质得到的长,设,则,利用勾股定理可得方程,解方程即可得到答案.
【详解】解;∵对角线的垂直平分线交、于、,
∴,
∵四边形是矩形,
∴,,
设,则,
在中,由勾股定理得,
∴,
解得,
∴,
故答案为:5.
14.6
【分析】本题考查了平移的性质、与三角形中线有关的面积的计算,连接,由平移的性质可得:,,,从而得出四边形为平行四边形,由平行四边形的性质可得,即可得解.
【详解】解:如图:连接,
,
由平移的性质可得:,,,
∴四边形为平行四边形,
∴,
∴,
故答案为:.
15.
【分析】本题考查了矩形的性质与判定,勾股定理,垂线段最短;
(1)连接,勾股定理求得,根据直角三角形中,斜边上的中线等于斜边的一半得出,进而根据,得出四边形是矩形,根据矩形的对角线相等,即可求解;
(2)同(1)得出四边形为矩形,当时,取最小值,即最小,根据等面积法即可求解.
【详解】(1)连接,
∵矩形中,,,
∴,,
∵是的中点,
∴,
∵,,,
∴四边形是矩形
∴,
故答案为:.
(2)如图,连接.
,,
.
在矩形中,,
四边形为矩形,
,
的最小值即的最小值.
当时,取最小值.
在中,.
,
,即线段长度的最小值是.
故答案为:.
16.(1)0.71,0.701;(2)0.7;(3)6个.
【分析】(1)直接用摸到红球的次数除以试验次数即可求得摸到红球的频率;
(2)找到多次试验频率逐渐稳定到的常数即可求得概率;
(3)根据题意列出方程求解即可.
【详解】解:(1)a=568÷800=0.71;
b=701÷800=0.701;
(2)观察发现随着实验次数的增多,摸到红球的频率逐渐稳定在常数0.7附近,
所以估计从袋子中摸出一个球恰好是红球的概率约为0.7;
(3)设袋子中除去红球外,还有其他颜色的球x个,根据题意得0.7(x+14)=14,
解得:x=6,
答:袋子中还有其他颜色的球6个.
故答案为(1)0.71,0.701;(2)0.7;(3)6个.
【点睛】此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.(1)见解析
(2)见解析
【分析】本题考查了菱形的性质和无刻度的直尺按要求画图,掌握知识点的应用是解题的关键.
()连接交于点,然后连接,延长交于点,则点即为所求;
()连接交于点,然后连接,延长交于点,连接交于点,连接交于点,则点即为所求.
【详解】(1)解:如图所示,点即为所求;
(2)解:如图所示,点即为所求.
18.(1)见解析
(2)见解析
【分析】本题考查了正方形的性质、勾股定理、勾股定理逆定理、角平分线的判定与性质,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
(1)设,则,,,由勾股定理得出,,,再由勾股定理逆定理判断即可得证;
(2)过点E作于G,由等面积法得出,求出点在的角平分线上,即可得证.
【详解】(1)证明:设,
∵四边形是正方形,
∴,
∵E为的中点,
∴,
∵,
∴,,
∴,,,
∵,,
∴,
∴;
(2)证明:过点E作于G,
∵,
∴,
∴,
又∵,
∴点在的角平分线上,
∴.
19.(1)
(2)
(3)
【分析】本题考查的是条形统计图和扇形统计图的综合运用,用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)根据体育类人数除以体育类所占的百分比,可得被调查的学生人数,再求出喜欢“科普书籍”的人数即可求出喜欢“科普书籍”出现的频率;
(2)用乘以“科普书籍”所占的比例可得“科普书籍”所占的圆心角度数;
(3)用全校人数乘以最喜欢“文艺”书籍的所占的百分比可得答案.
【详解】(1)解:被调查的学生人数为:(人),
喜欢“科普书籍”的人数为(人),
喜欢“科普书籍”出现的频率为;
故答案为:;
(2)解:“科普书籍”所占的圆心角度数为:,
故答案为:;
(3)解:(人),
答:估计该校最喜欢“科普书籍”书籍的学生有人.
20.(1)见解析;
(2),,理由见解析.
【分析】本题考查了矩形的判定与性质,等腰三角形的性质,中位线的性质与判定,熟练掌握以上知识点是解题的关键;
(1)根据等腰三角形三线合一得到,,结合是的外角的平分线,可得出,又由即可得到,然后根据矩形的判断即可得证;
(2)利用矩形的性质可求,根据三角形中线可得,得出是的中位线,即可得出结论.
【详解】(1)证明:中,,是中线,
,,
,
为的外角的平分线,
,
,
即,
,
,
四边形是矩形;
(2)解:,,理由如下:
由(1)知,四边形为矩形,
,
中,是中线,
,
是的中位线,
,.
21.(1)见解析;
(2),理由见解析;
(3)
【分析】(1)证明是等腰直角三角形,利用即可证明,从而证得,据此即可证得结论;
(2)同(1)相同,利用即可证得,从而证得,即可得到;
(3)过点作,过点作,勾股定理求出的长,三线合一求出的长,进而求出的长,根据全等三角形的性质,求出的长,证明为等腰三角形,求出的长,进而求出的长,证明,求出的长,勾股定理求出的长即可.
【详解】(1)证明:∵,,
∴,
∴,
∵四边形是正方形,
∴,,
∵,,
∴,
则在和中,
,
∴
∴,
∵,
∴;
(2);
理由:∵,,
∴,
∴,
∵四边形是正方形,
∴,,
∵,,
∴,
∵在和中,
∴
∴,
∴,
∴;
(3)过点作,过点作,如图:
∵,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
由(2)知:,
∴,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
又∵,,
∴,
∴,,
∴,
∴.
【点睛】本题考查正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,熟练掌握相关知识点,添加辅助线构造全等三角形,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
