期中模拟训练 2024--2025学年初中数学人教版八年级下册
文档属性
| 名称 | 期中模拟训练 2024--2025学年初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中模拟训练
2024--2025学年初中数学人教版八年级下册
一、单选题
1.下列式子中,是二次根式的是( )
A. B. C. D.
2.下列各组线段中,可以构成直角三角形的是( )
A.1,5,6 B.2,3,4 C.5,12,13 D.1,,3
3.下列计算正确的是( )
A. B.
C. D.
4.在中,,,的对边分别记为a,b,c,下列条件不能够判定为直角三角形的是( )
A. B.
C.,, D.
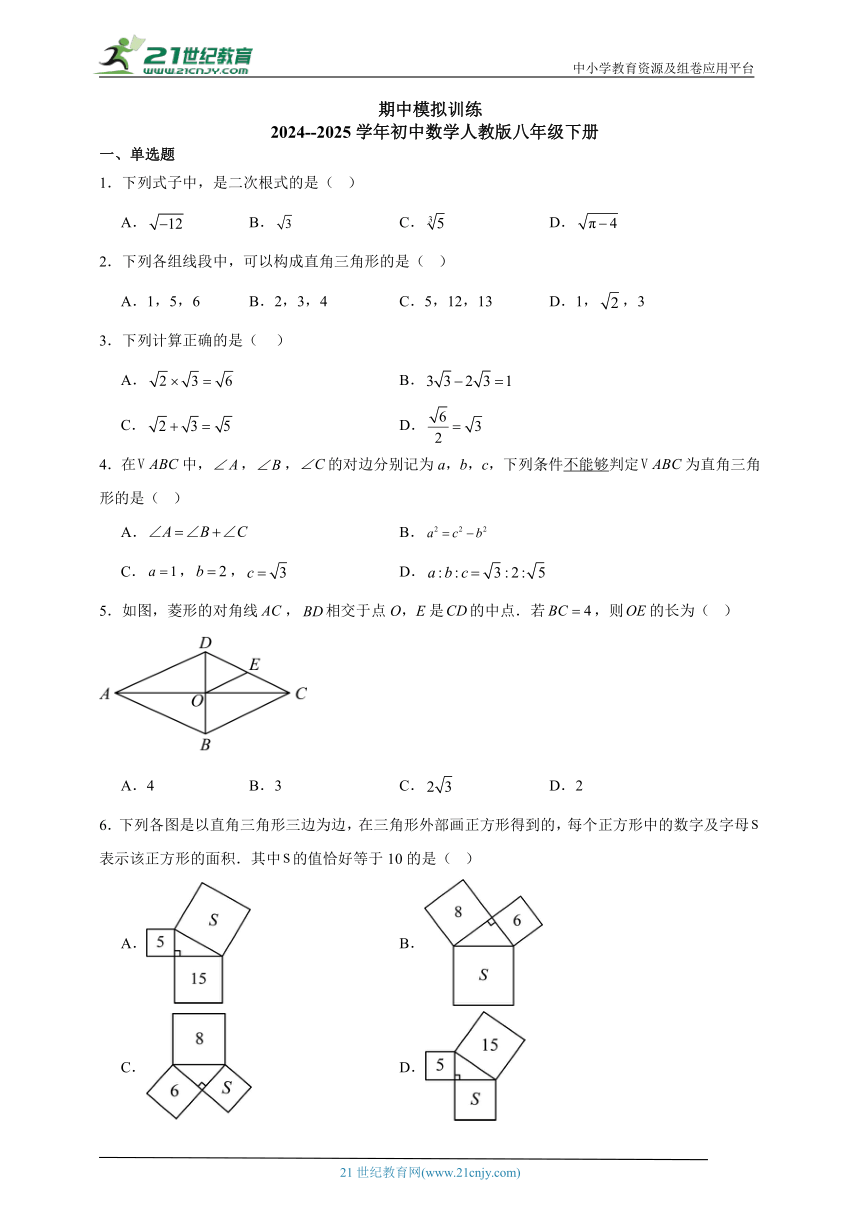
5.如图,菱形的对角线,相交于点O,E是的中点.若,则的长为( )
A.4 B.3 C. D.2
6.下列各图是以直角三角形三边为边,在三角形外部画正方形得到的,每个正方形中的数字及字母表示该正方形的面积.其中的值恰好等于10的是( )
A. B.
C. D.
7.如图,在平行四边形中,的平分线和的平分线交于上一点,若,,则的长为( )
A. B. C.5 D.6
8.如图,四边形是矩形,对角线相交于点O,过点O作的垂线分别交于点E和点F,点G是的中点,连接.若,则的度数为( ).
A. B. C. D.
9.如图(1)是一把折叠椅实物图,支架与交于点.如图(2)是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行,,折叠后椅子比完全打开时高( ).
A.42 B. C. D.
10.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为,则该三角形的面积为.现已知的三边长分别为,则面积为( )
A. B. C. D.
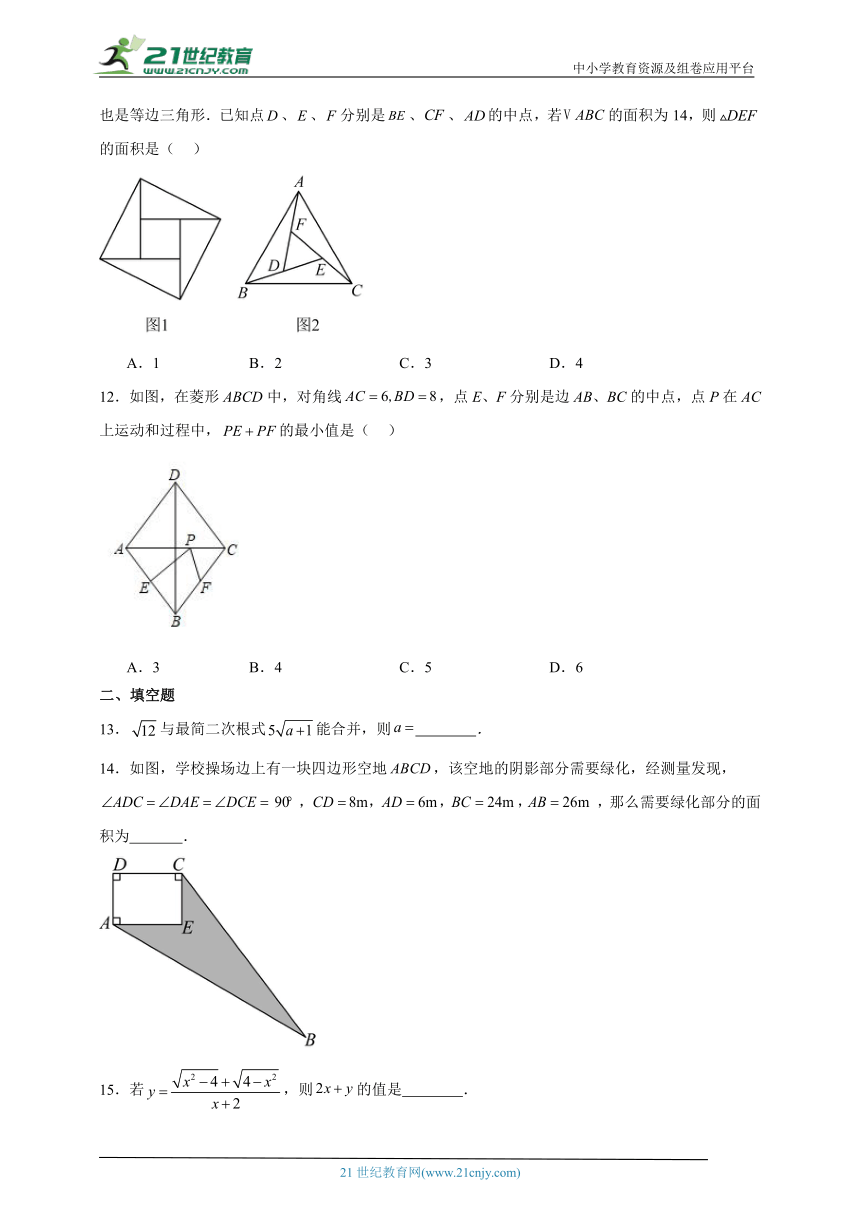
11.大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(如图1).某数学兴趣小组类比“赵爽弦图”构造出图2:为等边三角形,、、围成的也是等边三角形.已知点、、分别是、、的中点,若的面积为14,则的面积是( )
A.1 B.2 C.3 D.4
12.如图,在菱形ABCD中,对角线,点E、F分别是边AB、BC的中点,点P在AC上运动和过程中,的最小值是( )
A.3 B.4 C.5 D.6
二、填空题
13.与最简二次根式能合并,则 .
14.如图,学校操场边上有一块四边形空地,该空地的阴影部分需要绿化,经测量发现,,,那么需要绿化部分的面积为 .
15.若,则的值是 .
16.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,5尺人高曾记,仕女家人争蹴,良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,运用所学知识求出绳索的长是 尺.
17.如图,在平行四边形中,为上任意一点,若的面积为,的面积为,则的面积为 .
18.已知:如图,在正方形外取一点,连接,,.过点作的垂线交于点.若,.下列结论:
①;
②点到直线的距离为;
③;
④;
⑤,
其中正确结论的序号是 .
三、解答题
19.计算:
(1)
(2).
20.如图,□ABCD中,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:BF=DE;
(2)如果∠ABC=75°, ∠DBC=30°,BC=2,求BD的长.
21.如图,已知点是等边内一点,连结,,,D为外一点,且,连接,,.
(1)求证:.
(2)若,,,求的度数.
22.如图在△ABC中,∠CAB=,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线,交BE的延长线于点F,连接CF,
(1)试判断四边形ADCF的形状,并说明理由.
(2)若四边形ADCF是正方形,BF与AE有什么数量关系?说明理由.
(3)若AC=6,AB=8,求BF的长.
23.已知,如图,在矩形中,,.延长到点,使,连接.
(1)动点从点出发,以每秒1个单位的速度沿向终点运动,设点运动的时间为秒,当的值为__________时,以、、为顶点的三角形和全等;
(2)若动点从点出发,以每秒1个单位的速度仅沿着向终点运动,连接.设点运动的时间为秒,是否存在,使为等腰三角形?若存在,请求出的值;若不存在,说明理由.
24.如图,在中,点O为线段的中点,延长交的延长线于点E,连接,.
(1)求证:四边形是矩形;
(2)连接.若,求的长.
25.如图,四边形中,,使,,于点E,且.
(1)求的长.
(2)若动点P从点D出发,速度为2个单位/秒,沿向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿向点C运动,当一个动点到达端点时,另一个动点同时停止运动.设运动时间为t秒.
当t= 秒时,四边形是矩形.
当t为何值时,线段与四边形的边构成平行四边形?
参考答案
1.B
本题考查了二次根式的定义,一般形如的形式叫做二次根式,掌握二次根式的定义是解题的键.据此逐项判断即可.
解:A、中,不是二次根式,不符合题意;
B、是二次根式,符合题意;
C、不是二次根式,不符合题意;
D、中,不是二次根式,不符合题意;
故选:B.
2.C
本题考查了勾股定理的逆定理,根据勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解:A、,不能构成三角形,故不是直角三角形;
B、,故不是直角三角形;
C、,是直角三角形;
D、,故不是直角三角形;
故选:C.
3.A
本题考查了二次根式的运算,解题的关键是掌握二次根式的加减乘除运算法则.
分别根据二次根式的乘法,减法,加法,除法法则对每个选项进行分析判断.
A、根据二次根式乘法法则,则,该选项正确.
B、根据二次根式减法法则, ,该选项错误.
C、与不是同类二次根式,不能直接相加,即,该选项错误.
D、,该选项错误.
故选:A.
4.D
本题考查三角形的内角和,勾股定理逆定理,能够熟练掌握勾股定理是解决本题的关键.根据三角形的内角和等于,各个角之间的数量关系,计算各个角的度数,根据边之间的等量关系,结合勾股定理来判断各个选项是否符合题意.
解:A.∵,,∴,∴能判定为直角三角形;
B.∵,∴,∴能判定为直角三角形;
C.∵,∴,∴能判定为直角三角形;
D.∵,∴,∴不能判定为直角三角形.
故选D.
5.D
本题考查了菱形的性质,三角形的中位线的性质,由菱形的性质可得,由三角形中位线的性质可得,故可求解.
解:∵四边形是菱形,
∴,,
∵点E是的中点,,
∴,
故选:D.
6.D
本题主要考查了勾股定理的应用,
根据勾股定理可知以直角三角形的三边为边长分别作三个正方形,两个正方形的面积和等于最大正方形的面积,逐个判断答案即可.
解:因为,所以A不符合题意;
因为,所以B不符合题意;
因为,所以C不符合题意;
因为,所以D符合题意.
故选:D.
7.B
本题考查了平行四边形的性质,平行线的性质,等角对等边,勾股定理,熟练掌握以上知识点是解题的关键.根据角平分线可知,,,结合四边形是平行四边形,,,从而得到,,,最后在中利用勾股定理即可求解.
解:四边形是平行四边形,
,,,
,,
的平分线和的平分线交于上一点
,
,,
,
故选:B.
8.D
本题考查了直角三角形斜边上中线等于斜边一半,等腰三角形的性质,矩形的性质,根据直角三角形斜边上中线等于斜边一半得到,则可求出,即可解答,熟知上述性质是解题的关键.
解:四边形是矩形,
,
,
垂直平分,点G是的中点,
,
,
,
,
,
故选:D.
9.D
本题考查了勾股定理,平行线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为点,从而可得,再利用平行线的性质可得,从而可得是等边三角形,然后利用等边三角形的性质可得,,再根据平行线的性质可得:,从而可得,进而可得,最后根据等边三角形的判定可得:是等边三角形,从而可得,再利用直角三角形的两个锐角互余可得:,从而中,利用含30度角的直角三角形性质可得,再利用勾股定理求出的长,从而进行计算即可解答.
解:过点作,垂足为点,
,
,
,
,
是等边三角形,
,,
,
,
,
,
,
,
是等边三角形,
,
,
,,
,
,
,
,
折叠后椅子比完全打开时高,
故选:D.
10.B
本题考查了二次根式的应用,熟练掌握运算法则是解题的关键.把代入计算即可.
解:,
,
,
故选:B.
11.B
连接,由题意知,再由点、、分别是、、的中点,可得,,即可得出即可求解.
解:连接,如图所示:
点、、分别是、、的中点,
,,
为等边三角形,也是等边三角形,
,
,
是的一个外角,
,
是的一个外角,
,
,
在和中,
,
,
同理,可得,
,
,
,
,
,解得,
故选:B.
本题考查求三角形面积,涉及等边三角形的性质,中点性质,全等三角形的判定与性质,三角形外角性质,正确作出辅助线,得出是解题的关键.
12.C
设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,可得此时EP+FP的值最小,最小值为NF,再由菱形的性质证得四边形ANFB是平行四边形,然后根据勾股定理求出AB,即可求解.
解:设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,
∴PN=PE,
∴PE+PF=PN+PF,
∴此时EP+FP的值最小,最小值为NF,
∵四边形ABCD是菱形,
∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,,
∵E为AB的中点,
∴N在AD上,且N为AD的中点,
∵,
∴∠ANP=∠CFP,∠NAP=∠FCP,
∵AD=BC,N为AD中点,F为BC中点,
∴AN=CF,
∴,
∴AP=CP,
即P为AC中点,
∵O为AC中点,
∴P、O重合, 即NF过O点,
∵,AN=BF,
∴四边形ANFB是平行四边形,
∴NF=AB,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=3,BO=BD=4,
由勾股定理得:AB=5,即NF=5,
∴的最小值是5.
故选:C
本题主要考查了菱形的性质,勾股定理,平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握菱形的性质,勾股定理,平行四边形的判定和性质,全等三角形的判定和性质是解题的关键.
13.
本题考查了同类二次根式,掌握同类二次根式的定义是解题的关键.
能合并就是同类二次根式,都化成最简二次根式后被开方数相同,据此求解即可.
解:,
与最简二次根式能合并,
,
解得: ,
故答案为: .
14./96平方米
本题考查勾股定理及其逆定理.根据勾股定理,求得,根据勾股定理逆定理,可判定是直角三角形,.
解:连接,
∵,
∴四边形是矩形,
∴,
中,;
∵,
∴,
∴.
故答案为:
15.4
根据二次根式的被开方数是非负数,可以得到,再根据分母不能为0确定出x的值,从而得到y的值,代入即可.本题主要考查了二次根式的非负性及分式有意义的条件当时由意义,分式的分母不为0时分式有意义,熟练掌握以上知识是解题的关键.
解: ,且,
,且,
,
,
又,
,
,
,
.
故答案为:4
16.
本题主要考查了勾股定理的应用,明确题意,列出方程是解题的关键.设绳索的长为x尺,根据题意知,可列出关于 的方程,即可求解.
解:由题意可知:尺,尺,
∴(尺),
设绳索尺,
根据题意得:,
解得.
答:绳索的长为尺.
故答案为:.
17.
本题考查平行四边形的知识,解题的关键是掌握平行四边形的性质,则,,过点作交于点,根据,,则,根据,即可.
过点作交于点,
∵四边形是平行四边形,
∴,,
∵为上任意一点,
∴,
∵的面积为,的面积为,
∴,,
∴,
∵,
∴,
故答案为:.
18.①②③④
①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;
③利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;
②过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;
④在Rt△ABF中,利用勾股定理可求AB2,即是正方形的面积;
⑤连接BD,求出△ABD的面积,然后减去△BDP的面积即可.
解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∴△APD≌△AEB(SAS);
故此选项成立;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;
故此选项成立;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=,
∴BF=EF=BE=;
故此选项成立;
④∵EF=BF=,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=,
∴S正方形ABCD=AB2=;
故此选项成立;
⑤如图,连接BD,在Rt△AEP中,
∵AE=AP=1,
∴EP=,
又∵PB=,
∴BE=,
∵△APD≌△AEB,
∴PD=BE=,
∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣.
故此选项不成立;
综上可知其中正确结论的序号是①②③④.
故答案为:①②③④.
本题考查了全等三角形的判定和性质的运用、正方形的性质的运用、正方形和三角形的面积公式的运用、勾股定理的运用等知识.
19.(1)
(2)
此题考查了实数的混合运算和二次根式的混合运算.
(1)利用负整数指数幂、零指数幂、二次根式的加减法计算即可;
(2)利用积的乘方和完全平方公式计算,再用二次根式加减法计算即可.
(1)解:
(2)
20.(1)证明见解析;(2) +1.
(1)根据矩形的性质和已知条件证得△ADE≌△CBF,再利用全等三角形的性质即可证明;
(2)先根据矩形的性质、勾股定理等知识求得AE的长,进而求得DE和BD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠CBF.
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AED=∠CFB=90°.
在△ADE和△CBF中,
∠AED=∠BFC,∠ADE=∠CBF,AD=BC,
∴△ADE≌△CBF(AAS).
∴DE=BF.
(2)解:∵∠ABC=75°,∠DBC=30°,
∴∠ABE=75°-30°=45°.
∵AB∥CD,
∴∠ABE=∠BDC=45°,
∵AD=BC=2, ∠ADE=∠CBF=30°,
∴在Rt△ADE中,AE=1,DE==.
在Rt△AEB中,∠ABE=∠BAE=45°.
故AE=BE=1,则BD= +1.
本题主要考查了平行四边形的性质、全等三角形的判定与性质、勾股定理等知识,弄清题意、证得△ADE≌△CBF是解答本题关键.
21.(1)见解析
(2)
本题考查了全等三角形的判定和性质,等边三角形的判定和性质,勾股定理的逆定理.
(1)根据等边三角形的性质得到,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到,,推出是等边三角形,得到,,根据勾股定理的逆定理得到,于是得到结论.
(1)证明:∵是等边三角形,
∴,,
∵,,
∴是等边三角形,
∴,
∴,
在与中,
∴(SAS);
(2)解:∵,
∴,,
∵,
∵,
∴是等边三角形,
∴,,
∵,
∴,
∴,
∴.
22.(1)四边形ADCF是菱形,理由见解析.
(2)BF=,理由见解析.
(3)BF=
(1)由直角三角形斜边上的中线等于斜边的一半得AD=CD=BD,证明△AEF≌△DEB,则AF=BD,则AF=CD.又由于AFCD,因此四边形ADCF是平行四边形,又因AD=CD,因此四边形ADCF是菱形.
(2)由正方形的性质可得FC=CD=AD,由(1)知AD=DB,则FC=CD=DB,则CB=2FC.根据勾股定理可得BF=CF,又因为CF=AD=2AE,因此BF=.
(3)连接FD交AC于O点,作FG垂直于BA的延长线于D点,先证明四边形OFGA是矩形,则FG=OA==3,GA=OF=OD.由中位线的性质得OD==4,则GA=4,GB=12,根据勾股定理可求得BF的长.
(1)∵△ABC中,∠CAB=90 ,AD是BC边中线,
∴AD=CD=DB.
∵E是AD的中点,
∴AE=DE.
∵AFBC,
∴ ∠EFA=∠EBD.
又∵∠FEA=∠BED,
∴△AEF≌△DEB(AAS),
∴AF=DB,
∴AF=CD.
∵AFCD,
∴四边形ADCF是平行四边形.
又∵AD=CD,
∴四边形ADCF是菱形.
(2)BF=,理由如下:
∵四边形ADCF是正方形,
∴FC=CD=AD,∠FCD=90°.
又∵AD=DB,
∴FC=CD=DB,
∴BC=2CF,
∴BF===,
,
∵AD=2AE,
∴BF==,
(3)
如图,连接FD交AC于O点,延长BA,过F点作FG垂直于BA的延长线于G点,
∵四边形ADCF是菱形,
∴∠AOF=90 .
∵∠CAB=90 ,
∴∠CAG=90 .
又∵FG丄AG,
∴∠G=90 ,
∴四边形OFGA是矩形,
∴FG=OA,GA=FO.
∵AC=6,O是AC的中点,
∴AO=3,
∴FG=3.
∵O点、D点是AC、BC的中点,
∴OD==4,
∴GA=OF=OD=4,
∴GB=4+8=12,
∴BF=.
本题是一道有关四边形的综合性题目,考查了直角三角形的性质,菱形的判定,正方形的性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质.熟练掌握以上知识是解题的关键.
23.(1)3或13;
(2)当或4或时,为等腰三角形.
本题考查的是全等三角形的判定与性质,等腰三角形的定义,勾股定理的应用,清晰的分类讨论是解本题的关键;
(1)分两种情况讨论:此和为对应边时,如图,当和为对应边时,再利用全等三角形的性质可得答案;
(2)先利用勾股定理求解,再分三种情况讨论即可.
(1)解:如图:
此和为对应边时,≌,有,
此时;
如图,当和为对应边时,则,
点运动的距离为,
此时,
故t的值为3或13.
故答案为:3或13.
(2)如图,连接,
四边形是矩形,
,,,
在中,,
,
若为等腰三角形,
则或或,
当时,
,,
,
,
,
当时,
,
,
,
当时,
,
,
在中,.
,
,
,
,
,
综上所述:当或4或时,为等腰三角形.
24.(1)见解析
(2)
()证,得,再证四边形是平行四边形,然后证,即可得出结论;
()过点作于点,由矩形的性质得,,再由等腰三角形的性质得,则为的中位线,得,然后由平行四边形的性质得,进而由勾股定理即可得出结论.
(1)证明:∵为的中点,
∴,
∵四边形是平行四边形,
∴,
∴,
又∵,
∴,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:如图,过点作于点,
∵四边形是矩形,
∴,,,,
∴,
∵,
∴,
∴为的中位线,
∴,
∵四边形是平行四边形,
∴,
∴,
在中,由勾股定理得:,
即的长为.
本题考查了平行四边形的判定和性质,矩形的判定和性质,全等三角形的判定和性质,三角形中位线定理以及勾股定理,熟练掌握相关判定定理和性质定理是解题的关键.
25.(1)
(2);或
(1)先在中求出的长,进而可求出的长.
(2)先画图,由于四边形是矩形,那么矩形的对边相等,于是,再根据路程速度时间,可得,进而可求出t;有两种情况,1)线段与构成平行四边形,2)线段与构成平行四边形,根据平行四边形的性质列出式子,进而可求出t.
(1)解:,
,
又, ,
,
,,
四边形是等腰梯形,
;
(2)设运动时间为t时,四边形是矩形,如图,
四边形是矩形,
,
,
解得,
故答案为:;
有两种情况:
1) 设运动时间为t时,线段与构成平行四边形,如图,
四边形是平行四边形,
,
,
解得;
2) 设运动时间为t时,线段与构成平行四边形,如图,
四边形是平行四边形,
,
,
解得;
综上所述,当或时,线段与四边形的边构成平行四边形.
本题考查了矩形的性质、平行四边形的性质、等腰梯形的性质,解题的关键是画出相关的图,根据图找出等量关系,进而求出t.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中模拟训练
2024--2025学年初中数学人教版八年级下册
一、单选题
1.下列式子中,是二次根式的是( )
A. B. C. D.
2.下列各组线段中,可以构成直角三角形的是( )
A.1,5,6 B.2,3,4 C.5,12,13 D.1,,3
3.下列计算正确的是( )
A. B.
C. D.
4.在中,,,的对边分别记为a,b,c,下列条件不能够判定为直角三角形的是( )
A. B.
C.,, D.
5.如图,菱形的对角线,相交于点O,E是的中点.若,则的长为( )
A.4 B.3 C. D.2
6.下列各图是以直角三角形三边为边,在三角形外部画正方形得到的,每个正方形中的数字及字母表示该正方形的面积.其中的值恰好等于10的是( )
A. B.
C. D.
7.如图,在平行四边形中,的平分线和的平分线交于上一点,若,,则的长为( )
A. B. C.5 D.6
8.如图,四边形是矩形,对角线相交于点O,过点O作的垂线分别交于点E和点F,点G是的中点,连接.若,则的度数为( ).
A. B. C. D.
9.如图(1)是一把折叠椅实物图,支架与交于点.如图(2)是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行,,折叠后椅子比完全打开时高( ).
A.42 B. C. D.
10.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为,则该三角形的面积为.现已知的三边长分别为,则面积为( )
A. B. C. D.
11.大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(如图1).某数学兴趣小组类比“赵爽弦图”构造出图2:为等边三角形,、、围成的也是等边三角形.已知点、、分别是、、的中点,若的面积为14,则的面积是( )
A.1 B.2 C.3 D.4
12.如图,在菱形ABCD中,对角线,点E、F分别是边AB、BC的中点,点P在AC上运动和过程中,的最小值是( )
A.3 B.4 C.5 D.6
二、填空题
13.与最简二次根式能合并,则 .
14.如图,学校操场边上有一块四边形空地,该空地的阴影部分需要绿化,经测量发现,,,那么需要绿化部分的面积为 .
15.若,则的值是 .
16.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,5尺人高曾记,仕女家人争蹴,良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,运用所学知识求出绳索的长是 尺.
17.如图,在平行四边形中,为上任意一点,若的面积为,的面积为,则的面积为 .
18.已知:如图,在正方形外取一点,连接,,.过点作的垂线交于点.若,.下列结论:
①;
②点到直线的距离为;
③;
④;
⑤,
其中正确结论的序号是 .
三、解答题
19.计算:
(1)
(2).
20.如图,□ABCD中,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:BF=DE;
(2)如果∠ABC=75°, ∠DBC=30°,BC=2,求BD的长.
21.如图,已知点是等边内一点,连结,,,D为外一点,且,连接,,.
(1)求证:.
(2)若,,,求的度数.
22.如图在△ABC中,∠CAB=,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线,交BE的延长线于点F,连接CF,
(1)试判断四边形ADCF的形状,并说明理由.
(2)若四边形ADCF是正方形,BF与AE有什么数量关系?说明理由.
(3)若AC=6,AB=8,求BF的长.
23.已知,如图,在矩形中,,.延长到点,使,连接.
(1)动点从点出发,以每秒1个单位的速度沿向终点运动,设点运动的时间为秒,当的值为__________时,以、、为顶点的三角形和全等;
(2)若动点从点出发,以每秒1个单位的速度仅沿着向终点运动,连接.设点运动的时间为秒,是否存在,使为等腰三角形?若存在,请求出的值;若不存在,说明理由.
24.如图,在中,点O为线段的中点,延长交的延长线于点E,连接,.
(1)求证:四边形是矩形;
(2)连接.若,求的长.
25.如图,四边形中,,使,,于点E,且.
(1)求的长.
(2)若动点P从点D出发,速度为2个单位/秒,沿向点A运动,同时,动点Q从点B出发,速度为3个单位/秒,沿向点C运动,当一个动点到达端点时,另一个动点同时停止运动.设运动时间为t秒.
当t= 秒时,四边形是矩形.
当t为何值时,线段与四边形的边构成平行四边形?
参考答案
1.B
本题考查了二次根式的定义,一般形如的形式叫做二次根式,掌握二次根式的定义是解题的键.据此逐项判断即可.
解:A、中,不是二次根式,不符合题意;
B、是二次根式,符合题意;
C、不是二次根式,不符合题意;
D、中,不是二次根式,不符合题意;
故选:B.
2.C
本题考查了勾股定理的逆定理,根据勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解:A、,不能构成三角形,故不是直角三角形;
B、,故不是直角三角形;
C、,是直角三角形;
D、,故不是直角三角形;
故选:C.
3.A
本题考查了二次根式的运算,解题的关键是掌握二次根式的加减乘除运算法则.
分别根据二次根式的乘法,减法,加法,除法法则对每个选项进行分析判断.
A、根据二次根式乘法法则,则,该选项正确.
B、根据二次根式减法法则, ,该选项错误.
C、与不是同类二次根式,不能直接相加,即,该选项错误.
D、,该选项错误.
故选:A.
4.D
本题考查三角形的内角和,勾股定理逆定理,能够熟练掌握勾股定理是解决本题的关键.根据三角形的内角和等于,各个角之间的数量关系,计算各个角的度数,根据边之间的等量关系,结合勾股定理来判断各个选项是否符合题意.
解:A.∵,,∴,∴能判定为直角三角形;
B.∵,∴,∴能判定为直角三角形;
C.∵,∴,∴能判定为直角三角形;
D.∵,∴,∴不能判定为直角三角形.
故选D.
5.D
本题考查了菱形的性质,三角形的中位线的性质,由菱形的性质可得,由三角形中位线的性质可得,故可求解.
解:∵四边形是菱形,
∴,,
∵点E是的中点,,
∴,
故选:D.
6.D
本题主要考查了勾股定理的应用,
根据勾股定理可知以直角三角形的三边为边长分别作三个正方形,两个正方形的面积和等于最大正方形的面积,逐个判断答案即可.
解:因为,所以A不符合题意;
因为,所以B不符合题意;
因为,所以C不符合题意;
因为,所以D符合题意.
故选:D.
7.B
本题考查了平行四边形的性质,平行线的性质,等角对等边,勾股定理,熟练掌握以上知识点是解题的关键.根据角平分线可知,,,结合四边形是平行四边形,,,从而得到,,,最后在中利用勾股定理即可求解.
解:四边形是平行四边形,
,,,
,,
的平分线和的平分线交于上一点
,
,,
,
故选:B.
8.D
本题考查了直角三角形斜边上中线等于斜边一半,等腰三角形的性质,矩形的性质,根据直角三角形斜边上中线等于斜边一半得到,则可求出,即可解答,熟知上述性质是解题的关键.
解:四边形是矩形,
,
,
垂直平分,点G是的中点,
,
,
,
,
,
故选:D.
9.D
本题考查了勾股定理,平行线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为点,从而可得,再利用平行线的性质可得,从而可得是等边三角形,然后利用等边三角形的性质可得,,再根据平行线的性质可得:,从而可得,进而可得,最后根据等边三角形的判定可得:是等边三角形,从而可得,再利用直角三角形的两个锐角互余可得:,从而中,利用含30度角的直角三角形性质可得,再利用勾股定理求出的长,从而进行计算即可解答.
解:过点作,垂足为点,
,
,
,
,
是等边三角形,
,,
,
,
,
,
,
,
是等边三角形,
,
,
,,
,
,
,
,
折叠后椅子比完全打开时高,
故选:D.
10.B
本题考查了二次根式的应用,熟练掌握运算法则是解题的关键.把代入计算即可.
解:,
,
,
故选:B.
11.B
连接,由题意知,再由点、、分别是、、的中点,可得,,即可得出即可求解.
解:连接,如图所示:
点、、分别是、、的中点,
,,
为等边三角形,也是等边三角形,
,
,
是的一个外角,
,
是的一个外角,
,
,
在和中,
,
,
同理,可得,
,
,
,
,
,解得,
故选:B.
本题考查求三角形面积,涉及等边三角形的性质,中点性质,全等三角形的判定与性质,三角形外角性质,正确作出辅助线,得出是解题的关键.
12.C
设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,可得此时EP+FP的值最小,最小值为NF,再由菱形的性质证得四边形ANFB是平行四边形,然后根据勾股定理求出AB,即可求解.
解:设AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,
∴PN=PE,
∴PE+PF=PN+PF,
∴此时EP+FP的值最小,最小值为NF,
∵四边形ABCD是菱形,
∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,,
∵E为AB的中点,
∴N在AD上,且N为AD的中点,
∵,
∴∠ANP=∠CFP,∠NAP=∠FCP,
∵AD=BC,N为AD中点,F为BC中点,
∴AN=CF,
∴,
∴AP=CP,
即P为AC中点,
∵O为AC中点,
∴P、O重合, 即NF过O点,
∵,AN=BF,
∴四边形ANFB是平行四边形,
∴NF=AB,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=3,BO=BD=4,
由勾股定理得:AB=5,即NF=5,
∴的最小值是5.
故选:C
本题主要考查了菱形的性质,勾股定理,平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握菱形的性质,勾股定理,平行四边形的判定和性质,全等三角形的判定和性质是解题的关键.
13.
本题考查了同类二次根式,掌握同类二次根式的定义是解题的关键.
能合并就是同类二次根式,都化成最简二次根式后被开方数相同,据此求解即可.
解:,
与最简二次根式能合并,
,
解得: ,
故答案为: .
14./96平方米
本题考查勾股定理及其逆定理.根据勾股定理,求得,根据勾股定理逆定理,可判定是直角三角形,.
解:连接,
∵,
∴四边形是矩形,
∴,
中,;
∵,
∴,
∴.
故答案为:
15.4
根据二次根式的被开方数是非负数,可以得到,再根据分母不能为0确定出x的值,从而得到y的值,代入即可.本题主要考查了二次根式的非负性及分式有意义的条件当时由意义,分式的分母不为0时分式有意义,熟练掌握以上知识是解题的关键.
解: ,且,
,且,
,
,
又,
,
,
,
.
故答案为:4
16.
本题主要考查了勾股定理的应用,明确题意,列出方程是解题的关键.设绳索的长为x尺,根据题意知,可列出关于 的方程,即可求解.
解:由题意可知:尺,尺,
∴(尺),
设绳索尺,
根据题意得:,
解得.
答:绳索的长为尺.
故答案为:.
17.
本题考查平行四边形的知识,解题的关键是掌握平行四边形的性质,则,,过点作交于点,根据,,则,根据,即可.
过点作交于点,
∵四边形是平行四边形,
∴,,
∵为上任意一点,
∴,
∵的面积为,的面积为,
∴,,
∴,
∵,
∴,
故答案为:.
18.①②③④
①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;
③利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;
②过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;
④在Rt△ABF中,利用勾股定理可求AB2,即是正方形的面积;
⑤连接BD,求出△ABD的面积,然后减去△BDP的面积即可.
解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∴△APD≌△AEB(SAS);
故此选项成立;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;
故此选项成立;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=,
∴BF=EF=BE=;
故此选项成立;
④∵EF=BF=,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=,
∴S正方形ABCD=AB2=;
故此选项成立;
⑤如图,连接BD,在Rt△AEP中,
∵AE=AP=1,
∴EP=,
又∵PB=,
∴BE=,
∵△APD≌△AEB,
∴PD=BE=,
∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣.
故此选项不成立;
综上可知其中正确结论的序号是①②③④.
故答案为:①②③④.
本题考查了全等三角形的判定和性质的运用、正方形的性质的运用、正方形和三角形的面积公式的运用、勾股定理的运用等知识.
19.(1)
(2)
此题考查了实数的混合运算和二次根式的混合运算.
(1)利用负整数指数幂、零指数幂、二次根式的加减法计算即可;
(2)利用积的乘方和完全平方公式计算,再用二次根式加减法计算即可.
(1)解:
(2)
20.(1)证明见解析;(2) +1.
(1)根据矩形的性质和已知条件证得△ADE≌△CBF,再利用全等三角形的性质即可证明;
(2)先根据矩形的性质、勾股定理等知识求得AE的长,进而求得DE和BD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠CBF.
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AED=∠CFB=90°.
在△ADE和△CBF中,
∠AED=∠BFC,∠ADE=∠CBF,AD=BC,
∴△ADE≌△CBF(AAS).
∴DE=BF.
(2)解:∵∠ABC=75°,∠DBC=30°,
∴∠ABE=75°-30°=45°.
∵AB∥CD,
∴∠ABE=∠BDC=45°,
∵AD=BC=2, ∠ADE=∠CBF=30°,
∴在Rt△ADE中,AE=1,DE==.
在Rt△AEB中,∠ABE=∠BAE=45°.
故AE=BE=1,则BD= +1.
本题主要考查了平行四边形的性质、全等三角形的判定与性质、勾股定理等知识,弄清题意、证得△ADE≌△CBF是解答本题关键.
21.(1)见解析
(2)
本题考查了全等三角形的判定和性质,等边三角形的判定和性质,勾股定理的逆定理.
(1)根据等边三角形的性质得到,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到,,推出是等边三角形,得到,,根据勾股定理的逆定理得到,于是得到结论.
(1)证明:∵是等边三角形,
∴,,
∵,,
∴是等边三角形,
∴,
∴,
在与中,
∴(SAS);
(2)解:∵,
∴,,
∵,
∵,
∴是等边三角形,
∴,,
∵,
∴,
∴,
∴.
22.(1)四边形ADCF是菱形,理由见解析.
(2)BF=,理由见解析.
(3)BF=
(1)由直角三角形斜边上的中线等于斜边的一半得AD=CD=BD,证明△AEF≌△DEB,则AF=BD,则AF=CD.又由于AFCD,因此四边形ADCF是平行四边形,又因AD=CD,因此四边形ADCF是菱形.
(2)由正方形的性质可得FC=CD=AD,由(1)知AD=DB,则FC=CD=DB,则CB=2FC.根据勾股定理可得BF=CF,又因为CF=AD=2AE,因此BF=.
(3)连接FD交AC于O点,作FG垂直于BA的延长线于D点,先证明四边形OFGA是矩形,则FG=OA==3,GA=OF=OD.由中位线的性质得OD==4,则GA=4,GB=12,根据勾股定理可求得BF的长.
(1)∵△ABC中,∠CAB=90 ,AD是BC边中线,
∴AD=CD=DB.
∵E是AD的中点,
∴AE=DE.
∵AFBC,
∴ ∠EFA=∠EBD.
又∵∠FEA=∠BED,
∴△AEF≌△DEB(AAS),
∴AF=DB,
∴AF=CD.
∵AFCD,
∴四边形ADCF是平行四边形.
又∵AD=CD,
∴四边形ADCF是菱形.
(2)BF=,理由如下:
∵四边形ADCF是正方形,
∴FC=CD=AD,∠FCD=90°.
又∵AD=DB,
∴FC=CD=DB,
∴BC=2CF,
∴BF===,
,
∵AD=2AE,
∴BF==,
(3)
如图,连接FD交AC于O点,延长BA,过F点作FG垂直于BA的延长线于G点,
∵四边形ADCF是菱形,
∴∠AOF=90 .
∵∠CAB=90 ,
∴∠CAG=90 .
又∵FG丄AG,
∴∠G=90 ,
∴四边形OFGA是矩形,
∴FG=OA,GA=FO.
∵AC=6,O是AC的中点,
∴AO=3,
∴FG=3.
∵O点、D点是AC、BC的中点,
∴OD==4,
∴GA=OF=OD=4,
∴GB=4+8=12,
∴BF=.
本题是一道有关四边形的综合性题目,考查了直角三角形的性质,菱形的判定,正方形的性质,矩形的判定和性质,三角形中位线的性质,全等三角形的判定和性质.熟练掌握以上知识是解题的关键.
23.(1)3或13;
(2)当或4或时,为等腰三角形.
本题考查的是全等三角形的判定与性质,等腰三角形的定义,勾股定理的应用,清晰的分类讨论是解本题的关键;
(1)分两种情况讨论:此和为对应边时,如图,当和为对应边时,再利用全等三角形的性质可得答案;
(2)先利用勾股定理求解,再分三种情况讨论即可.
(1)解:如图:
此和为对应边时,≌,有,
此时;
如图,当和为对应边时,则,
点运动的距离为,
此时,
故t的值为3或13.
故答案为:3或13.
(2)如图,连接,
四边形是矩形,
,,,
在中,,
,
若为等腰三角形,
则或或,
当时,
,,
,
,
,
当时,
,
,
,
当时,
,
,
在中,.
,
,
,
,
,
综上所述:当或4或时,为等腰三角形.
24.(1)见解析
(2)
()证,得,再证四边形是平行四边形,然后证,即可得出结论;
()过点作于点,由矩形的性质得,,再由等腰三角形的性质得,则为的中位线,得,然后由平行四边形的性质得,进而由勾股定理即可得出结论.
(1)证明:∵为的中点,
∴,
∵四边形是平行四边形,
∴,
∴,
又∵,
∴,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:如图,过点作于点,
∵四边形是矩形,
∴,,,,
∴,
∵,
∴,
∴为的中位线,
∴,
∵四边形是平行四边形,
∴,
∴,
在中,由勾股定理得:,
即的长为.
本题考查了平行四边形的判定和性质,矩形的判定和性质,全等三角形的判定和性质,三角形中位线定理以及勾股定理,熟练掌握相关判定定理和性质定理是解题的关键.
25.(1)
(2);或
(1)先在中求出的长,进而可求出的长.
(2)先画图,由于四边形是矩形,那么矩形的对边相等,于是,再根据路程速度时间,可得,进而可求出t;有两种情况,1)线段与构成平行四边形,2)线段与构成平行四边形,根据平行四边形的性质列出式子,进而可求出t.
(1)解:,
,
又, ,
,
,,
四边形是等腰梯形,
;
(2)设运动时间为t时,四边形是矩形,如图,
四边形是矩形,
,
,
解得,
故答案为:;
有两种情况:
1) 设运动时间为t时,线段与构成平行四边形,如图,
四边形是平行四边形,
,
,
解得;
2) 设运动时间为t时,线段与构成平行四边形,如图,
四边形是平行四边形,
,
,
解得;
综上所述,当或时,线段与四边形的边构成平行四边形.
本题考查了矩形的性质、平行四边形的性质、等腰梯形的性质,解题的关键是画出相关的图,根据图找出等量关系,进而求出t.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
