18.1.2 平行四边形的判定 第1课时 同步练习 2024--2025学年初中数学人教版八年级下册
文档属性
| 名称 | 18.1.2 平行四边形的判定 第1课时 同步练习 2024--2025学年初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 863.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 16:44:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
18.1.2 平行四边形的判定 第1课时 同步练习
2024--2025学年初中数学人教版八年级下册
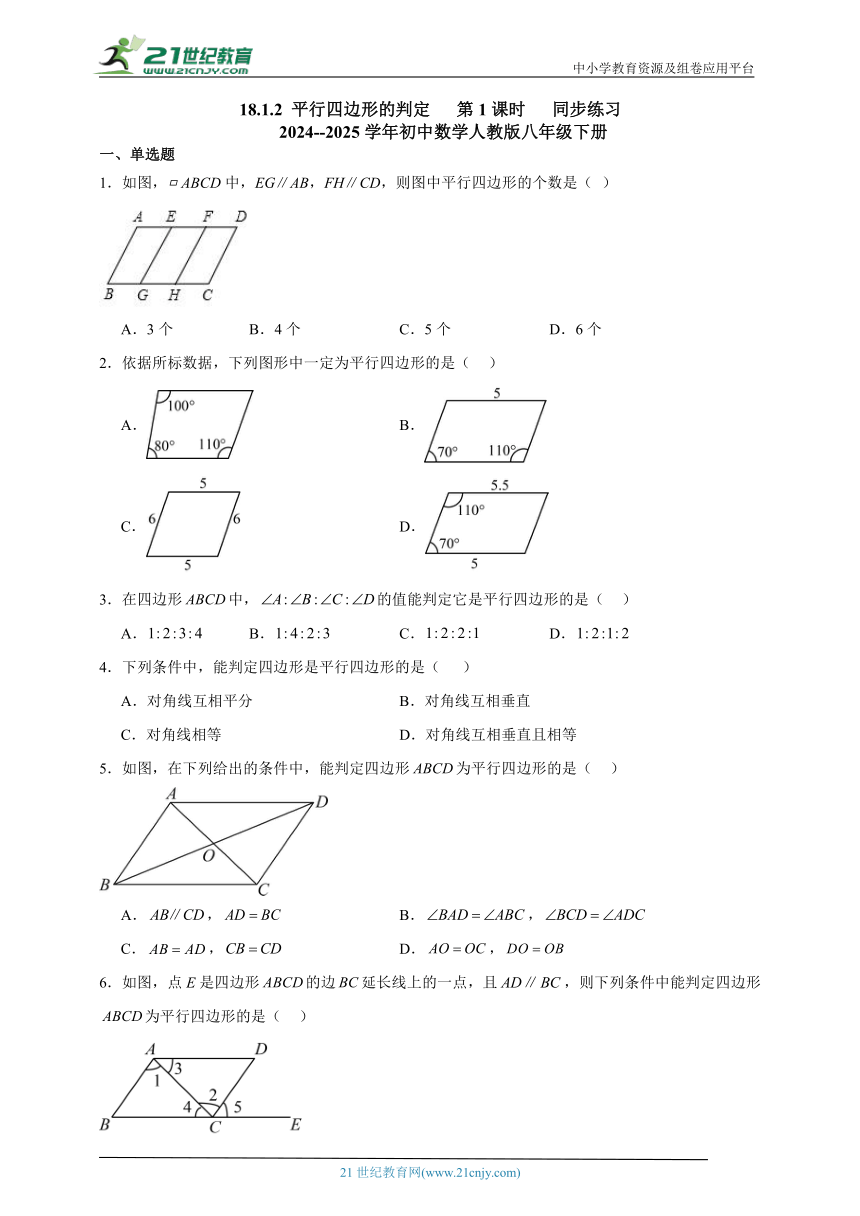
一、单选题
1.如图,ABCD中,EG∥AB,FH∥CD,则图中平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
2.依据所标数据,下列图形中一定为平行四边形的是( )
A. B.
C. D.
3.在四边形中,的值能判定它是平行四边形的是( )
A. B. C. D.
4.下列条件中,能判定四边形是平行四边形的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
5.如图,在下列给出的条件中,能判定四边形为平行四边形的是( )
A., B.,
C., D.,
6.如图,点E是四边形的边延长线上的一点,且,则下列条件中能判定四边形为平行四边形的是( )
A. B. C. D.
7.如图,在四边形中,,若,则的度数是( )
A. B. C. D.
8.如图,的对角线,相交于点,,,若,,则四边形的周长为( )
A.4 B.6 C.8 D.16
二、填空题
9.如图,DE∥BC,DF∥AC,EF∥AB,图中共有 个平行四边形.
10.在四边形中,AB∥CD,AD∥BC,、相交于点O,若,则线段的长度等于 .
11.如图,、是平行四边形的对角线上的点,要使四边形是平行四边形 (只需添加一个正确的即可).
12.如图,两条对边平行且宽为的纸条交叉重叠在一起,其中较小交叉角为,则重叠四边形的面积为 .
13.如图,在中,过对角线上一点P作,,且,,则 .
三、解答题
14.如图,在中,点,分别在边,上,.
(1)求证:;
(2)连接.请添加一个与线段相关的条件,使四边形是平行四边形.(不需要说明理由)
15.如图,在四边形中,
(1)证明:四边形是平行四边形;
(2)当时,求四边形的面积.
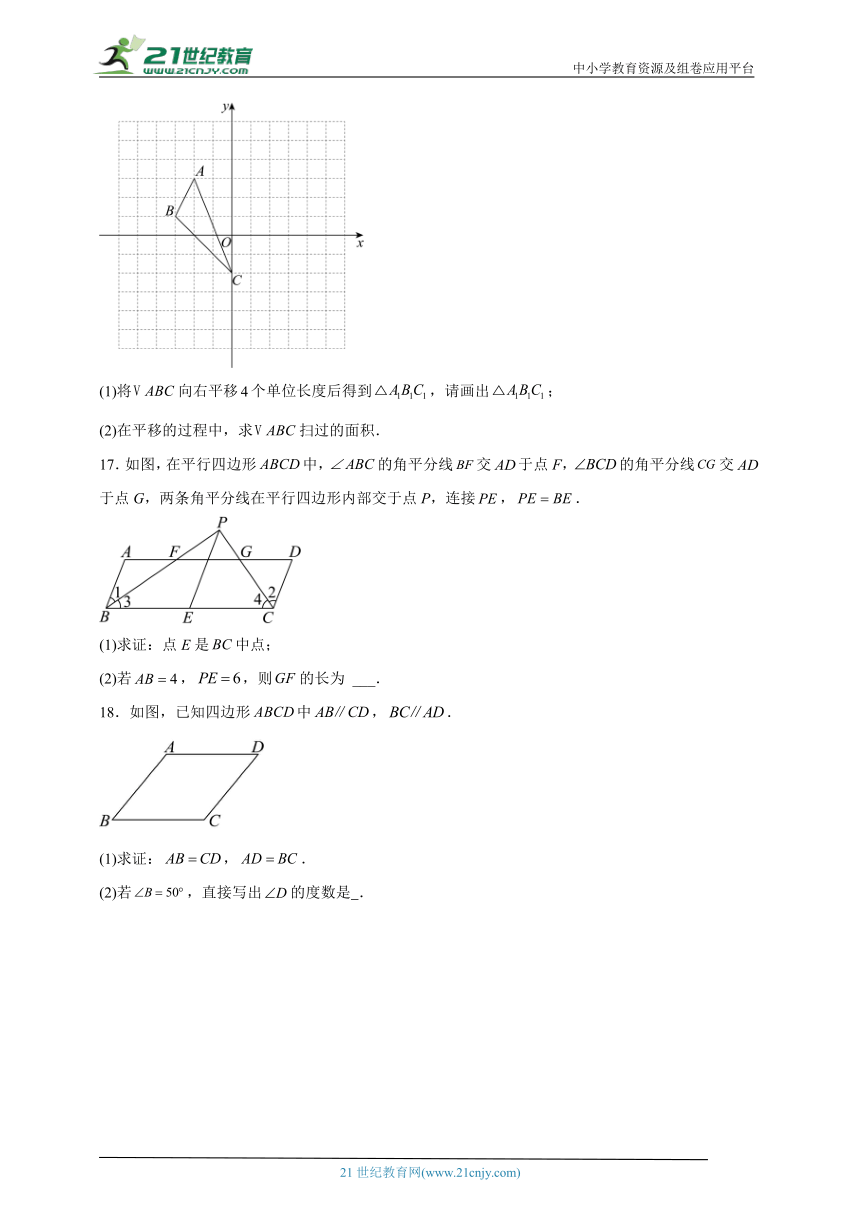
16.如图,在平面直角坐标系中,已知的三个顶点坐标分别为,,.
(1)将向右平移个单位长度后得到,请画出;
(2)在平移的过程中,求扫过的面积.
17.如图,在平行四边形中,的角平分线交于点F,的角平分线交于点G,两条角平分线在平行四边形内部交于点P,连接,.
(1)求证:点E是中点;
(2)若,,则的长为 ___.
18.如图,已知四边形中,.
(1)求证:,.
(2)若,直接写出的度数是 .
参考答案
1.D
首先根据已知条件找出图中的平行线段,然后根据两组对边分别平行的四边形是平行四边形,来判断图中平行四边形的个数.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
又∵EG∥AB,FH∥CD,
∴EG∥AB∥FH∥CD,
根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
可得图中平行四边形有:□ ABGE、□ABHF、□ABCD、□EGCD、□EGHF、□FHCD,共6个.
故选D.
本题考查平行四边形的判定与性质,解题的关键是根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,找出图中的平行四边形.
2.C
根据平行四边形的判定定理判断即可.
解:A.两组对角分别相等的四边形是平行四边形,因此图中的四边形不可能是平行四边形,故A错误;
B.一组对边平行不能判断四边形是平行四边形,故B错误;
C.两组对边相等能判断四边形是平行四边形,故C正确;
D.一组对边平行但不相等的四边形不是平行四边形,故D错误.
故选:C.
本题主要考查平行四边形的判定及性质,掌握平行四边形的判定及性质是解题的关键.
3.D
平行四边形两组对角分别相等,由此判断即可.
解:的值为时,,,不能判定是平行四边形,故A选项不合题意;
的值为时,,,不能判定是平行四边形,故B选项不合题意;
的值为时,,,不能判定是平行四边形,故C选项不合题意;
的值为时,,,能够判定是平行四边形,故D选项符合题意;
故选D.
本题考查平行四边形的判定,解题的关键是掌握平行四边形两组对角分别相等.
4.A
本题考查平行四边形的判定,根据平行四边形的判定方法一一判断即可.
解:A、对角线互相平分的四边形是平行四边形.正确.
B、对角线互相垂直的四边形不一定是平行四边形.错误.
C、对角线相等的四边形不一定是平行四边形.错误.
D、对角线互相垂直且相等的四边形不一定是平行四边形.错误.
故选:A.
5.D
根据平行四边形的判定定理分别进行分析即可.
解:A、不能判定四边形是平行四边形,故不符合题意;
B、不能判定四边形是平行四边形,故不符合题意;
C、不能判定四边形是平行四边形,故不符合题意;
D、根据对角线互相平分的四边形是平行四边形,能判定四边形是平行四边形,故符合题意
故选:D.
此题主要考查了平行四边形的判定,解题的关键是掌握平行四边形的判定定理.
6.D
选项A,B中的条件都只能证得,不能判定四边形是平行四边形.选项C中的条件,不能判定四边形是平行四边形.对于选项D提供两组对边分别平行,能判定四边形为平行四边形,本题考查了平行四边形的判定,正确掌握相关性质内容是解题的关键.
解:∵
∴
选项A不能判定四边形是平行四边形.
∵
∴
选项B不能判定四边形是平行四边形.
∵,
∴不能判定四边形ABCD是平行四边形.
选项C不能判定四边形是平行四边形.
∵,
∴.
又,
∴,
∴,
∴四边形是平行四边形
故选:D
7.B
本题考查了平行四边形的性质和判定,熟练掌握平行四边形的性质和判定是解题的关键.
证明四边形是平行四边形,根据平行四边形的性质即可得到结论.
解:∵,
∴四边形是平行四边形,
∵,
,
故选:B.
8.C
本题考查了平行四边形的判定与性质,熟练掌握知识点是解题的关键.
由四边形是平行四边形得到,,再证明四边形是平行四边形,则,即可求解周长.
解:∵四边形是平行四边形,
∴,,
∵,,
∴四边形是平行四边形,
∴,
∴周长为:,
故选:C.
9.3
图中的平行四边形有□ADFE,□BDEF,□CEDF,共三个,故答案为3.
10.
根据在四边形ABCD中,AB∥CD,AD∥BC,得出四边形ABCD是平行四边形,然后即可求解.
解:∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=7,
∴AO=AC=×7=.
故答案为:.
此题主要考查了平行四边形的判定与性质,得出四边形ABCD是平行四边形是解题关键.
11.(答案不唯一)
本题考查平行四边形的判定与性质,添加:,根据平行四边形的性质得,,继而得到,即可得证.掌握平行四边形的判定是解题的关键.
解:添加的一个条件为.理由如下:
∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形.
故答案为:(答案不唯一).
12.
本题考查了平行四边形的性质与判定,含度角的直角三角形的性质,由题意可得得,,cm,可证四边形是平行四边形,由直角三角形的性质可求的长,即可求解.
解:如图,过点A作于,过点作于,
由题意可得,,cm,
∴四边形是平行四边形,
∵,,
∴,
∴重叠四边形的面积(),
故答案为:.
13.2
本题主要考查平行四边形的判定和性质,由条件可证明四边形、为平行四边形,再利用面积的和差可证明,最后由等高四边形的条件即可得出答案.
解:∵,,
∴四边形、、、为平行四边形,
∴,
同理可得,,
∴,
即.
∵,,
∴;
故答案为:2.
14.(1)见解析
(2)添加(答案不唯一)
本题考查了平行四边形的性质与判定,全等三角形的判定;
(1)根据平行四边形的性质得出,,结合已知条件可得,即可证明;
(2)添加,依据一组对边平行且相等的四边形是平行四边形,即可求解.
(1)证明:∵四边形是平行四边形,
∴,,,
∵,
∴即,
在与中,
,
∴;
(2)添加(答案不唯一)
如图所示,连接.
∵四边形是平行四边形,
∴,即,
当时,四边形是平行四边形.
15.(1)见详解
(2)216
本题考查了平行四边的性质与判定,勾股定理,求平行四边的面积,正确掌握相关性质内容是解题的关键.
(1)先由平行线的性质得,因为得,则两组对应边互相平行的四边形是平行四边形,即可作答.
(2)运用勾股定理列式,,则,解出,再运算出,结合平行四边形的面积等于底乘高,即可作答.
(1)解:∵
∴
∵
∴
∴
∵
∴四边形是平行四边形;
(2)解:过点作
设
∵
∴在
在
则
解得
∴
则四边形的面积
16.(1)作图见解析
(2)平方单位
本题考查平移作图,三角形的面积和平行四边形的面积,
(1)分别将点、、向右平移个单位长度,得到点、、,然后顺次连接得到;
(2)根据扫过的面积等于平行四边形的面积三角形的面积解答即可;
解题的关键是掌握平移的性质,平行四边形的判定与性质.
(1)解:如图所示:即为所作;
(2)连接、,
∵将向右平移个单位长度后得到,点、的对应点分别为点、,
∴,,
∴四边形是平行四边形,
(平方单位),
∴扫过的面积为平方单位.
17.(1)见解析
(2)4
(1)根据平行四边形的性质得出,根据平行线的性质得出,根据角平分线的定义得出,根据等腰三角形的性质得出,根据余角的性质得出,根据等腰三角形的判定得出,即可证明结论;
(2)证明四边形为平行四边形,得出,求出,证明,,得出,,最后求出结果即可.
(1)证:∵平行四边形,
∴,
∴,
∵、分别平分和,
∴,
,
,
,
,
,
,
,
为的中点;
(2)解:根据解析(1)可知:,,
∴,
∴,
∵四边形为平行四边形,
∴,
∴四边形为平行四边形,
∴,
∴,
∵,
∴,,
∵,,
∴,,
∴,,
∴.
故答案为:4.
本题主要考查了平行四边形的判定和性质,等腰三角形的判定和性质,平行线的性质,角平分线定义,解题的关键是熟练掌握相关的判定和性质.
18.(1)证明见解析
(2)
本题考查了平行四边形的判定和性质,熟练掌握平行四边形的判定和性质是解题的关键;
(1)根据两组对边互相平行的四边形是平行四边形,即可得出结论;
(2)根据平行四边形的性质,平行四边形的对角相等即可解答.
(1)解:,,
四边形是平行四边形,
,;
(2)由(1)得四边形是平行四边形,
,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
18.1.2 平行四边形的判定 第1课时 同步练习
2024--2025学年初中数学人教版八年级下册
一、单选题
1.如图,ABCD中,EG∥AB,FH∥CD,则图中平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
2.依据所标数据,下列图形中一定为平行四边形的是( )
A. B.
C. D.
3.在四边形中,的值能判定它是平行四边形的是( )
A. B. C. D.
4.下列条件中,能判定四边形是平行四边形的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
5.如图,在下列给出的条件中,能判定四边形为平行四边形的是( )
A., B.,
C., D.,
6.如图,点E是四边形的边延长线上的一点,且,则下列条件中能判定四边形为平行四边形的是( )
A. B. C. D.
7.如图,在四边形中,,若,则的度数是( )
A. B. C. D.
8.如图,的对角线,相交于点,,,若,,则四边形的周长为( )
A.4 B.6 C.8 D.16
二、填空题
9.如图,DE∥BC,DF∥AC,EF∥AB,图中共有 个平行四边形.
10.在四边形中,AB∥CD,AD∥BC,、相交于点O,若,则线段的长度等于 .
11.如图,、是平行四边形的对角线上的点,要使四边形是平行四边形 (只需添加一个正确的即可).
12.如图,两条对边平行且宽为的纸条交叉重叠在一起,其中较小交叉角为,则重叠四边形的面积为 .
13.如图,在中,过对角线上一点P作,,且,,则 .
三、解答题
14.如图,在中,点,分别在边,上,.
(1)求证:;
(2)连接.请添加一个与线段相关的条件,使四边形是平行四边形.(不需要说明理由)
15.如图,在四边形中,
(1)证明:四边形是平行四边形;
(2)当时,求四边形的面积.
16.如图,在平面直角坐标系中,已知的三个顶点坐标分别为,,.
(1)将向右平移个单位长度后得到,请画出;
(2)在平移的过程中,求扫过的面积.
17.如图,在平行四边形中,的角平分线交于点F,的角平分线交于点G,两条角平分线在平行四边形内部交于点P,连接,.
(1)求证:点E是中点;
(2)若,,则的长为 ___.
18.如图,已知四边形中,.
(1)求证:,.
(2)若,直接写出的度数是 .
参考答案
1.D
首先根据已知条件找出图中的平行线段,然后根据两组对边分别平行的四边形是平行四边形,来判断图中平行四边形的个数.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,
又∵EG∥AB,FH∥CD,
∴EG∥AB∥FH∥CD,
根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
可得图中平行四边形有:□ ABGE、□ABHF、□ABCD、□EGCD、□EGHF、□FHCD,共6个.
故选D.
本题考查平行四边形的判定与性质,解题的关键是根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,找出图中的平行四边形.
2.C
根据平行四边形的判定定理判断即可.
解:A.两组对角分别相等的四边形是平行四边形,因此图中的四边形不可能是平行四边形,故A错误;
B.一组对边平行不能判断四边形是平行四边形,故B错误;
C.两组对边相等能判断四边形是平行四边形,故C正确;
D.一组对边平行但不相等的四边形不是平行四边形,故D错误.
故选:C.
本题主要考查平行四边形的判定及性质,掌握平行四边形的判定及性质是解题的关键.
3.D
平行四边形两组对角分别相等,由此判断即可.
解:的值为时,,,不能判定是平行四边形,故A选项不合题意;
的值为时,,,不能判定是平行四边形,故B选项不合题意;
的值为时,,,不能判定是平行四边形,故C选项不合题意;
的值为时,,,能够判定是平行四边形,故D选项符合题意;
故选D.
本题考查平行四边形的判定,解题的关键是掌握平行四边形两组对角分别相等.
4.A
本题考查平行四边形的判定,根据平行四边形的判定方法一一判断即可.
解:A、对角线互相平分的四边形是平行四边形.正确.
B、对角线互相垂直的四边形不一定是平行四边形.错误.
C、对角线相等的四边形不一定是平行四边形.错误.
D、对角线互相垂直且相等的四边形不一定是平行四边形.错误.
故选:A.
5.D
根据平行四边形的判定定理分别进行分析即可.
解:A、不能判定四边形是平行四边形,故不符合题意;
B、不能判定四边形是平行四边形,故不符合题意;
C、不能判定四边形是平行四边形,故不符合题意;
D、根据对角线互相平分的四边形是平行四边形,能判定四边形是平行四边形,故符合题意
故选:D.
此题主要考查了平行四边形的判定,解题的关键是掌握平行四边形的判定定理.
6.D
选项A,B中的条件都只能证得,不能判定四边形是平行四边形.选项C中的条件,不能判定四边形是平行四边形.对于选项D提供两组对边分别平行,能判定四边形为平行四边形,本题考查了平行四边形的判定,正确掌握相关性质内容是解题的关键.
解:∵
∴
选项A不能判定四边形是平行四边形.
∵
∴
选项B不能判定四边形是平行四边形.
∵,
∴不能判定四边形ABCD是平行四边形.
选项C不能判定四边形是平行四边形.
∵,
∴.
又,
∴,
∴,
∴四边形是平行四边形
故选:D
7.B
本题考查了平行四边形的性质和判定,熟练掌握平行四边形的性质和判定是解题的关键.
证明四边形是平行四边形,根据平行四边形的性质即可得到结论.
解:∵,
∴四边形是平行四边形,
∵,
,
故选:B.
8.C
本题考查了平行四边形的判定与性质,熟练掌握知识点是解题的关键.
由四边形是平行四边形得到,,再证明四边形是平行四边形,则,即可求解周长.
解:∵四边形是平行四边形,
∴,,
∵,,
∴四边形是平行四边形,
∴,
∴周长为:,
故选:C.
9.3
图中的平行四边形有□ADFE,□BDEF,□CEDF,共三个,故答案为3.
10.
根据在四边形ABCD中,AB∥CD,AD∥BC,得出四边形ABCD是平行四边形,然后即可求解.
解:∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=7,
∴AO=AC=×7=.
故答案为:.
此题主要考查了平行四边形的判定与性质,得出四边形ABCD是平行四边形是解题关键.
11.(答案不唯一)
本题考查平行四边形的判定与性质,添加:,根据平行四边形的性质得,,继而得到,即可得证.掌握平行四边形的判定是解题的关键.
解:添加的一个条件为.理由如下:
∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形.
故答案为:(答案不唯一).
12.
本题考查了平行四边形的性质与判定,含度角的直角三角形的性质,由题意可得得,,cm,可证四边形是平行四边形,由直角三角形的性质可求的长,即可求解.
解:如图,过点A作于,过点作于,
由题意可得,,cm,
∴四边形是平行四边形,
∵,,
∴,
∴重叠四边形的面积(),
故答案为:.
13.2
本题主要考查平行四边形的判定和性质,由条件可证明四边形、为平行四边形,再利用面积的和差可证明,最后由等高四边形的条件即可得出答案.
解:∵,,
∴四边形、、、为平行四边形,
∴,
同理可得,,
∴,
即.
∵,,
∴;
故答案为:2.
14.(1)见解析
(2)添加(答案不唯一)
本题考查了平行四边形的性质与判定,全等三角形的判定;
(1)根据平行四边形的性质得出,,结合已知条件可得,即可证明;
(2)添加,依据一组对边平行且相等的四边形是平行四边形,即可求解.
(1)证明:∵四边形是平行四边形,
∴,,,
∵,
∴即,
在与中,
,
∴;
(2)添加(答案不唯一)
如图所示,连接.
∵四边形是平行四边形,
∴,即,
当时,四边形是平行四边形.
15.(1)见详解
(2)216
本题考查了平行四边的性质与判定,勾股定理,求平行四边的面积,正确掌握相关性质内容是解题的关键.
(1)先由平行线的性质得,因为得,则两组对应边互相平行的四边形是平行四边形,即可作答.
(2)运用勾股定理列式,,则,解出,再运算出,结合平行四边形的面积等于底乘高,即可作答.
(1)解:∵
∴
∵
∴
∴
∵
∴四边形是平行四边形;
(2)解:过点作
设
∵
∴在
在
则
解得
∴
则四边形的面积
16.(1)作图见解析
(2)平方单位
本题考查平移作图,三角形的面积和平行四边形的面积,
(1)分别将点、、向右平移个单位长度,得到点、、,然后顺次连接得到;
(2)根据扫过的面积等于平行四边形的面积三角形的面积解答即可;
解题的关键是掌握平移的性质,平行四边形的判定与性质.
(1)解:如图所示:即为所作;
(2)连接、,
∵将向右平移个单位长度后得到,点、的对应点分别为点、,
∴,,
∴四边形是平行四边形,
(平方单位),
∴扫过的面积为平方单位.
17.(1)见解析
(2)4
(1)根据平行四边形的性质得出,根据平行线的性质得出,根据角平分线的定义得出,根据等腰三角形的性质得出,根据余角的性质得出,根据等腰三角形的判定得出,即可证明结论;
(2)证明四边形为平行四边形,得出,求出,证明,,得出,,最后求出结果即可.
(1)证:∵平行四边形,
∴,
∴,
∵、分别平分和,
∴,
,
,
,
,
,
,
,
为的中点;
(2)解:根据解析(1)可知:,,
∴,
∴,
∵四边形为平行四边形,
∴,
∴四边形为平行四边形,
∴,
∴,
∵,
∴,,
∵,,
∴,,
∴,,
∴.
故答案为:4.
本题主要考查了平行四边形的判定和性质,等腰三角形的判定和性质,平行线的性质,角平分线定义,解题的关键是熟练掌握相关的判定和性质.
18.(1)证明见解析
(2)
本题考查了平行四边形的判定和性质,熟练掌握平行四边形的判定和性质是解题的关键;
(1)根据两组对边互相平行的四边形是平行四边形,即可得出结论;
(2)根据平行四边形的性质,平行四边形的对角相等即可解答.
(1)解:,,
四边形是平行四边形,
,;
(2)由(1)得四边形是平行四边形,
,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
