2025年中考二轮专题:“手拉手”模型与练习(含解析)
文档属性
| 名称 | 2025年中考二轮专题:“手拉手”模型与练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 526.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 17:00:05 | ||
图片预览




文档简介
专题七、“手拉手”模型
基础模型
图示 在 内且拉手线无交点 在 外且拉手线无交点 在 外且拉手线有交点
特点 在等腰 中,,在等腰 中,,,将 绕点 旋转一定角度后,连接 (称为"拉手线",左手拉左手,右手拉右手),相交于点 ,连接
结论 1. (即拉手线相等); 2. 平分 ; 3.
结论分析
结论 1:
证明:
在 和 中,
结论 2: 平分
证明: 如图,过点 分别作 于点 于点
∴ ,
∴ ,
∴ ,
∴ 平分 (角平分线的判定).
经典题目:
1.如图,AB=AD,AC=AE,DAB=CAE=50° ,以下四个结论:①△ADC≌△ABE;②CD=BE;③ DOB=50°;④点A在DOE的平分线上,其中结论正确的个数是( )
A.1 B.2 C.3 D.4
2.如图,,,三点在同一直线上,,都是等边三角形,连接,,:下列结论中正确的是( )
①△ACD≌△BCE;
②△CPQ是等边三角形;
③平分;
④△BPO≌△EDO.
A.①② B.①②③ C.①②④ D.①②③④
3.如图,和都是等腰直角三角形,,且点、、在同一条直线上,连接.
(1)的度数为 .
(2)若、分别是、的中点,连接,,,则的值为 .
4.如图,在正方形ABCD中,E是对角线BD上一点,将线段CE绕点C按顺时针方向旋转得到线段,连接,,.下列结论:①若,则;②;③若,则;④若,,则.其中正确的结论有 (填正确的序号)
5.在中,,点D是上一点(不与B,C重合),以为一边在 的右侧作,使,,连接 .
(1)如图1,若;
①说明:;
② 求 的度数.
(2)设,,如图2,则α,β之间有怎样的数量关系?请说明理由.
6.如图,在和中,,,若,连接、交于点P;
(1)求证∶.
(2)求的度数.
(3)如图(2),是等腰直角三角形,,,,点D是射线上的一点,连接,在直线上方作以点C为直角顶点的等腰直角,连接,若,求的值.
7.已知在和中,,,,点D是直线上的一动点(点D不与点B,C重合),连接.
(1)在图①中,当点D在边上时,求证:;(提示:证全等)
(2)在图②中,当点D在边的延长线上时,结论是否成立?若不成立,请猜想,,之间存在的数量关系,并说明理由;猜想与的位置关系,并说明理由;
(3)在图③中,当点D在边的反向延长线上时,补全图形,不需要写证明过程,直接写出,,间存在的数量关系.
8.(1)如图1,和都是等边三角形,且A、C、E在一条直线上.与相等吗?证明你的结论.
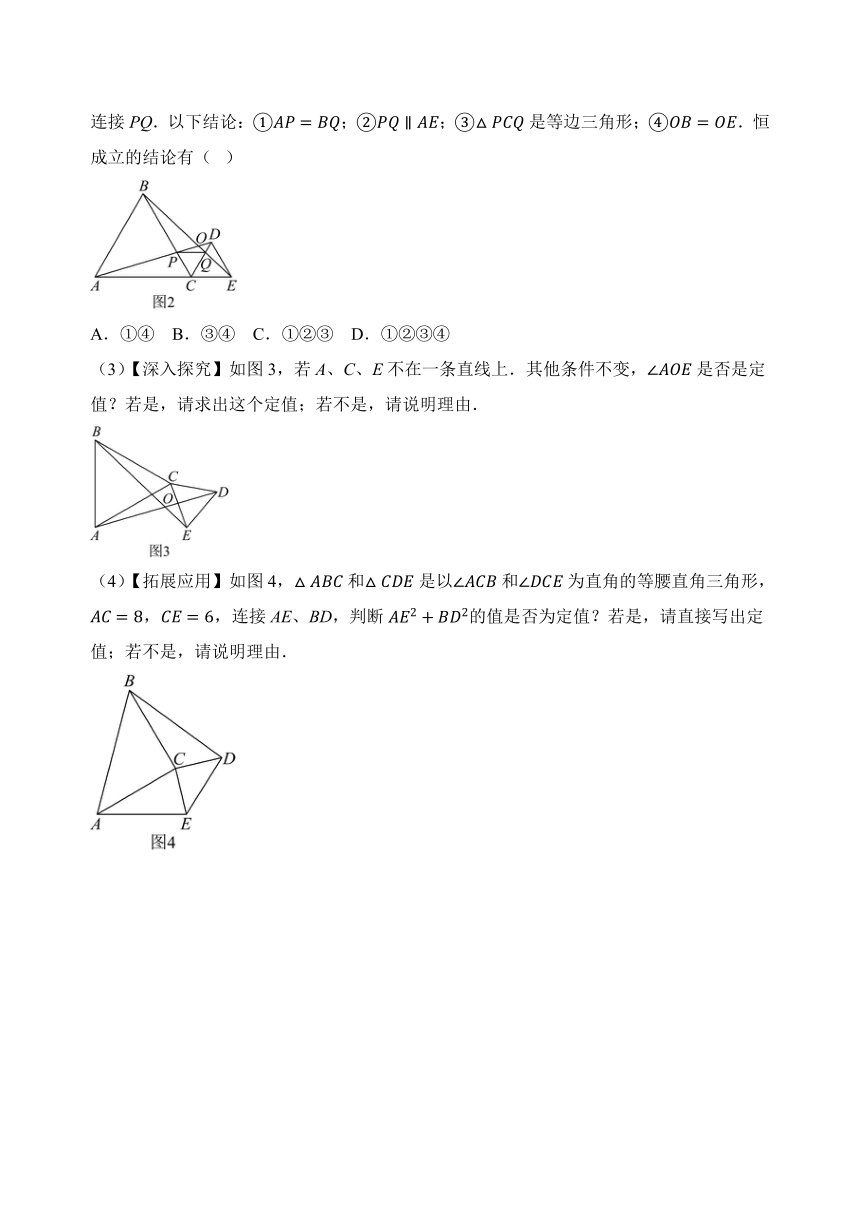
(2)【初步探究】如图2,若BE与AD交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下结论:①;②;③是等边三角形;④.恒成立的结论有( )
A.①④ B.③④ C.①②③ D.①②③④
(3)【深入探究】如图3,若A、C、E不在一条直线上.其他条件不变,是否是定值?若是,请求出这个定值;若不是,请说明理由.
(4)【拓展应用】如图4,和是以和为直角的等腰直角三角形,,,连接AE、BD,判断的值是否为定值?若是,请直接写出定值;若不是,请说明理由.
9.【探究发现】(1)如图1,在四边形中,对角线,垂足是O,求证:.
【拓展迁移】(2)如图2.以三角形的边、为边向外作正方形和正方形,求证:.
(3)如图3,在(2)小题条件不变的情况下,连接,若,,,则的长_____________.(直接填写答案)
10.【理解概念】当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中有一个三角形是等腰直角三角形,则把这条对角线叫做这个四边形的“等腰直角线”,把这个四边形叫做“等腰直角四边形”,
当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中一个三角形是等腰直角三角形,另一个三角形是等腰三角形,则把这条对角线叫做这个四边形的“真等腰直角线”,把这个四边形叫做“真等腰直角四边形”.
(1)【巩固新知】如图①,若AD=3,AD=DB=DC,BC=3,则四边形ABCD______(填“是”或“否”)真等腰直角四边形.
(2)【深度理解】在图①中,如果四边形ABCD是真等腰直角四边形,且∠BDC=90°,对角线BD是这个四边形的真等腰直角线,当AD=4,AB=3时,则边BC的长是______.
(3)如图②,四边形ABCD与四边形ABDE都是等腰直角四边形,且∠BDC=90°,∠ADE=90°,BD>AD>AB,对角线BD、AD分别是这两个四边形的等腰直角线.求证:AC=BE.
(4)【拓展提高】在图3中,已知:四边形ABCD是等腰直角四边形,对角线BD是这个四边形的等腰直角线.若BD正好是分得的等腰直角三角形的一条直角边,且AD=3,AB=4,∠BAD=45°,求AC的长.
参考答案
1.D
【分析】根据全等三角形的判定及角平分线的性质即可依次判断.
【详解】∵DAB=CAE
∴DAB+BAC=CAE+BAC
∴DAC=EAB
∵AB=AD,AC=AE
∴△ADC≌△ABE
∴CD=BE,故①②正确;
∵△ADC≌△ABE
∴ADC =ABE
设AB与CD交于G点,
∵AGD =BGC
∴DOB=DAB=50°,故③正确;
过点A作AF⊥CD于F点,过点A作AH⊥BE于H点,
则AF、AH分别是△ADC与△ABE边上的高
∵△ADC≌△ABE
∴AF=AH
∴点A在DOE的平分线上,④正确
故选D.
【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知角平分线的性质与判定.
2.B
【分析】利用等边三角形的性质,三角形的全等,逐一判断即可.
【详解】∵△ABC,△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠PCQ =∠ECD+∠PCQ,∠PCD=60°,
∴∠ACD =∠BCE,
∴△ACD≌△BCE,
∴①的说法是正确的;
∵△ACD≌△BCE,
∴∠PDC =∠QEC,
∵∠PCD=∠QCE=60°,CD=CE,
∴△PCD≌△QCE,
∴PC=QC,
∴△CPQ是等边三角形;
∴②的说法是正确的;
∵△PCD≌△QCE,
∴PD=QE,,
过点C作CG⊥PD,垂足为G,CH⊥QE,垂足为H,
∴,
∴CG=CH,
∴平分,
∴③的说法是正确的;
无法证明△BPO≌△EDO.
∴④的说法是错误的;
故答案为①②③,
故选B.
【点睛】本题考查了等边三角形的性质与判定,三角形的全等与性质,角平分线的性质定理,熟练掌握等边三角形的性质,灵活进行三角形全等的判定,活用角的平分线性质定理的逆定理是解题的关键.
3. 90°
【分析】(1)先根据已知条件证明△AOC ≌△BOD,再根据等腰直角三角形的性质计算即可.
(2)先利用中位线定理得出BD的长,再根据全等三角形的性质得出AC,利用勾股定理得出AP,根据△AOC≌△BOD,利用相似比和面积的关系计算即可.
【详解】(1)∵△AOB与△COD都是等腰直角三角形
∴ OA=OB. OC=OD
∠ODC= ∠OCD=45°
又∵ ∠AOB-∠BOC= ∠COD- ∠BOC
∴ ∠AOC=∠BOD,
即OA=OB,OC=OD,
∠AOC= ∠BOD
∴ △AOC ≌△BOD (SAS) ,
∴ ∠BDO=∠ACO=180°-∠OCD=135°,
∴ ∠ADB=∠BDO-∠ODC=135°-45°=90°;
(2)由题意可知PC是△ABD的中位线,
∴ BD=2PC=2, PC∥BD
∴ △ACP是直角三角形,
又∵△AOC≌△BOD
∴AC=CD=BD=2,
∴AP=
AB=
又△COD∽△AOB,
∴;
故答案为:90°;
【点睛】本题考查手拉手模型、相似三角形、全等三角形、勾股定理、相似三角形的性质.了解手拉手模型对解决本题有很大的作用.熟悉相似三角形的性质、判定是关键.
4.①②④
【分析】证明△≌△,可得,,,根据三角形内角和定理可判断①正确;在Rt△中,,即,从而判断②正确;③证明,故可判断③错误;连接AC与BD交于点O,计算可得CO=9,根据正弦定理可判断④正确.
【详解】解:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵线段CE绕点C按顺时针方向旋转得到线段,
∴,,
∴△是等腰直角三角形,
∴,
∴,
即,
在△和△中,
∴△≌△(SAS),
∴,,
∴,
即△是直角三角形,
∵四边形ABCD是正方形,E在对角线BD上,
∴,
∴,,
∴,
∵,
∴,故①正确;
在Rt△中,,
在Rt△中,,
∴,故②正确;
若,则,
在Rt△中,,
∵,
,故③错误;
连接AC与BD交于点O,如图,
∵四边形ABCD是正方形,
∴∠EOC=90°,且是等腰直角三角形,
∵
∴ CO=,
∵,
∴sin∠DEC=,故④正确.
故答案为:①②④.
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,旋转的性质,解直角三角形等知识,解本题的关键是学会添加常用的辅助线,构造直角三角形解决问题.
5.(1)①见解析
②
(2).理由见解析
【分析】本题考查全等三角形的判定与性质,三角形内角和定理,熟练掌握全等三角形的判定与性质是解题的关键.
(1)①利用定理证明即可;
②利用全等三角形的性质得出,再利用三角形内角和定理求解即可;
(2)利用定理证明,得到,从而得到,再根据三角形内角和定理求解即可.
【详解】(1)①证明:因为,
所以,即.
在 和中,,
所以.
②解: 由 ①,可得.
所以.
所以.
(2)解:.
理由:因为,
所以,即.
在 和中, ,
所以,
所以.
所以,
所以.
因为,
所以.
6.(1)见解析
(2)
(3)或
【分析】本题考查了全等三角形的性质与判定,等边三角形的性质,三角形内角和定理的应用;
(1)根据题意得出,即可证明;
(2)根据题意可得是等边三角形,根据(1)的结论可得,进而根据三角形的内角和定理,即可求解;
(3)分情况讨论,当在线段上时,当在的延长线上时,证明,得出,结合图形,即可求解.
【详解】(1)证明:∵,
∴,
又∵,,
∴;
(2)解:∵,,
∴是等边三角形,
∴,
∵,
∴,
∴
;
(3)解:如图所示,当在线段上时,
∵是以点为直角顶点的等腰直角三角形,
∴,
又∵,,
∴,
∴,
∴,
∵,
∴,
如图所示,当在的延长线上时,
同理可得,∴,
∴,
∵,
∴,
综上所述,或.
7.(1)见解析
(2)不成立,存在的数量关系为,位置关系为,理由见解析
(3)图见解析,
【分析】本题考查了等腰直角三角形的性质,全等三角形的判定与性质.
(1)求出,证明,根据全等三角形的性质可得结论;
(2)求出,证明,根据全等三角形的性质可得,,即可得,然后由是等腰直角三角形可得,,进而求出即可得出结论;
(3)如图3,求出,证明,根据全等三角形的性质可得出结论.
【详解】(1)证明:∵,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:不成立,存在的数量关系为,位置关系为,理由如下:
∵,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴;
(3)解:存在的数量关系为,理由如下:
如图3,
∵,
∴,
又∵,,
∴,
∴,
∴.
8.(1),见解析
(2)C
(3)是,
(4)是,
【分析】(1)证明,即可得出结论;
(2)证明,得,可判定①成立,,又,可得是等边三角形,可判定③成立;,则,可得,可判定②成立;由于点O不一定是的中点,可判定④不是恒成立;
(3)设交于M,由(1)知:,又,,则∴,即可求得.
(4)连接交于N,连接交于M,交,由等腰直角 三我性质与勾股定理求得,,再证明,得,从而求得 ,由勾股定理得,,,,即可由求解.
【详解】解:(1),
证明:和均为等边三角形,
,,.
∴
.
在和中,
,
.
.
(2)和均为等边三角形,
∴.
∴,
∴,
由(1)知:
∴
又∵
∴
∴,故①成立;
∵
∴
∵
∴是等边三角形,故③成立;
∴
∴
∴,故②成立;
由于点O不一定是的中点,故④不是恒成立;
故选:C.
(3)设交于M,如图3,
由(1)知:
∵,,
∴
∴.
(4)是,。
理由:连接交于N,连接交于M,交,如图4,
∵和是以和为直角的等腰直角三角形,
∴,,,
∴,,
∴,即,
∴,
∴,
∵,
又∵,
∴,
∴,,
∵,
∴,,
∴.
∴,是定值.
【点睛】本题考查等腰三角形的性质,等边三角形的判定与性质,等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,三角形内角和与外角的性质,熟练掌握“手拉手”模型是解题的关键.
9.(1)见解析;(2)见解析;(3).
【分析】(1)根据,利用勾股定理分别求出和即可证明结论;
(2)利用正方形的性质证明△CAE≌△GAB(SAS),可得∠CEA=∠GBA,根据∠GBA+∠ANB=90°等量代换求出∠EMN=90°即可;
(3)利用勾股定理分别求出AE、CG和BE,然后利用(1)中结论求出BC即可.
【详解】解:(1)∵,
∴∠AOD=∠AOB=∠COD=∠BOC=90°,
由勾股定理得:,,
∴;
(2)∵在正方形和正方形中,AC=AG,AE=AB,∠CAG=∠EAB=90°,
∴∠CAG+∠GAE=∠EAB+∠GAE,即∠CAE=∠GAB,
∴△CAE≌△GAB(SAS),
∴∠CEA=∠GBA,
∵∠GBA+∠ANB=90°,∠ANB=∠MNE,
∴∠CEA+∠MNE=90°,
∴∠EMN=90°,
∴;
(3)如图3,连接CG,BE,
∵,,,
∴AC=8,AE=,
∴AB=10,
∴CG=,BE=,
∵,
∴由(1)可知:,即,
∵BC>0,
∴.
故答案为:.
【点睛】本题主要考查了勾股定理,全等三角形的判定和性质,熟练掌握勾股定理是解答此题的关键.
10.(1)是
(2)4或3
(3)见解析
(4)AC=或.
【分析】(1)利用勾股定理的逆定理证明∠BDC=90°,从而△BDC是等腰直角三角形,又因为△ABD是等腰三角形,即可得出结论;
(2)由题意知△ABD是等腰三角形,当AD=BD=4时,由勾股定理得:BC=4,当BD=AB=3时,由勾股定理得:BC=3;
(3)利用SAS证明△ADC≌△EDB,得AC=BE;
(4)分∠BDC=90°和∠DBC=90°,分别构造等腰直角三角形,利用(3)中全等进行转化,从而解决问题.
【详解】(1)解:∵AD=3,AD=DB=DC,
∴BD=CD=3,
∵BD2+CD2=18,BC2=(3)2=18,
∴BD2+CD2=BC2,
∴△BDC是等腰直角三角形,
∵△ABD是等腰三角形,
∴四边形ABCD是真等腰直角四边形,
故答案为:是;
(2)解:∵对角线BD是这个四边形的真等腰直角线,
∴△ABD是等腰三角形,
当AD=BD=4时,由勾股定理得:BC==4,
当BD=AB=3时,由勾股定理得:BC==3,
综上:BC=4或3,
故答案为:4或3;
(3)解:由题意知:△BDC和△ADE都是等腰直角三角形,
∴BD=CD,AD=DE,∠BDC=∠ADE=90°,
∴∠ADC=∠EDB,
∴△ADC≌△EDB(SAS),
∴AC=BE;
(4)解:由题意知:△BDC是等腰直角三角形,
当∠BDC=90°时,如图,作DE⊥AD,取DE=AD,连接AE,BE,
由(3)同理得△ADC≌△EDB(SAS),
∴AC=BE,
∵AD=3,△ADE是等腰直角三角形,
∴AE=3,∠EAD=45°,
∵∠DAB=45°,
∴∠EAB=90°,
由勾股定理得BE=,
∴AC=;
当∠DBC=90°时,如图,同理可得
AE=4,
DE=AC=,
综上:AC=或.
【点睛】本题主要考查了等腰直角三角形和等腰三角形的性质,全等三角形的判定与性质,勾股定理的应用,读懂题意,作辅助线构造全等三角形是解题的关键,注意问题设置的层次性.
基础模型
图示 在 内且拉手线无交点 在 外且拉手线无交点 在 外且拉手线有交点
特点 在等腰 中,,在等腰 中,,,将 绕点 旋转一定角度后,连接 (称为"拉手线",左手拉左手,右手拉右手),相交于点 ,连接
结论 1. (即拉手线相等); 2. 平分 ; 3.
结论分析
结论 1:
证明:
在 和 中,
结论 2: 平分
证明: 如图,过点 分别作 于点 于点
∴ ,
∴ ,
∴ ,
∴ 平分 (角平分线的判定).
经典题目:
1.如图,AB=AD,AC=AE,DAB=CAE=50° ,以下四个结论:①△ADC≌△ABE;②CD=BE;③ DOB=50°;④点A在DOE的平分线上,其中结论正确的个数是( )
A.1 B.2 C.3 D.4
2.如图,,,三点在同一直线上,,都是等边三角形,连接,,:下列结论中正确的是( )
①△ACD≌△BCE;
②△CPQ是等边三角形;
③平分;
④△BPO≌△EDO.
A.①② B.①②③ C.①②④ D.①②③④
3.如图,和都是等腰直角三角形,,且点、、在同一条直线上,连接.
(1)的度数为 .
(2)若、分别是、的中点,连接,,,则的值为 .
4.如图,在正方形ABCD中,E是对角线BD上一点,将线段CE绕点C按顺时针方向旋转得到线段,连接,,.下列结论:①若,则;②;③若,则;④若,,则.其中正确的结论有 (填正确的序号)
5.在中,,点D是上一点(不与B,C重合),以为一边在 的右侧作,使,,连接 .
(1)如图1,若;
①说明:;
② 求 的度数.
(2)设,,如图2,则α,β之间有怎样的数量关系?请说明理由.
6.如图,在和中,,,若,连接、交于点P;
(1)求证∶.
(2)求的度数.
(3)如图(2),是等腰直角三角形,,,,点D是射线上的一点,连接,在直线上方作以点C为直角顶点的等腰直角,连接,若,求的值.
7.已知在和中,,,,点D是直线上的一动点(点D不与点B,C重合),连接.
(1)在图①中,当点D在边上时,求证:;(提示:证全等)
(2)在图②中,当点D在边的延长线上时,结论是否成立?若不成立,请猜想,,之间存在的数量关系,并说明理由;猜想与的位置关系,并说明理由;
(3)在图③中,当点D在边的反向延长线上时,补全图形,不需要写证明过程,直接写出,,间存在的数量关系.
8.(1)如图1,和都是等边三角形,且A、C、E在一条直线上.与相等吗?证明你的结论.
(2)【初步探究】如图2,若BE与AD交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下结论:①;②;③是等边三角形;④.恒成立的结论有( )
A.①④ B.③④ C.①②③ D.①②③④
(3)【深入探究】如图3,若A、C、E不在一条直线上.其他条件不变,是否是定值?若是,请求出这个定值;若不是,请说明理由.
(4)【拓展应用】如图4,和是以和为直角的等腰直角三角形,,,连接AE、BD,判断的值是否为定值?若是,请直接写出定值;若不是,请说明理由.
9.【探究发现】(1)如图1,在四边形中,对角线,垂足是O,求证:.
【拓展迁移】(2)如图2.以三角形的边、为边向外作正方形和正方形,求证:.
(3)如图3,在(2)小题条件不变的情况下,连接,若,,,则的长_____________.(直接填写答案)
10.【理解概念】当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中有一个三角形是等腰直角三角形,则把这条对角线叫做这个四边形的“等腰直角线”,把这个四边形叫做“等腰直角四边形”,
当一个凸四边形的一条对角线把原四边形分成两个三角形.若其中一个三角形是等腰直角三角形,另一个三角形是等腰三角形,则把这条对角线叫做这个四边形的“真等腰直角线”,把这个四边形叫做“真等腰直角四边形”.
(1)【巩固新知】如图①,若AD=3,AD=DB=DC,BC=3,则四边形ABCD______(填“是”或“否”)真等腰直角四边形.
(2)【深度理解】在图①中,如果四边形ABCD是真等腰直角四边形,且∠BDC=90°,对角线BD是这个四边形的真等腰直角线,当AD=4,AB=3时,则边BC的长是______.
(3)如图②,四边形ABCD与四边形ABDE都是等腰直角四边形,且∠BDC=90°,∠ADE=90°,BD>AD>AB,对角线BD、AD分别是这两个四边形的等腰直角线.求证:AC=BE.
(4)【拓展提高】在图3中,已知:四边形ABCD是等腰直角四边形,对角线BD是这个四边形的等腰直角线.若BD正好是分得的等腰直角三角形的一条直角边,且AD=3,AB=4,∠BAD=45°,求AC的长.
参考答案
1.D
【分析】根据全等三角形的判定及角平分线的性质即可依次判断.
【详解】∵DAB=CAE
∴DAB+BAC=CAE+BAC
∴DAC=EAB
∵AB=AD,AC=AE
∴△ADC≌△ABE
∴CD=BE,故①②正确;
∵△ADC≌△ABE
∴ADC =ABE
设AB与CD交于G点,
∵AGD =BGC
∴DOB=DAB=50°,故③正确;
过点A作AF⊥CD于F点,过点A作AH⊥BE于H点,
则AF、AH分别是△ADC与△ABE边上的高
∵△ADC≌△ABE
∴AF=AH
∴点A在DOE的平分线上,④正确
故选D.
【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知角平分线的性质与判定.
2.B
【分析】利用等边三角形的性质,三角形的全等,逐一判断即可.
【详解】∵△ABC,△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠PCQ =∠ECD+∠PCQ,∠PCD=60°,
∴∠ACD =∠BCE,
∴△ACD≌△BCE,
∴①的说法是正确的;
∵△ACD≌△BCE,
∴∠PDC =∠QEC,
∵∠PCD=∠QCE=60°,CD=CE,
∴△PCD≌△QCE,
∴PC=QC,
∴△CPQ是等边三角形;
∴②的说法是正确的;
∵△PCD≌△QCE,
∴PD=QE,,
过点C作CG⊥PD,垂足为G,CH⊥QE,垂足为H,
∴,
∴CG=CH,
∴平分,
∴③的说法是正确的;
无法证明△BPO≌△EDO.
∴④的说法是错误的;
故答案为①②③,
故选B.
【点睛】本题考查了等边三角形的性质与判定,三角形的全等与性质,角平分线的性质定理,熟练掌握等边三角形的性质,灵活进行三角形全等的判定,活用角的平分线性质定理的逆定理是解题的关键.
3. 90°
【分析】(1)先根据已知条件证明△AOC ≌△BOD,再根据等腰直角三角形的性质计算即可.
(2)先利用中位线定理得出BD的长,再根据全等三角形的性质得出AC,利用勾股定理得出AP,根据△AOC≌△BOD,利用相似比和面积的关系计算即可.
【详解】(1)∵△AOB与△COD都是等腰直角三角形
∴ OA=OB. OC=OD
∠ODC= ∠OCD=45°
又∵ ∠AOB-∠BOC= ∠COD- ∠BOC
∴ ∠AOC=∠BOD,
即OA=OB,OC=OD,
∠AOC= ∠BOD
∴ △AOC ≌△BOD (SAS) ,
∴ ∠BDO=∠ACO=180°-∠OCD=135°,
∴ ∠ADB=∠BDO-∠ODC=135°-45°=90°;
(2)由题意可知PC是△ABD的中位线,
∴ BD=2PC=2, PC∥BD
∴ △ACP是直角三角形,
又∵△AOC≌△BOD
∴AC=CD=BD=2,
∴AP=
AB=
又△COD∽△AOB,
∴;
故答案为:90°;
【点睛】本题考查手拉手模型、相似三角形、全等三角形、勾股定理、相似三角形的性质.了解手拉手模型对解决本题有很大的作用.熟悉相似三角形的性质、判定是关键.
4.①②④
【分析】证明△≌△,可得,,,根据三角形内角和定理可判断①正确;在Rt△中,,即,从而判断②正确;③证明,故可判断③错误;连接AC与BD交于点O,计算可得CO=9,根据正弦定理可判断④正确.
【详解】解:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵线段CE绕点C按顺时针方向旋转得到线段,
∴,,
∴△是等腰直角三角形,
∴,
∴,
即,
在△和△中,
∴△≌△(SAS),
∴,,
∴,
即△是直角三角形,
∵四边形ABCD是正方形,E在对角线BD上,
∴,
∴,,
∴,
∵,
∴,故①正确;
在Rt△中,,
在Rt△中,,
∴,故②正确;
若,则,
在Rt△中,,
∵,
,故③错误;
连接AC与BD交于点O,如图,
∵四边形ABCD是正方形,
∴∠EOC=90°,且是等腰直角三角形,
∵
∴ CO=,
∵,
∴sin∠DEC=,故④正确.
故答案为:①②④.
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,旋转的性质,解直角三角形等知识,解本题的关键是学会添加常用的辅助线,构造直角三角形解决问题.
5.(1)①见解析
②
(2).理由见解析
【分析】本题考查全等三角形的判定与性质,三角形内角和定理,熟练掌握全等三角形的判定与性质是解题的关键.
(1)①利用定理证明即可;
②利用全等三角形的性质得出,再利用三角形内角和定理求解即可;
(2)利用定理证明,得到,从而得到,再根据三角形内角和定理求解即可.
【详解】(1)①证明:因为,
所以,即.
在 和中,,
所以.
②解: 由 ①,可得.
所以.
所以.
(2)解:.
理由:因为,
所以,即.
在 和中, ,
所以,
所以.
所以,
所以.
因为,
所以.
6.(1)见解析
(2)
(3)或
【分析】本题考查了全等三角形的性质与判定,等边三角形的性质,三角形内角和定理的应用;
(1)根据题意得出,即可证明;
(2)根据题意可得是等边三角形,根据(1)的结论可得,进而根据三角形的内角和定理,即可求解;
(3)分情况讨论,当在线段上时,当在的延长线上时,证明,得出,结合图形,即可求解.
【详解】(1)证明:∵,
∴,
又∵,,
∴;
(2)解:∵,,
∴是等边三角形,
∴,
∵,
∴,
∴
;
(3)解:如图所示,当在线段上时,
∵是以点为直角顶点的等腰直角三角形,
∴,
又∵,,
∴,
∴,
∴,
∵,
∴,
如图所示,当在的延长线上时,
同理可得,∴,
∴,
∵,
∴,
综上所述,或.
7.(1)见解析
(2)不成立,存在的数量关系为,位置关系为,理由见解析
(3)图见解析,
【分析】本题考查了等腰直角三角形的性质,全等三角形的判定与性质.
(1)求出,证明,根据全等三角形的性质可得结论;
(2)求出,证明,根据全等三角形的性质可得,,即可得,然后由是等腰直角三角形可得,,进而求出即可得出结论;
(3)如图3,求出,证明,根据全等三角形的性质可得出结论.
【详解】(1)证明:∵,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:不成立,存在的数量关系为,位置关系为,理由如下:
∵,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴;
(3)解:存在的数量关系为,理由如下:
如图3,
∵,
∴,
又∵,,
∴,
∴,
∴.
8.(1),见解析
(2)C
(3)是,
(4)是,
【分析】(1)证明,即可得出结论;
(2)证明,得,可判定①成立,,又,可得是等边三角形,可判定③成立;,则,可得,可判定②成立;由于点O不一定是的中点,可判定④不是恒成立;
(3)设交于M,由(1)知:,又,,则∴,即可求得.
(4)连接交于N,连接交于M,交,由等腰直角 三我性质与勾股定理求得,,再证明,得,从而求得 ,由勾股定理得,,,,即可由求解.
【详解】解:(1),
证明:和均为等边三角形,
,,.
∴
.
在和中,
,
.
.
(2)和均为等边三角形,
∴.
∴,
∴,
由(1)知:
∴
又∵
∴
∴,故①成立;
∵
∴
∵
∴是等边三角形,故③成立;
∴
∴
∴,故②成立;
由于点O不一定是的中点,故④不是恒成立;
故选:C.
(3)设交于M,如图3,
由(1)知:
∵,,
∴
∴.
(4)是,。
理由:连接交于N,连接交于M,交,如图4,
∵和是以和为直角的等腰直角三角形,
∴,,,
∴,,
∴,即,
∴,
∴,
∵,
又∵,
∴,
∴,,
∵,
∴,,
∴.
∴,是定值.
【点睛】本题考查等腰三角形的性质,等边三角形的判定与性质,等腰直角三角形的性质,全等三角形的判定与性质,勾股定理,三角形内角和与外角的性质,熟练掌握“手拉手”模型是解题的关键.
9.(1)见解析;(2)见解析;(3).
【分析】(1)根据,利用勾股定理分别求出和即可证明结论;
(2)利用正方形的性质证明△CAE≌△GAB(SAS),可得∠CEA=∠GBA,根据∠GBA+∠ANB=90°等量代换求出∠EMN=90°即可;
(3)利用勾股定理分别求出AE、CG和BE,然后利用(1)中结论求出BC即可.
【详解】解:(1)∵,
∴∠AOD=∠AOB=∠COD=∠BOC=90°,
由勾股定理得:,,
∴;
(2)∵在正方形和正方形中,AC=AG,AE=AB,∠CAG=∠EAB=90°,
∴∠CAG+∠GAE=∠EAB+∠GAE,即∠CAE=∠GAB,
∴△CAE≌△GAB(SAS),
∴∠CEA=∠GBA,
∵∠GBA+∠ANB=90°,∠ANB=∠MNE,
∴∠CEA+∠MNE=90°,
∴∠EMN=90°,
∴;
(3)如图3,连接CG,BE,
∵,,,
∴AC=8,AE=,
∴AB=10,
∴CG=,BE=,
∵,
∴由(1)可知:,即,
∵BC>0,
∴.
故答案为:.
【点睛】本题主要考查了勾股定理,全等三角形的判定和性质,熟练掌握勾股定理是解答此题的关键.
10.(1)是
(2)4或3
(3)见解析
(4)AC=或.
【分析】(1)利用勾股定理的逆定理证明∠BDC=90°,从而△BDC是等腰直角三角形,又因为△ABD是等腰三角形,即可得出结论;
(2)由题意知△ABD是等腰三角形,当AD=BD=4时,由勾股定理得:BC=4,当BD=AB=3时,由勾股定理得:BC=3;
(3)利用SAS证明△ADC≌△EDB,得AC=BE;
(4)分∠BDC=90°和∠DBC=90°,分别构造等腰直角三角形,利用(3)中全等进行转化,从而解决问题.
【详解】(1)解:∵AD=3,AD=DB=DC,
∴BD=CD=3,
∵BD2+CD2=18,BC2=(3)2=18,
∴BD2+CD2=BC2,
∴△BDC是等腰直角三角形,
∵△ABD是等腰三角形,
∴四边形ABCD是真等腰直角四边形,
故答案为:是;
(2)解:∵对角线BD是这个四边形的真等腰直角线,
∴△ABD是等腰三角形,
当AD=BD=4时,由勾股定理得:BC==4,
当BD=AB=3时,由勾股定理得:BC==3,
综上:BC=4或3,
故答案为:4或3;
(3)解:由题意知:△BDC和△ADE都是等腰直角三角形,
∴BD=CD,AD=DE,∠BDC=∠ADE=90°,
∴∠ADC=∠EDB,
∴△ADC≌△EDB(SAS),
∴AC=BE;
(4)解:由题意知:△BDC是等腰直角三角形,
当∠BDC=90°时,如图,作DE⊥AD,取DE=AD,连接AE,BE,
由(3)同理得△ADC≌△EDB(SAS),
∴AC=BE,
∵AD=3,△ADE是等腰直角三角形,
∴AE=3,∠EAD=45°,
∵∠DAB=45°,
∴∠EAB=90°,
由勾股定理得BE=,
∴AC=;
当∠DBC=90°时,如图,同理可得
AE=4,
DE=AC=,
综上:AC=或.
【点睛】本题主要考查了等腰直角三角形和等腰三角形的性质,全等三角形的判定与性质,勾股定理的应用,读懂题意,作辅助线构造全等三角形是解题的关键,注意问题设置的层次性.
同课章节目录
