2025年中考二轮专题:“梅涅劳斯”模型与练习(含解析)
文档属性
| 名称 | 2025年中考二轮专题:“梅涅劳斯”模型与练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 608.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览




文档简介
专题八、“梅涅劳斯”模型
模型证明
1)梅涅劳斯定理模型
如图1,如果一条直线与 的三边 或其延长线交于 点,那么
其中:这条直线叫 的梅氏线, 叫梅氏三角形。
证明:
如图2,过点 作 ,交 的延长线于点 ,易证:
2)梅涅劳斯定理的逆定理模型
如图1,若 分别是 的三边 或其延长线的三点,如果
则 三点共线。
证明:假设 三点不共线,直线 与 交于 ,由梅涅劳斯定理得
即 与 重合, 三点共线。
经典题目:
1.请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设,,依次是的三边,,或其延长线上的点,且这三点共线,则满足.
这个定理的证明步骤如下:
情况①:如图1,直线交的边于点,交边于点,交边的延长线与点.
过点作交于点,则,(依据),
∴,
∴,即.
情况②:如图2,直线分别交的边,,的延长线于点,,.…
(1)情况①中的依据指: ;
(2)请你根据情况①的证明思路完成情况②的证明;
(3)如图3,,分别是的边,上的点,且,连接并延长,交的延长线于点,那么
2.请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设D,E,F依次是的三边及其延长线上的点,且这三点共线,则满足.这个定理的证明步骤如下:
情况①:如图1,直线交的边于点D,交边于点E,交边的延长线于点F.过点C作交于点G,
则,(依据)
∴.
∴,
即.
情况②:如图2,直线分别交的边的延长线于点D,E,F…
(1)情况①中的依据指:_______.
(2)请你根据情况①的证明思路完成情况②的证明.
(3)如图3,D、E分别是的边上的点,且,连接并延长,交的延长线于点F,那么______.
3.请阅读下列材料,完成任务.
梅涅劳斯(Menelaus)是公元1世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交(交点不能是三角形的顶点),可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积.该定理被称为梅涅劳斯定理,简称梅氏定理.
如图1,直线交线段于点,交线段于点,交延长线于点D,可截得六条线段,则这六条线段满足,下面是该定理的一部分证明过程:
证明:如图2,过点作,交延长线于点,则有(依据),…
(1)上述过程中的“依据”指的是 ;
(2)请将该定理的证明过程补充完整.
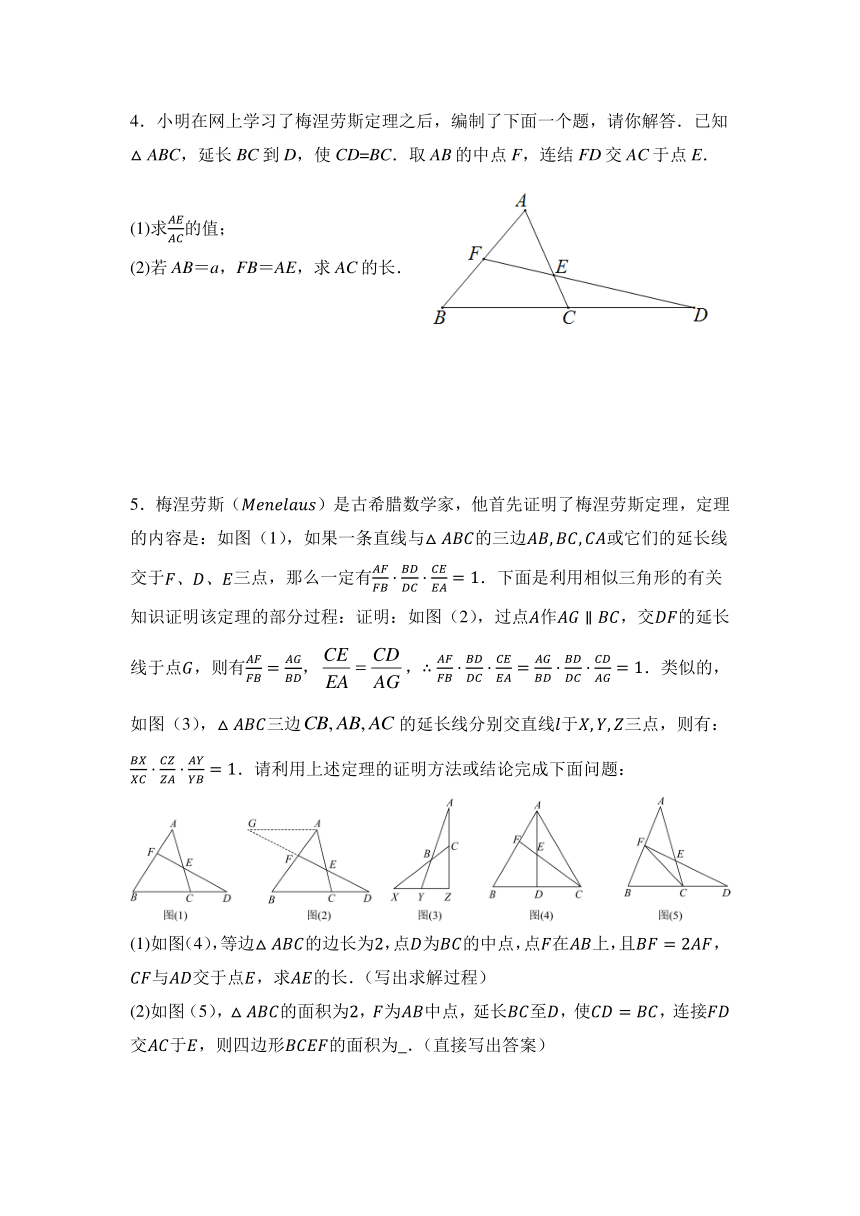
4.小明在网上学习了梅涅劳斯定理之后,编制了下面一个题,请你解答.已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
(1)求的值;
(2)若AB=a,FB=AE,求AC的长.
5.梅涅劳斯()是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与的三边或它们的延长线交于三点,那么一定有.下面是利用相似三角形的有关知识证明该定理的部分过程:证明:如图(2),过点作,交的延长线于点,则有,,.类似的,如图(3),三边的延长线分别交直线于三点,则有:.请利用上述定理的证明方法或结论完成下面问题:
(1)如图(4),等边的边长为,点为的中点,点在上,且,与交于点,求的长.(写出求解过程)
(2)如图(5),的面积为,为中点,延长至,使,连接交于,则四边形的面积为 .(直接写出答案)
6.梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作,交DF的延长线于点G,
则有,,
∴.
请用上述定理的证明方法解决以下问题:
(1)如图(3),△ABC三边CB,AB,AC的延长线分别交直线l于X,Y,Z三点,证明:.
(2)如图(4),等边△ABC的边长为2,点D为BC的中点,点F在AB上,且,CF与AD交于点E,则AE的长为________.
(3)如图(5),△ABC的面积为2,F为AB中点,延长BC至D,使,连接FD交AC于E,则四边形BCEF的面积为________.
7.梅涅劳斯定理
梅涅劳斯()是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作,交DF的延长线于点G,则有.
任务:(1)请你将上述材料中的剩余的证明过程补充完整;
(2)如图(3),在中,,,点D为BC的中点,点F在AB上,且,CF与AD交于点E,则________.
8.请阅读下列材料,并完成相应的任务.
梅涅劳斯()是公元1世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交(交点不能是三角形的顶点),可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积.该定理被称为梅涅劳斯定理,简称梅氏定理.
如图1,直线交线段于点,交线段于点,交延长线于点,可截得六条线段、、、、、,则这六条线段满足.
下面是该定理的一部分证明过程:
证明:如图2,过点作,交延长线于点
则有(依据),…
(1)上述过程中的依据指的是________;
(2)请将该定理的证明过程补充完整.
(3)在图1中,若点是的中点,,则的值为________;
(4)在图1中,若,,则的值为________.
9.梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图1,如果一条直线与的三边或它们的延长线交于三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图2,过点作,交的延长线于点,则有,,
∴,
.
请用上述定理的证明方法解决以下问题:
(1)如图3,三边的延长线分别交直线于三点,证明:.
请用上述定理的证明方法或结论解决以下问题:
(2)如图4,等边的边长为3,点为的中点,点在上,且与交于点,试求的长.
(3)如图5,的面积为4,F为中点,延长至,使,连接交于,求四边形的面积.
10.如图,三边,,的延长线分别交直线于,,三点,证明:.(即证明梅涅劳斯定理的其中一种形式)
参考答案
1.(1)两条直线被一组平行线所截,所得的对应线段成比例
(2)证明过程见详解
(3)
【分析】(1)根据平行线分线段成比例定理解决问题即可;
(2)如图2中,作交于,模仿情况①的方法解决问题即可;
(3)利用梅氏定理即可解决问题.
【详解】(1)解:情况①中的依据是:两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:两条直线被一组平行线所截,所得的对应线段成比例.
(2)证明:如图2中,作交于,
则有,
∴,
∴,则,变形得,
∴,
∵,
∴,
∴,
∴,
∴.
(3)解:∵,,
∴,
∴.
故答案为:.
【点睛】本题考查了平行线分线段成比例定理,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(1)两条直线被一组平行线所截,所得的对应线段成比例.
(2)见解析
(3)
【分析】本题考查了平行线分线段成比例定理,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)根据平行线分线段成比例定理解决问题即可;
(2)如图2中,作交于,模仿情况①的方法解决问题即可;
(3)利用梅氏定理即可解决问题.
【详解】(1)解:情况①中的依据是:两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:两条直线被一组平行线所截,所得的对应线段成比例.
(2)作交于,
∴,
∴,
∴,
∴;
(3)∵,,
∴,
∴;
故答案为:.
3.(1)平行线分线段成比例
(2)见解析
【分析】本题考查了平行线分线段成比例质.
(1)根据题意,上述过程中的依据指的是:平行线分线段成比例,两条直线被一组平行线所截,所得的对应线段成比例;
(2)根据平行线分线段成比例,得到,进而得到,得证.
【详解】(1)解:上述过程中的依据指的是:平行线分线段成比例;
故答案为:平行线分线段成比例;
(2)解:该定理的证明过程补充完整如下:
,
,
,
,
即.
4.(1)
(2)AC的长为a.
【分析】(1)过点F作FM∥AC,交BC于点M.根据平行线分线段成比例定理分别找到AE,CE与FM之间的关系,得到它们的比值;
(2)结合(1)中的线段之间的关系,进行求解.
【详解】(1)解:过点F作FM∥AC,交BC于点M,
∵F为AB的中点,
∴M为BC的中点,FM=AC.
∵CD=BC,
∴CM=CD,
∴,
∵FM∥AC,
∴∠CED=∠MFD,∠ECD=∠FMD.
∴△FMD∽△ECD.
∴.
∴.
∴;
(2)解:∵点F是AB的中点,AB=a,
∴FB=AB=a.
∵FB=AE,
∴AE=a.
由(1)知,,
∴AC=AE=×a=a,
即AC的长为a.
【点睛】本题主要考查了平行线分线段成比例定理,相似三角形的判定和性质,作出平行线构造出相似三角形是解本题的关键.
5.(1)
(2)
【分析】本题主要考查梅涅劳斯定理的运用,相似三角形的判定和性质,理解梅涅劳斯定理,掌握构造三角形相似,相似三角形的判定和性质是解题的关键.
(1)根据材料提示的方法计算即可求解;
(2)根据材料提示方法得到,由面积公式得到,由此即可求解.
【详解】(1)解:根据题意可得,,
又∵,
∴,,
∴,
在等边中,,点是的中点,
∴,
∴,
∴;
(2)解:根据题意可得,即,
∴,
如图所示,连接,
∴,
∴,
故答案为:.
6.(1)证明见解析
(2)
(3)
【分析】(1)如图,过点作,交的延长线于点,可知△YBX∽△YAE,△ZCX∽△ZAE,可得,代入进而可证成立;
(2)如图,过点A作AG∥BC,交CF的延长线于点G,由题意可知,,代入求值即可;
(3)如图5,分别过作 ,由题意可知,,,有,,对计算求值即可.
【详解】(1)证明:如图,过点作,交的延长线于点
∴
故可知△YBX∽△YAE,△ZCX∽△ZAE
∴
∵
∴.
(2)解:如图,过点A作AG∥BC,交CF的延长线于点G
∴由题意可知
∵D是BC的中点,为等边三角形
∴,
在中
∵
∴
解得
故答案为:.
(3)解:如图5,分别过作
∵图5同图1,故可知
∵F为AB中点,CD=BC,
∴
∵
∴
∴
∴
∵
∴四边形BCEF的面积为
故答案为:.
【点睛】本题考查了三角形相似,等边三角形的性质,勾股定理等知识.解题的关键在于证明三角形相似.
7.(1)见解析;(2)6
【分析】(1)由题意可得,然后根据比例的性质可进行求证;
(2)由(1)可得,进而由题意易得,,然后可得,则由勾股定理可得,最后问题可求解.
【详解】解:(1)补充的证明过程如下:
,
,
;
(2)根据梅涅劳斯定理得,
∵点D为BC的中点,,
,,
,
∵,,
∴AD⊥BC,BD=5,
∴在中, ,
.
故答案为6.
【点睛】本题主要考查相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
8.(1)平行线分线段成比例
(2)证明过程补充见解析
(3)
(4)
【分析】本题考查了平行线分线段成比例,相似三角形的判定及性质,熟练掌握相似三角形的性质是解答本题的关键.
(1)根据题意,上述过程中的依据指的是:平行线分线段成比例,两条直线被一组平行线所截,所得的对应线段成比例;
(2)根据平行线分线段成比例,得到,进而得到,得证.
(3)根据题意点是的中点,,再由图示三角形的各线段对应关系得到,再由,得到,由此得到答案.
(4)过点作交的延长线于点,由此得到,,由相似三角形的性质得到,,由此得到答案.
【详解】(1)解:上述过程中的依据指的是:平行线分线段成比例
(2)该定理的证明过程补充完整如下:
,
,
即
(3)点是的中点,,
,
,
,即,
,
,
.
(4)如图,过点作交的延长线于点,
,,
,,
,
,,
,
,
,
,
,,
,
,
,
,
.
9.
(1)详见解析;(2);(3)
【分析】(1) 过点作交于点,根据平行线分线段成比例定理列出比例,化简计算即可.
(2) 根据定理,勾股定理,等边三角形的性质解答即可.
(3) 根据定理,计算比值,后解答即可.
【详解】(1)证明:如图,过点作交于点,
则.
故:.
(2)解:如图,根据梅涅劳斯定理得:.
又,
∴,
.
在等边中,,点为的中点,
.
由勾股定理知:
.
(3)解:线段是的梅氏线,
由梅涅劳斯定理得,,
即,则.
如图,连接,
,
于是
.
【点睛】本题考查了平行线分线段成比例定理,勾股定理,等边三角形的性质,三角形面积的计算,熟练掌握定理是解题的关键.
10.见解析
【分析】连接CY、AX ,设A到XZ的距离为h1,C到XZ的距离为h2,再根据“两个三角形等高时面积之比等于底边之比”的性质,分别列出、、,再计算即可.
【详解】证明:如图,连接CY、AX
设A到XZ的距离为h1,C到XZ的距离为h2
∴
∴
【点睛】本题考查了三角形的面积计算,作出辅助线,通过面积写出线段比是解题关键.
模型证明
1)梅涅劳斯定理模型
如图1,如果一条直线与 的三边 或其延长线交于 点,那么
其中:这条直线叫 的梅氏线, 叫梅氏三角形。
证明:
如图2,过点 作 ,交 的延长线于点 ,易证:
2)梅涅劳斯定理的逆定理模型
如图1,若 分别是 的三边 或其延长线的三点,如果
则 三点共线。
证明:假设 三点不共线,直线 与 交于 ,由梅涅劳斯定理得
即 与 重合, 三点共线。
经典题目:
1.请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设,,依次是的三边,,或其延长线上的点,且这三点共线,则满足.
这个定理的证明步骤如下:
情况①:如图1,直线交的边于点,交边于点,交边的延长线与点.
过点作交于点,则,(依据),
∴,
∴,即.
情况②:如图2,直线分别交的边,,的延长线于点,,.…
(1)情况①中的依据指: ;
(2)请你根据情况①的证明思路完成情况②的证明;
(3)如图3,,分别是的边,上的点,且,连接并延长,交的延长线于点,那么
2.请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设D,E,F依次是的三边及其延长线上的点,且这三点共线,则满足.这个定理的证明步骤如下:
情况①:如图1,直线交的边于点D,交边于点E,交边的延长线于点F.过点C作交于点G,
则,(依据)
∴.
∴,
即.
情况②:如图2,直线分别交的边的延长线于点D,E,F…
(1)情况①中的依据指:_______.
(2)请你根据情况①的证明思路完成情况②的证明.
(3)如图3,D、E分别是的边上的点,且,连接并延长,交的延长线于点F,那么______.
3.请阅读下列材料,完成任务.
梅涅劳斯(Menelaus)是公元1世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交(交点不能是三角形的顶点),可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积.该定理被称为梅涅劳斯定理,简称梅氏定理.
如图1,直线交线段于点,交线段于点,交延长线于点D,可截得六条线段,则这六条线段满足,下面是该定理的一部分证明过程:
证明:如图2,过点作,交延长线于点,则有(依据),…
(1)上述过程中的“依据”指的是 ;
(2)请将该定理的证明过程补充完整.
4.小明在网上学习了梅涅劳斯定理之后,编制了下面一个题,请你解答.已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
(1)求的值;
(2)若AB=a,FB=AE,求AC的长.
5.梅涅劳斯()是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与的三边或它们的延长线交于三点,那么一定有.下面是利用相似三角形的有关知识证明该定理的部分过程:证明:如图(2),过点作,交的延长线于点,则有,,.类似的,如图(3),三边的延长线分别交直线于三点,则有:.请利用上述定理的证明方法或结论完成下面问题:
(1)如图(4),等边的边长为,点为的中点,点在上,且,与交于点,求的长.(写出求解过程)
(2)如图(5),的面积为,为中点,延长至,使,连接交于,则四边形的面积为 .(直接写出答案)
6.梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作,交DF的延长线于点G,
则有,,
∴.
请用上述定理的证明方法解决以下问题:
(1)如图(3),△ABC三边CB,AB,AC的延长线分别交直线l于X,Y,Z三点,证明:.
(2)如图(4),等边△ABC的边长为2,点D为BC的中点,点F在AB上,且,CF与AD交于点E,则AE的长为________.
(3)如图(5),△ABC的面积为2,F为AB中点,延长BC至D,使,连接FD交AC于E,则四边形BCEF的面积为________.
7.梅涅劳斯定理
梅涅劳斯()是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作,交DF的延长线于点G,则有.
任务:(1)请你将上述材料中的剩余的证明过程补充完整;
(2)如图(3),在中,,,点D为BC的中点,点F在AB上,且,CF与AD交于点E,则________.
8.请阅读下列材料,并完成相应的任务.
梅涅劳斯()是公元1世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,若一条直线与三角形的三边或其延长线相交(交点不能是三角形的顶点),可以得到六条线段,三条不连续线段的乘积等于剩下三条线段的乘积.该定理被称为梅涅劳斯定理,简称梅氏定理.
如图1,直线交线段于点,交线段于点,交延长线于点,可截得六条线段、、、、、,则这六条线段满足.
下面是该定理的一部分证明过程:
证明:如图2,过点作,交延长线于点
则有(依据),…
(1)上述过程中的依据指的是________;
(2)请将该定理的证明过程补充完整.
(3)在图1中,若点是的中点,,则的值为________;
(4)在图1中,若,,则的值为________.
9.梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图1,如果一条直线与的三边或它们的延长线交于三点,那么一定有.
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图2,过点作,交的延长线于点,则有,,
∴,
.
请用上述定理的证明方法解决以下问题:
(1)如图3,三边的延长线分别交直线于三点,证明:.
请用上述定理的证明方法或结论解决以下问题:
(2)如图4,等边的边长为3,点为的中点,点在上,且与交于点,试求的长.
(3)如图5,的面积为4,F为中点,延长至,使,连接交于,求四边形的面积.
10.如图,三边,,的延长线分别交直线于,,三点,证明:.(即证明梅涅劳斯定理的其中一种形式)
参考答案
1.(1)两条直线被一组平行线所截,所得的对应线段成比例
(2)证明过程见详解
(3)
【分析】(1)根据平行线分线段成比例定理解决问题即可;
(2)如图2中,作交于,模仿情况①的方法解决问题即可;
(3)利用梅氏定理即可解决问题.
【详解】(1)解:情况①中的依据是:两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:两条直线被一组平行线所截,所得的对应线段成比例.
(2)证明:如图2中,作交于,
则有,
∴,
∴,则,变形得,
∴,
∵,
∴,
∴,
∴,
∴.
(3)解:∵,,
∴,
∴.
故答案为:.
【点睛】本题考查了平行线分线段成比例定理,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(1)两条直线被一组平行线所截,所得的对应线段成比例.
(2)见解析
(3)
【分析】本题考查了平行线分线段成比例定理,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)根据平行线分线段成比例定理解决问题即可;
(2)如图2中,作交于,模仿情况①的方法解决问题即可;
(3)利用梅氏定理即可解决问题.
【详解】(1)解:情况①中的依据是:两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:两条直线被一组平行线所截,所得的对应线段成比例.
(2)作交于,
∴,
∴,
∴,
∴;
(3)∵,,
∴,
∴;
故答案为:.
3.(1)平行线分线段成比例
(2)见解析
【分析】本题考查了平行线分线段成比例质.
(1)根据题意,上述过程中的依据指的是:平行线分线段成比例,两条直线被一组平行线所截,所得的对应线段成比例;
(2)根据平行线分线段成比例,得到,进而得到,得证.
【详解】(1)解:上述过程中的依据指的是:平行线分线段成比例;
故答案为:平行线分线段成比例;
(2)解:该定理的证明过程补充完整如下:
,
,
,
,
即.
4.(1)
(2)AC的长为a.
【分析】(1)过点F作FM∥AC,交BC于点M.根据平行线分线段成比例定理分别找到AE,CE与FM之间的关系,得到它们的比值;
(2)结合(1)中的线段之间的关系,进行求解.
【详解】(1)解:过点F作FM∥AC,交BC于点M,
∵F为AB的中点,
∴M为BC的中点,FM=AC.
∵CD=BC,
∴CM=CD,
∴,
∵FM∥AC,
∴∠CED=∠MFD,∠ECD=∠FMD.
∴△FMD∽△ECD.
∴.
∴.
∴;
(2)解:∵点F是AB的中点,AB=a,
∴FB=AB=a.
∵FB=AE,
∴AE=a.
由(1)知,,
∴AC=AE=×a=a,
即AC的长为a.
【点睛】本题主要考查了平行线分线段成比例定理,相似三角形的判定和性质,作出平行线构造出相似三角形是解本题的关键.
5.(1)
(2)
【分析】本题主要考查梅涅劳斯定理的运用,相似三角形的判定和性质,理解梅涅劳斯定理,掌握构造三角形相似,相似三角形的判定和性质是解题的关键.
(1)根据材料提示的方法计算即可求解;
(2)根据材料提示方法得到,由面积公式得到,由此即可求解.
【详解】(1)解:根据题意可得,,
又∵,
∴,,
∴,
在等边中,,点是的中点,
∴,
∴,
∴;
(2)解:根据题意可得,即,
∴,
如图所示,连接,
∴,
∴,
故答案为:.
6.(1)证明见解析
(2)
(3)
【分析】(1)如图,过点作,交的延长线于点,可知△YBX∽△YAE,△ZCX∽△ZAE,可得,代入进而可证成立;
(2)如图,过点A作AG∥BC,交CF的延长线于点G,由题意可知,,代入求值即可;
(3)如图5,分别过作 ,由题意可知,,,有,,对计算求值即可.
【详解】(1)证明:如图,过点作,交的延长线于点
∴
故可知△YBX∽△YAE,△ZCX∽△ZAE
∴
∵
∴.
(2)解:如图,过点A作AG∥BC,交CF的延长线于点G
∴由题意可知
∵D是BC的中点,为等边三角形
∴,
在中
∵
∴
解得
故答案为:.
(3)解:如图5,分别过作
∵图5同图1,故可知
∵F为AB中点,CD=BC,
∴
∵
∴
∴
∴
∵
∴四边形BCEF的面积为
故答案为:.
【点睛】本题考查了三角形相似,等边三角形的性质,勾股定理等知识.解题的关键在于证明三角形相似.
7.(1)见解析;(2)6
【分析】(1)由题意可得,然后根据比例的性质可进行求证;
(2)由(1)可得,进而由题意易得,,然后可得,则由勾股定理可得,最后问题可求解.
【详解】解:(1)补充的证明过程如下:
,
,
;
(2)根据梅涅劳斯定理得,
∵点D为BC的中点,,
,,
,
∵,,
∴AD⊥BC,BD=5,
∴在中, ,
.
故答案为6.
【点睛】本题主要考查相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
8.(1)平行线分线段成比例
(2)证明过程补充见解析
(3)
(4)
【分析】本题考查了平行线分线段成比例,相似三角形的判定及性质,熟练掌握相似三角形的性质是解答本题的关键.
(1)根据题意,上述过程中的依据指的是:平行线分线段成比例,两条直线被一组平行线所截,所得的对应线段成比例;
(2)根据平行线分线段成比例,得到,进而得到,得证.
(3)根据题意点是的中点,,再由图示三角形的各线段对应关系得到,再由,得到,由此得到答案.
(4)过点作交的延长线于点,由此得到,,由相似三角形的性质得到,,由此得到答案.
【详解】(1)解:上述过程中的依据指的是:平行线分线段成比例
(2)该定理的证明过程补充完整如下:
,
,
即
(3)点是的中点,,
,
,
,即,
,
,
.
(4)如图,过点作交的延长线于点,
,,
,,
,
,,
,
,
,
,
,,
,
,
,
,
.
9.
(1)详见解析;(2);(3)
【分析】(1) 过点作交于点,根据平行线分线段成比例定理列出比例,化简计算即可.
(2) 根据定理,勾股定理,等边三角形的性质解答即可.
(3) 根据定理,计算比值,后解答即可.
【详解】(1)证明:如图,过点作交于点,
则.
故:.
(2)解:如图,根据梅涅劳斯定理得:.
又,
∴,
.
在等边中,,点为的中点,
.
由勾股定理知:
.
(3)解:线段是的梅氏线,
由梅涅劳斯定理得,,
即,则.
如图,连接,
,
于是
.
【点睛】本题考查了平行线分线段成比例定理,勾股定理,等边三角形的性质,三角形面积的计算,熟练掌握定理是解题的关键.
10.见解析
【分析】连接CY、AX ,设A到XZ的距离为h1,C到XZ的距离为h2,再根据“两个三角形等高时面积之比等于底边之比”的性质,分别列出、、,再计算即可.
【详解】证明:如图,连接CY、AX
设A到XZ的距离为h1,C到XZ的距离为h2
∴
∴
【点睛】本题考查了三角形的面积计算,作出辅助线,通过面积写出线段比是解题关键.
同课章节目录
