6.2.2用坐标表示平移同步练习题(含答案)
文档属性
| 名称 | 6.2.2用坐标表示平移同步练习题(含答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 62.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-28 00:00:00 | ||
图片预览

文档简介
6.2.2用坐标表示平移
夯基达标
1.填空
⑴在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x﹢a,y)(或 ),将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y﹢b)(或 )。
⑵在平面直角坐标系中,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;如果把一个图形各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
2.在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
3.将点A(4,3)向 平移 个单位长度后,其坐标的变化是( 6, 3 ) 。
4.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.
5. 已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为______,________.
6.△ABC中,如果A(1,1),B(-1,-1),C(2,-1),则△ABC的面积为________.
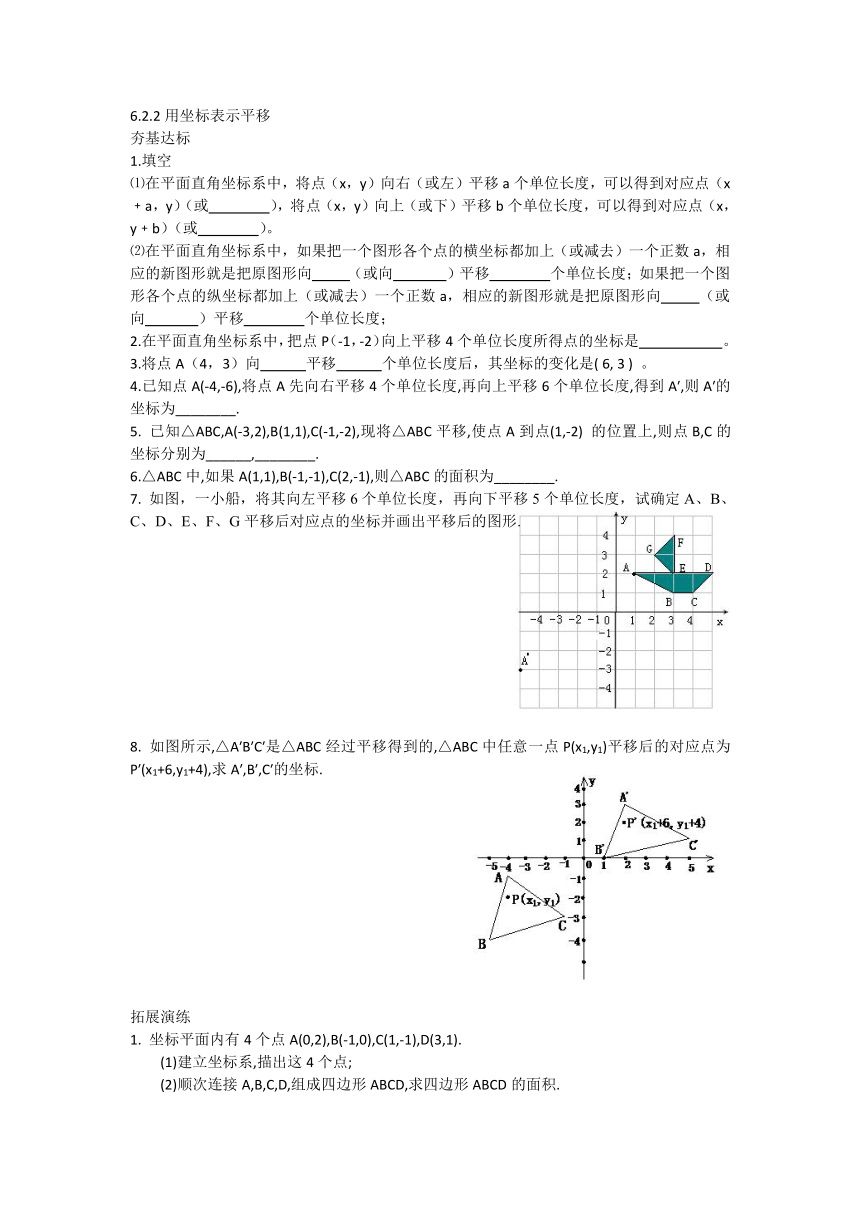
7. 如图,一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A、B、C、D、E、F、G平移后对应点的坐标并画出平移后的图形.
8. 如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′,C′的坐标.
拓展演练
1. 坐标平面内有4个点A(0,2),B(-1,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
2. 如图所示,△BCO是△BAO经过某种变换得到的,则图中A与C 的坐标之间的关系是什么 如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么
3.在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB 中点的坐标与点A,B的坐标之间有什么关系 对线段AC中点和点A,C及线段CD中点和点C,D成立吗
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标.
聚焦中考
1.(2009,哈尔滨)如图,在每个小正方形的边长均为1个单位
长度的方格纸中,有一个△ABC,△ABC的顶点与小正方形的顶
点重合.在方格纸中,将△ABC向下平移5个单位长度,向右
平移3各单位长度得到△A1B1C1,请画出△A1B1C1
2. 如图.直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,一1),则△ABC的面积为_____平方单位.
6.2.2用坐标表示平移
夯基达标
1.⑴(x﹣a,y) (x,y﹣b)
⑵右 左 a 上 下 a
2.(﹣1,2) 3.右 2
4.(0,0) 5. (5,-3) (3,-6) 6.3
7. 把小船向右平移6个单位长度,再向下平移
5个单位长度,先确定关键点A、B、C、D、
E、F、G,并把关键点分别向右平移6个单位
长度,向下平移5个单位长度.根据点的坐标的
变化规律,由A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),F(3,4),G(2,3)可得平移后对应点为A′(-5,-3),B′(-3,-4)、C′(-2,-4)、D′(-1,-3)、E′(-3,-3)、F′(-3,-1)、G′(-4,-2).描出这些对应点并按原来的顺次连结起来,可得平移后图形,如图。
8. A′(2,3),B′(1,0),C′(5,1)
拓展演练
1. (1)略 (2)四边形ABCD的面积为6.5.
2. A与C的横坐标相同,纵坐标互为相反数,N点的坐标为(x,-y).
3. 提示:(1)线段AB中点的坐标为(,0),即(3,0);对AC中点和点A,C 及线段CD中点和点C,D都成立. (2)线段MN的中点P的坐标为(,0)
聚焦中考
1.如图:
2. 5
夯基达标
1.填空
⑴在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x﹢a,y)(或 ),将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y﹢b)(或 )。
⑵在平面直角坐标系中,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;如果把一个图形各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
2.在平面直角坐标系中,把点P(-1,-2)向上平移4个单位长度所得点的坐标是 。
3.将点A(4,3)向 平移 个单位长度后,其坐标的变化是( 6, 3 ) 。
4.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.
5. 已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,-2) 的位置上,则点B,C的坐标分别为______,________.
6.△ABC中,如果A(1,1),B(-1,-1),C(2,-1),则△ABC的面积为________.
7. 如图,一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A、B、C、D、E、F、G平移后对应点的坐标并画出平移后的图形.
8. 如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′,C′的坐标.
拓展演练
1. 坐标平面内有4个点A(0,2),B(-1,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
2. 如图所示,△BCO是△BAO经过某种变换得到的,则图中A与C 的坐标之间的关系是什么 如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么
3.在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB 中点的坐标与点A,B的坐标之间有什么关系 对线段AC中点和点A,C及线段CD中点和点C,D成立吗
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标.
聚焦中考
1.(2009,哈尔滨)如图,在每个小正方形的边长均为1个单位
长度的方格纸中,有一个△ABC,△ABC的顶点与小正方形的顶
点重合.在方格纸中,将△ABC向下平移5个单位长度,向右
平移3各单位长度得到△A1B1C1,请画出△A1B1C1
2. 如图.直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,一1),则△ABC的面积为_____平方单位.
6.2.2用坐标表示平移
夯基达标
1.⑴(x﹣a,y) (x,y﹣b)
⑵右 左 a 上 下 a
2.(﹣1,2) 3.右 2
4.(0,0) 5. (5,-3) (3,-6) 6.3
7. 把小船向右平移6个单位长度,再向下平移
5个单位长度,先确定关键点A、B、C、D、
E、F、G,并把关键点分别向右平移6个单位
长度,向下平移5个单位长度.根据点的坐标的
变化规律,由A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),F(3,4),G(2,3)可得平移后对应点为A′(-5,-3),B′(-3,-4)、C′(-2,-4)、D′(-1,-3)、E′(-3,-3)、F′(-3,-1)、G′(-4,-2).描出这些对应点并按原来的顺次连结起来,可得平移后图形,如图。
8. A′(2,3),B′(1,0),C′(5,1)
拓展演练
1. (1)略 (2)四边形ABCD的面积为6.5.
2. A与C的横坐标相同,纵坐标互为相反数,N点的坐标为(x,-y).
3. 提示:(1)线段AB中点的坐标为(,0),即(3,0);对AC中点和点A,C 及线段CD中点和点C,D都成立. (2)线段MN的中点P的坐标为(,0)
聚焦中考
1.如图:
2. 5
