苏科版七年级数学下册期中考试综合质量检测卷一(含解析)
文档属性
| 名称 | 苏科版七年级数学下册期中考试综合质量检测卷一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 17:13:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏科版七年级数学下册期中考试综合质量检测卷一
一、选择题(共30分)
1.(3分)如图,将绕点B顺时针旋转角,得到,此时点A,点B,点在一条直线上,若,则旋转角=( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A. B. C. D.
3.(3分)已知,则的值为( )
A.9 B.10 C.12 D.15
4.(3分)下列关于体育运动的图标中,为轴对称图形的是( )
A. B. C. D.
5.(3分)下面的左面图形平移后可以得到右面图形的是( )
A. B. C. D.
6.(3分)一房屋的结构示意图如图所示(单位:),这家主人打算把卧室以外的部分都铺上地砖,至少需要地砖( )
A. B. C. D.
7.(3分)边长分别为和的两个正方形按如图所示的位置摆放,则图中的阴影部分的面积为( ).
A. B. C. D.
8.(3分)下列算式中,计算结果是的是( )
A. B. C. D.
9.(3分)若(其中为正整数),则的值分别为( )
A.30,10 B.3,11 C.15,10 D.10,10
10.(3分)已知,若a,b都是整数,则的值不可能是( )
A.1 B. C. D.
二、填空题(共24分)
11.(3分)有下列现象:时针的转动;摩天轮的转动;地下水位逐年下降;传送带上的机器人其中,属于旋转的是 .
12.(3分)如图,在长为15米,宽为10米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为1米,其他部分均种植花草,则种植花草的面积是 平方米.
13.(3分)长方形的长为,宽为,则它的面积为 .
14.(3分)已知,则 .
15.(3分)若,则的值为 .
16.(3分)已知,则的值为 .
17.(3分)杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一,比法国数学家帕斯卡发现这一规律要早约400年.观察下列各式及其展开式,请写出展开式中的第三项 .
18.(3分)如图,在直角中,,,,,D、E、F分别是、、边上的动点,则的最小值是 .
三、解答题(共66分)
19.(4分)已知(是正整数),求的值.
20.(4分)先化简,再求值:,其中,
21.(7分)(1)若,求的值.
(2)若,求值.
22.(7分)已知一个长方体包装箱的长为,宽为,高为.
(1)求这个长方体包装箱的体积;
(2)如果给这个长方体包装箱的外表面都喷上油漆,那么需喷油漆的面积为多少平方米?
23.(7分)某学校开垦了两块园地当作学生劳动实践活动基地.两块园地中,一块是长方形,另一块是正方形.春季学生在这两块园地内种植同一种蔬菜,若长方形园地每排种植株,种植了排,正方形园地每排种植株,种植了排().
(1)请计算长方形园地种植的蔬菜比正方形园地种植的蔬菜多多少株.
(2)当,时,这两块园地一共种植了多少株蔬菜?
24.(7分)2025年2月10日,南水北调东线一期工程正式启动本年度调水工作,计划向黄河以北调水1.51亿立方米.如图,某段河道的横截面是梯形,已知上底的长度为,下底的长度为,河道的最大高度为.
(1)求河道横截面的面积;
(2)经测量得出,那么长的南水北调的河道最多可以蓄水多少立方米?(棱柱的体积棱柱的底面积高)
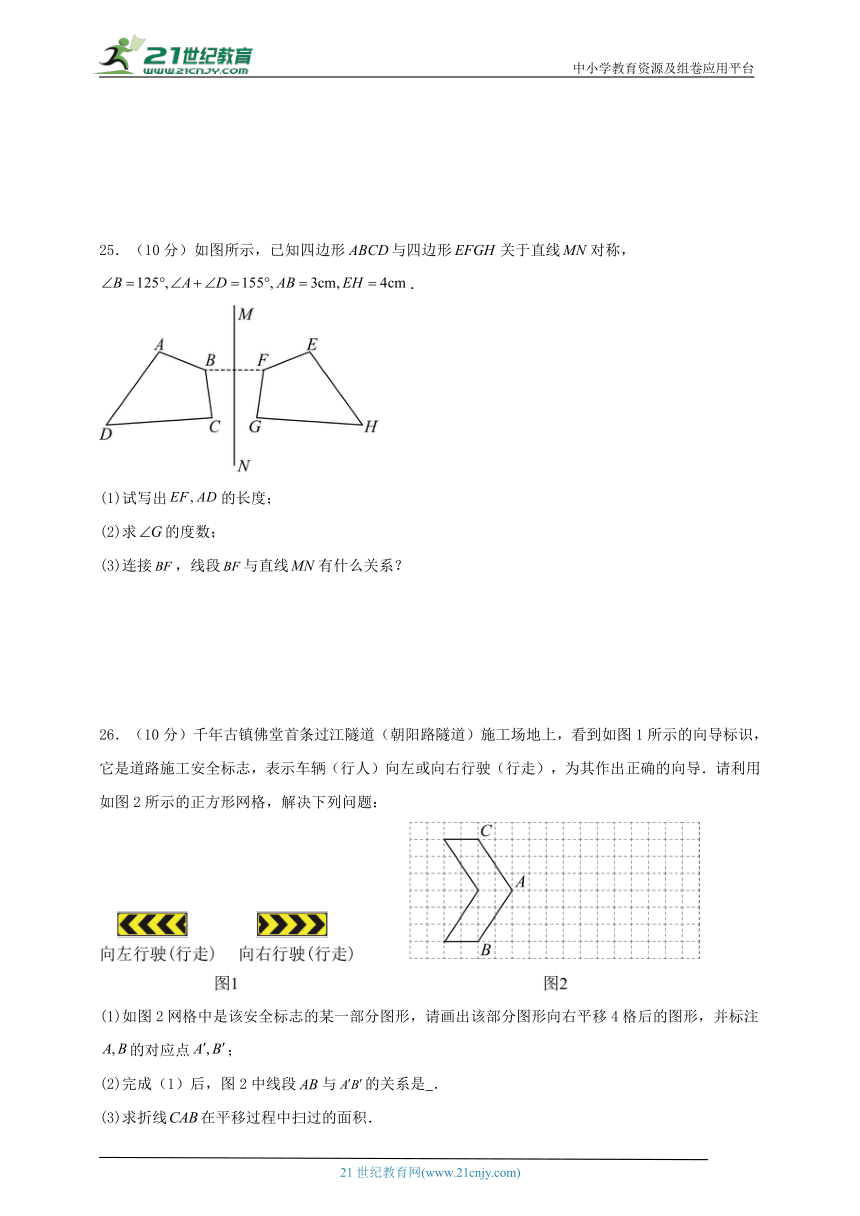
25.(10分)如图所示,已知四边形与四边形关于直线对称,.
(1)试写出的长度;
(2)求的度数;
(3)连接,线段与直线有什么关系?
26.(10分)千年古镇佛堂首条过江隧道(朝阳路隧道)施工场地上,看到如图1所示的向导标识,它是道路施工安全标志,表示车辆(行人)向左或向右行驶(行走),为其作出正确的向导.请利用如图2所示的正方形网格,解决下列问题:
(1)如图2网格中是该安全标志的某一部分图形,请画出该部分图形向右平移4格后的图形,并标注的对应点;
(2)完成(1)后,图2中线段与的关系是 .
(3)求折线在平移过程中扫过的面积.
27.(10分)如图,点O为直线上一点,过点O作射线,使得,将一个含有角的直角三角板的直角顶点放在点O处,使边在射线上,另一边在直线的下方,将图中的三角板绕点O按顺时针方向旋转.
(1)在三角板旋转的过程中,当时,三角板旋转的角度为________;
(2)当所在的射线恰好平分时,三角板旋转的角度为________;
(3)若三角板绕点O按每秒的速度顺时针旋转,同时射线绕点O按每秒的速度顺时针旋转,当与射线重合时,同时停止运动,请计算三角板的直角边所在射线恰好平分时,三角板运动的时间.
参考答案
1.D
【分析】本题考查旋转变换的性质,解题的关键是理解题意,灵活运用所学知识解决问题.先根据角度的和差得出,再利用旋转变换的性质求解即可.
【详解】解:∵,
∴,
∴,
∴,即旋转角.
故选:D.
2.D
【分析】本题考查的是积的乘方运算,根据计算即可.
【详解】解:A.,错误;
B.,错误;
C.,错误.
D. ,正确,
故选D.
3.A
【分析】本题主要考查平方差公式:,直接平方差公式求出即可.熟记公式结构是解题的关键.
【详解】解:,,
.
故选:A.
4.C
【分析】本题考查的是轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
根据轴对称图形的概念判断即可.
【详解】解:A、图标不属于轴对称图形,故此选项不符合题意;
B、图标不属于轴对称图形,故此选项不符合题意;
C、图标属于轴对称图形,故此选项符合题意;
D、图标不属于轴对称图形,故此选项不符合题意.
故选:C.
5.D
【分析】本题考查图形的平移变换.注意平移不改变图形的形状和大小,属于基础题,一定要熟记平移的性质及特点.
根据平移的性质,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,即可判断出答案.
【详解】A、两个图形大小不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
B、两个图形大小不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
C、两个图形箭头方向不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
D、左面的图形平移后可以得到右面图形,故本选项符合题意.
故选D.
6.A
【分析】本题主要考查了单项式乘以单项式和单项式乘以多项式在几何图形中的应用,根据长方形面积公式分别求出厨房,客厅,卫生间的面积,再把三者的面积求和即可得到答案.
【详解】解:
,
∴至少需要地砖,
故选:A.
7.A
【分析】本题主要考查了整式的运算的应用,关键是用代数式表示出阴影部分的面积.
根据已知图形得出阴影部分的面积是:,求出结果即可得解.
【详解】解:阴影部分的面积是:
,
,
,
故选:A.
8.B
【分析】本题考查了积的乘方,同底数幂的除法,合并同类项,零指数幂,根据积的乘方,同底数幂的除法,合并同类项,零指数幂的定义逐项计算判断即可.
【详解】解:A、,故本选项不符合题意;
B、,本选项符合题意;
C、与不是同类项,不可以合并,故本选项不符合题意;
D、,故本选项不符合题意,
故选:B.
9.B
【分析】本题考查了同底数幂的乘法,科学记数法的计算,根据同底数幂的乘法运算法则进行计算即可.
【详解】解:,
,
故选:B.
10.D
【分析】此题考查了多项式乘多项式,根据多项式乘多项式的乘法法则,得到,,再根据和为整数,进行分类讨论是解题的关键.
【详解】∵,
∴,
则,,
∵和均为整数,
∴当时,,此时;
当时,,此时;
当时,,此时;
当时,,此时;
综上:或,
故选:D.
11.
【分析】本题考查了图形的旋转,旋转是在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,解决本题的关键是根据旋转的定义进行判断即可.
【详解】解:时针的转动属于旋转;
摩天轮的转动属于旋转;
地下水位逐年下降属于平移,不是旋转;
传送带上的机器人属于平移,不是旋转.
故答案为: .
12.126
【分析】本题主要考查了平移的性质,可以根据平移的性质得到道路的面积等于横纵小路的面积减去小路交叉处的面积,再用长方形地块的面积减去道路的面积即可得到答案.
【详解】解:平方米,
∴种植花草的面积是126平方米,
故答案为:126.
13.
【分析】本题考查单项式乘单项式的应用,根据面积等于长乘宽列式计算即可.
【详解】解:∵长方形的长为,宽为,
∴它的面积为:,
故答案为:.
14.
【分析】本题考查了同底数幂的除法法则,利用幂的乘方变形得出同底数幂的乘法是解题关键.根据幂的乘方变形,再根据同底数幂的除法进行计算,最后代入求出即可.
【详解】解:由,得,
,
故答案为:.
15./
【分析】本题考查积的乘方逆用,非负数的性质,解题的关键是掌握幂的运算法则.根据绝对值和平方式的非负性求出x和y的值,再逆用积的乘方运算法则进行计算.
【详解】解:∵,,且,
∴,,
解得:,,
∴.
故答案是:.
16.81
【分析】本题考查了同底数幂的乘法,根据已知得到,进而得到,求出结果即可.
【详解】解:,
,
,
故答案为:81.
17.
【分析】本题考查了杨辉三角,正确得出杨辉三角的规律是解题的关键.每个单项式的次数都等于左边式子的次数,第一个单项式的底数为a,各项是按a的降幂,b的升幂排列的,系数依次为杨辉三角中的数,依此规律写出即可;
【详解】解:由题意得,
所以展开式中的第三项是,
故答案为:
18.9.6
【分析】本题考查了轴对称路径最短问题,作关于直线的对称点,作关于直线的对称点,连接,,,,,,.,推出,可得、、共线,由,,可知、、、共线时,且时,的值最小,最小值,求出的值即可解决问题理解转化思想是解题的关键.
【详解】解:如图作关于直线的对称点,作关于直线的对称点,连接,,,,,,.
∴
,,,
,
、、共线,
,
,
当、、、共线时,且时,的值最小,最小值,
,
,
∴的最小值为9.6.
故答案为:9.6.
19.2048
【分析】本题主要考查同底数幂乘法的逆用,熟练掌握运算法则是解题的关键.根据题意得到,即可得到答案.
【详解】解:,
.
20.,
【分析】本题主要考查了整式的化简求值,先计算积的乘方,再计算单项式乘以多项式,然后合并同类项化简,最后代值计算即可.
【详解】解:
,
当,时,原式.
21.(1)
(2)或
【分析】此题考查了幂的乘方,同底数幂的除法的逆运算,代数式求值,解题的关键是掌握以上运算法则.
(1)根据幂的乘方,同底数幂的除法的逆运算将变形为,然后代入求解即可;
(2)根据幂的乘方的逆运算得到,,然后求出,然后代入求解即可.
【详解】解:(1)∵,
;
(2)∵,
∴,
∴或.
22.(1);
(2).
【分析】本题考查单项式的乘法的应用、列代数式,涉及单项式乘单项式、单项式乘多项式,理解题意,掌握单项式乘法运算法则是解答的关键.
(1)先利用长方体的体积公式列代数式,再利用单项式乘单项式的运算法则求解即可;
(2)先利用长方体的表面积公式列出代数式,再利用单项式乘多项式的运算法则求解即可.
【详解】(1)解:因为,
所以这个长方体包装箱的体积为;
(2)解:因为包装箱的表面积为,
所以需喷的油漆.
23.(1)多株;
(2)株.
【分析】本题考查了多项式乘以多项式,完全平方公式,合并同类项,熟练掌握运算法则是解题的关键.
()根据题意列式并化简计算即可;
()先根据题意列式并化简计算,然后把,代入求值即可.
【详解】(1)解:由题意得
,
答:长方形园地种植的蔬菜比正方形园地种植的蔬菜多株;
(2)解:由题意得
;
当,时,
原式
(株),
答:当,时,这两块园地一共种植了株蔬菜.
24.(1)
(2)
【分析】本题考查了整式的混合运算,代数式求值,掌握整式混合运算的法则是解题的关键.
(1)根据梯形的面积公式列出代数式,然后根据整式的混合运算法则进行计算即可;
(2)先代入求出梯形面积,再根据棱柱的体积公式列出代数式,然后根据整式的混合运算法则进行计算即可.
【详解】(1)解:河道横截面的面积为:
;
(2)当时,
,
,
答:长的南水北调的河道最多可以蓄水.
25.(1)
(2)
(3)直线垂直平分
【分析】本题考查的是轴对称的性质,理解轴对称的含义是解本题的关键;
(1)根据四边形与四边形关于直线对称,可得对应边相等,从而可得答案;
(2)先求解,再根据轴对称的性质可得答案;
(3)根据对称轴垂直平分对称点的连线,可得答案;
【详解】(1)解:∵四边形与四边形关于直线对称.,
∴;
(2)解:∵,
∴,
由轴对称的性质可得:
;
(3)解:∵对称轴垂直平分对称点的连线,
∴直线垂直平分.
26.(1)见解析
(2)平行且相等
(3)24
【分析】本题考查了平移作图以及平移的性质,熟练掌握平移的性质是解题的关键;
(1)根据平移的性质,画出该部分图形向右平移4格后的图形,即可求解;
(2)根据平移的性质即可求解;
(3)根据2个平行四边形的面积和,即可求解.
【详解】(1)解:如图所示,
(2)根据平移的性质可得:与平行且相等
故答案为:平行且相等.
(3)折线在平移过程中扫过的面积为四边形.
27.(1)
(2)
(3)秒或秒
【分析】(1)根据,求出旋转角即可;
(2)根据,利用补角性质求出,根据所在的射线恰好平分,得出,再求出旋转角即可;
(3)设三角板运动的时间为t秒,当平分时,根据的一半与旋转角相等,列方程,当平分时,根据的一半与旋转角相等,列方程,解方程即可.
【详解】(1)解:∵在射线上,三角板绕点О按顺时针方向旋转,,
旋转角,
三角板旋转的角度为,
故答案为:;
(2)解:∵,
∴,
∵所在的射线恰好平分,
∴,
∴旋转角,
故答案为:;
(3)解:设三角板运动的时间为t秒,则,,
当平分时,,如图:
,
解得;
当平分时,,如图:
,
解得;
综上可知,三角板运动的时间为秒或秒.
【点睛】本题考查旋转的性质,补角的性质,角平分线定义,图形中的角度计算,一元一次方程的应用,熟练运用分类讨论思想是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
苏科版七年级数学下册期中考试综合质量检测卷一
一、选择题(共30分)
1.(3分)如图,将绕点B顺时针旋转角,得到,此时点A,点B,点在一条直线上,若,则旋转角=( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A. B. C. D.
3.(3分)已知,则的值为( )
A.9 B.10 C.12 D.15
4.(3分)下列关于体育运动的图标中,为轴对称图形的是( )
A. B. C. D.
5.(3分)下面的左面图形平移后可以得到右面图形的是( )
A. B. C. D.
6.(3分)一房屋的结构示意图如图所示(单位:),这家主人打算把卧室以外的部分都铺上地砖,至少需要地砖( )
A. B. C. D.
7.(3分)边长分别为和的两个正方形按如图所示的位置摆放,则图中的阴影部分的面积为( ).
A. B. C. D.
8.(3分)下列算式中,计算结果是的是( )
A. B. C. D.
9.(3分)若(其中为正整数),则的值分别为( )
A.30,10 B.3,11 C.15,10 D.10,10
10.(3分)已知,若a,b都是整数,则的值不可能是( )
A.1 B. C. D.
二、填空题(共24分)
11.(3分)有下列现象:时针的转动;摩天轮的转动;地下水位逐年下降;传送带上的机器人其中,属于旋转的是 .
12.(3分)如图,在长为15米,宽为10米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为1米,其他部分均种植花草,则种植花草的面积是 平方米.
13.(3分)长方形的长为,宽为,则它的面积为 .
14.(3分)已知,则 .
15.(3分)若,则的值为 .
16.(3分)已知,则的值为 .
17.(3分)杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一,比法国数学家帕斯卡发现这一规律要早约400年.观察下列各式及其展开式,请写出展开式中的第三项 .
18.(3分)如图,在直角中,,,,,D、E、F分别是、、边上的动点,则的最小值是 .
三、解答题(共66分)
19.(4分)已知(是正整数),求的值.
20.(4分)先化简,再求值:,其中,
21.(7分)(1)若,求的值.
(2)若,求值.
22.(7分)已知一个长方体包装箱的长为,宽为,高为.
(1)求这个长方体包装箱的体积;
(2)如果给这个长方体包装箱的外表面都喷上油漆,那么需喷油漆的面积为多少平方米?
23.(7分)某学校开垦了两块园地当作学生劳动实践活动基地.两块园地中,一块是长方形,另一块是正方形.春季学生在这两块园地内种植同一种蔬菜,若长方形园地每排种植株,种植了排,正方形园地每排种植株,种植了排().
(1)请计算长方形园地种植的蔬菜比正方形园地种植的蔬菜多多少株.
(2)当,时,这两块园地一共种植了多少株蔬菜?
24.(7分)2025年2月10日,南水北调东线一期工程正式启动本年度调水工作,计划向黄河以北调水1.51亿立方米.如图,某段河道的横截面是梯形,已知上底的长度为,下底的长度为,河道的最大高度为.
(1)求河道横截面的面积;
(2)经测量得出,那么长的南水北调的河道最多可以蓄水多少立方米?(棱柱的体积棱柱的底面积高)
25.(10分)如图所示,已知四边形与四边形关于直线对称,.
(1)试写出的长度;
(2)求的度数;
(3)连接,线段与直线有什么关系?
26.(10分)千年古镇佛堂首条过江隧道(朝阳路隧道)施工场地上,看到如图1所示的向导标识,它是道路施工安全标志,表示车辆(行人)向左或向右行驶(行走),为其作出正确的向导.请利用如图2所示的正方形网格,解决下列问题:
(1)如图2网格中是该安全标志的某一部分图形,请画出该部分图形向右平移4格后的图形,并标注的对应点;
(2)完成(1)后,图2中线段与的关系是 .
(3)求折线在平移过程中扫过的面积.
27.(10分)如图,点O为直线上一点,过点O作射线,使得,将一个含有角的直角三角板的直角顶点放在点O处,使边在射线上,另一边在直线的下方,将图中的三角板绕点O按顺时针方向旋转.
(1)在三角板旋转的过程中,当时,三角板旋转的角度为________;
(2)当所在的射线恰好平分时,三角板旋转的角度为________;
(3)若三角板绕点O按每秒的速度顺时针旋转,同时射线绕点O按每秒的速度顺时针旋转,当与射线重合时,同时停止运动,请计算三角板的直角边所在射线恰好平分时,三角板运动的时间.
参考答案
1.D
【分析】本题考查旋转变换的性质,解题的关键是理解题意,灵活运用所学知识解决问题.先根据角度的和差得出,再利用旋转变换的性质求解即可.
【详解】解:∵,
∴,
∴,
∴,即旋转角.
故选:D.
2.D
【分析】本题考查的是积的乘方运算,根据计算即可.
【详解】解:A.,错误;
B.,错误;
C.,错误.
D. ,正确,
故选D.
3.A
【分析】本题主要考查平方差公式:,直接平方差公式求出即可.熟记公式结构是解题的关键.
【详解】解:,,
.
故选:A.
4.C
【分析】本题考查的是轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
根据轴对称图形的概念判断即可.
【详解】解:A、图标不属于轴对称图形,故此选项不符合题意;
B、图标不属于轴对称图形,故此选项不符合题意;
C、图标属于轴对称图形,故此选项符合题意;
D、图标不属于轴对称图形,故此选项不符合题意.
故选:C.
5.D
【分析】本题考查图形的平移变换.注意平移不改变图形的形状和大小,属于基础题,一定要熟记平移的性质及特点.
根据平移的性质,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,即可判断出答案.
【详解】A、两个图形大小不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
B、两个图形大小不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
C、两个图形箭头方向不一样,左面的图形不能通过平移得到右面图形,故本选项不符合题意;
D、左面的图形平移后可以得到右面图形,故本选项符合题意.
故选D.
6.A
【分析】本题主要考查了单项式乘以单项式和单项式乘以多项式在几何图形中的应用,根据长方形面积公式分别求出厨房,客厅,卫生间的面积,再把三者的面积求和即可得到答案.
【详解】解:
,
∴至少需要地砖,
故选:A.
7.A
【分析】本题主要考查了整式的运算的应用,关键是用代数式表示出阴影部分的面积.
根据已知图形得出阴影部分的面积是:,求出结果即可得解.
【详解】解:阴影部分的面积是:
,
,
,
故选:A.
8.B
【分析】本题考查了积的乘方,同底数幂的除法,合并同类项,零指数幂,根据积的乘方,同底数幂的除法,合并同类项,零指数幂的定义逐项计算判断即可.
【详解】解:A、,故本选项不符合题意;
B、,本选项符合题意;
C、与不是同类项,不可以合并,故本选项不符合题意;
D、,故本选项不符合题意,
故选:B.
9.B
【分析】本题考查了同底数幂的乘法,科学记数法的计算,根据同底数幂的乘法运算法则进行计算即可.
【详解】解:,
,
故选:B.
10.D
【分析】此题考查了多项式乘多项式,根据多项式乘多项式的乘法法则,得到,,再根据和为整数,进行分类讨论是解题的关键.
【详解】∵,
∴,
则,,
∵和均为整数,
∴当时,,此时;
当时,,此时;
当时,,此时;
当时,,此时;
综上:或,
故选:D.
11.
【分析】本题考查了图形的旋转,旋转是在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,解决本题的关键是根据旋转的定义进行判断即可.
【详解】解:时针的转动属于旋转;
摩天轮的转动属于旋转;
地下水位逐年下降属于平移,不是旋转;
传送带上的机器人属于平移,不是旋转.
故答案为: .
12.126
【分析】本题主要考查了平移的性质,可以根据平移的性质得到道路的面积等于横纵小路的面积减去小路交叉处的面积,再用长方形地块的面积减去道路的面积即可得到答案.
【详解】解:平方米,
∴种植花草的面积是126平方米,
故答案为:126.
13.
【分析】本题考查单项式乘单项式的应用,根据面积等于长乘宽列式计算即可.
【详解】解:∵长方形的长为,宽为,
∴它的面积为:,
故答案为:.
14.
【分析】本题考查了同底数幂的除法法则,利用幂的乘方变形得出同底数幂的乘法是解题关键.根据幂的乘方变形,再根据同底数幂的除法进行计算,最后代入求出即可.
【详解】解:由,得,
,
故答案为:.
15./
【分析】本题考查积的乘方逆用,非负数的性质,解题的关键是掌握幂的运算法则.根据绝对值和平方式的非负性求出x和y的值,再逆用积的乘方运算法则进行计算.
【详解】解:∵,,且,
∴,,
解得:,,
∴.
故答案是:.
16.81
【分析】本题考查了同底数幂的乘法,根据已知得到,进而得到,求出结果即可.
【详解】解:,
,
,
故答案为:81.
17.
【分析】本题考查了杨辉三角,正确得出杨辉三角的规律是解题的关键.每个单项式的次数都等于左边式子的次数,第一个单项式的底数为a,各项是按a的降幂,b的升幂排列的,系数依次为杨辉三角中的数,依此规律写出即可;
【详解】解:由题意得,
所以展开式中的第三项是,
故答案为:
18.9.6
【分析】本题考查了轴对称路径最短问题,作关于直线的对称点,作关于直线的对称点,连接,,,,,,.,推出,可得、、共线,由,,可知、、、共线时,且时,的值最小,最小值,求出的值即可解决问题理解转化思想是解题的关键.
【详解】解:如图作关于直线的对称点,作关于直线的对称点,连接,,,,,,.
∴
,,,
,
、、共线,
,
,
当、、、共线时,且时,的值最小,最小值,
,
,
∴的最小值为9.6.
故答案为:9.6.
19.2048
【分析】本题主要考查同底数幂乘法的逆用,熟练掌握运算法则是解题的关键.根据题意得到,即可得到答案.
【详解】解:,
.
20.,
【分析】本题主要考查了整式的化简求值,先计算积的乘方,再计算单项式乘以多项式,然后合并同类项化简,最后代值计算即可.
【详解】解:
,
当,时,原式.
21.(1)
(2)或
【分析】此题考查了幂的乘方,同底数幂的除法的逆运算,代数式求值,解题的关键是掌握以上运算法则.
(1)根据幂的乘方,同底数幂的除法的逆运算将变形为,然后代入求解即可;
(2)根据幂的乘方的逆运算得到,,然后求出,然后代入求解即可.
【详解】解:(1)∵,
;
(2)∵,
∴,
∴或.
22.(1);
(2).
【分析】本题考查单项式的乘法的应用、列代数式,涉及单项式乘单项式、单项式乘多项式,理解题意,掌握单项式乘法运算法则是解答的关键.
(1)先利用长方体的体积公式列代数式,再利用单项式乘单项式的运算法则求解即可;
(2)先利用长方体的表面积公式列出代数式,再利用单项式乘多项式的运算法则求解即可.
【详解】(1)解:因为,
所以这个长方体包装箱的体积为;
(2)解:因为包装箱的表面积为,
所以需喷的油漆.
23.(1)多株;
(2)株.
【分析】本题考查了多项式乘以多项式,完全平方公式,合并同类项,熟练掌握运算法则是解题的关键.
()根据题意列式并化简计算即可;
()先根据题意列式并化简计算,然后把,代入求值即可.
【详解】(1)解:由题意得
,
答:长方形园地种植的蔬菜比正方形园地种植的蔬菜多株;
(2)解:由题意得
;
当,时,
原式
(株),
答:当,时,这两块园地一共种植了株蔬菜.
24.(1)
(2)
【分析】本题考查了整式的混合运算,代数式求值,掌握整式混合运算的法则是解题的关键.
(1)根据梯形的面积公式列出代数式,然后根据整式的混合运算法则进行计算即可;
(2)先代入求出梯形面积,再根据棱柱的体积公式列出代数式,然后根据整式的混合运算法则进行计算即可.
【详解】(1)解:河道横截面的面积为:
;
(2)当时,
,
,
答:长的南水北调的河道最多可以蓄水.
25.(1)
(2)
(3)直线垂直平分
【分析】本题考查的是轴对称的性质,理解轴对称的含义是解本题的关键;
(1)根据四边形与四边形关于直线对称,可得对应边相等,从而可得答案;
(2)先求解,再根据轴对称的性质可得答案;
(3)根据对称轴垂直平分对称点的连线,可得答案;
【详解】(1)解:∵四边形与四边形关于直线对称.,
∴;
(2)解:∵,
∴,
由轴对称的性质可得:
;
(3)解:∵对称轴垂直平分对称点的连线,
∴直线垂直平分.
26.(1)见解析
(2)平行且相等
(3)24
【分析】本题考查了平移作图以及平移的性质,熟练掌握平移的性质是解题的关键;
(1)根据平移的性质,画出该部分图形向右平移4格后的图形,即可求解;
(2)根据平移的性质即可求解;
(3)根据2个平行四边形的面积和,即可求解.
【详解】(1)解:如图所示,
(2)根据平移的性质可得:与平行且相等
故答案为:平行且相等.
(3)折线在平移过程中扫过的面积为四边形.
27.(1)
(2)
(3)秒或秒
【分析】(1)根据,求出旋转角即可;
(2)根据,利用补角性质求出,根据所在的射线恰好平分,得出,再求出旋转角即可;
(3)设三角板运动的时间为t秒,当平分时,根据的一半与旋转角相等,列方程,当平分时,根据的一半与旋转角相等,列方程,解方程即可.
【详解】(1)解:∵在射线上,三角板绕点О按顺时针方向旋转,,
旋转角,
三角板旋转的角度为,
故答案为:;
(2)解:∵,
∴,
∵所在的射线恰好平分,
∴,
∴旋转角,
故答案为:;
(3)解:设三角板运动的时间为t秒,则,,
当平分时,,如图:
,
解得;
当平分时,,如图:
,
解得;
综上可知,三角板运动的时间为秒或秒.
【点睛】本题考查旋转的性质,补角的性质,角平分线定义,图形中的角度计算,一元一次方程的应用,熟练运用分类讨论思想是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
