人教版物理高二选修2-2第一章第四节力矩的平衡条件同步练习
文档属性
| 名称 | 人教版物理高二选修2-2第一章第四节力矩的平衡条件同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 440.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-05-26 00:00:00 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
人教版物理高二选修2-2第一章
第四节力矩的平衡条件同步练习
一.选择题
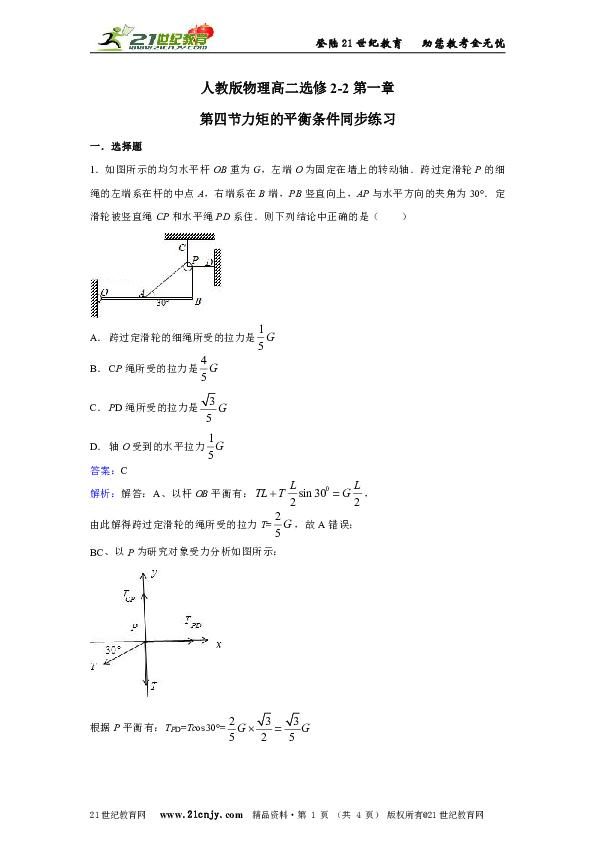
1.如图所示的均匀水平杆OB重为G,左端O为固定在墙上的转动轴.跨过定滑轮P的细绳的左端系在杆的中点A,右端系在B端,PB竖直向上,AP与水平方向的夹角为30°.定滑轮被竖直绳CP和水平绳PD系住.则下列结论中正确的是( )
A. 跨过定滑轮的细绳所受的拉力是
B. CP绳所受的拉力是
C. PD绳所受的拉力是
D. 轴O受到的水平拉力
答案:C
解析:解答:A、以杆OB平衡有:,
由此解得跨过定滑轮的绳所受的拉力T=,故A错误;
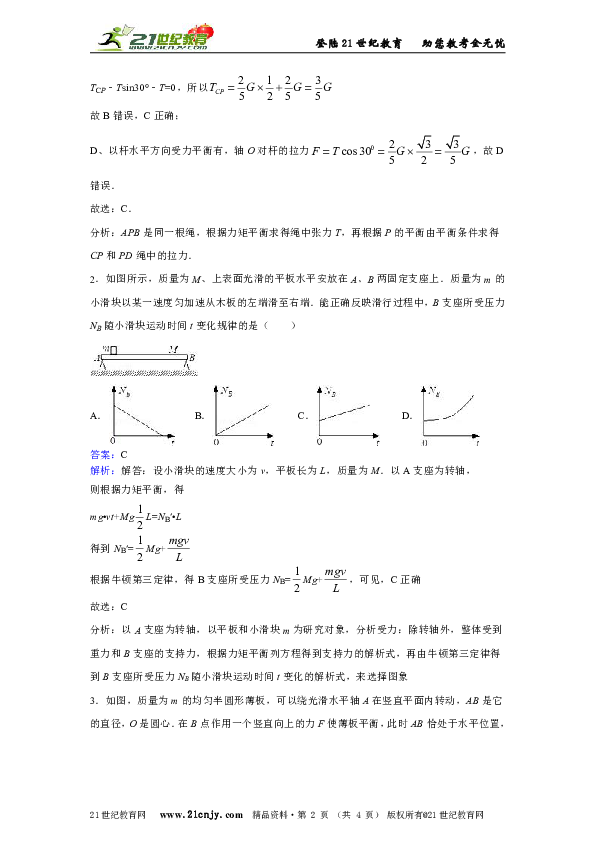
BC、以P为研究对象受力分析如图所示:
根据P平衡有:TPD=Tcos30°=
TCP﹣Tsin30°﹣T=0,所以
故B错误,C正确;
D、以杆水平方向受力平衡有,轴O对杆的拉力,故D错误.
故选:C.
分析:APB是同一根绳,根据力矩平衡求得绳中张力T,再根据P的平衡由平衡条件求得CP和PD绳中的拉力.
2.如图所示,质量为M、上表面光滑的平板水平安放在A、B两固定支座上.质量为m的小滑块以某一速度匀加速从木板的左端滑至右端.能正确反映滑行过程中,B支座所受压力NB随小滑块运动时间t变化规律的是( )
A. B. C. D.
答案:C
解析:解答:设小滑块的速度大小为v,平板长为L,质量为M.以A支座为转轴,
则根据力矩平衡,得
mg vt+MgL=NB′ L
得到NB′=Mg+
根据牛顿第三定律,得B支座所受压力NB=Mg+,可见,C正确
故选:C
分析:以A支座为转轴,以平板和小滑块m为研究对象,分析受力:除转轴外,整体受到重力和B支座的支持力,根据力矩平衡列方程得到支持力的解析式,再由牛顿第三定律得到B支座所受压力NB随小滑块运动时间t变化的解析式,来选择图象
3.如图,质量为m的均匀半圆形薄板,可以绕光滑水平轴A在竖直平面内转动,AB是它的直径,O是圆心.在B点作用一个竖直向上的力F使薄板平衡,此时AB恰处于水平位置,若保持力F始终竖直向上,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB接近竖直位置的过程中,力F对应的力矩为M,则M、F大小变化情况是( )
A. M变小,F不变 B. M、F均变大
C. M、F均先变大再变小 D. M先变大再变小,F始终变大
答案:C
解析:解答:以A点为支点,拉力F有力矩,重力也有力矩;设重力的作用点在P点,如图:
保持力F始终竖直,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB到达竖直位置的过程中,重心P与A点的水平距离先变大后变小,故重力的力矩M′先变大后变小;而拉力的力臂是逐渐变小;
设AB与竖直方向夹角为θ,根据力矩平衡条件,有:
F 2Rsinθ=M=M′
故:F=,故F先增加后减小;
故选:C.
分析:以A点为支点,拉力F有力矩,重力也有力矩,找出重心后,根据力矩平衡条件列式分析即可.
4.根据汉族民间传说,木杆秤是鲁班发明的.它是我国民间过去很长时间一直使用的称量物体质量的衡器.通常它是由一根一头粗、一头细的质量分布不均匀的直杆、称钩(BD)、提纽(O)、用可左右移动的轻线悬挂的称砣(质量为m)组成.称杆与称钩整体的重心在C点.不称物体时,将称砣置于A处,此时手提提纽,称杆恰能水平平衡.因而A点质量的刻度为零.当称钩上悬挂重物时,秤砣向右移动x到P点时重新平衡.则下列有关说法正确的是( )
A. 杆秤上的刻度一定是均匀的
B. 其它条件不变,OB之间的距离越小,称量范围越小
C. 其它条件不变,砣的质量越大,秤量范围越小
D. 如果在加速上升的电梯中,杆秤称量计数将偏大
答案:A
解析:解答:A、由图可知,OA之间的距离为a,OB之间的距离为b,OC之间的距离为c,设OB杆的质量为m0,秤砣与A之间的距离为x,当秤砣在A点到达平衡时:
m0g c=(m+m′)g a ①
当秤砣在距离A点的距离为x到达平衡时.得:
m0g c+Mg b=m′ga+mg(a+x)
联立以上二式得:M b=m x ②
即,重物 的质量与秤砣到A点的距离成正比,所以杆秤上的刻度一定是均匀的.故A正确;
B、由②式可知,,其它条件不变,OB之间的距离b越小,称量的质量的范围越大.故B错误;
C、由②式可知,,其它条件不变,砣的质量越大,秤量范围越大.故C错误;
D、若在加速上升的电梯中,设加速度大小为:a0,当秤砣在距离A点的距离为x到达平衡时.得:
m0(g+a0) c+M(g+a0) b=m′(g+a0) a+m(g+a0)(a+x)
整理得:M b=m x,可知与电梯的加速度无关.所以如果在加速上升的电梯中,杆秤称量计数不变.
故D错误.
故选:A
分析:杆秤利用杠杆的平衡条件,通过力臂的大小关系得出物体的质量与秤砣的质量之间的关系,测量物体的质量.该题根据该原理解答即可.
5.如图所示,一根绳子一端固定于竖直墙上的A点,另一端绕过动滑轮P悬挂一重物B,其中绳子的PA段处于水平状态.另一根绳子一端与动滑轮P的轴相连,在绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F,使整个系统处于平衡状态.滑轮均为光滑、轻质,且均可看作质点.现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态,则该平衡状态与原平衡状态相比较( )
A. 拉力F不变 B. 拉力F减小 C. 角θ不变 D. 角θ减小
答案:D
解析:解答:向左缓慢缓慢移动一小段距离,绳变短,动滑轮要上移,绳PA和PB间的夹角变小,而绳QP位于PA和PB间的角平分线上,所以角θ减小.
经过定滑轮的绳子拉力大小相等,等于mg,两根绳子的合力与QP绳的拉力大小相等,方向相反.因为夹角变小,合力变大,QP绳的拉力就大,所以拉力F增加.故A错误、D正确,B、C错误.
故选:D.
分析:对滑轮P受力分析,抓住三根绳子合力为零,AP、BP绳子拉力大小相等,通过角度的变化进行分析.
6.光滑直杆AB和BC按如图所示连接,A、C处与竖直墙用铰链连接,两杆在B点也用铰链连接,杆及铰链的质量与摩擦都不计.ABC构成一直角三角形,BC与墙垂直,将重力为G、可视为质点的物块P从A点静止释放,则物块从A运动到B的过程中( )
A. AB杆对BC杆的作用力方向垂直AB杆向右上方
B. C处铰链对BC杆的作用力不变
C. A处铰链对AB杆的作用力方向不变
D. A处铰链对AB杆的作用力先变小后变大
答案:D
解析:解答:A、杆的质量与摩擦不计,BC杆受到墙壁C处的作用力与AB杆的作用力,墙壁对BC的作用力水平向右,BC杆静止处于平衡状态,由平衡条件可知,AB杆对BC的作用力水平向左,故A错误;
B、以A为支点,物块P向下滑动过程中,物块P对AB的压力不变,力臂逐渐变大,力矩变大,BC对AB的作用力的力臂大小不变,由力臂平衡条件可知,BC对AB的作用力变大,由牛顿第三第定律可知,AB对BC的作用力逐渐变大,杆BC静止,处于平衡状态,由平衡条件可知,C对BC的作用力等于AB对BC的作用力,则C对BC的作用力逐渐变大,故B错误;
C、BC对AB的作用力FBC方向不变,大小逐渐增大,物块P对AB的作用力N大小与方向都不变,A处对AB的作用力FA如图所示,由图示可知,物块P下滑过程,A处对AB的作用力方向不断变化,由图示可知,FA先变小后变大,当FA与FBC垂直时FA最小,C错误,D正确;
故选:D.
分析:对BC受力分析,然后确定AB对BC的作用力方向;
以A为支点应用力矩平衡条件判断BC对AB的作用力如果变化,然后判断C处作用力的变化情况;
根据AB的受力情况应用平衡条件与力矩平衡条件分析答题.
7.如图,AB、CD分别是两个质量均为m、可以绕A、C两固定水平光滑转轴转动的匀质细杆,D为AB杆的中点,且AC=AD,现在B端施加一个始终垂直AB杆的力F 使杆处于静止状态,DC与水平面的夹角为α,g为重力加速度.则下列说法正确的是( )
A. 若CD与AB杆接触处光滑,D端受到的CD杆的作用力大小为
B. 若CD与AB杆接触处光滑,D端受到的CD杆的作用力大小为
C. 若CD与AB杆接触处有摩擦,则力F比接触处光滑时要大
D. 无论接触处是否光滑,及转动方向如何,力F均为一定值
答案:A
解析:解答:设AB杆的长度是2L,杆CD进行受力分析,画出各个力的力臂如图:
则重力的力臂: ①
CD的支持力的力臂: ②
由力矩平衡的条件得:mg L1=FN L2 ③
联立①②③得:
A、由以上分析可得,D端受到的CD杆的作用力大小为为mg.故A正确,B错误;
C、D、若C与AB杆接触处有摩擦,杆AB要分成顺时针转动与逆时针转动两种情况:
1.杆AB顺时针转动时,杆CD相对于AB向上运动,CD在D点受到的摩擦力的方向向下,摩擦力产生顺时针方向的力矩,由力矩平衡的条件得:
mg L1+Mf=FN′ L2
所以此时
2.杆AB逆时针转动时,杆CD相对于AB向下运动,CD在D点受到的摩擦力的方向向上,摩擦力产生逆时针方向的力矩,由力矩平衡的条件得:
mg L1=FN″ L2+Mf
所以:.故C错误,D错误.
故选:A
分析:设AB杆的长度是2L,然后对杆CD进行受力分析,画出各个力的力臂,然后又力矩平衡的条件即可解答.
8.如图所示,T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,若支架表面光滑,当小物体经过C点时,B端受到的弹力为N1;若支架和小物体间有摩擦,并从A端给小物体一定的初速度,小物体恰好沿AB匀速下滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )
A. N1=0 B. N1<N2 C. N1>N2 D. N1=N2
答案:B
解析:解答:设物体经过C时对支架的压力大小为N.以O为支点.
当支架和小物体间光滑,小物体经过C时,根据力矩平衡得知N1的力矩与物块对支架压力的力矩平衡,即:
MN1=MN.
当小物体匀速下滑经过C时,N2的力矩等于摩擦力的力矩和物块对支架压力的力矩的和,即MN2=Mf+MN.
由于两次物块对支架压力的力矩相等,得MN2=MN1+Mf,则有MN1<MN2,而力臂不变,所以N1<N2.
故选:B
分析:以O为支点,根据力矩平衡条件研究N1与N2的大小关系.支架和小物体间光滑,当支架和小物体间光滑小物体经过C时,N1的力矩与物块对支架压力的力矩平衡.当小物体匀速下滑经过C时,N2的力矩等于摩擦力的力矩和物块对支架压力的力矩的和.
9.如图,光滑的平台上有一质量为20kg长为10.0m质量分布均匀的木板AB,其中7.0m伸出平台,O点是其重心.为了不使木板翻倒,起初让一个质量为30kg的小孩站在长木板的右端.关于木板的平衡问题,下列说法正确的是( )
A. 若小孩从木板右端向左端走动,小孩在木板上走动的距离不能超过3.0m
B. 若小孩从木板右端向左端走动,小孩在木板上走动的距离不能超过5.0m
C. 小孩可以在木板上向左随意走动,但决不能从左端离开长木板,否则木板就会翻倒
D. 小孩不但可以在木板上向左端随意走动,而且还可以从左端离开木板,木板也不会翻倒
答案:D
解析:解答:平台光滑,说明小孩和木板组成的系统动量守恒.小孩从木板右端B向左端A走动时,木板将沿平台向右移动,二者相对于平台的动量的大小相等,即:
m人v人=m木v木.
设经过时间t小孩走到A端,则:m人人t=m木木t,
即m人s人=m木s木,
又 s人+s木=10m,
联立二式解得:s木=6m,此时,木板的重心已向右移到了平台上.
此时以桌边为支点,木板重力的力矩大小为:M板=m木g(s木﹣2)=200×(6﹣2)N m=800N m
小孩的重力力矩大小为:M人=m人g(7﹣s木)=300×(7﹣6)N m=300N m
由于M板>M人,故即使小孩从左端A离开木板,木板也不会翻倒,故ABC错误,D正确.
故选:D.
分析:由题意,平台光滑,小孩和木板组成的系统动量守恒,根据动量守恒定律分析人与板的位移关系,判断木板重心的位置,确定能否翻倒.
10.如图,竖直轻质悬线上端固定,下端与均质硬棒AB中点连接,棒长为线长的两倍.棒的A端用铰链墙上,棒处于水平状态.改变悬线的长度,使线与棒的连接点逐渐右移,并保持棒仍处于水平状态.(若一个物体受三个力而处于平衡状态,那么这三个力一定是共点力)则悬线拉力( )
A. 逐渐减小 B. 逐渐增大 C. 先减小后增大 D. 先增大后减小
答案:A
解析:解答:棒子O端用水平轴铰接在墙上,棒处于水平状态,知悬线拉力的力矩和重力力矩平衡,重力力矩不变,当改变悬线的长度,使线与棒的连接点逐渐右移,0点到悬线的垂直距离不断增大,则拉力的力臂增大,所以拉力的大小先逐渐减小.故A正确,BCD错误.
故选:A.
分析:根据力矩平衡知,拉力的力矩与重力力矩平衡,根据拉力力臂的变化判断拉力的变化.
11.如图所示,杠杆的两端分别悬挂重物G1、G2后保持水平平衡,如果用水平力F向左缓慢拉起物体G2,使悬挂物体G2的悬线向左偏离竖直方向,则( )
A. 杠杆的A端将下降 B. 杠杆的B端将下降
C. 杠杆仍保持平衡 D. 细线BC上的拉力将保持不变
答案:C
解析:解答:根据杠杆的平衡条件,动力×动力臂=阻力×阻力臂,即G1×L1=G2×L2;
当有力作用在G2上时,绳偏离竖直方向角度为α,则此时绳拉力为T,此时G2处于三力平衡状态,
拉力F与绳的拉力T的合力等于G2的重力,即T×Lcosa=Tcosa×L2=G2×L2
即当有力时左边力矩不变,故杠杆仍处于平衡.
故选:C
分析:(1)根据杠杆的平衡条件,动力×动力臂=阻力×阻力臂,即G1×L1=G2×L2;
(2)当有力F作用在G2上时,设绳偏离竖直方向角度为α,则此时绳拉力为T,表示此时力矩T×Lcosa根据力的正交分解和数学关系判定是否平衡.
12.如图,T字形架子ABO可绕通过O点,且垂直于纸面的转动轴自由转动.现在其A端与B端分别施以图示方向的力F1和F2,则关于F1和F2产生的力矩M1和M2,下列说法正确的是( )
A. M1引起T形架顺时针转动,M2引起T形架逆时针转动
B. M1和M2可能使T形架保持平衡
C. M1和M2使T形架逆时针转动
D. M1和M2使T形架顺时针转动
答案:C
解析:解答:根据图示由右手定则可知,力F1的力矩M1使T形架沿逆时针方向转动,力F2的力矩M2也使T形架沿逆时针方向转动,所以M1和M2使T形架逆时针转动;故C正确,ABD错误;
故选:C.
分析:物体在力矩作用下会绕转动轴转动,物体沿力矩方向转动,力矩方向可以用右手定则判断,右手四指指向力臂的方向,四指向力的方向弯曲,则大拇指所指的方向就是力矩的方向,即物体的转动方向.
13.如图,一根木棒AB在O点被悬挂起来,在A、C两点分别挂两个和三个钩码,AO=OC,木棒处于平衡状态.如在A点再挂两个钩码的同时,在C点再挂三个钩码,则木棒( )
A. 绕O点顺时针方向转动
B. 绕O点逆时针方向转动
C. 平衡可能被破坏,转动方向不定
D. 仍能保持平衡状态
答案:A
解析:解答:以O为转动轴,设AO=OC=L,木棒的重力力矩为M,每个钩码的重力为G.
木棒原来处于平衡状态,根据力矩平衡条件得:2GL+M=3GL;
可得 M=GL
当在A点再挂两个钩码的同时,在C点再挂三个钩码,顺时针力矩之和为:
M顺=6GL
逆时针力矩之和为:M逆=4GL+M=5GL<M顺,所以木棒将绕O点顺时针方向转动,故A正确.
故选:A.
分析:原来木棒处于平衡状态,力矩平衡,根据力矩平衡条件可求得木棒的重力对O点的力矩;再分析在A点和C点增加砝码后,顺时针力矩和逆时针力矩的大小关系,即可判断木棒的状态.
14.如图所示,粗糙斜面上有一绕有线圈的滚筒A,线圈中通有电流,空间有一竖直方向的匀强磁场.在下列四种情况中由静止释放滚筒,滚筒可能保持静止状态的是( )
A. B. C. D.
答案:C
解析:解答:由图,滚筒与斜面的接触点为支点,滚筒受到重力、支持力、摩擦力和安培力的作用,其中支持力和摩擦力过支点,重力的力矩是逆时针的,安培力的力矩必须为顺时针才可能使滚筒保持平衡.
A、线框所受安培力左边向左,右边向右,力臂相等,安培力的合力矩是为零的,所以滚筒不能平衡,故A错;
B、线框所受安培力左边向右,右边向左,力臂相等,合力矩为零,所以滚筒不能平衡,故B错;
C、左边安培力水平向左,右边安培力水平向右,大小相等,但是力臂不等,合力矩为顺时针方向,所以滚筒可能平衡,故C正确;
D、安培力方向与C中相反,大小相等,但是力臂不等,合力矩为逆时针方向,所以滚筒不可能平衡,故D错误.
故选:C.
分析:滚筒与斜面的接触点为支点,滚筒受到重力、支持力、摩擦力和安培力的作用,其中支持力和摩擦力过支点,重力的力矩是逆时针的,安培力的力矩必须为顺时针才可能使滚筒保持平衡.然后根据力矩平衡的条件逐项分析即可.
15.关于力矩,下列说法中正确的是( )
A. 力对物体的转动作用效果决定于力矩的大小和方向
B. 力不等于零时,力对物体一定产生转动作用
C. 力矩等于零时,力对物体也可以产生转动作用
D. 力矩的单位是“牛 米”,也可以写成“焦”
答案:A
解析:解答:A、力矩是矢量,其大小不仅决定于力的大小,同时与矩心的位置有关,力矩的大小和方向决定着力对物体的转动作用,故A正确;
BC、当力的大小为零或力臂为零时,则力矩为零,此时力对物体没有产生转动的作用;故BC错误;
D、力矩的单位是N m或kN m,焦耳是力与位移的乘积,而力矩中的米是距离,不是位移,故D错误.
故选:A
分析:作用力使物体绕着转动轴或支点转动的趋向,称为力矩.力矩能够使物体改变其旋转运动.
二.填空题
16.如图所示,一根不均匀的铁棒AB与一辆拖车相连接,连接端B为一固定水平转动轴,拖车在水平面上做匀速直线运动,棒长为L,棒的质量为40kg,它与地面间的动摩擦因数为,棒的重心C距转动轴为,棒与水平面成30°角.运动过程中地面对铁棒的支持力为 N;若将铁棒B端的固定转动轴向下移一些,其他条件不变,则运动过程中地面对铁棒的支持力将比原来 (选填“增大”、“不变”或“减小”).
答案:200|增大
解析:解答:以B点为转轴,在拖车在水平面上向右做匀速直线运动过程中,棒的力矩平衡,设棒与水平面的夹角为α.则有mgcosα=NLcosα+fLsinα ①
又滑动摩擦力f=μN.
联立得:2mgcosα=3Ncosα+3μNsinα ②
解得,
α=30°代入解得,N=200N
若将铁棒B端的固定转动轴向下移一些,α减小,tanα减小,由③得知,N增大.
故答案为:200,增大.
分析:选取接端B为转动轴,地面对铁棒的支持力的力矩与重力的力矩平衡,写出平衡方程,即可求出地面对铁棒的支持力;若将铁棒B端的固定转动轴向下移一些则AB与地,地面之间的夹角减小,同样,可以根据力矩平衡的公式,判定地面对铁棒的支持力的变化.
17.如图,重为G的物体,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上.转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆AB和BC的质量不计,A、B、C三处均用铰链连接.当物体处于平衡状态时,杆AB所受力的大小为 ,杆BC所受力的大小为 .
答案:2.73G|3.73G
解析:解答:以A为支点,AB受到BC的支持力和两个绳子的拉力,它们的力臂如图1,设AB杆的长度为L,则:
竖直向下的拉力的力臂;L1=L
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL1+GL2=FBC L3
代入数据得:FBC=3.73G
同理,以C为支点,BC受到AB的拉力和两个绳子的拉力,它们的力臂如图2,则:
竖直向下的拉力的力臂:;
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL4+GL5=FAB L6
代入数据得:FAB=2.73G
故答案为:2.73G;3.73G
分析:画出各个力,分别作出各个力的力臂,然后又力矩的平衡即可解答.
18.重为G的均匀直杆AB一端用铰链与墙相连,另一端用一条通过光滑的小定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=AB.滑轮与绳重力不计.则B点处绳子的拉力的大小是 N,轴对定滑轮M的作用力大小是 N.
答案:|
解析:解答:杆处于力矩平衡状态,设绳子的拉力为F,杆长为L,则由力矩平衡条件可知:
G=F +F;
解得:F=;
滑轮受两绳的拉力及轴对定滑轮的作用力而处于平衡,即轴对定滑轮的作用力与两边绳子的拉力相等,则由力的平行四边形可求得两拉力的合力即为定滑轮对轴的作用力:
由几何关系可知:
而轴对定滑轮的作用力与F'大小相等,方向相反;
故答案为:;
分析:由受力分析可知,杆受B点绳子的拉力、C点绳子的拉力及本身的重力作用处于转动平衡状态;由力矩平衡条件可求得绳子的拉力;由力的合成可求得轴对定滑轮的作用力.
19.如图所示,为一水阀的示意图,C为轻活塞,截面积为10cm2,AB是长为0.8m的轻质杠杆,O为转轴,AO的长度为0.2m,各接触处均光滑.已知大气压强为1.0×105Pa,自来水管内的压强为2.5×105Pa.为保持AB杆水平而水不流出,则在B端需挂一质量为 kg的重物,此时转轴对杆的作用力大小为 N.
答案:5|200
解析:解答:根据力矩平衡知(PS﹣P0S) AO=mg OB
则
对O受力分析知转轴对杆的作用力大小
F=mg+(P﹣P0)S=50N+(2.5﹣1)×105×10×10﹣4N=200N
故答案为:5 200
分析:根据力矩平衡知(PS﹣P0S) AO=mg OB求解质量m,根据力与平衡求解转轴对杆的作用力.
20.半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,质点处在水平轴O的正下方位置.现以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度时,质点m的速度最大,则恒力F= ;若圆盘转过的最大角度则此时恒力F= .
答案:mg|
解析:解答:以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度时,质点m的速度最大,此时力矩平衡,故:
F r=mg 2rsin30°
解得:F=mg;
根据能量守恒定律得
解得
本题答案是:mg,.
分析:两圆盘转过的角度θ时,两个物体构成的系统减小的重力势能等于增加的动能,根据机械能守恒定律列式求解;当F的力矩大于mg的力矩时,质点m的速度增大,当F的力矩小于mg的力矩时,质点m的速度减小,则当两者力矩相等时,质点m的速度最大.根据力矩平衡条件列方程求解.再能量守恒定律求解F.
21.可轻杆OA绕转轴O自由转动,用轻绳AB和轻弹簧BC连接,位置如图所示.将质量m的小物块悬挂在轻杆中点处,静止后OA处在水平位置,轻绳AB伸直但无拉力,则此时弹簧上的弹力大小为 ;将m右移OA/4的距离,轻绳上拉力大小为 .
答案:|
解析:解答:设OA长为l,当绳无拉力,则弹簧的拉力的力矩与重力的力矩平衡,即:Flocsin60°=mg;
当m右移的距离时,由力矩平衡得:Flocsin60°+Tlsin30°=mg;
解得:
答案为:
分析:杠杆平衡的条件:动力乘以动力臂等于阻力乘以阻力臂;如图所示,根据直角三角形角与边的关系,求出绳子对杠杆拉力的力臂;再利用已知的重力和重力的力臂以及杠杆平衡的条件求出拉力F的大小.
三.解答题
22.改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm.
(1)(多选题)做这样改进的优点是( )
A.力传感器既可测拉力又可测压力
B.力传感器测力时不受主观判断影响,精度较高
C.能消除转轴摩擦引起的实验误差
D.保证力传感器所受拉力方向不变
答案:BF
(2)某同学用该装置做实验,检验时发现盘停止转动时G点始终在最低处,他仍用该盘做实验.在对力传感器进行调零后,用力传感器将力矩盘的G点拉到图示位置,此时力传感器读数为3N.再对力传感器进行调零,然后悬挂钩码进行实验.此方法 (选填“能”、“不能”)消除力矩盘偏心引起的实验误差.已知每个钩码所受重力为1N,力矩盘按图示方式悬挂钩码后,力矩盘所受顺时针方向的合力矩为 N m.力传感器的读数为 N.
答案:能|0.7|﹣0.5
解析:解答:(1)A、弹簧可以测拉力和压力,故A错误;
B、力传感器,定滑轮固定在横杆上,替代原装置中的弹簧秤,主要好处是:力传感器测力时,不受主观判断影响,精确度高和保证力传感器所受拉力方向不变,故BD正确;
C、不能消除转轴摩擦力引起的误差,故C错误;
故选:BD.(2)某同学该装置做实验,检验时发现盘停止转动时,他仍用该盘做实验,在对力传感器进行调零后,用力传感器将力矩盘的G点拉到图示位置,此时力传感器读数为3N,说明此时偏心的顺时针力矩M0=3×2×0.05N m=0.3N m;
再对力传感器进行调零,这时就可以消除力矩盘的偏心引起实验误差,力矩盘所受顺时针方向合力矩M1=2×1×0.05﹣2×1×3×0.05﹣0.3N m=0.7N m;
根据固定转动轴物体平衡条件,则有:
F×2×0.05+3×1×3×0.05﹣0.3=2×1×0.05﹣2×2×3×0.05﹣0.3;
解得:F=﹣0.5N;
故答案为:(1)BF;(2)能,0.7,﹣0.5.
分析:(1)根据弹簧可以拉伸与压缩,结合实验原理,及操作步骤,即可求解;(2)根据力矩公式,结合力传感器读数,求得偏心的顺时针力矩,再消除力矩盘的偏心引起实验误差,求得力矩盘所受顺时针方向合力矩,从而根据平衡条件,即可求解.
23.用如图所示装置做“研究有固定转动轴物体平衡条件“的实验,力矩盘上个同心圆的间距相等.
(1)(多选)在用细线悬挂钩码前,以下哪些措施是必要的
A.判断力矩盘是否在竖直平面 B.判断横杆MN是否严格保持水平
C.判断力矩盘与转轴间的摩擦是否足够小 D.判断力矩盘的重心是否位于盘中心
答案:ACD
(2)在A、B、C三点分别用细线悬挂钩码后,力矩盘平衡,如图所示,已知每个钩码所受的重力为1牛,则此时弹簧称示数为 牛.
答案:4
(3)由于力矩盘偏心未经调整实际测出的弹簧称读数偏大,则力矩盘的重心在轴的 .(填左方或右方)
答案:右方
解析:解答:(1)A、为了防止细线及弹簧称与力矩盘摩擦,判断力矩盘是否处在竖直平面是必要的.故A正确.
B、本实验与横杆MN是否平衡无关,没有必要检查横杆MN是否严格保持水平.故B错误.
C、D、本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系,重力、摩擦力等影响要尽可能小,故CD正确.
故选:ACD.(2)设A、B、C三处拉力大小分别为FA、FB、FC,弹簧称示数为F,由题
FA=1N,FB=1N,FC=3N
设力矩盘上相邻同心圆间距为r,则弹簧称拉力的力臂为L=2r
根据力矩平衡得:
FA 2r+FL=FB r+FC 3r
代入解得:F=4N;(3)由于力矩盘偏心未经调整实际测出的弹簧称读数偏大,因此力矩盘重心在轴的右方,才会导致弹簧秤实际读数偏大,
故答案为:(1)ACD(2)4;(3)右方.
分析:(1)本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系,要尽可能减小其他力的影响,比如重力、摩擦力等影响.根据此要求分析选择.(2)分别确定A、B、C三点细线拉力大小和力臂大小,根据力矩平衡求出弹簧称拉力;(3)根据力矩盘心在轴的某一方,结合力矩平衡条件,即可得出弹簧称实际读数偏大还是偏小.
24.在研究有固定转动轴物体平衡条件的实验中
(1)实验开始前需要检查力矩盘重心是否在转轴处,描述检查的操作过程.
答案:心在转轴上,力矩盘本身的重力才可以忽略不计,转动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上
(2)某同学采用50g的钩码,力矩盘平衡后如图所示,弹簧秤读数1.1N,盘面中3个同心圆半径分别是2cm、4cm、6cm.填写下表(g取9.8m/s2,答案精确到0.001N m):
顺时针力矩 逆时针力矩
0.059N m
答案: 0.064N m
解析:解答:(1)心在转轴上,力矩盘本身的重力才可以忽略不计,转动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上;(2)逆时针力矩为M=1.1×4×10﹣2+50×10﹣3×10×4×10﹣2=0.064N m.
故答案为:(1)在任意位置(转过任意角度)能静止/平衡.(2)0.064N m
分析:(1)动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上;(2)簧秤读数1.1N,一个钩码重50g,根据力矩等于力与力臂的乘积.
25.如图所示是一个半径为R的轮子,它绕固定转动轴O顺时针方向转动,两侧各有一个长为L的竖直杆MO和NQ,它们都固定在天花板上M、N处(如图所示).两轻杆上距轴为a处各固定一宽度为b的摩擦块(上下厚度不计).摩擦块与轮子间动摩擦因数都是μ(μ<),不计杆与摩擦块的重力.为使轮子刹停,在两杆下端P、Q之间用轻绳悬挂一重物.刚好使三根细绳之间夹角都相等.
(1)有同学认为:“由于该装置高度对称,所以两边摩擦力的大小是相等的”.你认为这位同学的看法是否正确?为什么(请简要说明你的理由)?
答案:这位同学的看法是不正确,因为受力(或力矩)情况并不对称;
(2)设AP和AQ上的拉力的大小都是F,则左、右两侧摩擦力作功之比是多少?
答案:设AP和AQ上的拉力的大小都是F,则左、右两侧摩擦力作功之比是;
(3)为使轮子在规定的时间内能停下,规定制动力矩的大小为M.求此时在下方悬挂物体的重力G是多大?
答案:为使轮子在规定的时间内能停下,规定制动力矩的大小为M.此时在下方悬挂物体的重力G是
解析:解答:(1)这位同学的看法是不正确,因为受力(或力矩)情况并不对称. (2)对左侧的杆进行受力分析如图,摩擦力与拉力产生逆时针方向的力矩,支持力N1产生顺时针方向的力矩,根据力矩平衡得:μN1b+Fcos30°L=N1a
代入数据解得:
同理对右侧的杆进行受力分析如图,摩擦力与拉力产生顺时针方向的力矩,支持力N1产生逆时针方向的力矩,根据力矩平衡得:μN2b+N2a=FLcos30°
代入数据得:
轮子停下的过程中,两侧的路程相同,根据W=FS
所以:(3)由题图可知,轮子制动的过程中,受到的两侧的摩擦力的方向都与轮子边缘的质点运动的方向相反,所以轮子制动的力矩的方向与轮子转动的方向相反,制动的力矩大小:
联立解得:
分析:(1)(2)分别对左右两侧的杆进行受力分析,结合力矩平衡即可求出左右两侧受到的摩擦力,从而判断出两侧的摩擦力是否相等;再结合功的计算公式即可求出左、右两侧摩擦力作功之比.(3)对轮子进行受力分析,求出轮子受到的摩擦力的力矩的表达式,然后结合(2)中的摩擦力的表达式即可求出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 22 页 (共 23 页) 版权所有@21世纪教育网
人教版物理高二选修2-2第一章
第四节力矩的平衡条件同步练习
一.选择题
1.如图所示的均匀水平杆OB重为G,左端O为固定在墙上的转动轴.跨过定滑轮P的细绳的左端系在杆的中点A,右端系在B端,PB竖直向上,AP与水平方向的夹角为30°.定滑轮被竖直绳CP和水平绳PD系住.则下列结论中正确的是( )
A. 跨过定滑轮的细绳所受的拉力是
B. CP绳所受的拉力是
C. PD绳所受的拉力是
D. 轴O受到的水平拉力
答案:C
解析:解答:A、以杆OB平衡有:,
由此解得跨过定滑轮的绳所受的拉力T=,故A错误;
BC、以P为研究对象受力分析如图所示:
根据P平衡有:TPD=Tcos30°=
TCP﹣Tsin30°﹣T=0,所以
故B错误,C正确;
D、以杆水平方向受力平衡有,轴O对杆的拉力,故D错误.
故选:C.
分析:APB是同一根绳,根据力矩平衡求得绳中张力T,再根据P的平衡由平衡条件求得CP和PD绳中的拉力.
2.如图所示,质量为M、上表面光滑的平板水平安放在A、B两固定支座上.质量为m的小滑块以某一速度匀加速从木板的左端滑至右端.能正确反映滑行过程中,B支座所受压力NB随小滑块运动时间t变化规律的是( )
A. B. C. D.
答案:C
解析:解答:设小滑块的速度大小为v,平板长为L,质量为M.以A支座为转轴,
则根据力矩平衡,得
mg vt+MgL=NB′ L
得到NB′=Mg+
根据牛顿第三定律,得B支座所受压力NB=Mg+,可见,C正确
故选:C
分析:以A支座为转轴,以平板和小滑块m为研究对象,分析受力:除转轴外,整体受到重力和B支座的支持力,根据力矩平衡列方程得到支持力的解析式,再由牛顿第三定律得到B支座所受压力NB随小滑块运动时间t变化的解析式,来选择图象
3.如图,质量为m的均匀半圆形薄板,可以绕光滑水平轴A在竖直平面内转动,AB是它的直径,O是圆心.在B点作用一个竖直向上的力F使薄板平衡,此时AB恰处于水平位置,若保持力F始终竖直向上,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB接近竖直位置的过程中,力F对应的力矩为M,则M、F大小变化情况是( )
A. M变小,F不变 B. M、F均变大
C. M、F均先变大再变小 D. M先变大再变小,F始终变大
答案:C
解析:解答:以A点为支点,拉力F有力矩,重力也有力矩;设重力的作用点在P点,如图:
保持力F始终竖直,在F作用下使薄板绕A点沿逆时针方向缓慢转动,直到AB到达竖直位置的过程中,重心P与A点的水平距离先变大后变小,故重力的力矩M′先变大后变小;而拉力的力臂是逐渐变小;
设AB与竖直方向夹角为θ,根据力矩平衡条件,有:
F 2Rsinθ=M=M′
故:F=,故F先增加后减小;
故选:C.
分析:以A点为支点,拉力F有力矩,重力也有力矩,找出重心后,根据力矩平衡条件列式分析即可.
4.根据汉族民间传说,木杆秤是鲁班发明的.它是我国民间过去很长时间一直使用的称量物体质量的衡器.通常它是由一根一头粗、一头细的质量分布不均匀的直杆、称钩(BD)、提纽(O)、用可左右移动的轻线悬挂的称砣(质量为m)组成.称杆与称钩整体的重心在C点.不称物体时,将称砣置于A处,此时手提提纽,称杆恰能水平平衡.因而A点质量的刻度为零.当称钩上悬挂重物时,秤砣向右移动x到P点时重新平衡.则下列有关说法正确的是( )
A. 杆秤上的刻度一定是均匀的
B. 其它条件不变,OB之间的距离越小,称量范围越小
C. 其它条件不变,砣的质量越大,秤量范围越小
D. 如果在加速上升的电梯中,杆秤称量计数将偏大
答案:A
解析:解答:A、由图可知,OA之间的距离为a,OB之间的距离为b,OC之间的距离为c,设OB杆的质量为m0,秤砣与A之间的距离为x,当秤砣在A点到达平衡时:
m0g c=(m+m′)g a ①
当秤砣在距离A点的距离为x到达平衡时.得:
m0g c+Mg b=m′ga+mg(a+x)
联立以上二式得:M b=m x ②
即,重物 的质量与秤砣到A点的距离成正比,所以杆秤上的刻度一定是均匀的.故A正确;
B、由②式可知,,其它条件不变,OB之间的距离b越小,称量的质量的范围越大.故B错误;
C、由②式可知,,其它条件不变,砣的质量越大,秤量范围越大.故C错误;
D、若在加速上升的电梯中,设加速度大小为:a0,当秤砣在距离A点的距离为x到达平衡时.得:
m0(g+a0) c+M(g+a0) b=m′(g+a0) a+m(g+a0)(a+x)
整理得:M b=m x,可知与电梯的加速度无关.所以如果在加速上升的电梯中,杆秤称量计数不变.
故D错误.
故选:A
分析:杆秤利用杠杆的平衡条件,通过力臂的大小关系得出物体的质量与秤砣的质量之间的关系,测量物体的质量.该题根据该原理解答即可.
5.如图所示,一根绳子一端固定于竖直墙上的A点,另一端绕过动滑轮P悬挂一重物B,其中绳子的PA段处于水平状态.另一根绳子一端与动滑轮P的轴相连,在绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F,使整个系统处于平衡状态.滑轮均为光滑、轻质,且均可看作质点.现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态,则该平衡状态与原平衡状态相比较( )
A. 拉力F不变 B. 拉力F减小 C. 角θ不变 D. 角θ减小
答案:D
解析:解答:向左缓慢缓慢移动一小段距离,绳变短,动滑轮要上移,绳PA和PB间的夹角变小,而绳QP位于PA和PB间的角平分线上,所以角θ减小.
经过定滑轮的绳子拉力大小相等,等于mg,两根绳子的合力与QP绳的拉力大小相等,方向相反.因为夹角变小,合力变大,QP绳的拉力就大,所以拉力F增加.故A错误、D正确,B、C错误.
故选:D.
分析:对滑轮P受力分析,抓住三根绳子合力为零,AP、BP绳子拉力大小相等,通过角度的变化进行分析.
6.光滑直杆AB和BC按如图所示连接,A、C处与竖直墙用铰链连接,两杆在B点也用铰链连接,杆及铰链的质量与摩擦都不计.ABC构成一直角三角形,BC与墙垂直,将重力为G、可视为质点的物块P从A点静止释放,则物块从A运动到B的过程中( )
A. AB杆对BC杆的作用力方向垂直AB杆向右上方
B. C处铰链对BC杆的作用力不变
C. A处铰链对AB杆的作用力方向不变
D. A处铰链对AB杆的作用力先变小后变大
答案:D
解析:解答:A、杆的质量与摩擦不计,BC杆受到墙壁C处的作用力与AB杆的作用力,墙壁对BC的作用力水平向右,BC杆静止处于平衡状态,由平衡条件可知,AB杆对BC的作用力水平向左,故A错误;
B、以A为支点,物块P向下滑动过程中,物块P对AB的压力不变,力臂逐渐变大,力矩变大,BC对AB的作用力的力臂大小不变,由力臂平衡条件可知,BC对AB的作用力变大,由牛顿第三第定律可知,AB对BC的作用力逐渐变大,杆BC静止,处于平衡状态,由平衡条件可知,C对BC的作用力等于AB对BC的作用力,则C对BC的作用力逐渐变大,故B错误;
C、BC对AB的作用力FBC方向不变,大小逐渐增大,物块P对AB的作用力N大小与方向都不变,A处对AB的作用力FA如图所示,由图示可知,物块P下滑过程,A处对AB的作用力方向不断变化,由图示可知,FA先变小后变大,当FA与FBC垂直时FA最小,C错误,D正确;
故选:D.
分析:对BC受力分析,然后确定AB对BC的作用力方向;
以A为支点应用力矩平衡条件判断BC对AB的作用力如果变化,然后判断C处作用力的变化情况;
根据AB的受力情况应用平衡条件与力矩平衡条件分析答题.
7.如图,AB、CD分别是两个质量均为m、可以绕A、C两固定水平光滑转轴转动的匀质细杆,D为AB杆的中点,且AC=AD,现在B端施加一个始终垂直AB杆的力F 使杆处于静止状态,DC与水平面的夹角为α,g为重力加速度.则下列说法正确的是( )
A. 若CD与AB杆接触处光滑,D端受到的CD杆的作用力大小为
B. 若CD与AB杆接触处光滑,D端受到的CD杆的作用力大小为
C. 若CD与AB杆接触处有摩擦,则力F比接触处光滑时要大
D. 无论接触处是否光滑,及转动方向如何,力F均为一定值
答案:A
解析:解答:设AB杆的长度是2L,杆CD进行受力分析,画出各个力的力臂如图:
则重力的力臂: ①
CD的支持力的力臂: ②
由力矩平衡的条件得:mg L1=FN L2 ③
联立①②③得:
A、由以上分析可得,D端受到的CD杆的作用力大小为为mg.故A正确,B错误;
C、D、若C与AB杆接触处有摩擦,杆AB要分成顺时针转动与逆时针转动两种情况:
1.杆AB顺时针转动时,杆CD相对于AB向上运动,CD在D点受到的摩擦力的方向向下,摩擦力产生顺时针方向的力矩,由力矩平衡的条件得:
mg L1+Mf=FN′ L2
所以此时
2.杆AB逆时针转动时,杆CD相对于AB向下运动,CD在D点受到的摩擦力的方向向上,摩擦力产生逆时针方向的力矩,由力矩平衡的条件得:
mg L1=FN″ L2+Mf
所以:.故C错误,D错误.
故选:A
分析:设AB杆的长度是2L,然后对杆CD进行受力分析,画出各个力的力臂,然后又力矩平衡的条件即可解答.
8.如图所示,T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,若支架表面光滑,当小物体经过C点时,B端受到的弹力为N1;若支架和小物体间有摩擦,并从A端给小物体一定的初速度,小物体恰好沿AB匀速下滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )
A. N1=0 B. N1<N2 C. N1>N2 D. N1=N2
答案:B
解析:解答:设物体经过C时对支架的压力大小为N.以O为支点.
当支架和小物体间光滑,小物体经过C时,根据力矩平衡得知N1的力矩与物块对支架压力的力矩平衡,即:
MN1=MN.
当小物体匀速下滑经过C时,N2的力矩等于摩擦力的力矩和物块对支架压力的力矩的和,即MN2=Mf+MN.
由于两次物块对支架压力的力矩相等,得MN2=MN1+Mf,则有MN1<MN2,而力臂不变,所以N1<N2.
故选:B
分析:以O为支点,根据力矩平衡条件研究N1与N2的大小关系.支架和小物体间光滑,当支架和小物体间光滑小物体经过C时,N1的力矩与物块对支架压力的力矩平衡.当小物体匀速下滑经过C时,N2的力矩等于摩擦力的力矩和物块对支架压力的力矩的和.
9.如图,光滑的平台上有一质量为20kg长为10.0m质量分布均匀的木板AB,其中7.0m伸出平台,O点是其重心.为了不使木板翻倒,起初让一个质量为30kg的小孩站在长木板的右端.关于木板的平衡问题,下列说法正确的是( )
A. 若小孩从木板右端向左端走动,小孩在木板上走动的距离不能超过3.0m
B. 若小孩从木板右端向左端走动,小孩在木板上走动的距离不能超过5.0m
C. 小孩可以在木板上向左随意走动,但决不能从左端离开长木板,否则木板就会翻倒
D. 小孩不但可以在木板上向左端随意走动,而且还可以从左端离开木板,木板也不会翻倒
答案:D
解析:解答:平台光滑,说明小孩和木板组成的系统动量守恒.小孩从木板右端B向左端A走动时,木板将沿平台向右移动,二者相对于平台的动量的大小相等,即:
m人v人=m木v木.
设经过时间t小孩走到A端,则:m人人t=m木木t,
即m人s人=m木s木,
又 s人+s木=10m,
联立二式解得:s木=6m,此时,木板的重心已向右移到了平台上.
此时以桌边为支点,木板重力的力矩大小为:M板=m木g(s木﹣2)=200×(6﹣2)N m=800N m
小孩的重力力矩大小为:M人=m人g(7﹣s木)=300×(7﹣6)N m=300N m
由于M板>M人,故即使小孩从左端A离开木板,木板也不会翻倒,故ABC错误,D正确.
故选:D.
分析:由题意,平台光滑,小孩和木板组成的系统动量守恒,根据动量守恒定律分析人与板的位移关系,判断木板重心的位置,确定能否翻倒.
10.如图,竖直轻质悬线上端固定,下端与均质硬棒AB中点连接,棒长为线长的两倍.棒的A端用铰链墙上,棒处于水平状态.改变悬线的长度,使线与棒的连接点逐渐右移,并保持棒仍处于水平状态.(若一个物体受三个力而处于平衡状态,那么这三个力一定是共点力)则悬线拉力( )
A. 逐渐减小 B. 逐渐增大 C. 先减小后增大 D. 先增大后减小
答案:A
解析:解答:棒子O端用水平轴铰接在墙上,棒处于水平状态,知悬线拉力的力矩和重力力矩平衡,重力力矩不变,当改变悬线的长度,使线与棒的连接点逐渐右移,0点到悬线的垂直距离不断增大,则拉力的力臂增大,所以拉力的大小先逐渐减小.故A正确,BCD错误.
故选:A.
分析:根据力矩平衡知,拉力的力矩与重力力矩平衡,根据拉力力臂的变化判断拉力的变化.
11.如图所示,杠杆的两端分别悬挂重物G1、G2后保持水平平衡,如果用水平力F向左缓慢拉起物体G2,使悬挂物体G2的悬线向左偏离竖直方向,则( )
A. 杠杆的A端将下降 B. 杠杆的B端将下降
C. 杠杆仍保持平衡 D. 细线BC上的拉力将保持不变
答案:C
解析:解答:根据杠杆的平衡条件,动力×动力臂=阻力×阻力臂,即G1×L1=G2×L2;
当有力作用在G2上时,绳偏离竖直方向角度为α,则此时绳拉力为T,此时G2处于三力平衡状态,
拉力F与绳的拉力T的合力等于G2的重力,即T×Lcosa=Tcosa×L2=G2×L2
即当有力时左边力矩不变,故杠杆仍处于平衡.
故选:C
分析:(1)根据杠杆的平衡条件,动力×动力臂=阻力×阻力臂,即G1×L1=G2×L2;
(2)当有力F作用在G2上时,设绳偏离竖直方向角度为α,则此时绳拉力为T,表示此时力矩T×Lcosa根据力的正交分解和数学关系判定是否平衡.
12.如图,T字形架子ABO可绕通过O点,且垂直于纸面的转动轴自由转动.现在其A端与B端分别施以图示方向的力F1和F2,则关于F1和F2产生的力矩M1和M2,下列说法正确的是( )
A. M1引起T形架顺时针转动,M2引起T形架逆时针转动
B. M1和M2可能使T形架保持平衡
C. M1和M2使T形架逆时针转动
D. M1和M2使T形架顺时针转动
答案:C
解析:解答:根据图示由右手定则可知,力F1的力矩M1使T形架沿逆时针方向转动,力F2的力矩M2也使T形架沿逆时针方向转动,所以M1和M2使T形架逆时针转动;故C正确,ABD错误;
故选:C.
分析:物体在力矩作用下会绕转动轴转动,物体沿力矩方向转动,力矩方向可以用右手定则判断,右手四指指向力臂的方向,四指向力的方向弯曲,则大拇指所指的方向就是力矩的方向,即物体的转动方向.
13.如图,一根木棒AB在O点被悬挂起来,在A、C两点分别挂两个和三个钩码,AO=OC,木棒处于平衡状态.如在A点再挂两个钩码的同时,在C点再挂三个钩码,则木棒( )
A. 绕O点顺时针方向转动
B. 绕O点逆时针方向转动
C. 平衡可能被破坏,转动方向不定
D. 仍能保持平衡状态
答案:A
解析:解答:以O为转动轴,设AO=OC=L,木棒的重力力矩为M,每个钩码的重力为G.
木棒原来处于平衡状态,根据力矩平衡条件得:2GL+M=3GL;
可得 M=GL
当在A点再挂两个钩码的同时,在C点再挂三个钩码,顺时针力矩之和为:
M顺=6GL
逆时针力矩之和为:M逆=4GL+M=5GL<M顺,所以木棒将绕O点顺时针方向转动,故A正确.
故选:A.
分析:原来木棒处于平衡状态,力矩平衡,根据力矩平衡条件可求得木棒的重力对O点的力矩;再分析在A点和C点增加砝码后,顺时针力矩和逆时针力矩的大小关系,即可判断木棒的状态.
14.如图所示,粗糙斜面上有一绕有线圈的滚筒A,线圈中通有电流,空间有一竖直方向的匀强磁场.在下列四种情况中由静止释放滚筒,滚筒可能保持静止状态的是( )
A. B. C. D.
答案:C
解析:解答:由图,滚筒与斜面的接触点为支点,滚筒受到重力、支持力、摩擦力和安培力的作用,其中支持力和摩擦力过支点,重力的力矩是逆时针的,安培力的力矩必须为顺时针才可能使滚筒保持平衡.
A、线框所受安培力左边向左,右边向右,力臂相等,安培力的合力矩是为零的,所以滚筒不能平衡,故A错;
B、线框所受安培力左边向右,右边向左,力臂相等,合力矩为零,所以滚筒不能平衡,故B错;
C、左边安培力水平向左,右边安培力水平向右,大小相等,但是力臂不等,合力矩为顺时针方向,所以滚筒可能平衡,故C正确;
D、安培力方向与C中相反,大小相等,但是力臂不等,合力矩为逆时针方向,所以滚筒不可能平衡,故D错误.
故选:C.
分析:滚筒与斜面的接触点为支点,滚筒受到重力、支持力、摩擦力和安培力的作用,其中支持力和摩擦力过支点,重力的力矩是逆时针的,安培力的力矩必须为顺时针才可能使滚筒保持平衡.然后根据力矩平衡的条件逐项分析即可.
15.关于力矩,下列说法中正确的是( )
A. 力对物体的转动作用效果决定于力矩的大小和方向
B. 力不等于零时,力对物体一定产生转动作用
C. 力矩等于零时,力对物体也可以产生转动作用
D. 力矩的单位是“牛 米”,也可以写成“焦”
答案:A
解析:解答:A、力矩是矢量,其大小不仅决定于力的大小,同时与矩心的位置有关,力矩的大小和方向决定着力对物体的转动作用,故A正确;
BC、当力的大小为零或力臂为零时,则力矩为零,此时力对物体没有产生转动的作用;故BC错误;
D、力矩的单位是N m或kN m,焦耳是力与位移的乘积,而力矩中的米是距离,不是位移,故D错误.
故选:A
分析:作用力使物体绕着转动轴或支点转动的趋向,称为力矩.力矩能够使物体改变其旋转运动.
二.填空题
16.如图所示,一根不均匀的铁棒AB与一辆拖车相连接,连接端B为一固定水平转动轴,拖车在水平面上做匀速直线运动,棒长为L,棒的质量为40kg,它与地面间的动摩擦因数为,棒的重心C距转动轴为,棒与水平面成30°角.运动过程中地面对铁棒的支持力为 N;若将铁棒B端的固定转动轴向下移一些,其他条件不变,则运动过程中地面对铁棒的支持力将比原来 (选填“增大”、“不变”或“减小”).
答案:200|增大
解析:解答:以B点为转轴,在拖车在水平面上向右做匀速直线运动过程中,棒的力矩平衡,设棒与水平面的夹角为α.则有mgcosα=NLcosα+fLsinα ①
又滑动摩擦力f=μN.
联立得:2mgcosα=3Ncosα+3μNsinα ②
解得,
α=30°代入解得,N=200N
若将铁棒B端的固定转动轴向下移一些,α减小,tanα减小,由③得知,N增大.
故答案为:200,增大.
分析:选取接端B为转动轴,地面对铁棒的支持力的力矩与重力的力矩平衡,写出平衡方程,即可求出地面对铁棒的支持力;若将铁棒B端的固定转动轴向下移一些则AB与地,地面之间的夹角减小,同样,可以根据力矩平衡的公式,判定地面对铁棒的支持力的变化.
17.如图,重为G的物体,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上.转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆AB和BC的质量不计,A、B、C三处均用铰链连接.当物体处于平衡状态时,杆AB所受力的大小为 ,杆BC所受力的大小为 .
答案:2.73G|3.73G
解析:解答:以A为支点,AB受到BC的支持力和两个绳子的拉力,它们的力臂如图1,设AB杆的长度为L,则:
竖直向下的拉力的力臂;L1=L
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL1+GL2=FBC L3
代入数据得:FBC=3.73G
同理,以C为支点,BC受到AB的拉力和两个绳子的拉力,它们的力臂如图2,则:
竖直向下的拉力的力臂:;
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL4+GL5=FAB L6
代入数据得:FAB=2.73G
故答案为:2.73G;3.73G
分析:画出各个力,分别作出各个力的力臂,然后又力矩的平衡即可解答.
18.重为G的均匀直杆AB一端用铰链与墙相连,另一端用一条通过光滑的小定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=AB.滑轮与绳重力不计.则B点处绳子的拉力的大小是 N,轴对定滑轮M的作用力大小是 N.
答案:|
解析:解答:杆处于力矩平衡状态,设绳子的拉力为F,杆长为L,则由力矩平衡条件可知:
G=F +F;
解得:F=;
滑轮受两绳的拉力及轴对定滑轮的作用力而处于平衡,即轴对定滑轮的作用力与两边绳子的拉力相等,则由力的平行四边形可求得两拉力的合力即为定滑轮对轴的作用力:
由几何关系可知:
而轴对定滑轮的作用力与F'大小相等,方向相反;
故答案为:;
分析:由受力分析可知,杆受B点绳子的拉力、C点绳子的拉力及本身的重力作用处于转动平衡状态;由力矩平衡条件可求得绳子的拉力;由力的合成可求得轴对定滑轮的作用力.
19.如图所示,为一水阀的示意图,C为轻活塞,截面积为10cm2,AB是长为0.8m的轻质杠杆,O为转轴,AO的长度为0.2m,各接触处均光滑.已知大气压强为1.0×105Pa,自来水管内的压强为2.5×105Pa.为保持AB杆水平而水不流出,则在B端需挂一质量为 kg的重物,此时转轴对杆的作用力大小为 N.
答案:5|200
解析:解答:根据力矩平衡知(PS﹣P0S) AO=mg OB
则
对O受力分析知转轴对杆的作用力大小
F=mg+(P﹣P0)S=50N+(2.5﹣1)×105×10×10﹣4N=200N
故答案为:5 200
分析:根据力矩平衡知(PS﹣P0S) AO=mg OB求解质量m,根据力与平衡求解转轴对杆的作用力.
20.半径分别为r和2r的两个质量不计的圆盘,共轴固定连结在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个质量为m的质点,小圆盘上绕有细绳.开始时圆盘静止,质点处在水平轴O的正下方位置.现以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度时,质点m的速度最大,则恒力F= ;若圆盘转过的最大角度则此时恒力F= .
答案:mg|
解析:解答:以水平恒力F拉细绳,使两圆盘转动,若两圆盘转过的角度时,质点m的速度最大,此时力矩平衡,故:
F r=mg 2rsin30°
解得:F=mg;
根据能量守恒定律得
解得
本题答案是:mg,.
分析:两圆盘转过的角度θ时,两个物体构成的系统减小的重力势能等于增加的动能,根据机械能守恒定律列式求解;当F的力矩大于mg的力矩时,质点m的速度增大,当F的力矩小于mg的力矩时,质点m的速度减小,则当两者力矩相等时,质点m的速度最大.根据力矩平衡条件列方程求解.再能量守恒定律求解F.
21.可轻杆OA绕转轴O自由转动,用轻绳AB和轻弹簧BC连接,位置如图所示.将质量m的小物块悬挂在轻杆中点处,静止后OA处在水平位置,轻绳AB伸直但无拉力,则此时弹簧上的弹力大小为 ;将m右移OA/4的距离,轻绳上拉力大小为 .
答案:|
解析:解答:设OA长为l,当绳无拉力,则弹簧的拉力的力矩与重力的力矩平衡,即:Flocsin60°=mg;
当m右移的距离时,由力矩平衡得:Flocsin60°+Tlsin30°=mg;
解得:
答案为:
分析:杠杆平衡的条件:动力乘以动力臂等于阻力乘以阻力臂;如图所示,根据直角三角形角与边的关系,求出绳子对杠杆拉力的力臂;再利用已知的重力和重力的力臂以及杠杆平衡的条件求出拉力F的大小.
三.解答题
22.改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm.
(1)(多选题)做这样改进的优点是( )
A.力传感器既可测拉力又可测压力
B.力传感器测力时不受主观判断影响,精度较高
C.能消除转轴摩擦引起的实验误差
D.保证力传感器所受拉力方向不变
答案:BF
(2)某同学用该装置做实验,检验时发现盘停止转动时G点始终在最低处,他仍用该盘做实验.在对力传感器进行调零后,用力传感器将力矩盘的G点拉到图示位置,此时力传感器读数为3N.再对力传感器进行调零,然后悬挂钩码进行实验.此方法 (选填“能”、“不能”)消除力矩盘偏心引起的实验误差.已知每个钩码所受重力为1N,力矩盘按图示方式悬挂钩码后,力矩盘所受顺时针方向的合力矩为 N m.力传感器的读数为 N.
答案:能|0.7|﹣0.5
解析:解答:(1)A、弹簧可以测拉力和压力,故A错误;
B、力传感器,定滑轮固定在横杆上,替代原装置中的弹簧秤,主要好处是:力传感器测力时,不受主观判断影响,精确度高和保证力传感器所受拉力方向不变,故BD正确;
C、不能消除转轴摩擦力引起的误差,故C错误;
故选:BD.(2)某同学该装置做实验,检验时发现盘停止转动时,他仍用该盘做实验,在对力传感器进行调零后,用力传感器将力矩盘的G点拉到图示位置,此时力传感器读数为3N,说明此时偏心的顺时针力矩M0=3×2×0.05N m=0.3N m;
再对力传感器进行调零,这时就可以消除力矩盘的偏心引起实验误差,力矩盘所受顺时针方向合力矩M1=2×1×0.05﹣2×1×3×0.05﹣0.3N m=0.7N m;
根据固定转动轴物体平衡条件,则有:
F×2×0.05+3×1×3×0.05﹣0.3=2×1×0.05﹣2×2×3×0.05﹣0.3;
解得:F=﹣0.5N;
故答案为:(1)BF;(2)能,0.7,﹣0.5.
分析:(1)根据弹簧可以拉伸与压缩,结合实验原理,及操作步骤,即可求解;(2)根据力矩公式,结合力传感器读数,求得偏心的顺时针力矩,再消除力矩盘的偏心引起实验误差,求得力矩盘所受顺时针方向合力矩,从而根据平衡条件,即可求解.
23.用如图所示装置做“研究有固定转动轴物体平衡条件“的实验,力矩盘上个同心圆的间距相等.
(1)(多选)在用细线悬挂钩码前,以下哪些措施是必要的
A.判断力矩盘是否在竖直平面 B.判断横杆MN是否严格保持水平
C.判断力矩盘与转轴间的摩擦是否足够小 D.判断力矩盘的重心是否位于盘中心
答案:ACD
(2)在A、B、C三点分别用细线悬挂钩码后,力矩盘平衡,如图所示,已知每个钩码所受的重力为1牛,则此时弹簧称示数为 牛.
答案:4
(3)由于力矩盘偏心未经调整实际测出的弹簧称读数偏大,则力矩盘的重心在轴的 .(填左方或右方)
答案:右方
解析:解答:(1)A、为了防止细线及弹簧称与力矩盘摩擦,判断力矩盘是否处在竖直平面是必要的.故A正确.
B、本实验与横杆MN是否平衡无关,没有必要检查横杆MN是否严格保持水平.故B错误.
C、D、本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系,重力、摩擦力等影响要尽可能小,故CD正确.
故选:ACD.(2)设A、B、C三处拉力大小分别为FA、FB、FC,弹簧称示数为F,由题
FA=1N,FB=1N,FC=3N
设力矩盘上相邻同心圆间距为r,则弹簧称拉力的力臂为L=2r
根据力矩平衡得:
FA 2r+FL=FB r+FC 3r
代入解得:F=4N;(3)由于力矩盘偏心未经调整实际测出的弹簧称读数偏大,因此力矩盘重心在轴的右方,才会导致弹簧秤实际读数偏大,
故答案为:(1)ACD(2)4;(3)右方.
分析:(1)本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系,要尽可能减小其他力的影响,比如重力、摩擦力等影响.根据此要求分析选择.(2)分别确定A、B、C三点细线拉力大小和力臂大小,根据力矩平衡求出弹簧称拉力;(3)根据力矩盘心在轴的某一方,结合力矩平衡条件,即可得出弹簧称实际读数偏大还是偏小.
24.在研究有固定转动轴物体平衡条件的实验中
(1)实验开始前需要检查力矩盘重心是否在转轴处,描述检查的操作过程.
答案:心在转轴上,力矩盘本身的重力才可以忽略不计,转动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上
(2)某同学采用50g的钩码,力矩盘平衡后如图所示,弹簧秤读数1.1N,盘面中3个同心圆半径分别是2cm、4cm、6cm.填写下表(g取9.8m/s2,答案精确到0.001N m):
顺时针力矩 逆时针力矩
0.059N m
答案: 0.064N m
解析:解答:(1)心在转轴上,力矩盘本身的重力才可以忽略不计,转动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上;(2)逆时针力矩为M=1.1×4×10﹣2+50×10﹣3×10×4×10﹣2=0.064N m.
故答案为:(1)在任意位置(转过任意角度)能静止/平衡.(2)0.064N m
分析:(1)动后,停下时事先的标记能够处于任意位置,即转盘能随遇平衡,说明转盘的重心在转轴上;(2)簧秤读数1.1N,一个钩码重50g,根据力矩等于力与力臂的乘积.
25.如图所示是一个半径为R的轮子,它绕固定转动轴O顺时针方向转动,两侧各有一个长为L的竖直杆MO和NQ,它们都固定在天花板上M、N处(如图所示).两轻杆上距轴为a处各固定一宽度为b的摩擦块(上下厚度不计).摩擦块与轮子间动摩擦因数都是μ(μ<),不计杆与摩擦块的重力.为使轮子刹停,在两杆下端P、Q之间用轻绳悬挂一重物.刚好使三根细绳之间夹角都相等.
(1)有同学认为:“由于该装置高度对称,所以两边摩擦力的大小是相等的”.你认为这位同学的看法是否正确?为什么(请简要说明你的理由)?
答案:这位同学的看法是不正确,因为受力(或力矩)情况并不对称;
(2)设AP和AQ上的拉力的大小都是F,则左、右两侧摩擦力作功之比是多少?
答案:设AP和AQ上的拉力的大小都是F,则左、右两侧摩擦力作功之比是;
(3)为使轮子在规定的时间内能停下,规定制动力矩的大小为M.求此时在下方悬挂物体的重力G是多大?
答案:为使轮子在规定的时间内能停下,规定制动力矩的大小为M.此时在下方悬挂物体的重力G是
解析:解答:(1)这位同学的看法是不正确,因为受力(或力矩)情况并不对称. (2)对左侧的杆进行受力分析如图,摩擦力与拉力产生逆时针方向的力矩,支持力N1产生顺时针方向的力矩,根据力矩平衡得:μN1b+Fcos30°L=N1a
代入数据解得:
同理对右侧的杆进行受力分析如图,摩擦力与拉力产生顺时针方向的力矩,支持力N1产生逆时针方向的力矩,根据力矩平衡得:μN2b+N2a=FLcos30°
代入数据得:
轮子停下的过程中,两侧的路程相同,根据W=FS
所以:(3)由题图可知,轮子制动的过程中,受到的两侧的摩擦力的方向都与轮子边缘的质点运动的方向相反,所以轮子制动的力矩的方向与轮子转动的方向相反,制动的力矩大小:
联立解得:
分析:(1)(2)分别对左右两侧的杆进行受力分析,结合力矩平衡即可求出左右两侧受到的摩擦力,从而判断出两侧的摩擦力是否相等;再结合功的计算公式即可求出左、右两侧摩擦力作功之比.(3)对轮子进行受力分析,求出轮子受到的摩擦力的力矩的表达式,然后结合(2)中的摩擦力的表达式即可求出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 22 页 (共 23 页) 版权所有@21世纪教育网
