人教版物理高二选修2-3第五章第四节射线的探测和防护同步训练
文档属性
| 名称 | 人教版物理高二选修2-3第五章第四节射线的探测和防护同步训练 |

|
|
| 格式 | doc | ||
| 文件大小 | 635.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-05-26 10:32:50 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
人教版物理高二选修2-3第五章
第四节射线的探测和防护同步训练
一.选择题
1.如图所示的阴极射线管的玻璃管内已经抽成真空,当左右两个电极连接到高压电源时,阴极会发射电子,电子在电场的加速下飞向阳极,挡板上有一个扁平的狭缝,电子飞过挡板后形成一个扁平的电子束,长条形的荧光板在阳极端稍稍倾向轴线,电子束掠射到荧光板上,显示出电子束的径迹,现在用该装置研究磁场对运动电荷的作用的实验,下列对该实验的说法正确的是( )
A.没有施加磁场时,电子束的径迹是一条抛物线
B.若图中左侧是阴极射线管的阴极,加上图示的磁场,电子束会向上偏转
C.施加磁场后,根据电子束在磁场中运动径迹和磁场方向,可由相关知识判断出阴极射线管两个电极的极性
D.施加磁场后,结合阴极射线管的两个电极的极性和电子束在磁场中运动的径迹,可以判断出磁场的方向,但无法判断出磁场的强弱
答案:C
解析:解答:A、没有施加磁场时,电子束只受电场离,在电场力作用下做加速直线运动,故A错误;
B、因为左边是阴极,右边是阳极,所以电子在阴极管中的运动方向是左到右,产生的电流方向是右到左(注意是电子带负电),根据左手定则,四指指向左,手掌对向N极(就是这个角度看过去指向纸面向里),此时大拇指指向下面,所以电子在洛伦兹力作用下轨迹向下偏转,故B错误;
C、根据轨迹和左手定则即可判断阴极射线管两个电极的极性,故C正确;
D、施加磁场后,结合阴极射线管的两个电极的极性和电子束在磁场中运动的径迹,可以判断出磁场的方向,根据曲率半径可判断出磁场强弱,故D错误;
故选:C
分析:此题要求要了解电子射线管的构造和原理,阴极是发射电子的电极,电子在磁场中运动,受到洛伦兹力的作用而发生偏转.从而显示电子运动的径迹,偏转方向有左手定则判断;根据曲率半径可判断磁场强弱;
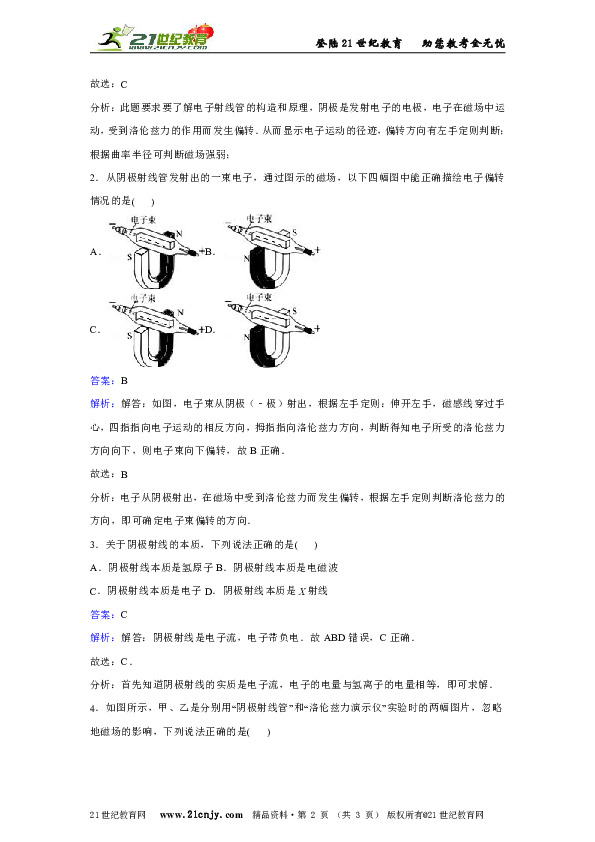
2.从阴极射线管发射出的一束电子,通过图示的磁场,以下四幅图中能正确描绘电子偏转情况的是( )
A.B.
C.D.
答案:B
解析:解答:如图,电子束从阴极(﹣极)射出,根据左手定则:伸开左手,磁感线穿过手心,四指指向电子运动的相反方向,拇指指向洛伦兹力方向,判断得知电子所受的洛伦兹力方向向下,则电子束向下偏转,故B正确.
故选:B
分析:电子从阴极射出,在磁场中受到洛伦兹力而发生偏转,根据左手定则判断洛伦兹力的方向,即可确定电子束偏转的方向.
3.关于阴极射线的本质,下列说法正确的是( )
A.阴极射线本质是氢原子B.阴极射线本质是电磁波
C.阴极射线本质是电子D.阴极射线本质是X射线
答案:C
解析:解答:阴极射线是电子流,电子带负电.故ABD错误,C正确.
故选:C.
分析:首先知道阴极射线的实质是电子流,电子的电量与氢离子的电量相等,即可求解.
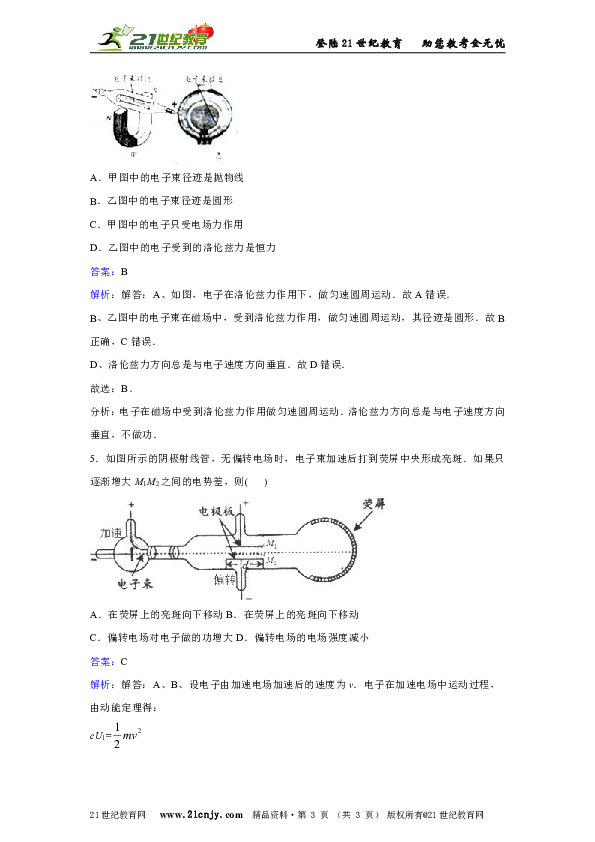
4.如图所示,甲、乙是分别用“阴极射线管”和“洛伦兹力演示仪”实验时的两幅图片,忽略地磁场的影响,下列说法正确的是( )
A.甲图中的电子束径迹是抛物线
B.乙图中的电子束径迹是圆形
C.甲图中的电子只受电场力作用
D.乙图中的电子受到的洛伦兹力是恒力
答案:B
解析:解答:A、如图,电子在洛伦兹力作用下,做匀速圆周运动.故A错误.
B、乙图中的电子束在磁场中,受到洛伦兹力作用,做匀速圆周运动,其径迹是圆形.故B正确,C错误.
D、洛伦兹力方向总是与电子速度方向垂直.故D错误.
故选:B.
分析:电子在磁场中受到洛伦兹力作用做匀速圆周运动.洛伦兹力方向总是与电子速度方向垂直,不做功.
5.如图所示的阴极射线管,无偏转电场时,电子束加速后打到荧屏中央形成亮斑.如果只逐渐增大M1M2之间的电势差,则( )
A.在荧屏上的亮斑向下移动B.在荧屏上的亮斑向下移动
C.偏转电场对电子做的功增大D.偏转电场的电场强度减小
答案:C
解析:解答:A、B、设电子由加速电场加速后的速度为v.电子在加速电场中运动过程,由动能定理得:
eU1=
解得,v=.
电子进入偏转电场后做匀变速曲线运动,沿极板方向做匀速直线运动,沿电场线方向做初速度为零的匀加速直线运动,则有:
水平方向有:L=vt
竖直方向有:a=
v=at
电子刚离开偏转电场时的偏转角正切为:tanα=
由以上各式解得:电子刚离开偏转电场时偏转角的正切为:tanα=,
则α=arctan.
即电子离开偏转电场时的偏转角α随偏转电压的增大而增大.如果只逐渐增大M1M2之间的电势差U2,在荧屏上的亮斑向上移动.故A不正确,B错误;
C、电子离开偏转电场时的偏转量:y==,
如果只逐渐增大M1M2之间的电势差U2,电子离开偏转电场时的偏转量将增大.
偏转电场对电子做的功:W=e E y,偏转量越大,电场力做的功越多.故C正确;
D、偏转电场的电场强度:E=,所以如果只逐渐增大M1M2之间的电势差U2,偏转电场的电场强度增大.故D错误.
故选:C
分析:电子在加速电场中运动时,电场力做正功,电子获得速度,根据动能定理求解电子离开加速电场后的速度;
电子垂直进入偏转电场后做类平抛运动,平行于极板方向做匀速直线运动,垂直于极板方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式求得偏转量的表达式与电场力做功的表达式,即可进行说明.
6.下列说法正确的是( )
A.阴极射线和β射线本质上都是电子流,都来自于原子的核外电子
B.温度越高,黑体辐射强度的极大值向频率较小的方向移动
C.天然放射现象的发现,让人们知道原子核是组成物质的最小微粒
D.公安机关对2014年5月初南京丢失铱﹣192放射源的4名责任人采取强制措施是因为该放射源放出大剂量的射线会污染环境和危害生命.
答案:D
解析:解答:A、阴极射线和β射线本质上都是电子流,阴极射线来自原子的核外电子,而β射线是由原子核中中子转化而来的,故A错误.
B、温度越高,黑体辐射强度的极大值向频率较大的方向移动;故B错误.
C、天然放射现象的发现,让人们知道原子核具有复杂结构,不是组成物质的最小微粒.故C不正确.
D、放射源放出大剂量的射线会污染环境和危害生命;故D正确.
故选:D
分析:β粒子来源于原子核中中子的转化;温度越高,黑体辐射强度的极大值向频率较大的方向移动;天然放射现象的发现,让人们知道原子核不是组成物质的最小微粒;放射源放出大剂量的射线会污染环境和危害生命;在光电效应现象中,光电流的饱和值会随着光照强度的增大而增大.
7.如图所示,阴极射线示波管的聚集电场是由电极A1、A2形成,实线为电场线,虚线为等势线,z轴为该电场的中心轴线,P、Q、R为一个从左侧进入聚焦电场的电子运动轨迹上的三点,则下列说法不正确的是( )
A.电极A1的电势低于电极A2的电势
B.电子在P点处的动能大于在Q点处的动能
C.电场中Q点的电场强度大于R点的电场强度
D.电子从P至R的运动过程中,电场力对它一直做正功
答案:D
解析:解答:A、沿电场线电势降低,因此电极A1的电势低于电极A2,故A错误;
B、电子从P至R的运动过程中,是由低电势向高电势运动时,电场力做正功,动能增加,电势能减小,故B错误,D正确;
C、等势线密的地方电场线也密,因此Q点电场线比R点电场线密,故Q点的电场强度大于R点的电场强度,因此C错误,
故选:D.
分析:沿电场线电势降低,电场强度的大小与电场线的疏密的关系;明确电子在电场中的受力特点以及电场力做功情况,从而进一步判断电势能、动能等变化情况.
8.如图为电视机显像管中电子束偏转的示意图.磁环上的偏转线圈通以图示方向的电流时,沿轴线向纸内射入的电子束的偏转方向( )
A.向上B.向左C.向下D.向右
答案:B
解析:解答:磁环上的偏转线圈通以图示方向的电流时,根据安培定则,在磁环上形成的磁场方向竖直向下,磁场是闭合的,故在磁环中心处的磁场是竖直向上的,在根据左手定则,当电子束沿轴线向纸内射入时,电子束受到向左的洛伦兹力,故电子束的偏转方向向左.故B正确、ACD错误.
故选:B.
分析:将整个线圈当成左右两部分研究,因为绕向变化,结合安培定则判断出磁场方向,由左手定则分析判断电子束所受的洛伦兹力方向,即可判断偏转方向.
9.如图所示,阴极射线管接通电源后,电子束由阴极沿x轴正方向射出,在荧光板上会看到一条亮线.要使荧光板上的亮线向z轴负方向偏转,可采用的方法是( )
A.加一沿y轴负方向的磁场B.加一沿z轴正方向的磁场
C.加一沿y轴正方向的电场D.加一沿z轴负方向的电场
答案:A
解析:解答:A、若加一沿y轴负方向的磁场,根据左手定则,洛伦兹力方向沿z轴负方向,亮线向下偏转,故A正确;
B、若加一沿z轴正方向的磁场,根据左手定则,洛伦兹力方向沿y轴负方向,亮线向y轴负方向偏转,故B错误;
C、若加一沿y轴正方向的电场,电子受电场力作用向外,亮线向y轴负方向偏转,故C错误.
D、若加一沿z轴负方向的电场,电子受到的电场力沿z轴的正方向,亮线向上偏转,故D错误.
故选:A.
分析:电子射线由阴极沿x轴方向射出,形成的亮线沿z轴正方向偏转,说明电子受到的洛伦兹力方向向下,将四个选项逐一代入,根据左手定则判断分析,选择可行的磁场方向
10.阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
A.电极A1的电势高于电极A2的电势
B.电场中Q点的电场强度大于R点的电场强度
C.电子在R点处的动能大于在P点处的动能
D.若将一束带正电的粒子从左侧射入聚焦电场也一定被会聚焦
答案:C
解析:解答:A、根据电场线与等势线垂直,可知管轴上电场线方向向左.根据沿电场线电势降低,得知电极A1的电势低于电极A2,故A错误;
B、等差等势线密的地方电场线也密,因此Q点电场线比R点电场线疏,故Q点的电场强度小于R点的电场强度,故B错误;
C、电子从低电势向高电势运动时,电场力做正功,动能增加,所以电子在R点处的动能大于在P点处的动能,故C正确.
D、若将一束带正电的粒子从左侧射入聚焦电场,所受的电场力向外侧,不可能会聚,故D错误.
故选:C.
分析:沿电场线电势降低,电场强度的大小与电场线的疏密的关系;明确电子在电场中的受力特点以及电场力做功情况,从而进一步判断电势能、动能等变化情况.根据正粒子所受的电场力方向,判断能否会聚.
11.放射性同位素发出的射线在科研、医疗、生产等诸多方面得到了广泛的应用,下列有关放射线应用的说法中正确的有( )
A.放射线改变了布料的性质使其不再因摩擦而生电,因此达到消除有害静电的目的
B.利用γ射线的贯穿性可以为金属探伤,也能进行人体的透视
C.用放射线照射作物种子能使其DNA发生变异,其结果一定是成为更优秀的品种
D.用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的危害
答案:D
解析:解答:A、利用放射线消除有害静电是利用α射线的电离性,使空气分子电离成导体,将静电放出,故A错误;
B、利用γ射线的贯穿性可以为金属探伤,γ射线对人体细胞伤害太大,因此不能用来人体透视,故B错误;
C、DNA变异并不一定都是有益的,也有时发生变害的一面,故C错误;
D、γ射线对人体细胞伤害太大,在用于治疗肿瘤时要严格控制剂量,故D正确;
故选:D.
分析:α射线使空气分子电离成导体,将静电放出;变异并不一定都是有益的;γ射线对人体细胞伤害大.
12.下列关于电磁污染的说法,不正确的是( )
A.电磁污染主要是指电磁辐射
B.电磁辐射会干扰其他仪器的正常工作
C.电磁辐射对人体和动物都有危害
D.频率越高的电磁波,电磁辐射的危害就越小
答案:D
解析:解答:A、电磁污染主要是指各种电磁辐射;如手机、雷达等;故A正确;
B、电磁辐射会干扰其他仪器并能人和动物造成伤害;故BC正确;
D、频率越高的电磁波,电磁辐射的危害就越大;故D错误;
本题选错误的;故选:D.
分析:各种电器在工作中均会造成电磁辐射,从而对环境造成污染!频率越高,电磁辐射远严重.
13.用α粒子轰击时,得到,同时放出一种粒子,关于这种粒子,下列说法中正确的是( )
A.它来自于原子核
B.它能穿透几厘米厚的铅板
C.它垂直进入磁场中不发生偏转
D.它是一种频率很高的光子
答案:A
解析:解答:A、根据核反应过程中的质量数和电荷数守恒可知该未知粒子的质量数和电荷数都为1,即该未知粒子为质子,带正电;核反应是原子核的反应,故它来自于原子核,故A正确;
B、质子流不能穿透几厘米厚的铅板,只有γ射线可以穿透几厘米厚的铅板,故B错误;
C、它垂直进入磁场中,会做匀速圆周运动,故C错误;
D、根据核反应过程中的质量数和电荷数守恒可知该未知粒子的质量数和电荷数都为1,即该未知粒子为质子,带正电,故D错误;
故选A.
分析:根据核反应的质量数和电荷数守恒,判断出未知粒子的质量数和电荷数即可明确该未知粒子的性质.
14.下列应用中把放射性同位素不作为示踪原子的是( )
A.利用含有放射性碘131的油,检测地下输油管的漏油情况
B.把含有放射性元素的肥料施给农作物,利用探测器的测量,找出合理的施肥规律
C.利用射线探伤法检查金属中的砂眼和裂纹
D.给怀疑患有甲状腺的病人注射碘131,诊断甲状腺的器质性和功能性疾病
答案:C
解析:解答:A、利用含有放射性碘131的油,检测地下输油管的漏油情况,是利用碘131的放射性,即将碘131作为示踪原子,故A正确;
B、把含有放射性元素的肥料施给农作物,利用探测器的测量,找出合理的施肥规律,是示踪原子的运用,故B正确;
C、利用射线探伤法检查金属中的砂眼和裂纹,是利用γ射线穿透能力强,不是示踪原子的运用,故C错误;
D、给怀疑患有甲状腺的病人注射碘131,诊断甲状腺的器质性和功能性疾病,是将碘131作为示踪原子,故D正确;
故选:C.
分析:放射性同位素碘131能做示踪原子;γ射线穿透能力强,通常会用于工业探伤.
15. 2011年3月11日,日本大地震引发了福岛核电站核泄漏事故,下列关于核电站的说法正确的是( )
A.核电站利用核聚变反应时释放的能量进行发电
B.核电站利用海洋的潮汐能发电
C.核能是可再生能源
D.核泄漏释放的放射性物质发出的射线对人体是有危害的
答案:D
解析:解答:目前核电站均采用重核裂变进行进行的,故AB错误;
核能是利用重核裂变进行的,是不可再生资源,故C错误;
长时间接受核辐射会使正常细胞发生癌变,故D正确.
故选D.
分析:正确解答本题要了解核能的应用以及放射性的污染和防护,同时了解裂变和聚变的区别.
二.填空题
16.如图所示,电子射线管(A为其阴极),放在蹄形磁铁的N、S两极间(图中C为N极),射线管的A、B两极分别接在直流高压电源的负极和正极.此时,荧光屏上的电子束运动径迹 偏转(填“向上”“向下”或“不”).
答案:向下
解析:解答:据题因为A是阴极,B是阳极,所以电子在阴极管中的运动方向是A到B,产生的电流方向是B到A(注意是电子带负电),根据左手定则,四指由B指向A,掌心对着N极此时拇指向下,所以电子束所受的洛伦兹力向下,轨迹向下偏转.
故答案为:向下
分析:此题要求要了解电子射线管的构造和原理.阴极是发射电子的电极,要接到高压的负极上,电子在磁场中运动,受到洛伦兹力的作用而发生偏转.从而显示电子运动的径迹,偏转方向有左手定则判断.
17.如图所示,把一电子射线管放在蹄形磁铁的两极之间,当电子由“﹣”,极射向“+”极时,将向 方偏转(填“上”或“下”).
答案:下
解析:解答:电子从阴极射向阳极,根据左手定则,磁感线穿入手心,四指指向电子运动的反方向,洛伦兹力的方向向下,则电子束向下偏转.
故答案为:下.
分析:阴极射线管电子从阴极射向阳极,运用左手定则判断电子束受到的洛伦兹力的方向,来判断电子束偏转的方向.
18.如图所示,电子枪射出的电子束进入示波管,在示波管正下方有竖直放置的通电环形导线,则示波管中的电子束将 偏转.(填“向上”“向下”“向里”“向外”)
答案:向上
解析:解答:由安培定则可知,在示波管下方环形电流的磁场在环形区域内磁感线方向垂直纸面向里,根据磁感线是闭合的曲线可知,在环形电流外侧磁感线方向垂直纸面向外;
电子束由左向右运动,电子束形成的电流方向水平向左,
由左手定则可知,电子束受到的安培力竖直向上,则电子束向上偏转;
故答案为:向上.
分析:由安培定则判断出环形导线中的电流在示波管位置的磁场方向;然后由左手定则判断出电子束受到的安培力方向,最后根据电子束的受力方向判断电子束如何偏转.
19.如图是阴极射线管的示意图.接通电源后,会有电子从阴极K射向阳极A,并在荧光屏上形成一条亮线.要使荧光屏上的亮线向下偏转,则可以加一个方向平行纸面 (填“向上”或“向下”)的电场,或者加一个方向垂直纸面 (填“向里”或“向外”)的磁场.
答案:向上|向里
解析:解答:由题意,根据正电荷受力与电场方向相同,若加一方向平行纸面向上的电场,电场力使得电子向下偏转.
若加一方向垂直纸面向里的磁场,根据左手定则,洛伦兹力方向竖直向下,亮线向下偏转.
故答案为:向上,向里.
分析:电子射线由阴极沿x轴方向射出,形成的亮线向下偏转,说明电子受到的洛伦兹力方向向下,根据左手定则判断分析,选择可行的磁场方向;或电子受到向下的电场力,从而确定电场强度的方向.
20.示波管应用了 (填“电场”或“磁场”)使电子束偏转的原理;纯电阻电路中,电动势为E,内电阻为r的电源的最大输出功率为 .
答案:电场|
解析:解答:示波管应用了电场使电子束偏转的原理.
根据数学知识分析可知,当外电阻等于电源的内电阻时,电源的输出功率最大,此时电路中电流为:I=,电源的最大输出输出功率为:Pm=I2R=I2r=.
故答案为:电场,.
分析:示波管应用了电场使电子束偏转的原理.当外电阻等于电源的内电阻时,电源的输出功率最大,由闭合电路欧姆定律和功率公式求出电源的最大的输出功率.
三.解答题
21.在电脑显示器的真空示波管内,控制电子束扫描的偏转场是匀强磁场,磁场区域是宽度为3.0cm的矩形,右边界距荧光屏20.0cm,高度足够.某段时间内磁场方向垂直纸面向外,磁感应强度B=4.55×10﹣3T不变.电子初速度不计,经U=4550V电压加速后沿中心线射入磁场,偏转后打在屏上产生亮点(若无磁场,亮点在屏中心),已知电子的质量m=0.91×10﹣30kg,电荷量e=1.6×10﹣19C.
(1)在图中大致图出电子运动的径迹;
答案:
(2)求亮点偏离荧光屏中心的距离.
答案:电子经U加速得到速度v0
由eU=
得v0==M/s=4×107m/s.
由evB=得①
R==0.05m=5cm②
sinα=0.6,cosα=0.8,tanα=0.75③
亮点偏离屏中心的距离:
y=(r﹣rcosα)+20.0tanα=5×(1-0.8)cm+20.0×cm=16cm;
解析:解答:(1)电子运动的径迹如图所示:
(2)电子经U加速得到速度v0
由eU=
得v0==M/s=4×107m/s.
由evB=得①
R==0.05m=5cm②
sinα=0.6,cosα=0.8,tanα=0.75③
亮点偏离屏中心的距离:
y=(r﹣rcosα)+20.0tanα=5×(1-0.8)cm+20.0×cm=16cm;
答:(1)在图中大致图出电子运动的径迹如图;(2)亮点偏离荧光屏中心的距离为16cm.
分析:(1)电子在电场中做直线运动,在磁场中由左手定则判断洛伦兹力方向向上,则电子向上偏转;(2)先由动能定理求出粒子离开电场时获得的速度,然后由牛顿第二定律求出粒子在磁场中圆周运动的半径,亮点偏离荧光屏中心的距离为磁场中竖直方向偏离的距离与做匀速直线运动过程竖直方向的位移之和.
22.汤姆孙测定电子比荷的实验装置如图甲所示.从阴极K发出的电子束经加速后,以相同速度沿水平中轴线射入极板D1、D2区域,射出后打在光屏上形成光点.在极板D1、D2区域内,若不加电场和磁场,电子将打在P1点;若只加偏转电压U,电子将打在P2点;若同时加上偏转电压U和一个方向垂直于纸面向外、磁感应强度大小为B的匀强磁场(图中未画出),电子又将打在P1点.已知极板长度为L,极板间距为d.忽略电子的重力及电子间的相互作用.
(1)求电子射人极板D1、D2区域时的速度大小;
答案:电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有:
evB=eE①
两极板间电场强度:E=②
解得:
v=③
(2)打在P2点的电子,相当于从D1、D2中轴线的中点O′射出,如图乙中的O′P2所示,已知∠P2O′P1=θ试推导出电子比荷的表达式;
答案:由几何关系得电子射出电场时竖直方向的侧移量:
y=tan8④
根据牛顿第二定律,有:=ma⑤
根据分位移公式,有:
L=vt⑥
y=⑦
又v=
联立各式得到:=⑧
(3)若两极板间只加题中所述的匀强磁场,电子在极板间的轨迹为一段圆弧,射出后打在P3点.测得圆弧半径为2L、P3与P1间距也为2L,求图乙中P1与P2点的间距a.
答案:如图所示,极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后做匀速直线运动,已知r=2L,由几何关系得到:α=30°⑨
射出磁场后水平方向的距离:
x==3L(10)
解得:
a=(+3L)tanθ=
解析:解答:(1)电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有:
evB=eE①
两极板间电场强度:E=②
解得:
v=③(2)由几何关系得电子射出电场时竖直方向的侧移量:
y=tan8④
根据牛顿第二定律,有:=ma⑤
根据分位移公式,有:
L=vt⑥
y=⑦
又v=
联立各式得到:=⑧(3)如图所示,极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后做匀速直线运动,已知r=2L,由几何关系得到:α=30°⑨
射出磁场后水平方向的距离:
x==3L(10)
解得:
a=(+3L)tanθ=
答:(1)电子射人极板D1、D2区域时的速度大小为;(2)电子比荷的表达式为为=;(3)图乙中P1与P2点的间距a为.
分析:(1)当电子在极板D1、D2间受到电场力与洛伦兹力平衡时,做匀速直线运动,受力平衡,由平衡条件可求出电子运动速度.(2)极板间仅有偏转电场时,电子在电场中做类平抛运动,将运动分解成沿电场强度方向与垂直电场强度方向的分运动,然后由牛顿第二定律和运动学公式列式后联立求解,从而可以求出电子比荷的表达式.(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,画出电子运动的轨迹,根据几何知识求解y.
23.在电子显像管内部,当未加偏转磁场时,电子枪打出的电子应沿直线运动打在荧光屏的正中心.但由于地磁场对带电粒子运动的影响,会出现在未加偏转磁场时电子束偏离直线运动的现象.已知电子质量为m=9.1×l0﹣31kg、元电荷e=1.6×l0﹣19C,从炽热灯丝发射出的电子(可视为初速度为零)经过加速电场加速动能是1.82×l04eV,沿水平方向由南向北运动.已知某地地磁场磁感应强度的竖直向下分量的大小为B=4.55×10﹣5T,地磁场对电子在加速过程中的影响可忽略不计.在未加偏转磁场的情况下,
(l)试判断电子束将偏向什么方向;
答案:根据左手定则,可以判断出电子束将偏向东方.
(2)求电子在该地磁场中运动的加速度的大小;
答案:设从加速电场射出的电子速度为v,据题有:Ek=,v==M/s=8×107m/s
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动,设电子的加速度为a,根据牛顿第二定律得:
evB=M
由以上各式解得:a==6.4×1014m/s2;
(3)若加速电场边缘到荧光屏的距离为l=40cm,试通过计算电子束的偏转位移说明该地磁场对电视画面有没有影响.(已知当|x|≤1时,=1-x)
答案:设电子在地磁场中运动的半径为R,
根据牛顿第二定律:evB=得R====10m
设电子在荧光屏上偏移的距离为x,根据图中的几何关系,有:
电子束的偏转位移d=R﹣=R-R=R[1﹣(1﹣ )]=R =10××M≈0.008m=8mm
所以该地磁场对电视画面有一定的影响,但不影响人们观看
解析:解答:(1)根据左手定则,可以判断出电子束将偏向东方.(2)设从加速电场射出的电子速度为v,据题有:Ek=,v==M/s=8×107m/s
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动,设电子的加速度为a,根据牛顿第二定律得:
evB=M
由以上各式解得:a==6.4×1014m/s2;(3)设电子在地磁场中运动的半径为R,
根据牛顿第二定律:evB=得R====10m
设电子在荧光屏上偏移的距离为x,根据图中的几何关系,有:
电子束的偏转位移d=R﹣=R-R=R[1﹣(1﹣ )]=R =10××M≈0.008m=8mm
所以该地磁场对电视画面有一定的影响,但不影响人们观看.
答:(1)电子束将偏向东偏;(2)电子在该地磁场中运动的加速度的大小为6.4×1014m/s2.(3)该地磁场对电视画面有一定的影响,但不影响人们观看.
分析:(1)电子在地磁场中受到洛伦兹力作用,根据左手定则判断出洛伦兹力的方向,即可知道电子束的偏转方向;(2)根据洛伦兹力等于向心力,列式求出电子在磁场中运动的加速度;(3)画出轨迹,根据几何知识求解打到荧光屏的电子与0点的距离.
24.汤姆孙测定电子比荷(电子的电荷量与质量之比)的实验装置如图所示.真空玻璃管内,阴极K发出的电子经加速后,穿过小孔A、C沿中心轴线OP1进入到两块水平正对放置的极板D1、D2间的区域,射出后到达右端的荧光屏上形成光点.若极板D1、D2间无电压,电子将打在荧光屏上的中心P1点;若在极板间施加偏转电压U,则电子将打P2点,P2与P1点的竖直间距为b,水平间距可忽略不计.若再在极板间施加一个方向垂直于纸面向外、磁感应强度为B的匀强磁场(图中未画出),则电子在荧光屏上产生的光点又回到P1点.已知极板的长度为L1,极板间的距离为d,极板右端到荧光屏间的距离为L2.忽略电子的重力及电子间的相互作用.
(1)求电子进入极板D1、D2间区域时速度的大小;
答案:电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有evB=eE
两极板间电场强度E=
解得v=
(2)推导出电子的比荷的表达式;
答案:极板间仅有偏转电场时,电子以速度v进入后,水平方向做匀速运动,在电场内的运动时间
电子在竖直方向做匀加速运动,设其加速度为a.
由牛顿第二定律有V=M
解得加速度a=
电子射出极板时竖直方向的偏转距离
电子射出极板时竖直方向的分速度为v=at1=
电子离开极板间电场后做匀速直线运动,经时间t2到达荧光屏,
电子在t2时间在竖直方向运动的距离y2=vyt2=
这样,电子在竖直方向上的总偏移距离b=y1+y2
解得电子比荷=
(3)若去掉极板D1、D2间的电压,只保留匀强磁场B,电子通过极板间的磁场区域的轨迹为一个半径为r的圆弧,阴极射线射出极板后落在荧光屏上的P3点.不计P3与P1点的水平间距,求P3与P1点的竖直间距y.
答案:极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,如答图所示.
则tan=
穿出磁场后在竖直方向上移动的距离y3=L2tan=
则y=r+y3-
解得y=r﹣
解析:解答:(1)电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有evB=eE
两极板间电场强度E=
解得v=(2)极板间仅有偏转电场时,电子以速度v进入后,水平方向做匀速运动,在电场内的运动时间
电子在竖直方向做匀加速运动,设其加速度为a.
由牛顿第二定律有V=M
解得加速度a=
电子射出极板时竖直方向的偏转距离
电子射出极板时竖直方向的分速度为v=at1=
电子离开极板间电场后做匀速直线运动,经时间t2到达荧光屏,
电子在t2时间在竖直方向运动的距离y2=vyt2=
这样,电子在竖直方向上的总偏移距离b=y1+y2
解得电子比荷=(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,如答图所示.
则tan=
穿出磁场后在竖直方向上移动的距离y3=L2tan=
则y=r+y3-
解得y=r﹣
答:(1)电子进入极板D1、D2间区域时速度的大小为;(2)电子的比荷的表达式为=;(3)P3与P1点的竖直间距y为r﹣.
分析:(1)当电子在极板D1、D2间受到电场力与洛伦兹力平衡时,做匀速直线运动,受力平衡,由平衡条件可求出电子运动速度.(2)极板间仅有偏转电场时,电子在电场中做类平抛运动,将运动分解成沿电场强度方向与垂直电场强度方向,然后由牛顿第二定律和运动学公式可求出偏转距离和离开电场时的速度.电子离开电场后,做匀速直线运动,从而可以求出偏转距离.(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,画出电子运动的轨迹,根据几何知识求解y.
25.电视机显像管简单原理如图所示,初速度不计的电子经加速电场加速后进入有限边界宽度为L的匀强磁场,磁感应强度为B,如要求电子束偏转角为α,已知电子电量为e,质量为m.
(1)画出整个过程的轨迹图;
答案:
(2)电子在磁场中运动的时间;
答案:根据电子做匀速圆周运动,则运动时间:t=
由T=
解得:t=;
(3)求加速电场的电势差U.
答案:电子经加速电场加速后,速度为v,
则由动能定理得:eU=mv2;
由几何关系得,电子运动半径:R=;
由牛顿第二定律,有:evB=;
由以上各式解得加速电压:U=
解析:解答:(1)电子现在加速电场中做匀加速直线运动,然后进入匀强磁场中作匀速圆周运动,轨迹如图;(2)根据电子做匀速圆周运动,则运动时间:t=
由T=
解得:t=;(3)电子经加速电场加速后,速度为v,
则由动能定理得:eU=mv2;
由几何关系得,电子运动半径:R=;
由牛顿第二定律,有:evB=;
由以上各式解得加速电压:U=;
答:(1)画出整个过程的轨迹图如上所示;(2)电子在磁场中运动的时间t=;(3)求加速电场的电势差U=.
分析:(1)根据电场力与洛伦兹力方向,结合力与运动的关系,从而即可求解;(2)根据电子的运动周期,结合圆心角,即可求解;(3)根据动能定理与牛顿第二定律,结合几何关系,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 23 页 (共 24 页) 版权所有@21世纪教育网
人教版物理高二选修2-3第五章
第四节射线的探测和防护同步训练
一.选择题
1.如图所示的阴极射线管的玻璃管内已经抽成真空,当左右两个电极连接到高压电源时,阴极会发射电子,电子在电场的加速下飞向阳极,挡板上有一个扁平的狭缝,电子飞过挡板后形成一个扁平的电子束,长条形的荧光板在阳极端稍稍倾向轴线,电子束掠射到荧光板上,显示出电子束的径迹,现在用该装置研究磁场对运动电荷的作用的实验,下列对该实验的说法正确的是( )
A.没有施加磁场时,电子束的径迹是一条抛物线
B.若图中左侧是阴极射线管的阴极,加上图示的磁场,电子束会向上偏转
C.施加磁场后,根据电子束在磁场中运动径迹和磁场方向,可由相关知识判断出阴极射线管两个电极的极性
D.施加磁场后,结合阴极射线管的两个电极的极性和电子束在磁场中运动的径迹,可以判断出磁场的方向,但无法判断出磁场的强弱
答案:C
解析:解答:A、没有施加磁场时,电子束只受电场离,在电场力作用下做加速直线运动,故A错误;
B、因为左边是阴极,右边是阳极,所以电子在阴极管中的运动方向是左到右,产生的电流方向是右到左(注意是电子带负电),根据左手定则,四指指向左,手掌对向N极(就是这个角度看过去指向纸面向里),此时大拇指指向下面,所以电子在洛伦兹力作用下轨迹向下偏转,故B错误;
C、根据轨迹和左手定则即可判断阴极射线管两个电极的极性,故C正确;
D、施加磁场后,结合阴极射线管的两个电极的极性和电子束在磁场中运动的径迹,可以判断出磁场的方向,根据曲率半径可判断出磁场强弱,故D错误;
故选:C
分析:此题要求要了解电子射线管的构造和原理,阴极是发射电子的电极,电子在磁场中运动,受到洛伦兹力的作用而发生偏转.从而显示电子运动的径迹,偏转方向有左手定则判断;根据曲率半径可判断磁场强弱;
2.从阴极射线管发射出的一束电子,通过图示的磁场,以下四幅图中能正确描绘电子偏转情况的是( )
A.B.
C.D.
答案:B
解析:解答:如图,电子束从阴极(﹣极)射出,根据左手定则:伸开左手,磁感线穿过手心,四指指向电子运动的相反方向,拇指指向洛伦兹力方向,判断得知电子所受的洛伦兹力方向向下,则电子束向下偏转,故B正确.
故选:B
分析:电子从阴极射出,在磁场中受到洛伦兹力而发生偏转,根据左手定则判断洛伦兹力的方向,即可确定电子束偏转的方向.
3.关于阴极射线的本质,下列说法正确的是( )
A.阴极射线本质是氢原子B.阴极射线本质是电磁波
C.阴极射线本质是电子D.阴极射线本质是X射线
答案:C
解析:解答:阴极射线是电子流,电子带负电.故ABD错误,C正确.
故选:C.
分析:首先知道阴极射线的实质是电子流,电子的电量与氢离子的电量相等,即可求解.
4.如图所示,甲、乙是分别用“阴极射线管”和“洛伦兹力演示仪”实验时的两幅图片,忽略地磁场的影响,下列说法正确的是( )
A.甲图中的电子束径迹是抛物线
B.乙图中的电子束径迹是圆形
C.甲图中的电子只受电场力作用
D.乙图中的电子受到的洛伦兹力是恒力
答案:B
解析:解答:A、如图,电子在洛伦兹力作用下,做匀速圆周运动.故A错误.
B、乙图中的电子束在磁场中,受到洛伦兹力作用,做匀速圆周运动,其径迹是圆形.故B正确,C错误.
D、洛伦兹力方向总是与电子速度方向垂直.故D错误.
故选:B.
分析:电子在磁场中受到洛伦兹力作用做匀速圆周运动.洛伦兹力方向总是与电子速度方向垂直,不做功.
5.如图所示的阴极射线管,无偏转电场时,电子束加速后打到荧屏中央形成亮斑.如果只逐渐增大M1M2之间的电势差,则( )
A.在荧屏上的亮斑向下移动B.在荧屏上的亮斑向下移动
C.偏转电场对电子做的功增大D.偏转电场的电场强度减小
答案:C
解析:解答:A、B、设电子由加速电场加速后的速度为v.电子在加速电场中运动过程,由动能定理得:
eU1=
解得,v=.
电子进入偏转电场后做匀变速曲线运动,沿极板方向做匀速直线运动,沿电场线方向做初速度为零的匀加速直线运动,则有:
水平方向有:L=vt
竖直方向有:a=
v=at
电子刚离开偏转电场时的偏转角正切为:tanα=
由以上各式解得:电子刚离开偏转电场时偏转角的正切为:tanα=,
则α=arctan.
即电子离开偏转电场时的偏转角α随偏转电压的增大而增大.如果只逐渐增大M1M2之间的电势差U2,在荧屏上的亮斑向上移动.故A不正确,B错误;
C、电子离开偏转电场时的偏转量:y==,
如果只逐渐增大M1M2之间的电势差U2,电子离开偏转电场时的偏转量将增大.
偏转电场对电子做的功:W=e E y,偏转量越大,电场力做的功越多.故C正确;
D、偏转电场的电场强度:E=,所以如果只逐渐增大M1M2之间的电势差U2,偏转电场的电场强度增大.故D错误.
故选:C
分析:电子在加速电场中运动时,电场力做正功,电子获得速度,根据动能定理求解电子离开加速电场后的速度;
电子垂直进入偏转电场后做类平抛运动,平行于极板方向做匀速直线运动,垂直于极板方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式求得偏转量的表达式与电场力做功的表达式,即可进行说明.
6.下列说法正确的是( )
A.阴极射线和β射线本质上都是电子流,都来自于原子的核外电子
B.温度越高,黑体辐射强度的极大值向频率较小的方向移动
C.天然放射现象的发现,让人们知道原子核是组成物质的最小微粒
D.公安机关对2014年5月初南京丢失铱﹣192放射源的4名责任人采取强制措施是因为该放射源放出大剂量的射线会污染环境和危害生命.
答案:D
解析:解答:A、阴极射线和β射线本质上都是电子流,阴极射线来自原子的核外电子,而β射线是由原子核中中子转化而来的,故A错误.
B、温度越高,黑体辐射强度的极大值向频率较大的方向移动;故B错误.
C、天然放射现象的发现,让人们知道原子核具有复杂结构,不是组成物质的最小微粒.故C不正确.
D、放射源放出大剂量的射线会污染环境和危害生命;故D正确.
故选:D
分析:β粒子来源于原子核中中子的转化;温度越高,黑体辐射强度的极大值向频率较大的方向移动;天然放射现象的发现,让人们知道原子核不是组成物质的最小微粒;放射源放出大剂量的射线会污染环境和危害生命;在光电效应现象中,光电流的饱和值会随着光照强度的增大而增大.
7.如图所示,阴极射线示波管的聚集电场是由电极A1、A2形成,实线为电场线,虚线为等势线,z轴为该电场的中心轴线,P、Q、R为一个从左侧进入聚焦电场的电子运动轨迹上的三点,则下列说法不正确的是( )
A.电极A1的电势低于电极A2的电势
B.电子在P点处的动能大于在Q点处的动能
C.电场中Q点的电场强度大于R点的电场强度
D.电子从P至R的运动过程中,电场力对它一直做正功
答案:D
解析:解答:A、沿电场线电势降低,因此电极A1的电势低于电极A2,故A错误;
B、电子从P至R的运动过程中,是由低电势向高电势运动时,电场力做正功,动能增加,电势能减小,故B错误,D正确;
C、等势线密的地方电场线也密,因此Q点电场线比R点电场线密,故Q点的电场强度大于R点的电场强度,因此C错误,
故选:D.
分析:沿电场线电势降低,电场强度的大小与电场线的疏密的关系;明确电子在电场中的受力特点以及电场力做功情况,从而进一步判断电势能、动能等变化情况.
8.如图为电视机显像管中电子束偏转的示意图.磁环上的偏转线圈通以图示方向的电流时,沿轴线向纸内射入的电子束的偏转方向( )
A.向上B.向左C.向下D.向右
答案:B
解析:解答:磁环上的偏转线圈通以图示方向的电流时,根据安培定则,在磁环上形成的磁场方向竖直向下,磁场是闭合的,故在磁环中心处的磁场是竖直向上的,在根据左手定则,当电子束沿轴线向纸内射入时,电子束受到向左的洛伦兹力,故电子束的偏转方向向左.故B正确、ACD错误.
故选:B.
分析:将整个线圈当成左右两部分研究,因为绕向变化,结合安培定则判断出磁场方向,由左手定则分析判断电子束所受的洛伦兹力方向,即可判断偏转方向.
9.如图所示,阴极射线管接通电源后,电子束由阴极沿x轴正方向射出,在荧光板上会看到一条亮线.要使荧光板上的亮线向z轴负方向偏转,可采用的方法是( )
A.加一沿y轴负方向的磁场B.加一沿z轴正方向的磁场
C.加一沿y轴正方向的电场D.加一沿z轴负方向的电场
答案:A
解析:解答:A、若加一沿y轴负方向的磁场,根据左手定则,洛伦兹力方向沿z轴负方向,亮线向下偏转,故A正确;
B、若加一沿z轴正方向的磁场,根据左手定则,洛伦兹力方向沿y轴负方向,亮线向y轴负方向偏转,故B错误;
C、若加一沿y轴正方向的电场,电子受电场力作用向外,亮线向y轴负方向偏转,故C错误.
D、若加一沿z轴负方向的电场,电子受到的电场力沿z轴的正方向,亮线向上偏转,故D错误.
故选:A.
分析:电子射线由阴极沿x轴方向射出,形成的亮线沿z轴正方向偏转,说明电子受到的洛伦兹力方向向下,将四个选项逐一代入,根据左手定则判断分析,选择可行的磁场方向
10.阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
A.电极A1的电势高于电极A2的电势
B.电场中Q点的电场强度大于R点的电场强度
C.电子在R点处的动能大于在P点处的动能
D.若将一束带正电的粒子从左侧射入聚焦电场也一定被会聚焦
答案:C
解析:解答:A、根据电场线与等势线垂直,可知管轴上电场线方向向左.根据沿电场线电势降低,得知电极A1的电势低于电极A2,故A错误;
B、等差等势线密的地方电场线也密,因此Q点电场线比R点电场线疏,故Q点的电场强度小于R点的电场强度,故B错误;
C、电子从低电势向高电势运动时,电场力做正功,动能增加,所以电子在R点处的动能大于在P点处的动能,故C正确.
D、若将一束带正电的粒子从左侧射入聚焦电场,所受的电场力向外侧,不可能会聚,故D错误.
故选:C.
分析:沿电场线电势降低,电场强度的大小与电场线的疏密的关系;明确电子在电场中的受力特点以及电场力做功情况,从而进一步判断电势能、动能等变化情况.根据正粒子所受的电场力方向,判断能否会聚.
11.放射性同位素发出的射线在科研、医疗、生产等诸多方面得到了广泛的应用,下列有关放射线应用的说法中正确的有( )
A.放射线改变了布料的性质使其不再因摩擦而生电,因此达到消除有害静电的目的
B.利用γ射线的贯穿性可以为金属探伤,也能进行人体的透视
C.用放射线照射作物种子能使其DNA发生变异,其结果一定是成为更优秀的品种
D.用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的危害
答案:D
解析:解答:A、利用放射线消除有害静电是利用α射线的电离性,使空气分子电离成导体,将静电放出,故A错误;
B、利用γ射线的贯穿性可以为金属探伤,γ射线对人体细胞伤害太大,因此不能用来人体透视,故B错误;
C、DNA变异并不一定都是有益的,也有时发生变害的一面,故C错误;
D、γ射线对人体细胞伤害太大,在用于治疗肿瘤时要严格控制剂量,故D正确;
故选:D.
分析:α射线使空气分子电离成导体,将静电放出;变异并不一定都是有益的;γ射线对人体细胞伤害大.
12.下列关于电磁污染的说法,不正确的是( )
A.电磁污染主要是指电磁辐射
B.电磁辐射会干扰其他仪器的正常工作
C.电磁辐射对人体和动物都有危害
D.频率越高的电磁波,电磁辐射的危害就越小
答案:D
解析:解答:A、电磁污染主要是指各种电磁辐射;如手机、雷达等;故A正确;
B、电磁辐射会干扰其他仪器并能人和动物造成伤害;故BC正确;
D、频率越高的电磁波,电磁辐射的危害就越大;故D错误;
本题选错误的;故选:D.
分析:各种电器在工作中均会造成电磁辐射,从而对环境造成污染!频率越高,电磁辐射远严重.
13.用α粒子轰击时,得到,同时放出一种粒子,关于这种粒子,下列说法中正确的是( )
A.它来自于原子核
B.它能穿透几厘米厚的铅板
C.它垂直进入磁场中不发生偏转
D.它是一种频率很高的光子
答案:A
解析:解答:A、根据核反应过程中的质量数和电荷数守恒可知该未知粒子的质量数和电荷数都为1,即该未知粒子为质子,带正电;核反应是原子核的反应,故它来自于原子核,故A正确;
B、质子流不能穿透几厘米厚的铅板,只有γ射线可以穿透几厘米厚的铅板,故B错误;
C、它垂直进入磁场中,会做匀速圆周运动,故C错误;
D、根据核反应过程中的质量数和电荷数守恒可知该未知粒子的质量数和电荷数都为1,即该未知粒子为质子,带正电,故D错误;
故选A.
分析:根据核反应的质量数和电荷数守恒,判断出未知粒子的质量数和电荷数即可明确该未知粒子的性质.
14.下列应用中把放射性同位素不作为示踪原子的是( )
A.利用含有放射性碘131的油,检测地下输油管的漏油情况
B.把含有放射性元素的肥料施给农作物,利用探测器的测量,找出合理的施肥规律
C.利用射线探伤法检查金属中的砂眼和裂纹
D.给怀疑患有甲状腺的病人注射碘131,诊断甲状腺的器质性和功能性疾病
答案:C
解析:解答:A、利用含有放射性碘131的油,检测地下输油管的漏油情况,是利用碘131的放射性,即将碘131作为示踪原子,故A正确;
B、把含有放射性元素的肥料施给农作物,利用探测器的测量,找出合理的施肥规律,是示踪原子的运用,故B正确;
C、利用射线探伤法检查金属中的砂眼和裂纹,是利用γ射线穿透能力强,不是示踪原子的运用,故C错误;
D、给怀疑患有甲状腺的病人注射碘131,诊断甲状腺的器质性和功能性疾病,是将碘131作为示踪原子,故D正确;
故选:C.
分析:放射性同位素碘131能做示踪原子;γ射线穿透能力强,通常会用于工业探伤.
15. 2011年3月11日,日本大地震引发了福岛核电站核泄漏事故,下列关于核电站的说法正确的是( )
A.核电站利用核聚变反应时释放的能量进行发电
B.核电站利用海洋的潮汐能发电
C.核能是可再生能源
D.核泄漏释放的放射性物质发出的射线对人体是有危害的
答案:D
解析:解答:目前核电站均采用重核裂变进行进行的,故AB错误;
核能是利用重核裂变进行的,是不可再生资源,故C错误;
长时间接受核辐射会使正常细胞发生癌变,故D正确.
故选D.
分析:正确解答本题要了解核能的应用以及放射性的污染和防护,同时了解裂变和聚变的区别.
二.填空题
16.如图所示,电子射线管(A为其阴极),放在蹄形磁铁的N、S两极间(图中C为N极),射线管的A、B两极分别接在直流高压电源的负极和正极.此时,荧光屏上的电子束运动径迹 偏转(填“向上”“向下”或“不”).
答案:向下
解析:解答:据题因为A是阴极,B是阳极,所以电子在阴极管中的运动方向是A到B,产生的电流方向是B到A(注意是电子带负电),根据左手定则,四指由B指向A,掌心对着N极此时拇指向下,所以电子束所受的洛伦兹力向下,轨迹向下偏转.
故答案为:向下
分析:此题要求要了解电子射线管的构造和原理.阴极是发射电子的电极,要接到高压的负极上,电子在磁场中运动,受到洛伦兹力的作用而发生偏转.从而显示电子运动的径迹,偏转方向有左手定则判断.
17.如图所示,把一电子射线管放在蹄形磁铁的两极之间,当电子由“﹣”,极射向“+”极时,将向 方偏转(填“上”或“下”).
答案:下
解析:解答:电子从阴极射向阳极,根据左手定则,磁感线穿入手心,四指指向电子运动的反方向,洛伦兹力的方向向下,则电子束向下偏转.
故答案为:下.
分析:阴极射线管电子从阴极射向阳极,运用左手定则判断电子束受到的洛伦兹力的方向,来判断电子束偏转的方向.
18.如图所示,电子枪射出的电子束进入示波管,在示波管正下方有竖直放置的通电环形导线,则示波管中的电子束将 偏转.(填“向上”“向下”“向里”“向外”)
答案:向上
解析:解答:由安培定则可知,在示波管下方环形电流的磁场在环形区域内磁感线方向垂直纸面向里,根据磁感线是闭合的曲线可知,在环形电流外侧磁感线方向垂直纸面向外;
电子束由左向右运动,电子束形成的电流方向水平向左,
由左手定则可知,电子束受到的安培力竖直向上,则电子束向上偏转;
故答案为:向上.
分析:由安培定则判断出环形导线中的电流在示波管位置的磁场方向;然后由左手定则判断出电子束受到的安培力方向,最后根据电子束的受力方向判断电子束如何偏转.
19.如图是阴极射线管的示意图.接通电源后,会有电子从阴极K射向阳极A,并在荧光屏上形成一条亮线.要使荧光屏上的亮线向下偏转,则可以加一个方向平行纸面 (填“向上”或“向下”)的电场,或者加一个方向垂直纸面 (填“向里”或“向外”)的磁场.
答案:向上|向里
解析:解答:由题意,根据正电荷受力与电场方向相同,若加一方向平行纸面向上的电场,电场力使得电子向下偏转.
若加一方向垂直纸面向里的磁场,根据左手定则,洛伦兹力方向竖直向下,亮线向下偏转.
故答案为:向上,向里.
分析:电子射线由阴极沿x轴方向射出,形成的亮线向下偏转,说明电子受到的洛伦兹力方向向下,根据左手定则判断分析,选择可行的磁场方向;或电子受到向下的电场力,从而确定电场强度的方向.
20.示波管应用了 (填“电场”或“磁场”)使电子束偏转的原理;纯电阻电路中,电动势为E,内电阻为r的电源的最大输出功率为 .
答案:电场|
解析:解答:示波管应用了电场使电子束偏转的原理.
根据数学知识分析可知,当外电阻等于电源的内电阻时,电源的输出功率最大,此时电路中电流为:I=,电源的最大输出输出功率为:Pm=I2R=I2r=.
故答案为:电场,.
分析:示波管应用了电场使电子束偏转的原理.当外电阻等于电源的内电阻时,电源的输出功率最大,由闭合电路欧姆定律和功率公式求出电源的最大的输出功率.
三.解答题
21.在电脑显示器的真空示波管内,控制电子束扫描的偏转场是匀强磁场,磁场区域是宽度为3.0cm的矩形,右边界距荧光屏20.0cm,高度足够.某段时间内磁场方向垂直纸面向外,磁感应强度B=4.55×10﹣3T不变.电子初速度不计,经U=4550V电压加速后沿中心线射入磁场,偏转后打在屏上产生亮点(若无磁场,亮点在屏中心),已知电子的质量m=0.91×10﹣30kg,电荷量e=1.6×10﹣19C.
(1)在图中大致图出电子运动的径迹;
答案:
(2)求亮点偏离荧光屏中心的距离.
答案:电子经U加速得到速度v0
由eU=
得v0==M/s=4×107m/s.
由evB=得①
R==0.05m=5cm②
sinα=0.6,cosα=0.8,tanα=0.75③
亮点偏离屏中心的距离:
y=(r﹣rcosα)+20.0tanα=5×(1-0.8)cm+20.0×cm=16cm;
解析:解答:(1)电子运动的径迹如图所示:
(2)电子经U加速得到速度v0
由eU=
得v0==M/s=4×107m/s.
由evB=得①
R==0.05m=5cm②
sinα=0.6,cosα=0.8,tanα=0.75③
亮点偏离屏中心的距离:
y=(r﹣rcosα)+20.0tanα=5×(1-0.8)cm+20.0×cm=16cm;
答:(1)在图中大致图出电子运动的径迹如图;(2)亮点偏离荧光屏中心的距离为16cm.
分析:(1)电子在电场中做直线运动,在磁场中由左手定则判断洛伦兹力方向向上,则电子向上偏转;(2)先由动能定理求出粒子离开电场时获得的速度,然后由牛顿第二定律求出粒子在磁场中圆周运动的半径,亮点偏离荧光屏中心的距离为磁场中竖直方向偏离的距离与做匀速直线运动过程竖直方向的位移之和.
22.汤姆孙测定电子比荷的实验装置如图甲所示.从阴极K发出的电子束经加速后,以相同速度沿水平中轴线射入极板D1、D2区域,射出后打在光屏上形成光点.在极板D1、D2区域内,若不加电场和磁场,电子将打在P1点;若只加偏转电压U,电子将打在P2点;若同时加上偏转电压U和一个方向垂直于纸面向外、磁感应强度大小为B的匀强磁场(图中未画出),电子又将打在P1点.已知极板长度为L,极板间距为d.忽略电子的重力及电子间的相互作用.
(1)求电子射人极板D1、D2区域时的速度大小;
答案:电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有:
evB=eE①
两极板间电场强度:E=②
解得:
v=③
(2)打在P2点的电子,相当于从D1、D2中轴线的中点O′射出,如图乙中的O′P2所示,已知∠P2O′P1=θ试推导出电子比荷的表达式;
答案:由几何关系得电子射出电场时竖直方向的侧移量:
y=tan8④
根据牛顿第二定律,有:=ma⑤
根据分位移公式,有:
L=vt⑥
y=⑦
又v=
联立各式得到:=⑧
(3)若两极板间只加题中所述的匀强磁场,电子在极板间的轨迹为一段圆弧,射出后打在P3点.测得圆弧半径为2L、P3与P1间距也为2L,求图乙中P1与P2点的间距a.
答案:如图所示,极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后做匀速直线运动,已知r=2L,由几何关系得到:α=30°⑨
射出磁场后水平方向的距离:
x==3L(10)
解得:
a=(+3L)tanθ=
解析:解答:(1)电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有:
evB=eE①
两极板间电场强度:E=②
解得:
v=③(2)由几何关系得电子射出电场时竖直方向的侧移量:
y=tan8④
根据牛顿第二定律,有:=ma⑤
根据分位移公式,有:
L=vt⑥
y=⑦
又v=
联立各式得到:=⑧(3)如图所示,极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后做匀速直线运动,已知r=2L,由几何关系得到:α=30°⑨
射出磁场后水平方向的距离:
x==3L(10)
解得:
a=(+3L)tanθ=
答:(1)电子射人极板D1、D2区域时的速度大小为;(2)电子比荷的表达式为为=;(3)图乙中P1与P2点的间距a为.
分析:(1)当电子在极板D1、D2间受到电场力与洛伦兹力平衡时,做匀速直线运动,受力平衡,由平衡条件可求出电子运动速度.(2)极板间仅有偏转电场时,电子在电场中做类平抛运动,将运动分解成沿电场强度方向与垂直电场强度方向的分运动,然后由牛顿第二定律和运动学公式列式后联立求解,从而可以求出电子比荷的表达式.(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,画出电子运动的轨迹,根据几何知识求解y.
23.在电子显像管内部,当未加偏转磁场时,电子枪打出的电子应沿直线运动打在荧光屏的正中心.但由于地磁场对带电粒子运动的影响,会出现在未加偏转磁场时电子束偏离直线运动的现象.已知电子质量为m=9.1×l0﹣31kg、元电荷e=1.6×l0﹣19C,从炽热灯丝发射出的电子(可视为初速度为零)经过加速电场加速动能是1.82×l04eV,沿水平方向由南向北运动.已知某地地磁场磁感应强度的竖直向下分量的大小为B=4.55×10﹣5T,地磁场对电子在加速过程中的影响可忽略不计.在未加偏转磁场的情况下,
(l)试判断电子束将偏向什么方向;
答案:根据左手定则,可以判断出电子束将偏向东方.
(2)求电子在该地磁场中运动的加速度的大小;
答案:设从加速电场射出的电子速度为v,据题有:Ek=,v==M/s=8×107m/s
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动,设电子的加速度为a,根据牛顿第二定律得:
evB=M
由以上各式解得:a==6.4×1014m/s2;
(3)若加速电场边缘到荧光屏的距离为l=40cm,试通过计算电子束的偏转位移说明该地磁场对电视画面有没有影响.(已知当|x|≤1时,=1-x)
答案:设电子在地磁场中运动的半径为R,
根据牛顿第二定律:evB=得R====10m
设电子在荧光屏上偏移的距离为x,根据图中的几何关系,有:
电子束的偏转位移d=R﹣=R-R=R[1﹣(1﹣ )]=R =10××M≈0.008m=8mm
所以该地磁场对电视画面有一定的影响,但不影响人们观看
解析:解答:(1)根据左手定则,可以判断出电子束将偏向东方.(2)设从加速电场射出的电子速度为v,据题有:Ek=,v==M/s=8×107m/s
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动,设电子的加速度为a,根据牛顿第二定律得:
evB=M
由以上各式解得:a==6.4×1014m/s2;(3)设电子在地磁场中运动的半径为R,
根据牛顿第二定律:evB=得R====10m
设电子在荧光屏上偏移的距离为x,根据图中的几何关系,有:
电子束的偏转位移d=R﹣=R-R=R[1﹣(1﹣ )]=R =10××M≈0.008m=8mm
所以该地磁场对电视画面有一定的影响,但不影响人们观看.
答:(1)电子束将偏向东偏;(2)电子在该地磁场中运动的加速度的大小为6.4×1014m/s2.(3)该地磁场对电视画面有一定的影响,但不影响人们观看.
分析:(1)电子在地磁场中受到洛伦兹力作用,根据左手定则判断出洛伦兹力的方向,即可知道电子束的偏转方向;(2)根据洛伦兹力等于向心力,列式求出电子在磁场中运动的加速度;(3)画出轨迹,根据几何知识求解打到荧光屏的电子与0点的距离.
24.汤姆孙测定电子比荷(电子的电荷量与质量之比)的实验装置如图所示.真空玻璃管内,阴极K发出的电子经加速后,穿过小孔A、C沿中心轴线OP1进入到两块水平正对放置的极板D1、D2间的区域,射出后到达右端的荧光屏上形成光点.若极板D1、D2间无电压,电子将打在荧光屏上的中心P1点;若在极板间施加偏转电压U,则电子将打P2点,P2与P1点的竖直间距为b,水平间距可忽略不计.若再在极板间施加一个方向垂直于纸面向外、磁感应强度为B的匀强磁场(图中未画出),则电子在荧光屏上产生的光点又回到P1点.已知极板的长度为L1,极板间的距离为d,极板右端到荧光屏间的距离为L2.忽略电子的重力及电子间的相互作用.
(1)求电子进入极板D1、D2间区域时速度的大小;
答案:电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有evB=eE
两极板间电场强度E=
解得v=
(2)推导出电子的比荷的表达式;
答案:极板间仅有偏转电场时,电子以速度v进入后,水平方向做匀速运动,在电场内的运动时间
电子在竖直方向做匀加速运动,设其加速度为a.
由牛顿第二定律有V=M
解得加速度a=
电子射出极板时竖直方向的偏转距离
电子射出极板时竖直方向的分速度为v=at1=
电子离开极板间电场后做匀速直线运动,经时间t2到达荧光屏,
电子在t2时间在竖直方向运动的距离y2=vyt2=
这样,电子在竖直方向上的总偏移距离b=y1+y2
解得电子比荷=
(3)若去掉极板D1、D2间的电压,只保留匀强磁场B,电子通过极板间的磁场区域的轨迹为一个半径为r的圆弧,阴极射线射出极板后落在荧光屏上的P3点.不计P3与P1点的水平间距,求P3与P1点的竖直间距y.
答案:极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,如答图所示.
则tan=
穿出磁场后在竖直方向上移动的距离y3=L2tan=
则y=r+y3-
解得y=r﹣
解析:解答:(1)电子在极板D1、D2间电场力与洛伦兹力的作用下沿中心轴线运动,即受力平衡,设电子的进入极板间时的速度为v.
由平衡条件有evB=eE
两极板间电场强度E=
解得v=(2)极板间仅有偏转电场时,电子以速度v进入后,水平方向做匀速运动,在电场内的运动时间
电子在竖直方向做匀加速运动,设其加速度为a.
由牛顿第二定律有V=M
解得加速度a=
电子射出极板时竖直方向的偏转距离
电子射出极板时竖直方向的分速度为v=at1=
电子离开极板间电场后做匀速直线运动,经时间t2到达荧光屏,
电子在t2时间在竖直方向运动的距离y2=vyt2=
这样,电子在竖直方向上的总偏移距离b=y1+y2
解得电子比荷=(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,如答图所示.
则tan=
穿出磁场后在竖直方向上移动的距离y3=L2tan=
则y=r+y3-
解得y=r﹣
答:(1)电子进入极板D1、D2间区域时速度的大小为;(2)电子的比荷的表达式为=;(3)P3与P1点的竖直间距y为r﹣.
分析:(1)当电子在极板D1、D2间受到电场力与洛伦兹力平衡时,做匀速直线运动,受力平衡,由平衡条件可求出电子运动速度.(2)极板间仅有偏转电场时,电子在电场中做类平抛运动,将运动分解成沿电场强度方向与垂直电场强度方向,然后由牛顿第二定律和运动学公式可求出偏转距离和离开电场时的速度.电子离开电场后,做匀速直线运动,从而可以求出偏转距离.(3)极板D1、D2间仅有匀强磁场时,电子做匀速圆周运动,射出磁场后电子做匀速直线运动,画出电子运动的轨迹,根据几何知识求解y.
25.电视机显像管简单原理如图所示,初速度不计的电子经加速电场加速后进入有限边界宽度为L的匀强磁场,磁感应强度为B,如要求电子束偏转角为α,已知电子电量为e,质量为m.
(1)画出整个过程的轨迹图;
答案:
(2)电子在磁场中运动的时间;
答案:根据电子做匀速圆周运动,则运动时间:t=
由T=
解得:t=;
(3)求加速电场的电势差U.
答案:电子经加速电场加速后,速度为v,
则由动能定理得:eU=mv2;
由几何关系得,电子运动半径:R=;
由牛顿第二定律,有:evB=;
由以上各式解得加速电压:U=
解析:解答:(1)电子现在加速电场中做匀加速直线运动,然后进入匀强磁场中作匀速圆周运动,轨迹如图;(2)根据电子做匀速圆周运动,则运动时间:t=
由T=
解得:t=;(3)电子经加速电场加速后,速度为v,
则由动能定理得:eU=mv2;
由几何关系得,电子运动半径:R=;
由牛顿第二定律,有:evB=;
由以上各式解得加速电压:U=;
答:(1)画出整个过程的轨迹图如上所示;(2)电子在磁场中运动的时间t=;(3)求加速电场的电势差U=.
分析:(1)根据电场力与洛伦兹力方向,结合力与运动的关系,从而即可求解;(2)根据电子的运动周期,结合圆心角,即可求解;(3)根据动能定理与牛顿第二定律,结合几何关系,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 23 页 (共 24 页) 版权所有@21世纪教育网
