期中测试卷(含答案)---2024-2025学年六年级数学下册(冀教版)
文档属性
| 名称 | 期中测试卷(含答案)---2024-2025学年六年级数学下册(冀教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级下册期中测试卷(冀教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.甲数的一半与乙数的相等(甲、乙两数都不为0),则甲数∶乙数=( )。
A.2∶ B.3∶4 C.4∶3 D.∶2
2. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
3.超市开展促销活动,有两种优惠方案。方案一:购物每满100元减60元,方案二:先打五折,然后在此基础上再打九折。小明要买一双340元的球鞋,( )。
A.方案一更省钱 B.方案二更省钱
C.两种方案省钱同样多 D.无法确定哪个更省钱
4.一根圆柱形木料长1.5m,把它截成3个大小完全一样的小圆柱,表面积增加了37.68dm2,这根木料的横截面积是( )dm2。
A.12.56 B.9.42 C.6.28
5.将一个底面直径为4厘米,高5厘米的圆柱切成两个完全相等的部分,( )切法表面积增加的大。
A. B.
6.出油率一定,香油的质量和芝麻的质量( )。
A.成正比例关系 B.成反比例关系 C.不成比例
7.小明睡觉时看了看墙上的温度计,温度是2℃, 早晨醒来后又看了看,发现下降了6℃,这时的温度是( )。
A.-2℃ B.-4℃ C.-6℃
8.大楼高60m,大楼模型高与实际高度比是1:400,大楼模型高( )。
A.15cm B.24cm C.12cm
9.已知2:3=6:9,如果将比例中的6改为9,那么9应改为( )。
A.4.5 B.6 C.12 D.13.5
10.下面每组中的四个数,不能组成比例的是( )。
A.2,0.25,3,0.375 B.18,8,5.4,245452
C. , , , D.30,25,6,125
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.在一个比例中,外项积不一定等于内项积。( )
12.满减促销和打折是一回事,例如:满100元减30元,实际上就是打七折。( )
13.右图中图形A绕点O旋转180°后就可以得到图形B。 ( )
14.如果a× =b× ,则a:b=16:9。( )
15.求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.m和n是两个非零的自然数,5m=4n,那么n:m= ∶ ;m比n少 %
17.一个比例的各项都是整数,它的两个比的比值都是,且第二项比第一项大6,第三项是第一项的3倍,这个比例是 。
18.等底等高的一个圆柱和一个圆锥,体积的和是72d㎡,圆柱的体积是 dm3,圆锥的体积是 dm3。
19.推门是 现象,缆车运动是 现象,剪中国结是 现象。(选填“平移”“旋转”或“轴对称”)
20. 是(线段)比例尺,表示图上1cm相当于实际距离 ,转化成数值比例尺是 。如果AB两地相距560千米,地图上相距 厘米。
21.在-6、3、0、-18、+7中, 是正数, 是负数, 既不是正数,也不是负数。
22.一个圆锥的体积是9.42立方分米,底面半径是3分米,它的高是 分米,和它等底等高的圆柱的体积是 立方分米。
23.有240人去春游,带队老师想准备一些饮料,商店“优惠告示”写着本店饮料6只空瓶可换1瓶饮料,240人至少买 瓶饮料,就能保证每人都喝一瓶。
24.在比例尺是1:500000的地图上,量得甲、乙两地的距离约为12厘米,两地之间的实际距离大约是 千米。
25.圆柱的高一定,圆柱的体积和底面积成 比例;圆柱的侧面积一定,底面周长和高成 比例。
阅卷人 四、计算题(23分)
得分
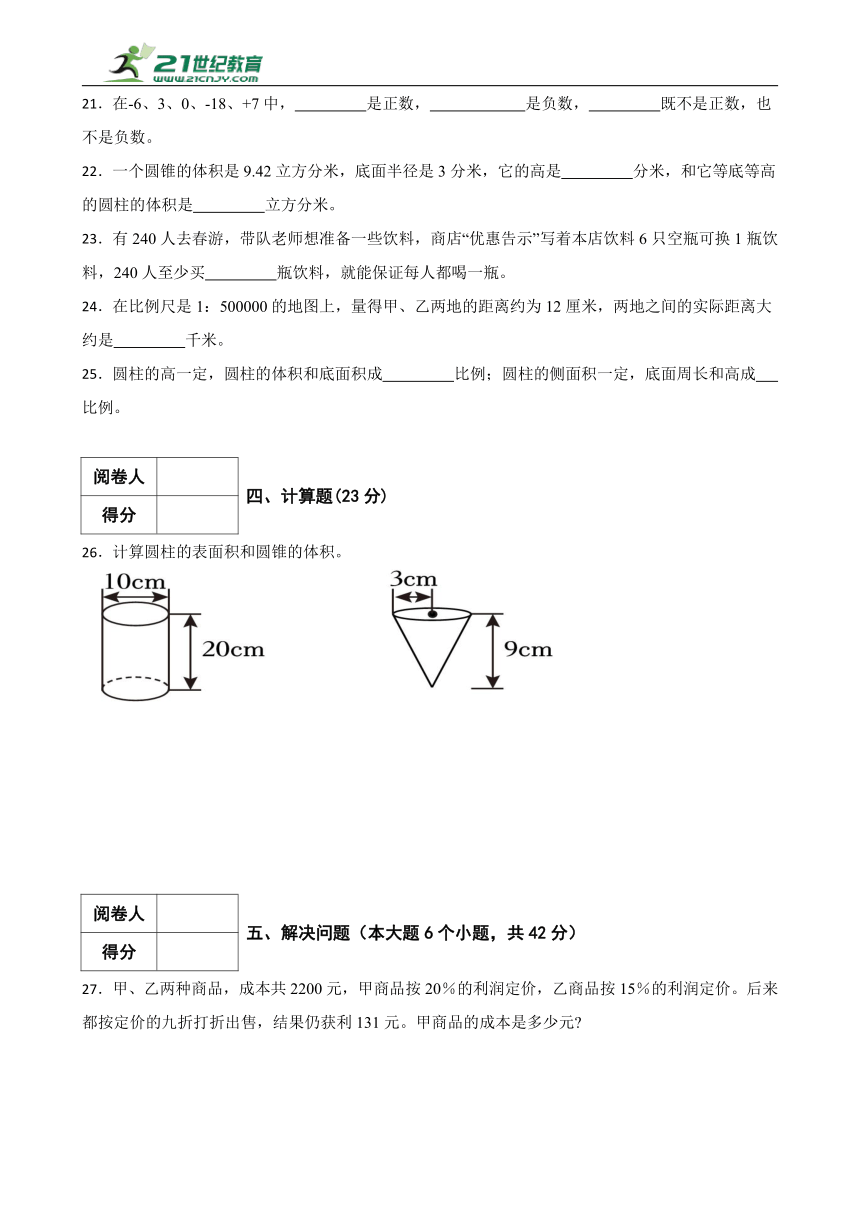
26.计算圆柱的表面积和圆锥的体积。
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
27.甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价。后来都按定价的九折打折出售,结果仍获利131元。甲商品的成本是多少元
28.一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水。(如图①,单位:cm,玻璃的厚度忽略不计)
(1)容器中水的体积是多少立方厘米?
(2)如果将这个容器倒过来(如图②),那么水面到圆锥顶点的高度是多少厘米?
29.小明调制了两杯蜂蜜水。第一杯用了30毫升蜂蜜和360毫升水。第二杯用了500毫升水,按照第一杯蜂蜜水中蜂蜜和水体积的比计算,第二杯应加入蜂蜜多少毫升?
30.一个近似圆锥形的碎石堆,底面周长12.56米,高0.6米。如果每立方米碎石大约重2吨,这堆碎石大约重多少吨?
31.将一根长16分米的圆柱形钢材截成三段较短的圆柱形,其表面积增加了24平方分米,这根钢材原来的体积是多少?
32.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为6cm,高为10 cm的圆锥形铁块(如右图)。
(1)这个铁块的体积是多少?
(2)如果把铁块从水中取出,那么容器中的水面高度将下降多少cm?
答案解析部分
1.C
解:甲数×=乙数×
甲数:乙数=:
甲数:乙数=4:3
故答案为:C。
由甲数的一半与乙数的可得:甲数×=乙数×,然后根据比例的基本性质(内项积=外项积),得到比例形式甲数:乙数=:,最后将:进行化简即可。
2.A
解:3÷0.75=4。
故答案为:A。
另一个外项=两个内项积÷一个外项。
3.B
解:340÷100=3(个)······40(元)
340-60×3
=340-180
=160(元);
340×50%×90%
=170×90%
=153(元)
160>153。
故答案为:B。
方案一的价钱=原价-减免的钱数,方案二的价钱=原价×折扣×折扣,然后再比较大小。
4.B
37.68÷4=9.42(dm2)
故答案为:B。
把一根圆柱形木料截成3个大小完全一样的小圆柱,表面积增加了4个横截面积,表面积增加的部分÷4=这根木料的横截面积,据此列式解答。
5.B
解:横切:3.14×(4÷2) ×2
=3.14×2 ×2
=3.14×4×2
=12.56×2
=25.12(平方厘米)
纵切:5×4×2
=20×2
=40(平方厘米)
40平方厘米>25.12平方厘米
故答案为:B。
(1)横切成两个圆柱,表面积增加了两个底面的面积,两个底面积=πr ×2;
(2)沿直径方向切成两个半圆,增加了两个长方形的面积,两个长方形的面积=圆柱的高×直径×2,然后比较大小即可。
6.A
解:出油率一定,香油的质量和芝麻的质量成正比例关系。
故答案为:A。
香油的质量÷芝麻的质量=出油率,所以出油率一定,香油的质量和芝麻的质量成正比例关系。
7.B
解:2-6=-4℃,所以这时的温度=-4℃。
故答案为:B。
这时的温度=睡觉时的温度-下降的温度,据此代入数据作答即可。
8.A
解:60×=0.15m=15cm,所以大楼模型高15cm。
故答案为:A。
大楼模型的高度=大楼的实际高度×比例尺,然后将单位进行换算,即1m=100cm。
9.D
已知2:3=6:9,如果将比例中的6改为9,那么9应改为13.5 。
故答案为:D。
在比例里,两外项之积等于两内项之积,将比例中的6改为9,一个内项扩大了9÷6=1.5倍,则外项也要扩大1.5倍,据此解答。
10.B
选项A,因为0.25×3=0.75,2×0.375=0.75,0.75=0.75,所以2,0.25,3,0.375能组成比例;
选项B,因为18×8=144,5.4×245452=1325440.8,144≠1325440.8,所以18,8,5.4,245452不能组成比例;
选项C,因为×=,×=,=,所以,,,能组成比例;
选项D,因为125×6=750,30×25=750,750=750,所以30,25,6,125能组成比例。
故答案为:B。
判断4个数能否组成比例的方法是:最大的数和最小的数相乘的积等于中间两个数字相乘的积,那么这四个数能组成比例,据此解答。
11.错误
解:比例的外项积一定等于内项积
故答案为:错误。
根据比例的基本性质( 在一个比例中,两个外项的积等于两个内项的积 )进行判断即可。
12.错误
解:①当原价是50元时,不能参与满100元减30元,
打七折,售价是50×70%=35(元),35<50,所以打七折更优惠;
②当原价是100元时,参与满100元减300元,售价是100-30=70(元),
打七折,售价是100×70%=70(元),70=70,满100减30元相当于打七折;
综上所述,原题说法错误;
故答案为:错误。
满100元减30元,也就是当原价满100元时,售价=原价-30;打七折,是把原价看作单位“1”,售价=原价×70%;据此判断。
13.错误
解:图中图形A绕点O旋转180°后不能得到图形B。
故答案为:错误。
如图所示,图形A绕点O旋转180°后得到的B如下图所示。
14.正确
解:a×=b×,所以a:b=:=16:9。
故答案为:正确。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
15.正确
解:求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。
故答案为:正确。
圆柱形铁皮通风管没有两个地面,只有侧面,所以求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。
16.5;4;20
解:5m=4n
n:m=5:4
(5-4)÷5×100%
=1÷5×100%
=0.2×100%
=20%
故答案为:5,4,20。
已知5m=4n,由比例的基本性质(内项积=外项积)得出n:m=5:4;用m比n少的值1除以n的值5再乘以100%,所得到的值即m比n少的百分比。
17.8∶14=24∶42
解:设第一项为x,第二项为x+6,第三项为3x
7x=4(x+6)
7x=4x+24
3x=24
x=8
x+6=8+6=14
3x=3×8=24
24÷=42
故答案为:8:14=24:42。
分析题干,已知前三项的关系,故假设第一项为x,则第二项为x+6,第三项为3x,又已知两个比的比值都是,故可得出第一项与第二项的比为,即,根据比例的基本性质(内项积=外项积),解出x的值为8,即第一项为8,进而得出第二项为14,第三项为24;已知第三项的值和比值,求第四项,24:第四项=,故第四项=24÷=42。
18.54;18
解:72÷4=18(立方分米)
18×3=54(立方分米)。
故答案为:54;18。
等底等高的圆柱的体积是圆锥体积的3倍,这个圆锥的体积=圆柱的体积÷(3+1),圆柱的体积=圆锥的体积×3。
19.旋转;平移;轴对称
解:推门是旋转现象,缆车运动是平移现象,剪中国结是轴对称现象。
故答案为:旋转;平移;轴对称。
旋转现象是图形或物体围绕某一点或轴进行圆周运动;
平移是指同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动;
轴对称是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
20.80km;1:8000000;7
解:线段比例尺表示图上1cm相当于实际距离80km;80km=8000000cm,所以转化成数值比例尺是1:8000000。如果AB两地相距560千米,560千米=56000000厘米,56000000×=7厘米,所以地图上相距7厘米。
故答案为:80km;1:8000000;7。
比例尺=图上距离:实际距离,其中比例尺中的前项和后项的单位要一致;
AB两地的图上距离=AB两地的实际距离÷比例尺,这里需要把AB两地的实际距离的单位进行换算,即1千米=100000厘米。
21.3、+7;-6、-18;0
解:这些数中,3、+7是正数,-6、-18是负数,0既不是正数,也不是负数。
故答案为:3、+7;-6、-18;0。
正数是大于0的数,正数前面的“+”可以不写;
负数是小于0的数,负数前面有“-”;
0既不是正数,也不是负数。
22.1;28.26
解:3.14×32
=3.14×9
=28.26(平方分米)
9.42÷÷28.26
=28.26÷28.26
=1(分米)
9.42×3=28.26(立方分米)。
故答案为:1;28.26。
圆锥的高=体积÷÷底面积;其中,底面积=π×半径2;和圆锥等底等高的圆柱的体积=圆锥的体积×3。
23.201
解:240÷7=34...2,
34×6=204 (瓶) ,
花204瓶的钱,204÷6=34,34÷6=5...4,可喝到的瓶数为:204+34+5=243,剩余5+4=9个空瓶,可再换1瓶饮料,余3个空瓶;此法浪费;
花203瓶的钱,203÷6=33...5,(33+5)÷6=6...2,可喝到的瓶数为:203+33+6=242,剩余6+2=8个空瓶,可再换1瓶饮料,余2个空瓶;此法浪费;
花202瓶的钱,202÷6=33...4,(33+4)÷6=6...1,可喝到的瓶数为:202+33+6=241,剩余6+1=7个空瓶,可再换1瓶饮料,余1个空瓶;此法浪费;
花201瓶的钱,201÷6=33...3,(33+3)÷6=6,可喝到的瓶数为:201+33+6=240,剩余6个空瓶,可再换一瓶饮料,刚刚好;
花200瓶的钱,200÷6=33...2,(33+2)÷6=5...5,可喝到的瓶数为:200+33+5=238,剩余5+5=10个空瓶,可再换1瓶饮料,余4个空瓶,此时总共可以喝到239瓶饮料和4个空瓶子,不能保证每个人都喝1瓶;
答: 240人至少买201瓶就可以了.
6只空瓶可换一瓶饮料,就是说花6瓶的钱可以喝到7瓶饮料,还余出1个瓶子,凑够6个空瓶还可以再换1瓶饮料,就尽量的让剩余空瓶都利用.
24.60
解:12÷÷100000
=6000000÷100000
=60(千米)。
故答案为:60。
实际距离=图上距离÷比例尺;然后单位换算。
25.正;反
解:圆柱的体积÷底面积=高(一定),圆柱的体积和底面积成正比例;
圆柱的底面周长×高=侧面积(一定),圆柱的底面周长和高成反比例。
故答案为:正;反。
根据圆柱的体积公式和侧面积公式分别判断圆柱的体积和底面积、圆柱的底面周长和高的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例。
26.解:3.14×10×20+3.14×(10÷2)×(10÷2)×2
=31.4×20+3.14×5×5×2
=628+157
=785(平方厘米)
3.14×3×3×9÷3=84.78(立方厘米)
答:圆柱的表面积是785平方厘米,圆锥的体积是84.75立方厘米。
直径÷2=半径,π×半径的平方=圆柱的底面积;π×底面直径=底面周长,底面周长×高=圆柱的侧面积;圆柱的底面积×2+圆柱的侧面积=圆柱的表面积;π×底面半径的平方×高÷3=圆锥的体积。
27.解:设甲商品的成本是x元,则乙商品的成本就是(2200-x)元, 0.9×(1.2x+2530-1.15x)=2331 0.05x+2530=2331÷0.9 0.05x=2590-2530 x=60÷0.05 x=1200答:甲商品的成本是1200元.
设甲商品的成本是x元,则乙商品的成本就是(2200-x)元,等量关系:(甲的售价+乙的售价)×90%=总成本+131,根据等量关系列出方程,解方程求出甲商品的成本即可.
28.(1)解:8÷2=4(厘米)
3.14×42×6
=50.24×6
=301.44(立方厘米)
答:容器中水的体积是301.44立方厘米。
(2)解:301.44-50.24×6×
=301.44-100.48
=200.96(立方厘米)
200.96÷50.24+6
=4+6
=10(厘米)
答:水面到圆锥顶点的高度是10厘米。
(1)容器中水的体积=π×半径2×高,半径=直径÷2;
(2)水面到圆锥顶点的高度=圆柱的高+圆锥的高,其中,圆柱的高=6厘米,圆锥的高=(水的体积-圆锥的底面积×高×)÷底面积。
29.解:设第二杯应加入蜂蜜x毫升。
30:360=x:500
360x=30×500
360x=15000
x=15000÷360
x≈41.7
答:第二杯应加入蜂蜜41.7毫升。
第一杯中蜂蜜质量:水的质量=第二杯中蜂蜜质量:水质量,据此列比例,然后根据比例的基本性质和等式性质解比例。
30.略
已知圆锥的底面周长C,可以求出圆锥的底面半径r,C÷π÷2=r;要求圆锥的体积,用公式:V=πr2h,据此列式计算,然后用每立方米碎石的质量×碎石堆的体积=这堆碎石的质量,据此列式解答。
31.解:圆柱的底面积:24÷4=6(平方分米)
圆柱的体积:6×16=96(立方分米)
答:这根钢材的体积是96立方分米.
由题意可知:一根16分米长的圆柱形钢材,锯成3段后,增加了4个面,增加的面积已知,从而可以求出1个面的面积,也就是钢材的底面积,进而利用圆锥的体积公式就可以求出圆柱形钢材的体积.
32.(1)解:6÷2=3(cm)
3.14×32×10×
=3.14×(9×)×10
=3.14×3×10
=9.42×10
=94.2(cm3)
答:这个铁块的体积是94.2cm3。
(2)解:10÷2=5(cm)
94.2÷3.14÷52
=30÷25
=1.2(cm)
答:容器中的水面高度将下降1.2cm。
(1)这个铁块的体积=圆锥的体积=π×半径2×高×;
(2)容器中水面下降的高度=圆锥的体积÷圆柱的底面积;其中,圆柱的底面积=π×半径2。
2024-2025学年六年级下册期中测试卷(冀教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.甲数的一半与乙数的相等(甲、乙两数都不为0),则甲数∶乙数=( )。
A.2∶ B.3∶4 C.4∶3 D.∶2
2. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
3.超市开展促销活动,有两种优惠方案。方案一:购物每满100元减60元,方案二:先打五折,然后在此基础上再打九折。小明要买一双340元的球鞋,( )。
A.方案一更省钱 B.方案二更省钱
C.两种方案省钱同样多 D.无法确定哪个更省钱
4.一根圆柱形木料长1.5m,把它截成3个大小完全一样的小圆柱,表面积增加了37.68dm2,这根木料的横截面积是( )dm2。
A.12.56 B.9.42 C.6.28
5.将一个底面直径为4厘米,高5厘米的圆柱切成两个完全相等的部分,( )切法表面积增加的大。
A. B.
6.出油率一定,香油的质量和芝麻的质量( )。
A.成正比例关系 B.成反比例关系 C.不成比例
7.小明睡觉时看了看墙上的温度计,温度是2℃, 早晨醒来后又看了看,发现下降了6℃,这时的温度是( )。
A.-2℃ B.-4℃ C.-6℃
8.大楼高60m,大楼模型高与实际高度比是1:400,大楼模型高( )。
A.15cm B.24cm C.12cm
9.已知2:3=6:9,如果将比例中的6改为9,那么9应改为( )。
A.4.5 B.6 C.12 D.13.5
10.下面每组中的四个数,不能组成比例的是( )。
A.2,0.25,3,0.375 B.18,8,5.4,245452
C. , , , D.30,25,6,125
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.在一个比例中,外项积不一定等于内项积。( )
12.满减促销和打折是一回事,例如:满100元减30元,实际上就是打七折。( )
13.右图中图形A绕点O旋转180°后就可以得到图形B。 ( )
14.如果a× =b× ,则a:b=16:9。( )
15.求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.m和n是两个非零的自然数,5m=4n,那么n:m= ∶ ;m比n少 %
17.一个比例的各项都是整数,它的两个比的比值都是,且第二项比第一项大6,第三项是第一项的3倍,这个比例是 。
18.等底等高的一个圆柱和一个圆锥,体积的和是72d㎡,圆柱的体积是 dm3,圆锥的体积是 dm3。
19.推门是 现象,缆车运动是 现象,剪中国结是 现象。(选填“平移”“旋转”或“轴对称”)
20. 是(线段)比例尺,表示图上1cm相当于实际距离 ,转化成数值比例尺是 。如果AB两地相距560千米,地图上相距 厘米。
21.在-6、3、0、-18、+7中, 是正数, 是负数, 既不是正数,也不是负数。
22.一个圆锥的体积是9.42立方分米,底面半径是3分米,它的高是 分米,和它等底等高的圆柱的体积是 立方分米。
23.有240人去春游,带队老师想准备一些饮料,商店“优惠告示”写着本店饮料6只空瓶可换1瓶饮料,240人至少买 瓶饮料,就能保证每人都喝一瓶。
24.在比例尺是1:500000的地图上,量得甲、乙两地的距离约为12厘米,两地之间的实际距离大约是 千米。
25.圆柱的高一定,圆柱的体积和底面积成 比例;圆柱的侧面积一定,底面周长和高成 比例。
阅卷人 四、计算题(23分)
得分
26.计算圆柱的表面积和圆锥的体积。
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
27.甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价。后来都按定价的九折打折出售,结果仍获利131元。甲商品的成本是多少元
28.一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水。(如图①,单位:cm,玻璃的厚度忽略不计)
(1)容器中水的体积是多少立方厘米?
(2)如果将这个容器倒过来(如图②),那么水面到圆锥顶点的高度是多少厘米?
29.小明调制了两杯蜂蜜水。第一杯用了30毫升蜂蜜和360毫升水。第二杯用了500毫升水,按照第一杯蜂蜜水中蜂蜜和水体积的比计算,第二杯应加入蜂蜜多少毫升?
30.一个近似圆锥形的碎石堆,底面周长12.56米,高0.6米。如果每立方米碎石大约重2吨,这堆碎石大约重多少吨?
31.将一根长16分米的圆柱形钢材截成三段较短的圆柱形,其表面积增加了24平方分米,这根钢材原来的体积是多少?
32.一个圆柱形玻璃容器里装有水,水中浸没着一个底面直径为6cm,高为10 cm的圆锥形铁块(如右图)。
(1)这个铁块的体积是多少?
(2)如果把铁块从水中取出,那么容器中的水面高度将下降多少cm?
答案解析部分
1.C
解:甲数×=乙数×
甲数:乙数=:
甲数:乙数=4:3
故答案为:C。
由甲数的一半与乙数的可得:甲数×=乙数×,然后根据比例的基本性质(内项积=外项积),得到比例形式甲数:乙数=:,最后将:进行化简即可。
2.A
解:3÷0.75=4。
故答案为:A。
另一个外项=两个内项积÷一个外项。
3.B
解:340÷100=3(个)······40(元)
340-60×3
=340-180
=160(元);
340×50%×90%
=170×90%
=153(元)
160>153。
故答案为:B。
方案一的价钱=原价-减免的钱数,方案二的价钱=原价×折扣×折扣,然后再比较大小。
4.B
37.68÷4=9.42(dm2)
故答案为:B。
把一根圆柱形木料截成3个大小完全一样的小圆柱,表面积增加了4个横截面积,表面积增加的部分÷4=这根木料的横截面积,据此列式解答。
5.B
解:横切:3.14×(4÷2) ×2
=3.14×2 ×2
=3.14×4×2
=12.56×2
=25.12(平方厘米)
纵切:5×4×2
=20×2
=40(平方厘米)
40平方厘米>25.12平方厘米
故答案为:B。
(1)横切成两个圆柱,表面积增加了两个底面的面积,两个底面积=πr ×2;
(2)沿直径方向切成两个半圆,增加了两个长方形的面积,两个长方形的面积=圆柱的高×直径×2,然后比较大小即可。
6.A
解:出油率一定,香油的质量和芝麻的质量成正比例关系。
故答案为:A。
香油的质量÷芝麻的质量=出油率,所以出油率一定,香油的质量和芝麻的质量成正比例关系。
7.B
解:2-6=-4℃,所以这时的温度=-4℃。
故答案为:B。
这时的温度=睡觉时的温度-下降的温度,据此代入数据作答即可。
8.A
解:60×=0.15m=15cm,所以大楼模型高15cm。
故答案为:A。
大楼模型的高度=大楼的实际高度×比例尺,然后将单位进行换算,即1m=100cm。
9.D
已知2:3=6:9,如果将比例中的6改为9,那么9应改为13.5 。
故答案为:D。
在比例里,两外项之积等于两内项之积,将比例中的6改为9,一个内项扩大了9÷6=1.5倍,则外项也要扩大1.5倍,据此解答。
10.B
选项A,因为0.25×3=0.75,2×0.375=0.75,0.75=0.75,所以2,0.25,3,0.375能组成比例;
选项B,因为18×8=144,5.4×245452=1325440.8,144≠1325440.8,所以18,8,5.4,245452不能组成比例;
选项C,因为×=,×=,=,所以,,,能组成比例;
选项D,因为125×6=750,30×25=750,750=750,所以30,25,6,125能组成比例。
故答案为:B。
判断4个数能否组成比例的方法是:最大的数和最小的数相乘的积等于中间两个数字相乘的积,那么这四个数能组成比例,据此解答。
11.错误
解:比例的外项积一定等于内项积
故答案为:错误。
根据比例的基本性质( 在一个比例中,两个外项的积等于两个内项的积 )进行判断即可。
12.错误
解:①当原价是50元时,不能参与满100元减30元,
打七折,售价是50×70%=35(元),35<50,所以打七折更优惠;
②当原价是100元时,参与满100元减300元,售价是100-30=70(元),
打七折,售价是100×70%=70(元),70=70,满100减30元相当于打七折;
综上所述,原题说法错误;
故答案为:错误。
满100元减30元,也就是当原价满100元时,售价=原价-30;打七折,是把原价看作单位“1”,售价=原价×70%;据此判断。
13.错误
解:图中图形A绕点O旋转180°后不能得到图形B。
故答案为:错误。
如图所示,图形A绕点O旋转180°后得到的B如下图所示。
14.正确
解:a×=b×,所以a:b=:=16:9。
故答案为:正确。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
15.正确
解:求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。
故答案为:正确。
圆柱形铁皮通风管没有两个地面,只有侧面,所以求一节圆柱形铁皮通风管用铁皮多少平方米,就是求圆柱的侧面积。
16.5;4;20
解:5m=4n
n:m=5:4
(5-4)÷5×100%
=1÷5×100%
=0.2×100%
=20%
故答案为:5,4,20。
已知5m=4n,由比例的基本性质(内项积=外项积)得出n:m=5:4;用m比n少的值1除以n的值5再乘以100%,所得到的值即m比n少的百分比。
17.8∶14=24∶42
解:设第一项为x,第二项为x+6,第三项为3x
7x=4(x+6)
7x=4x+24
3x=24
x=8
x+6=8+6=14
3x=3×8=24
24÷=42
故答案为:8:14=24:42。
分析题干,已知前三项的关系,故假设第一项为x,则第二项为x+6,第三项为3x,又已知两个比的比值都是,故可得出第一项与第二项的比为,即,根据比例的基本性质(内项积=外项积),解出x的值为8,即第一项为8,进而得出第二项为14,第三项为24;已知第三项的值和比值,求第四项,24:第四项=,故第四项=24÷=42。
18.54;18
解:72÷4=18(立方分米)
18×3=54(立方分米)。
故答案为:54;18。
等底等高的圆柱的体积是圆锥体积的3倍,这个圆锥的体积=圆柱的体积÷(3+1),圆柱的体积=圆锥的体积×3。
19.旋转;平移;轴对称
解:推门是旋转现象,缆车运动是平移现象,剪中国结是轴对称现象。
故答案为:旋转;平移;轴对称。
旋转现象是图形或物体围绕某一点或轴进行圆周运动;
平移是指同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动;
轴对称是指平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
20.80km;1:8000000;7
解:线段比例尺表示图上1cm相当于实际距离80km;80km=8000000cm,所以转化成数值比例尺是1:8000000。如果AB两地相距560千米,560千米=56000000厘米,56000000×=7厘米,所以地图上相距7厘米。
故答案为:80km;1:8000000;7。
比例尺=图上距离:实际距离,其中比例尺中的前项和后项的单位要一致;
AB两地的图上距离=AB两地的实际距离÷比例尺,这里需要把AB两地的实际距离的单位进行换算,即1千米=100000厘米。
21.3、+7;-6、-18;0
解:这些数中,3、+7是正数,-6、-18是负数,0既不是正数,也不是负数。
故答案为:3、+7;-6、-18;0。
正数是大于0的数,正数前面的“+”可以不写;
负数是小于0的数,负数前面有“-”;
0既不是正数,也不是负数。
22.1;28.26
解:3.14×32
=3.14×9
=28.26(平方分米)
9.42÷÷28.26
=28.26÷28.26
=1(分米)
9.42×3=28.26(立方分米)。
故答案为:1;28.26。
圆锥的高=体积÷÷底面积;其中,底面积=π×半径2;和圆锥等底等高的圆柱的体积=圆锥的体积×3。
23.201
解:240÷7=34...2,
34×6=204 (瓶) ,
花204瓶的钱,204÷6=34,34÷6=5...4,可喝到的瓶数为:204+34+5=243,剩余5+4=9个空瓶,可再换1瓶饮料,余3个空瓶;此法浪费;
花203瓶的钱,203÷6=33...5,(33+5)÷6=6...2,可喝到的瓶数为:203+33+6=242,剩余6+2=8个空瓶,可再换1瓶饮料,余2个空瓶;此法浪费;
花202瓶的钱,202÷6=33...4,(33+4)÷6=6...1,可喝到的瓶数为:202+33+6=241,剩余6+1=7个空瓶,可再换1瓶饮料,余1个空瓶;此法浪费;
花201瓶的钱,201÷6=33...3,(33+3)÷6=6,可喝到的瓶数为:201+33+6=240,剩余6个空瓶,可再换一瓶饮料,刚刚好;
花200瓶的钱,200÷6=33...2,(33+2)÷6=5...5,可喝到的瓶数为:200+33+5=238,剩余5+5=10个空瓶,可再换1瓶饮料,余4个空瓶,此时总共可以喝到239瓶饮料和4个空瓶子,不能保证每个人都喝1瓶;
答: 240人至少买201瓶就可以了.
6只空瓶可换一瓶饮料,就是说花6瓶的钱可以喝到7瓶饮料,还余出1个瓶子,凑够6个空瓶还可以再换1瓶饮料,就尽量的让剩余空瓶都利用.
24.60
解:12÷÷100000
=6000000÷100000
=60(千米)。
故答案为:60。
实际距离=图上距离÷比例尺;然后单位换算。
25.正;反
解:圆柱的体积÷底面积=高(一定),圆柱的体积和底面积成正比例;
圆柱的底面周长×高=侧面积(一定),圆柱的底面周长和高成反比例。
故答案为:正;反。
根据圆柱的体积公式和侧面积公式分别判断圆柱的体积和底面积、圆柱的底面周长和高的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例。
26.解:3.14×10×20+3.14×(10÷2)×(10÷2)×2
=31.4×20+3.14×5×5×2
=628+157
=785(平方厘米)
3.14×3×3×9÷3=84.78(立方厘米)
答:圆柱的表面积是785平方厘米,圆锥的体积是84.75立方厘米。
直径÷2=半径,π×半径的平方=圆柱的底面积;π×底面直径=底面周长,底面周长×高=圆柱的侧面积;圆柱的底面积×2+圆柱的侧面积=圆柱的表面积;π×底面半径的平方×高÷3=圆锥的体积。
27.解:设甲商品的成本是x元,则乙商品的成本就是(2200-x)元, 0.9×(1.2x+2530-1.15x)=2331 0.05x+2530=2331÷0.9 0.05x=2590-2530 x=60÷0.05 x=1200答:甲商品的成本是1200元.
设甲商品的成本是x元,则乙商品的成本就是(2200-x)元,等量关系:(甲的售价+乙的售价)×90%=总成本+131,根据等量关系列出方程,解方程求出甲商品的成本即可.
28.(1)解:8÷2=4(厘米)
3.14×42×6
=50.24×6
=301.44(立方厘米)
答:容器中水的体积是301.44立方厘米。
(2)解:301.44-50.24×6×
=301.44-100.48
=200.96(立方厘米)
200.96÷50.24+6
=4+6
=10(厘米)
答:水面到圆锥顶点的高度是10厘米。
(1)容器中水的体积=π×半径2×高,半径=直径÷2;
(2)水面到圆锥顶点的高度=圆柱的高+圆锥的高,其中,圆柱的高=6厘米,圆锥的高=(水的体积-圆锥的底面积×高×)÷底面积。
29.解:设第二杯应加入蜂蜜x毫升。
30:360=x:500
360x=30×500
360x=15000
x=15000÷360
x≈41.7
答:第二杯应加入蜂蜜41.7毫升。
第一杯中蜂蜜质量:水的质量=第二杯中蜂蜜质量:水质量,据此列比例,然后根据比例的基本性质和等式性质解比例。
30.略
已知圆锥的底面周长C,可以求出圆锥的底面半径r,C÷π÷2=r;要求圆锥的体积,用公式:V=πr2h,据此列式计算,然后用每立方米碎石的质量×碎石堆的体积=这堆碎石的质量,据此列式解答。
31.解:圆柱的底面积:24÷4=6(平方分米)
圆柱的体积:6×16=96(立方分米)
答:这根钢材的体积是96立方分米.
由题意可知:一根16分米长的圆柱形钢材,锯成3段后,增加了4个面,增加的面积已知,从而可以求出1个面的面积,也就是钢材的底面积,进而利用圆锥的体积公式就可以求出圆柱形钢材的体积.
32.(1)解:6÷2=3(cm)
3.14×32×10×
=3.14×(9×)×10
=3.14×3×10
=9.42×10
=94.2(cm3)
答:这个铁块的体积是94.2cm3。
(2)解:10÷2=5(cm)
94.2÷3.14÷52
=30÷25
=1.2(cm)
答:容器中的水面高度将下降1.2cm。
(1)这个铁块的体积=圆锥的体积=π×半径2×高×;
(2)容器中水面下降的高度=圆锥的体积÷圆柱的底面积;其中,圆柱的底面积=π×半径2。
同课章节目录
