期中测试卷(含答案)---2024-2025学年六年级数学下册(人教版)
文档属性
| 名称 | 期中测试卷(含答案)---2024-2025学年六年级数学下册(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 07:44:37 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级下册期中测试卷(人教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.甲数的一半与乙数的相等(甲、乙两数都不为0),则甲数∶乙数=( )。
A.2∶ B.3∶4 C.4∶3 D.∶2
2. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
3.如图,圆柱形容器的底面半径为10cm,水的高度为12 cm,水中浸没着一个底面半径为4 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm。根据以上信息,不能解决的问题是( )。(容器的厚度忽略不计)
A.容器内装了多少水 B.铅锤的体积是多少
C.铅锤的高是多少 D.容器的高是多少
4.把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,( )。
A.面积扩大到原来的2倍 B.周长扩大到原来的2倍
C.面积扩大到原来的 D.周长缩小到原来的
5.图上距离一定时,比例尺与实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.一个圆柱的底面直径是10厘米,若高增加2厘米,则侧面积增加( )平方厘米。
A.3.14 B.31.4 C.62.8 D.6.28
7.学校今年的水电费比去年节约二成,表示今年的水电费是去年的( )。
A.20% B.120% C.80% D.12%
8.某服装店在进价的基础上提高两成后作为标价,照这样计算,一件进价420元的衣服应标价多少元?正确的列式是( )。
A.420×20% B.420×(1+20%)
C.420÷(1-20%) D.420×(1-20%)
9.图形 A 如何旋转得到图形C?下列选项中正确的是( )。
A.图形 A绕点O顺时针旋转 90°得到图形C
B.图形 A 绕点O 逆时针旋转 90°得到图形C
C.图形A绕点O 逆时针旋转 180°得到图形
D.再绕点O逆时针旋转 90°得到图形C
10.在比例尺是1:6000000的地图上,量得南京到北京的距离是15厘米,南京到北京的实际距离大约是( )
A.800千米 B.90千米 C.900千米 D.80千米
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.在一个比例中,外项积不一定等于内项积。( )
12.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
13.一幅地图的比例尺是1:1000000km。( )
14.圆柱的侧面展开图可以是长方形、平行四边形或梯形。( )
15.今天的气温比昨天下降了5℃,今天的最低气温是-5℃。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.用一张长4.5分米,宽1.2分米的长方形铁皮制成一个圆柱,这个圆柱的侧面积最多是 平方分米。(接口处不计)
17.一个比例的各项都是整数,它的两个比的比值都是,且第二项比第一项大6,第三项是第一项的3倍,这个比例是 。
18.一个圆柱底面半径和高都扩大为原来的3倍,侧面积就扩大为原来的 倍,体积就扩大为原来的 倍。
19.一个由两位数字组成的密码改为由两个大写字母组成的密码,密码总数增加 个。
20.一个圆柱的底面直径是10cm,高是20cm,将它的侧面沿高展开后得到一个长方形。这个长方形的长是 cm,宽是 cm。
21.潜水艇上浮50米,记作+50米,小下潜120米应记作 米。
22.=C(B不等于0)当A一定时,B和C成 比例,当C一定时,A和B成 比例。
23. 一个零件长7mm,画在设计图上是14cm,这幅设计图的比例尺是 。
24.甲数的等于乙数的(甲乙不等于0)甲数与乙数的最简比是 。
25.超市促销活动中所有商品一律八折,一件原价240元的衣服,现在买可以节省 元;王阿姨在促销活动中花400元购买了一套家电,原价 元。
阅卷人 四、计算题(23分)
得分
26.直接写出得数
10.4+ = ÷70%= 1÷10%= 0÷1%=
24×25%= 1-75%= 180%- = 2×80%=
27.解方程
(1)33%x=16.5
(2)x-25%x=12
(3)160%x+4.5×20%=8.9
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价。后来都按定价的九折打折出售,结果仍获利131元。甲商品的成本是多少元
29.在一幅比例尺是1∶300的地图上量得甲、乙两地相距18厘米,那么在另一幅比例尺为1∶200的地图上,这两地间的距离应是多少厘米?
30.底面直径是20厘米的圆柱形容器中装有一些水,将一个高是10厘米,底面直径是12厘米的圆锥形铅锤浸没入水中,取出铅锤时,水面下降多少?
31.如图,一个圆锥的底面半径是5cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积增加了60cm2.这个圆锥的体积是多少立方厘米?
32.打谷场有一个近似于圆锥形的小麦堆,测得底面周长是9.42m,高是1.2m,每立方米小麦约重750kg。这堆小麦大约重多少千克?(得数精确到整千克)
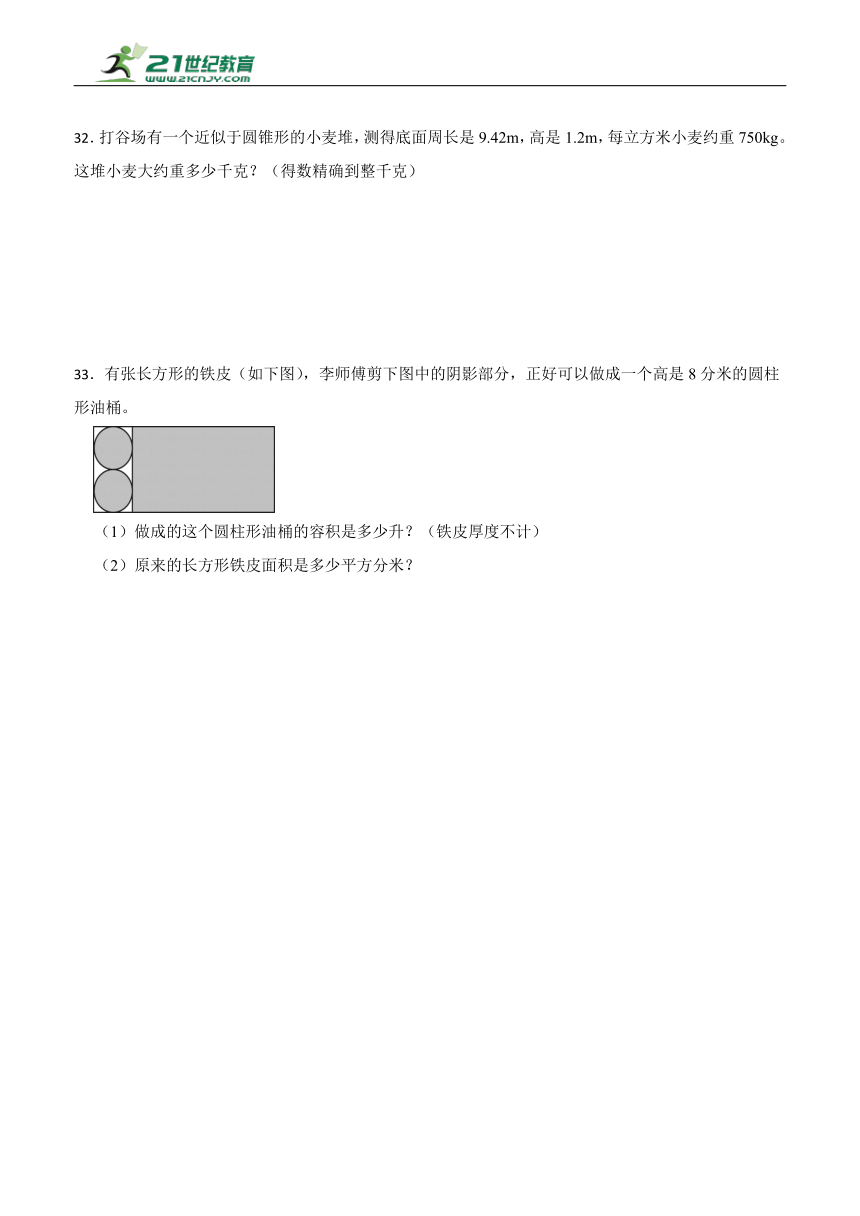
33.有张长方形的铁皮(如下图),李师傅剪下图中的阴影部分,正好可以做成一个高是8分米的圆柱形油桶。
(1)做成的这个圆柱形油桶的容积是多少升?(铁皮厚度不计)
(2)原来的长方形铁皮面积是多少平方分米?
答案解析部分
1.C
解:甲数×=乙数×
甲数:乙数=:
甲数:乙数=4:3
故答案为:C。
由甲数的一半与乙数的可得:甲数×=乙数×,然后根据比例的基本性质(内项积=外项积),得到比例形式甲数:乙数=:,最后将:进行化简即可。
2.A
解:3÷0.75=4。
故答案为:A。
另一个外项=两个内项积÷一个外项。
3.D
解:A项:已知圆柱形容器的底面半径和水的高度,用圆柱形容器的底面积乘水的高度,可求出容器内水的体积;
B项:把铅锤从水中取出后,水面下降了0.7cm,水面下降部分的体积即为铅锤的体积;
C项:已知铅锤的底面半径,可求出铅锤的底面积,进而求出铅锤的高;
D项:容器的高未知,容器的容积也未知,无法求出容器的高是多少厘米。
故答案为:D。
首先,题目给出圆柱容器的底面半径(10cm)、初始水高(12cm),以及取出圆锥铅锤后水面下降的高度(0.7cm)。通过这些信息,可以计算铅锤的体积,进而推导铅锤的高。同时,容器内原有水量可通过圆柱体积公式直接计算。但容器的总高度无法通过现有数据确定,因为题目未提供容器是否装满或铅锤取出后的水位高度与容器高度的关系,所以无法求出容器的高是多少厘米。
4.B
把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,周长扩大到原来的2倍.
故答案为:B.
把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,边长扩大了2倍,所以周长扩大到原来的2倍,面积扩大到原来的4倍,据此解答.
5.B
解:实际距离×比例尺=图上距离(一定),图上距离一定时,比例尺与实际距离成反比例。
故答案为:B。
实际距离×比例尺=图上距离(一定),乘积一定,比例尺与实际距离成反比例。
6.C
解:侧面积增加10×3.14×2=62.8平方厘米。
故答案为:C。
侧面积增加的面积=底面周长×高增加的长度,其中底面周长=底面直径×π。
7.C
解:1-20%=80%。
故答案为:C。
今年的水电费比去年节约二成,把去年的水电费看作单位“1”,即今年的水电费是去年水电费的(1-20%);据此解答。
8.B
解:标价是进价的(1+20%),已知进价,求标价,用乘法计算,列式是420×(1+20%)。
故答案为:B。
根据题意可知,标价是进价的(1+20%),已知进价,求标价,用乘法计算。
9.A
解:图形A绕点O逆时针旋转 90°得到图形C。
故答案为:B。
先观察图形A到图形C的旋转方向,然后找到对应的边,确定旋转的角度。
10.C
解:15÷=90000000(厘米)=900(千米)。
故答案为:C。
实际距离=图上距离÷比例尺。
11.错误
解:比例的外项积一定等于内项积
故答案为:错误。
根据比例的基本性质( 在一个比例中,两个外项的积等于两个内项的积 )进行判断即可。
12.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
13.错误
解:比例尺不能带单位,原题干说法错误。
故答案为:错误。
比例尺是图上距离和实际距离的比,是一个比,不能带单位。
14.错误
解:圆柱的侧面展开图可以是长方形、正方形或平行四边形。
故答案为:错误。
圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
15.错误
解:今天的气温比昨天下降了5℃,今天的最低气温不确定。
故答案为:错误。
因为昨天的气温未知,所以今天的最低气温不确定。
16.5.4
解:4.5×1.2=5.4(平方分米)
故答案为:5.4。
这个长方形铁皮的面积就是圆柱的侧面积,由此用铁皮的长乘宽求出面积即可。
17.8∶14=24∶42
解:设第一项为x,第二项为x+6,第三项为3x
7x=4(x+6)
7x=4x+24
3x=24
x=8
x+6=8+6=14
3x=3×8=24
24÷=42
故答案为:8:14=24:42。
分析题干,已知前三项的关系,故假设第一项为x,则第二项为x+6,第三项为3x,又已知两个比的比值都是,故可得出第一项与第二项的比为,即,根据比例的基本性质(内项积=外项积),解出x的值为8,即第一项为8,进而得出第二项为14,第三项为24;已知第三项的值和比值,求第四项,24:第四项=,故第四项=24÷=42。
18.9;27
解:设原圆柱的底面半径为r,高为h。
原侧面积=2πrh,原体积=πr2h
扩大后的侧面积=2π(3r)(3h)=9( 2πrh),即侧面积扩大为原来的9倍;
扩大后的体积=π(3r)2(3h)=27πr2h,即体积扩大为原来的27倍。
故答案为:9;27。
圆柱的侧面积=底面周长×高=2×圆周率×半径×高,圆柱的体积=圆周率×半径的平方×高,根据公式分别将扩大后的半径与高代入并化简即可解答。
19.576
解:10×10=100(个)
26×26=676(个)
676-100=576(个)
一个由两位数字组成的密码,那密码第一位就可能是0,1,2,3,4,5,6,7,8,9共10种可能,而第二位同样有以上10种可能,所以一共就有10×10=100种组合可能;
如果由两个大写字母组成,那么密码第一位就可能是A,B,C……共26种可能,第二位同样有26种可能,所以一共就有26×26=676种可能,那么对比数字密码密码个数就增加了676-100=576个。
20.31.4;20
解:3.14×10=31.4(cm)
所以这个长方形的长是31.4cm,宽是20cm。
故答案为:31.4;20。
将圆柱侧面沿高展开后得到一个长方形,这个长方形的长是圆柱底面圆的周长,宽是圆柱的高。
21.-120
解:潜水艇上浮50米,记作+50米,小下潜120米应记作-120米;
故答案为:-120。
正、负数表示具有相反意义的量,因此,上浮记为“+“时,下潜就记为“-”,据此解答。
22.反;正
解:由=C(B不等于0) ,可得B×C=A(一定),乘积一定,所以B和C成反比例;
=C(一定),比值一定,A和B成正比例;
故答案为:反;正。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系;据此解答。
23.20:1
解:14cm=140mm
140:7=20:1
故答案为:20:1。
比例尺=图上距离:实际距离,据此代入数值计算即可。
24.8:15
解:甲数×=乙数×,所以甲数:乙数=:=8:15;
故答案为:8:15。
由题意可知,甲数×=乙数×,再根据比的基本性质:内项积等于外项积,将等式写成比例形式即可。
25.48;500
解:240-240×80%
=240-192
=48(元)
400÷80%=500(元)
故答案为:48;500。
求可以节省多少钱,就是先求出折后价格,再用原价减去折后价格,就可以求出了;
求原价,根据公式,原价=现价÷折扣,代入数值计算即可。
26.10.4+ =11 ÷70%= 1÷10%=10 0÷1%=0
24×25%=6 1-75%=0.25 180%- =1 2×80%=1.6
含有百分数的计算,把百分数化成分数或小数,然后再计算。
27.(1)33%x=16.5
解:x=16.5 ÷33%
x=50
(2) x-25%x=12
解:0.75x=12
x=12 ÷0.75
x=16
(3)160%x+4.5×20%=8.9
解: 160%x+0.9=8.9
160%x=8.9-0.9
x=8÷160%
x=5
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
(1)、(2)运用等式的性质2解方程;
(3)综合运用等式的性质解方程。
28.解:设甲商品的成本是x元,则乙商品的成本就是(2200-x)元, 0.9×(1.2x+2530-1.15x)=2331 0.05x+2530=2331÷0.9 0.05x=2590-2530 x=60÷0.05 x=1200答:甲商品的成本是1200元.
设甲商品的成本是x元,则乙商品的成本就是(2200-x)元,等量关系:(甲的售价+乙的售价)×90%=总成本+131,根据等量关系列出方程,解方程求出甲商品的成本即可.
29.解:实际距离=18÷=5400(厘米)
图上距离=5400×=27(厘米)
答:在另一幅比例尺为1∶200的地图上,这两地间的距离应是27厘米。
已知图上距离和比例尺,根据实际距离=图上距离÷比例尺,计算得出甲、乙两地的实际距离为18÷=5400(厘米);在另一幅地图上比例尺是1:200,根据图上距离=实际距离×比例尺计算即可。
30.解:×3.14×()2×10÷[3.14×()2]
=×3.14×36×10÷[3.14×100]
=376.8÷314
=1.2(厘米)
答:当铅锤取出后,杯中的水面会下降1.2厘米。
取出铅锤时,水面下降的高度=铅锤的体积÷圆柱形容器的底面积;其中,圆锥的体积=π×半径2×高÷3;底面积=π×半径2。
31.解:圆锥的高:
60÷2×2÷(5×2)
=60÷10
=6(厘米)
×3.14×52×6
=×3.14×25×6
=157(立方厘米)
答:这个圆锥的体积是157立方厘米
切成两半后表面积增加了2个三角形的面积,三角形的底是圆锥的底面直径,高是圆锥的高。因此用表面积增加的部分除以2求出一个三角形的面积。用三角形面积的2倍除以底求出高。然后根据圆锥的体积公式计算体积即可。
32.解:9.42÷3.14÷2
=3÷2
=1.5(米)
1.52×3.14×1.2÷3
=0.9×3.14
=2.826(立方米)
2.826×750
=2119.5(千克)
2119.5≈2120
答:这堆小麦大约重2120千克。
圆锥的体积=底面积×高÷3;底面积=半径×半径×π。
33.(1)解:8÷2=4(分米)
4÷2=2(分米)
3.14×22×8
=3.14×4×8
=12.56×8
=100.48(立方分米)
=100.48(升)
答:做成的这个圆柱形油桶的容积是100.48升。
(2)解:长:3.14×4+4
=12.56+4
=16.56(分米)
16.56×8=132.48(平方分米)
答:原来的长方形铁皮面积是132.48平方分米。
(1)观察图可知,要求这个圆柱的容积,先求出圆柱的底面半径和高,然后用公式:V=πr2h,据此列式计算;
(2)观察图可知,要求原来长方形铁皮的面积,先分别求出长与宽,然后用公式:长方形的面积=长×宽,据此列式解答。
2024-2025学年六年级下册期中测试卷(人教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.甲数的一半与乙数的相等(甲、乙两数都不为0),则甲数∶乙数=( )。
A.2∶ B.3∶4 C.4∶3 D.∶2
2. 一个比例中,两内项的积是3,一个外项是0.75,另一外项是( )。
A.4 B.3 C. D.
3.如图,圆柱形容器的底面半径为10cm,水的高度为12 cm,水中浸没着一个底面半径为4 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm。根据以上信息,不能解决的问题是( )。(容器的厚度忽略不计)
A.容器内装了多少水 B.铅锤的体积是多少
C.铅锤的高是多少 D.容器的高是多少
4.把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,( )。
A.面积扩大到原来的2倍 B.周长扩大到原来的2倍
C.面积扩大到原来的 D.周长缩小到原来的
5.图上距离一定时,比例尺与实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.一个圆柱的底面直径是10厘米,若高增加2厘米,则侧面积增加( )平方厘米。
A.3.14 B.31.4 C.62.8 D.6.28
7.学校今年的水电费比去年节约二成,表示今年的水电费是去年的( )。
A.20% B.120% C.80% D.12%
8.某服装店在进价的基础上提高两成后作为标价,照这样计算,一件进价420元的衣服应标价多少元?正确的列式是( )。
A.420×20% B.420×(1+20%)
C.420÷(1-20%) D.420×(1-20%)
9.图形 A 如何旋转得到图形C?下列选项中正确的是( )。
A.图形 A绕点O顺时针旋转 90°得到图形C
B.图形 A 绕点O 逆时针旋转 90°得到图形C
C.图形A绕点O 逆时针旋转 180°得到图形
D.再绕点O逆时针旋转 90°得到图形C
10.在比例尺是1:6000000的地图上,量得南京到北京的距离是15厘米,南京到北京的实际距离大约是( )
A.800千米 B.90千米 C.900千米 D.80千米
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.在一个比例中,外项积不一定等于内项积。( )
12.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
13.一幅地图的比例尺是1:1000000km。( )
14.圆柱的侧面展开图可以是长方形、平行四边形或梯形。( )
15.今天的气温比昨天下降了5℃,今天的最低气温是-5℃。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.用一张长4.5分米,宽1.2分米的长方形铁皮制成一个圆柱,这个圆柱的侧面积最多是 平方分米。(接口处不计)
17.一个比例的各项都是整数,它的两个比的比值都是,且第二项比第一项大6,第三项是第一项的3倍,这个比例是 。
18.一个圆柱底面半径和高都扩大为原来的3倍,侧面积就扩大为原来的 倍,体积就扩大为原来的 倍。
19.一个由两位数字组成的密码改为由两个大写字母组成的密码,密码总数增加 个。
20.一个圆柱的底面直径是10cm,高是20cm,将它的侧面沿高展开后得到一个长方形。这个长方形的长是 cm,宽是 cm。
21.潜水艇上浮50米,记作+50米,小下潜120米应记作 米。
22.=C(B不等于0)当A一定时,B和C成 比例,当C一定时,A和B成 比例。
23. 一个零件长7mm,画在设计图上是14cm,这幅设计图的比例尺是 。
24.甲数的等于乙数的(甲乙不等于0)甲数与乙数的最简比是 。
25.超市促销活动中所有商品一律八折,一件原价240元的衣服,现在买可以节省 元;王阿姨在促销活动中花400元购买了一套家电,原价 元。
阅卷人 四、计算题(23分)
得分
26.直接写出得数
10.4+ = ÷70%= 1÷10%= 0÷1%=
24×25%= 1-75%= 180%- = 2×80%=
27.解方程
(1)33%x=16.5
(2)x-25%x=12
(3)160%x+4.5×20%=8.9
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价。后来都按定价的九折打折出售,结果仍获利131元。甲商品的成本是多少元
29.在一幅比例尺是1∶300的地图上量得甲、乙两地相距18厘米,那么在另一幅比例尺为1∶200的地图上,这两地间的距离应是多少厘米?
30.底面直径是20厘米的圆柱形容器中装有一些水,将一个高是10厘米,底面直径是12厘米的圆锥形铅锤浸没入水中,取出铅锤时,水面下降多少?
31.如图,一个圆锥的底面半径是5cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积增加了60cm2.这个圆锥的体积是多少立方厘米?
32.打谷场有一个近似于圆锥形的小麦堆,测得底面周长是9.42m,高是1.2m,每立方米小麦约重750kg。这堆小麦大约重多少千克?(得数精确到整千克)
33.有张长方形的铁皮(如下图),李师傅剪下图中的阴影部分,正好可以做成一个高是8分米的圆柱形油桶。
(1)做成的这个圆柱形油桶的容积是多少升?(铁皮厚度不计)
(2)原来的长方形铁皮面积是多少平方分米?
答案解析部分
1.C
解:甲数×=乙数×
甲数:乙数=:
甲数:乙数=4:3
故答案为:C。
由甲数的一半与乙数的可得:甲数×=乙数×,然后根据比例的基本性质(内项积=外项积),得到比例形式甲数:乙数=:,最后将:进行化简即可。
2.A
解:3÷0.75=4。
故答案为:A。
另一个外项=两个内项积÷一个外项。
3.D
解:A项:已知圆柱形容器的底面半径和水的高度,用圆柱形容器的底面积乘水的高度,可求出容器内水的体积;
B项:把铅锤从水中取出后,水面下降了0.7cm,水面下降部分的体积即为铅锤的体积;
C项:已知铅锤的底面半径,可求出铅锤的底面积,进而求出铅锤的高;
D项:容器的高未知,容器的容积也未知,无法求出容器的高是多少厘米。
故答案为:D。
首先,题目给出圆柱容器的底面半径(10cm)、初始水高(12cm),以及取出圆锥铅锤后水面下降的高度(0.7cm)。通过这些信息,可以计算铅锤的体积,进而推导铅锤的高。同时,容器内原有水量可通过圆柱体积公式直接计算。但容器的总高度无法通过现有数据确定,因为题目未提供容器是否装满或铅锤取出后的水位高度与容器高度的关系,所以无法求出容器的高是多少厘米。
4.B
把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,周长扩大到原来的2倍.
故答案为:B.
把一个正方形接2:1的比例放大后,得到的图形与原来的图形相比较,边长扩大了2倍,所以周长扩大到原来的2倍,面积扩大到原来的4倍,据此解答.
5.B
解:实际距离×比例尺=图上距离(一定),图上距离一定时,比例尺与实际距离成反比例。
故答案为:B。
实际距离×比例尺=图上距离(一定),乘积一定,比例尺与实际距离成反比例。
6.C
解:侧面积增加10×3.14×2=62.8平方厘米。
故答案为:C。
侧面积增加的面积=底面周长×高增加的长度,其中底面周长=底面直径×π。
7.C
解:1-20%=80%。
故答案为:C。
今年的水电费比去年节约二成,把去年的水电费看作单位“1”,即今年的水电费是去年水电费的(1-20%);据此解答。
8.B
解:标价是进价的(1+20%),已知进价,求标价,用乘法计算,列式是420×(1+20%)。
故答案为:B。
根据题意可知,标价是进价的(1+20%),已知进价,求标价,用乘法计算。
9.A
解:图形A绕点O逆时针旋转 90°得到图形C。
故答案为:B。
先观察图形A到图形C的旋转方向,然后找到对应的边,确定旋转的角度。
10.C
解:15÷=90000000(厘米)=900(千米)。
故答案为:C。
实际距离=图上距离÷比例尺。
11.错误
解:比例的外项积一定等于内项积
故答案为:错误。
根据比例的基本性质( 在一个比例中,两个外项的积等于两个内项的积 )进行判断即可。
12.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
13.错误
解:比例尺不能带单位,原题干说法错误。
故答案为:错误。
比例尺是图上距离和实际距离的比,是一个比,不能带单位。
14.错误
解:圆柱的侧面展开图可以是长方形、正方形或平行四边形。
故答案为:错误。
圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
15.错误
解:今天的气温比昨天下降了5℃,今天的最低气温不确定。
故答案为:错误。
因为昨天的气温未知,所以今天的最低气温不确定。
16.5.4
解:4.5×1.2=5.4(平方分米)
故答案为:5.4。
这个长方形铁皮的面积就是圆柱的侧面积,由此用铁皮的长乘宽求出面积即可。
17.8∶14=24∶42
解:设第一项为x,第二项为x+6,第三项为3x
7x=4(x+6)
7x=4x+24
3x=24
x=8
x+6=8+6=14
3x=3×8=24
24÷=42
故答案为:8:14=24:42。
分析题干,已知前三项的关系,故假设第一项为x,则第二项为x+6,第三项为3x,又已知两个比的比值都是,故可得出第一项与第二项的比为,即,根据比例的基本性质(内项积=外项积),解出x的值为8,即第一项为8,进而得出第二项为14,第三项为24;已知第三项的值和比值,求第四项,24:第四项=,故第四项=24÷=42。
18.9;27
解:设原圆柱的底面半径为r,高为h。
原侧面积=2πrh,原体积=πr2h
扩大后的侧面积=2π(3r)(3h)=9( 2πrh),即侧面积扩大为原来的9倍;
扩大后的体积=π(3r)2(3h)=27πr2h,即体积扩大为原来的27倍。
故答案为:9;27。
圆柱的侧面积=底面周长×高=2×圆周率×半径×高,圆柱的体积=圆周率×半径的平方×高,根据公式分别将扩大后的半径与高代入并化简即可解答。
19.576
解:10×10=100(个)
26×26=676(个)
676-100=576(个)
一个由两位数字组成的密码,那密码第一位就可能是0,1,2,3,4,5,6,7,8,9共10种可能,而第二位同样有以上10种可能,所以一共就有10×10=100种组合可能;
如果由两个大写字母组成,那么密码第一位就可能是A,B,C……共26种可能,第二位同样有26种可能,所以一共就有26×26=676种可能,那么对比数字密码密码个数就增加了676-100=576个。
20.31.4;20
解:3.14×10=31.4(cm)
所以这个长方形的长是31.4cm,宽是20cm。
故答案为:31.4;20。
将圆柱侧面沿高展开后得到一个长方形,这个长方形的长是圆柱底面圆的周长,宽是圆柱的高。
21.-120
解:潜水艇上浮50米,记作+50米,小下潜120米应记作-120米;
故答案为:-120。
正、负数表示具有相反意义的量,因此,上浮记为“+“时,下潜就记为“-”,据此解答。
22.反;正
解:由=C(B不等于0) ,可得B×C=A(一定),乘积一定,所以B和C成反比例;
=C(一定),比值一定,A和B成正比例;
故答案为:反;正。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系;据此解答。
23.20:1
解:14cm=140mm
140:7=20:1
故答案为:20:1。
比例尺=图上距离:实际距离,据此代入数值计算即可。
24.8:15
解:甲数×=乙数×,所以甲数:乙数=:=8:15;
故答案为:8:15。
由题意可知,甲数×=乙数×,再根据比的基本性质:内项积等于外项积,将等式写成比例形式即可。
25.48;500
解:240-240×80%
=240-192
=48(元)
400÷80%=500(元)
故答案为:48;500。
求可以节省多少钱,就是先求出折后价格,再用原价减去折后价格,就可以求出了;
求原价,根据公式,原价=现价÷折扣,代入数值计算即可。
26.10.4+ =11 ÷70%= 1÷10%=10 0÷1%=0
24×25%=6 1-75%=0.25 180%- =1 2×80%=1.6
含有百分数的计算,把百分数化成分数或小数,然后再计算。
27.(1)33%x=16.5
解:x=16.5 ÷33%
x=50
(2) x-25%x=12
解:0.75x=12
x=12 ÷0.75
x=16
(3)160%x+4.5×20%=8.9
解: 160%x+0.9=8.9
160%x=8.9-0.9
x=8÷160%
x=5
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
(1)、(2)运用等式的性质2解方程;
(3)综合运用等式的性质解方程。
28.解:设甲商品的成本是x元,则乙商品的成本就是(2200-x)元, 0.9×(1.2x+2530-1.15x)=2331 0.05x+2530=2331÷0.9 0.05x=2590-2530 x=60÷0.05 x=1200答:甲商品的成本是1200元.
设甲商品的成本是x元,则乙商品的成本就是(2200-x)元,等量关系:(甲的售价+乙的售价)×90%=总成本+131,根据等量关系列出方程,解方程求出甲商品的成本即可.
29.解:实际距离=18÷=5400(厘米)
图上距离=5400×=27(厘米)
答:在另一幅比例尺为1∶200的地图上,这两地间的距离应是27厘米。
已知图上距离和比例尺,根据实际距离=图上距离÷比例尺,计算得出甲、乙两地的实际距离为18÷=5400(厘米);在另一幅地图上比例尺是1:200,根据图上距离=实际距离×比例尺计算即可。
30.解:×3.14×()2×10÷[3.14×()2]
=×3.14×36×10÷[3.14×100]
=376.8÷314
=1.2(厘米)
答:当铅锤取出后,杯中的水面会下降1.2厘米。
取出铅锤时,水面下降的高度=铅锤的体积÷圆柱形容器的底面积;其中,圆锥的体积=π×半径2×高÷3;底面积=π×半径2。
31.解:圆锥的高:
60÷2×2÷(5×2)
=60÷10
=6(厘米)
×3.14×52×6
=×3.14×25×6
=157(立方厘米)
答:这个圆锥的体积是157立方厘米
切成两半后表面积增加了2个三角形的面积,三角形的底是圆锥的底面直径,高是圆锥的高。因此用表面积增加的部分除以2求出一个三角形的面积。用三角形面积的2倍除以底求出高。然后根据圆锥的体积公式计算体积即可。
32.解:9.42÷3.14÷2
=3÷2
=1.5(米)
1.52×3.14×1.2÷3
=0.9×3.14
=2.826(立方米)
2.826×750
=2119.5(千克)
2119.5≈2120
答:这堆小麦大约重2120千克。
圆锥的体积=底面积×高÷3;底面积=半径×半径×π。
33.(1)解:8÷2=4(分米)
4÷2=2(分米)
3.14×22×8
=3.14×4×8
=12.56×8
=100.48(立方分米)
=100.48(升)
答:做成的这个圆柱形油桶的容积是100.48升。
(2)解:长:3.14×4+4
=12.56+4
=16.56(分米)
16.56×8=132.48(平方分米)
答:原来的长方形铁皮面积是132.48平方分米。
(1)观察图可知,要求这个圆柱的容积,先求出圆柱的底面半径和高,然后用公式:V=πr2h,据此列式计算;
(2)观察图可知,要求原来长方形铁皮的面积,先分别求出长与宽,然后用公式:长方形的面积=长×宽,据此列式解答。
同课章节目录
