2024-2025学年七年级下学期数学期中考试(嘉兴市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中考试(嘉兴市专用)[答案+解析] |

|
|
| 格式 | docx | ||
| 文件大小 | 247.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期中考试(嘉兴市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中一个最符合题意的正确选项,不选、多选、错选,均不给分)
1.叶绿体是植物进行光合作用的场所,某种叶绿体的直径约米.将数据用科学记数法表示为( )
A. B. C. D.
2.如图,小明用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形,则长方形的对角线长为( )
A. B.2 C. D.4
3.下列计算中,正确的是( )
A. B. C. D.
4.下列方程:①,②,③,④,⑤是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
5.解方程组,将①②得( )
A. B. C. D.
6.下列式子从左到右的变形属于因式分解的是( )
A. B.
C. D.
7.如图,一张长方形纸折叠后压平,点F在线段上,为两条折痕,若,,则的度数为( )
A. B. C. D.
8.古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉元,每斤鱼元,可列方程组为( )
A. B.
C. D.
9.因式分解的结果是( )
A. B. C. D.
10.将正方形①,正方形②,长方形③,长方形④按如图所示放入长方形ABCD中(相邻的长方形,正方形之间既无重叠,又无空隙),且BE=DP.若已知长方形ABCD的周长,则不能确定周长的图形是( )
A.正方形① B.正方形② C.长方形③ D.长方形④
二、填空题(本题有6小题,每题3分,共18分)
11.因式分解: .
12.已知二元一次方程,用含的代数式表示,则
13. 为增强学生体质, 某学校将 "抖空竹"引入阳光体育一小时活动。图 1 是一位同学抖空竹时的一个瞬间,小明把它抽象成图 2 的数学问题:已 , . 则 的度数是 。
14.①水平运输带运输物体; ②高楼电梯上上下下迎送宾客;③教室的门打开或关上;④教室铝合金窗户的滑动; ⑤游乐园里过山车的运动.上述现象中属于平移的是 . (填序号)
15.已知关于x,y的二元一次方程的解如表:
x … 0 1 …
y … 4 2 …
关于x,y的二元一次方程的解如表:
x … 0 1 …
y … 4 1 …
则关于x,y的二元一次方程组的解是 .
16.如果成立,则 .
三、解答题(本题有8小题,共52分,其中17~22每题6分:23、24题每题8分)
17.计算或化简:
(1);
(2)(﹣x2)3+2x3 x2;
(3)(8a3b﹣5a2b2)÷4ab.
18.把下列多项式分解因式:
(1)
(2)
19.解方程组
20.计算
(1).(要求简便计算)
(2)先化简,再求值:,其中.
21.如图,在Rt中,CD为斜边AB的中线,在边AD及CD的延长线上依次取点E,F,且.
(1)求证:.
(2)若,求的度数.
22.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;…
按照以上规律,解决下列问题:
(1)写出第6个等式:___________;
(2)写出你猜想的第n(n取正整数)个等式:________(用含n的等式表示),并验证等式的正确性.
23.若x满足,求的值.
解:设,则
∴.
请仿照上面的方法求解下面问题:
(1)若x满足,求的值;
(2)若x满足,求代数式的值;
(3)已知正方形ABCD的边长为x、E、F分别是AD、DC上的点,且,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.
24.根据以下素材,探索完成任务.
如何设计板材裁切方案?
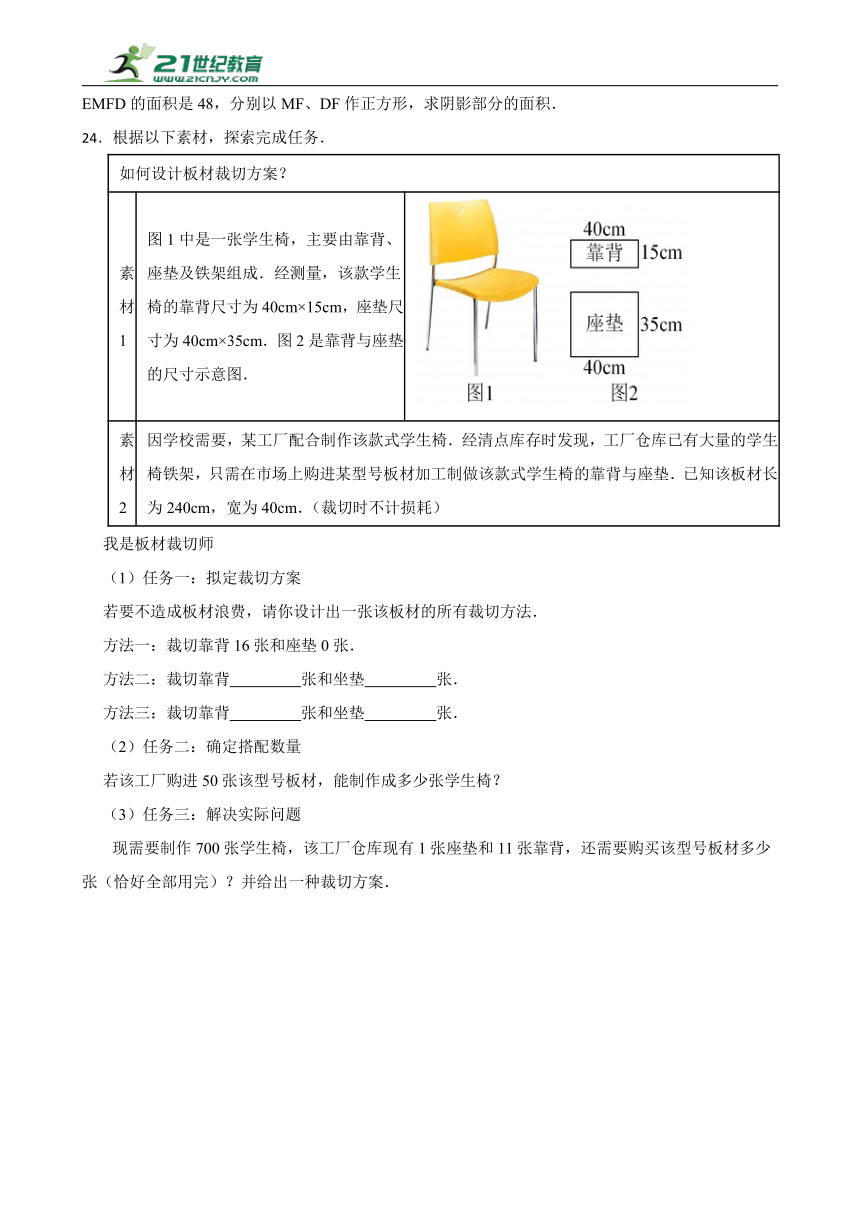
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm.(裁切时不计损耗)
我是板材裁切师
(1)任务一:拟定裁切方案
若要不造成板材浪费,请你设计出一张该板材的所有裁切方法.
方法一:裁切靠背16张和座垫0张.
方法二:裁切靠背 张和坐垫 张.
方法三:裁切靠背 张和坐垫 张.
(2)任务二:确定搭配数量
若该工厂购进50张该型号板材,能制作成多少张学生椅?
(3)任务三:解决实际问题
现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
答案解析部分
1.D
2.C
解:∵正方形的对角线为2,
∴①和②的直角边都为1,
∴长方形的长为2,宽为1,
∴长方形的对角线长为.
故答案为:C
观察图形正方形,利用正方形的对角线长为2,可得到①和②的两直角边的长,再观察长方形,可知长方形的长为2,宽为1,然后利用勾股定理求出长方形的对角线长.
3.D
4.B
解:①符合二元一次方程的定义,故①是二元一次方程;
②不是整式方程,不符合二元一次方程的定义,故②不是二元一次方程;
③含有3个未知数,不符合二元一次方程的定义,故③不是二元一次方程;
④不是等式,不符合二元一次方程的定义,故④不是二元一次方程;
⑤符合二元一次方程的定义,故⑤是二元一次方程;
故是二元一次方程是①⑤,共2个,
故选:B
本题主要考查二元一次方程的概念,把只含有2个未知数,未知数的最高次数是1的整式方程,称为二元一次方程,据此逐项分析作答,即可得到答案.
5.B
解:①②得:,
去括号,得:,
合并同类项得:,
故答案为:.
利用加减消元法的计算方法及步骤分析求解即可.
6.D
7.A
解:由折叠的性质可得,
∴,
∴,
又∵,
∴,
故答案为:A.
利用折叠可得,即可得到,然后根据平角的定义可得,解题即可案.
8.A
解:∵77元钱共买了10斤肉和3斤鱼
∴10x+3y=77;
∵9斤肉的钱等于5斤鱼的钱,
∴9x=5y.
∴根据题意可列出方程组;
故答案为:A.
根据“77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱”,即可列出关于x,y的二元一次方程组,即可求解.
9.B
10.B
解:设长方形ABCD的周长为C,AE=x,DP=y,则C=2(AD+AB)=2[(AE+BE)+(AG+GD)]=2[(AE+DP)+(AE+PQ)=2[(AE+DP)+(AE+AE-DP)]=2[(x+y)+(x+x-y)]=6x.
所以.正方形① 的周长=4AE=,故能确定周长;长方形③的周长=2(GD+DP)=2(PQ+PD)=2(AE-DP+DP)=2AE=,故能确定周长;长方形④ 的周长=2(BC+BE)=2(AE+AE-DP+DP)=4AE=,故能确定周长.故A、C、D均不符合.
故答案为:B.
分别计算四个图形的周长,看是否能用长方形ABCD的周长表示,找出不能的即可.
11.
12.2x-5
解:,
移项得y=2x-5.
故答案为:2x-5..
直接移项求出y即可.
13.30°
14.①②④
解:①水平运输带运输物体是沿直线运动,符合平移的定义,符合题意;
②高楼电梯上上下下迎送宾客是沿直线运动,符合平移的定义,符合题意;
③教室的门打开或关上不是沿直线运动,不符合平移的定义,不符合题意;
④ 教室铝合金窗户的滑动是沿直线运动,符合平移的定义,符合题意;
⑤ 游乐园里过山车的运动不是沿直线运动,不符合平移的定义,不符合题意.
故答案为:①②④.
在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;根据平移的定义并结合每一个命题即可判断求解.
15.
解:∵从第一个表格中可知,当时,,时,,
∴,
解得:,
把代入得:
,
整理得:,
∵从第二个表格中可知,当时,,时,,
∴,
解得:,
把代入得:
,
整理得:,
①和②组成方程组,
解得:
故答案为:.
故答案为:
要解关于的方程组 ,可利用待定系数法先求出系数的值,再分别把代入第一个方程中,把代入到第二个方程中,化简可得到关于的二元一次方程组,最后再求解即可.
16.2或
17.(1)解:
=1﹣8
=﹣7;
(2)解:(﹣x2)3+2x3 x2=﹣x6+2x5;
(3)解:(8a3b﹣5a2b2)÷4ab
=8a3b÷4ab﹣5a2b2÷4ab
=2a2ab.
(1)先根据零次方、负整数指数幂的运算规律计算,再根据有理数的减法法则计算即可;
(2)根据幂的乘方、同底数幂的乘法计算即可;
(3)根据多项式除以单项式法则计算即可.
18.(1)解:原式
(2)解:原式=
=
(1)先提取各项的公因式x,再利用平方差公式将剩下的式子继续分解到每一个因式都不能再分解为止;
(2)把“2a-b”看成一个整体,先利用添括号法则把原式变形,再利用提公因式法分解即可.
(1)解:
(2)
19.解:
解:将①整理,得x=-5y③,将③代入②,得2×(-5y)-5y=7,
-15y=7,
解得:y=-.
将y=-代入②得:x=,
∴原方程组的解为
先把方程①整理成用含y的式子表示x的形式,再把它代入②,即可求出y的值,再把y的值代入③即可求出x的值,进而得到原方程组的解.
20.(1)解:原式
;
(2)解:原式
,
将代入,
原式.
(1)观察算式可把2024与2022分别表示成2023与1的和与差的形式,再利用平方差公式即可简化计算;
(2)整式的化简求值,必须先化简,再代入求值;化简时注意准确运用乘法公式、乘法分配律等可简化运算,另还要准确运用多项式除以单项式的运算法则,并在最后的加减运算中对出现的同类项予以合并.
(1)解:原式
;
(2)解:原式
,
将代入,
原式
21.(1)证明:在Rt中,∵CD为斜边AB的中线,
∴CD=BD,
∴∠DCB=∠B.
∵,
∴∠DCB=∠EFD,
又∵在边AD及CD的延长线上依次取点E,F,
∴EF//BC.
(2)解:∵是直角三角形,
∴∠A+∠B=90°,
∵,
∴65°+∠B=90°,解得:∠B=25°.
∵EF//BC,
∴∠FED=∠B=25°.
(1)先利用直角三角形中斜边上的中线的性质,得出CD=BD,再得出∠DCB=∠B,结合,可得出∠DCB=∠EFD,从而有EF//BC.
(2)先根据直角三角形的两个锐角互余,求得∠B,再利用平行线的性质求得∠AEF.
22.(1);
(2)
23.(1)5
(2)13
(3)28
24.(1)9;3;2;6
(2)解:根据题意,得=240(张).
答:该工厂购进50张该型号板材,能制作成240张学生椅.
(3)解:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张.
根据题意,得解得∴57+88=145(张).
答:需要购买该型号板材145张,用其中57张板材裁切靠背9张和坐垫3张,用88张板材裁切靠背2张和坐垫6张.
:(1)设裁切靠背m张,坐垫n张.根据题意,15m+35n=240,∴n=,然后求出非负整数解,
,m=9,n=3.m=2,n=6符合题意.
任务一:设裁切靠背x张,坐垫y张.根据题意,得15x + 35y = 240. 然后求出非负整数解即可;
任务二:根据题意,列式计算即可;
任务三:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,根据题意列方程组求解即可.
2024-2025学年七年级下册期中考试(嘉兴市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中一个最符合题意的正确选项,不选、多选、错选,均不给分)
1.叶绿体是植物进行光合作用的场所,某种叶绿体的直径约米.将数据用科学记数法表示为( )
A. B. C. D.
2.如图,小明用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形,则长方形的对角线长为( )
A. B.2 C. D.4
3.下列计算中,正确的是( )
A. B. C. D.
4.下列方程:①,②,③,④,⑤是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
5.解方程组,将①②得( )
A. B. C. D.
6.下列式子从左到右的变形属于因式分解的是( )
A. B.
C. D.
7.如图,一张长方形纸折叠后压平,点F在线段上,为两条折痕,若,,则的度数为( )
A. B. C. D.
8.古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉元,每斤鱼元,可列方程组为( )
A. B.
C. D.
9.因式分解的结果是( )
A. B. C. D.
10.将正方形①,正方形②,长方形③,长方形④按如图所示放入长方形ABCD中(相邻的长方形,正方形之间既无重叠,又无空隙),且BE=DP.若已知长方形ABCD的周长,则不能确定周长的图形是( )
A.正方形① B.正方形② C.长方形③ D.长方形④
二、填空题(本题有6小题,每题3分,共18分)
11.因式分解: .
12.已知二元一次方程,用含的代数式表示,则
13. 为增强学生体质, 某学校将 "抖空竹"引入阳光体育一小时活动。图 1 是一位同学抖空竹时的一个瞬间,小明把它抽象成图 2 的数学问题:已 , . 则 的度数是 。
14.①水平运输带运输物体; ②高楼电梯上上下下迎送宾客;③教室的门打开或关上;④教室铝合金窗户的滑动; ⑤游乐园里过山车的运动.上述现象中属于平移的是 . (填序号)
15.已知关于x,y的二元一次方程的解如表:
x … 0 1 …
y … 4 2 …
关于x,y的二元一次方程的解如表:
x … 0 1 …
y … 4 1 …
则关于x,y的二元一次方程组的解是 .
16.如果成立,则 .
三、解答题(本题有8小题,共52分,其中17~22每题6分:23、24题每题8分)
17.计算或化简:
(1);
(2)(﹣x2)3+2x3 x2;
(3)(8a3b﹣5a2b2)÷4ab.
18.把下列多项式分解因式:
(1)
(2)
19.解方程组
20.计算
(1).(要求简便计算)
(2)先化简,再求值:,其中.
21.如图,在Rt中,CD为斜边AB的中线,在边AD及CD的延长线上依次取点E,F,且.
(1)求证:.
(2)若,求的度数.
22.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;…
按照以上规律,解决下列问题:
(1)写出第6个等式:___________;
(2)写出你猜想的第n(n取正整数)个等式:________(用含n的等式表示),并验证等式的正确性.
23.若x满足,求的值.
解:设,则
∴.
请仿照上面的方法求解下面问题:
(1)若x满足,求的值;
(2)若x满足,求代数式的值;
(3)已知正方形ABCD的边长为x、E、F分别是AD、DC上的点,且,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.
24.根据以下素材,探索完成任务.
如何设计板材裁切方案?
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm.(裁切时不计损耗)
我是板材裁切师
(1)任务一:拟定裁切方案
若要不造成板材浪费,请你设计出一张该板材的所有裁切方法.
方法一:裁切靠背16张和座垫0张.
方法二:裁切靠背 张和坐垫 张.
方法三:裁切靠背 张和坐垫 张.
(2)任务二:确定搭配数量
若该工厂购进50张该型号板材,能制作成多少张学生椅?
(3)任务三:解决实际问题
现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
答案解析部分
1.D
2.C
解:∵正方形的对角线为2,
∴①和②的直角边都为1,
∴长方形的长为2,宽为1,
∴长方形的对角线长为.
故答案为:C
观察图形正方形,利用正方形的对角线长为2,可得到①和②的两直角边的长,再观察长方形,可知长方形的长为2,宽为1,然后利用勾股定理求出长方形的对角线长.
3.D
4.B
解:①符合二元一次方程的定义,故①是二元一次方程;
②不是整式方程,不符合二元一次方程的定义,故②不是二元一次方程;
③含有3个未知数,不符合二元一次方程的定义,故③不是二元一次方程;
④不是等式,不符合二元一次方程的定义,故④不是二元一次方程;
⑤符合二元一次方程的定义,故⑤是二元一次方程;
故是二元一次方程是①⑤,共2个,
故选:B
本题主要考查二元一次方程的概念,把只含有2个未知数,未知数的最高次数是1的整式方程,称为二元一次方程,据此逐项分析作答,即可得到答案.
5.B
解:①②得:,
去括号,得:,
合并同类项得:,
故答案为:.
利用加减消元法的计算方法及步骤分析求解即可.
6.D
7.A
解:由折叠的性质可得,
∴,
∴,
又∵,
∴,
故答案为:A.
利用折叠可得,即可得到,然后根据平角的定义可得,解题即可案.
8.A
解:∵77元钱共买了10斤肉和3斤鱼
∴10x+3y=77;
∵9斤肉的钱等于5斤鱼的钱,
∴9x=5y.
∴根据题意可列出方程组;
故答案为:A.
根据“77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱”,即可列出关于x,y的二元一次方程组,即可求解.
9.B
10.B
解:设长方形ABCD的周长为C,AE=x,DP=y,则C=2(AD+AB)=2[(AE+BE)+(AG+GD)]=2[(AE+DP)+(AE+PQ)=2[(AE+DP)+(AE+AE-DP)]=2[(x+y)+(x+x-y)]=6x.
所以.正方形① 的周长=4AE=,故能确定周长;长方形③的周长=2(GD+DP)=2(PQ+PD)=2(AE-DP+DP)=2AE=,故能确定周长;长方形④ 的周长=2(BC+BE)=2(AE+AE-DP+DP)=4AE=,故能确定周长.故A、C、D均不符合.
故答案为:B.
分别计算四个图形的周长,看是否能用长方形ABCD的周长表示,找出不能的即可.
11.
12.2x-5
解:,
移项得y=2x-5.
故答案为:2x-5..
直接移项求出y即可.
13.30°
14.①②④
解:①水平运输带运输物体是沿直线运动,符合平移的定义,符合题意;
②高楼电梯上上下下迎送宾客是沿直线运动,符合平移的定义,符合题意;
③教室的门打开或关上不是沿直线运动,不符合平移的定义,不符合题意;
④ 教室铝合金窗户的滑动是沿直线运动,符合平移的定义,符合题意;
⑤ 游乐园里过山车的运动不是沿直线运动,不符合平移的定义,不符合题意.
故答案为:①②④.
在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;根据平移的定义并结合每一个命题即可判断求解.
15.
解:∵从第一个表格中可知,当时,,时,,
∴,
解得:,
把代入得:
,
整理得:,
∵从第二个表格中可知,当时,,时,,
∴,
解得:,
把代入得:
,
整理得:,
①和②组成方程组,
解得:
故答案为:.
故答案为:
要解关于的方程组 ,可利用待定系数法先求出系数的值,再分别把代入第一个方程中,把代入到第二个方程中,化简可得到关于的二元一次方程组,最后再求解即可.
16.2或
17.(1)解:
=1﹣8
=﹣7;
(2)解:(﹣x2)3+2x3 x2=﹣x6+2x5;
(3)解:(8a3b﹣5a2b2)÷4ab
=8a3b÷4ab﹣5a2b2÷4ab
=2a2ab.
(1)先根据零次方、负整数指数幂的运算规律计算,再根据有理数的减法法则计算即可;
(2)根据幂的乘方、同底数幂的乘法计算即可;
(3)根据多项式除以单项式法则计算即可.
18.(1)解:原式
(2)解:原式=
=
(1)先提取各项的公因式x,再利用平方差公式将剩下的式子继续分解到每一个因式都不能再分解为止;
(2)把“2a-b”看成一个整体,先利用添括号法则把原式变形,再利用提公因式法分解即可.
(1)解:
(2)
19.解:
解:将①整理,得x=-5y③,将③代入②,得2×(-5y)-5y=7,
-15y=7,
解得:y=-.
将y=-代入②得:x=,
∴原方程组的解为
先把方程①整理成用含y的式子表示x的形式,再把它代入②,即可求出y的值,再把y的值代入③即可求出x的值,进而得到原方程组的解.
20.(1)解:原式
;
(2)解:原式
,
将代入,
原式.
(1)观察算式可把2024与2022分别表示成2023与1的和与差的形式,再利用平方差公式即可简化计算;
(2)整式的化简求值,必须先化简,再代入求值;化简时注意准确运用乘法公式、乘法分配律等可简化运算,另还要准确运用多项式除以单项式的运算法则,并在最后的加减运算中对出现的同类项予以合并.
(1)解:原式
;
(2)解:原式
,
将代入,
原式
21.(1)证明:在Rt中,∵CD为斜边AB的中线,
∴CD=BD,
∴∠DCB=∠B.
∵,
∴∠DCB=∠EFD,
又∵在边AD及CD的延长线上依次取点E,F,
∴EF//BC.
(2)解:∵是直角三角形,
∴∠A+∠B=90°,
∵,
∴65°+∠B=90°,解得:∠B=25°.
∵EF//BC,
∴∠FED=∠B=25°.
(1)先利用直角三角形中斜边上的中线的性质,得出CD=BD,再得出∠DCB=∠B,结合,可得出∠DCB=∠EFD,从而有EF//BC.
(2)先根据直角三角形的两个锐角互余,求得∠B,再利用平行线的性质求得∠AEF.
22.(1);
(2)
23.(1)5
(2)13
(3)28
24.(1)9;3;2;6
(2)解:根据题意,得=240(张).
答:该工厂购进50张该型号板材,能制作成240张学生椅.
(3)解:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张.
根据题意,得解得∴57+88=145(张).
答:需要购买该型号板材145张,用其中57张板材裁切靠背9张和坐垫3张,用88张板材裁切靠背2张和坐垫6张.
:(1)设裁切靠背m张,坐垫n张.根据题意,15m+35n=240,∴n=,然后求出非负整数解,
,m=9,n=3.m=2,n=6符合题意.
任务一:设裁切靠背x张,坐垫y张.根据题意,得15x + 35y = 240. 然后求出非负整数解即可;
任务二:根据题意,列式计算即可;
任务三:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,根据题意列方程组求解即可.
同课章节目录
