2024-2025学年七年级下学期数学期中考试(宁波专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中考试(宁波专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 429.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 09:33:01 | ||
图片预览



文档简介
保密★启用前
2024-2025学年七年级下册期中考试(宁波市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、温馨提示:在每小题给出的四个选项中,只有一项符合题目要求.
1.如图所示,下列结论中不正确的是
A.和是同位角 B.和是同旁内角
C.和是同位角 D.和是内错角
2.随着AI技术的发展,某机构预测,到2035年,全球AI市场规模将达到5510000000000元.数5510000000000用科学记数法表示为( )
A. B. C. D.
3.下列是二元一次方程的是( )
A. B. C. D.
4.已知多项式分解因式后有一个因式是,则的值为( )
A. B. C. D.
5.下列多项式乘法中可以用平方差公式计算的是( )
A. B.
C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.某学校为学生配备物理电学实验器材,一个电表包内装有1个电压表和2个电流表.某生产线共60名工人,每名工人每天可生产14个电压表或20个电流表.若分配名工人生产电压表,名工人生产电流表,恰好使每天生产的电压、电流表配成套,则可列出方程组( )
A. B.
C. D.
8.定义一种新运算“*”:,则( )
A.24 B.22 C. D.
9.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.下列判断正确的是( )
结论 Ⅰ :若n的值为5,则y的值为1;
结论Ⅱ:的值为定值;
结论Ⅲ:若,则y的值为4或1.
A.Ⅰ ,Ⅲ均对 B.Ⅱ对,Ⅲ错 C.Ⅱ错,Ⅲ对 D.Ⅰ ,Ⅱ均错
10.如图,将平行四边形沿对角线折叠,使点A落在点E处.若,,则的度数为( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.太阳到地球的距离约为 , 光的速度约为 , 则太阳光从太阳射到地球的时间约为 s.
12.若,则 .
13.因式分解: .
14.如图,将一个周长为厘米的三角形沿射线方向平移后得到三角形,点、、的对应点分别是点、、.连接,已知四边形的周长为厘米,那么平移的距离是 厘米.(用含、的代数式表示结果).
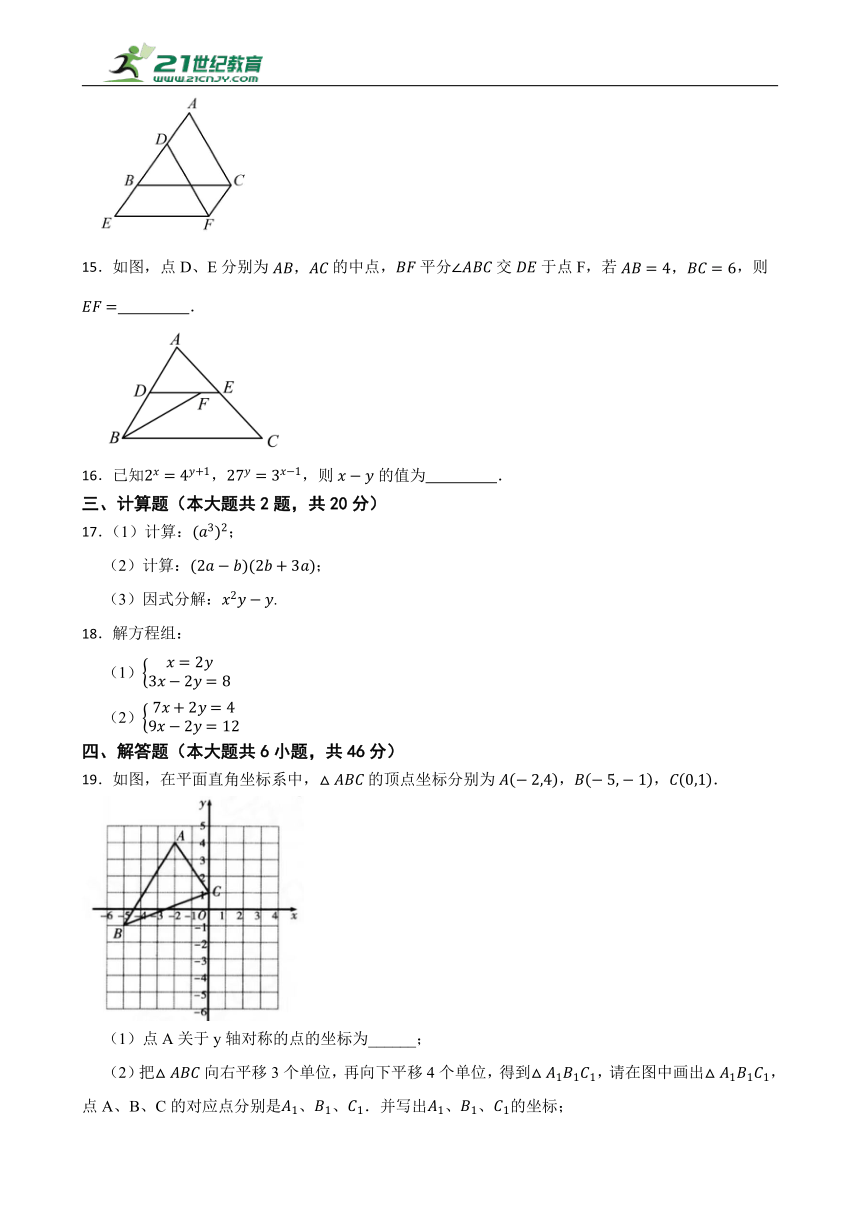
15.如图,点D、E分别为的中点,平分交于点F,若,则 .
16.已知,,则的值为 .
三、计算题(本大题共2题,共20分)
17.(1)计算:;
(2)计算:;
(3)因式分解:.
18.解方程组:
(1)
(2)
四、解答题(本大题共6小题,共46分)
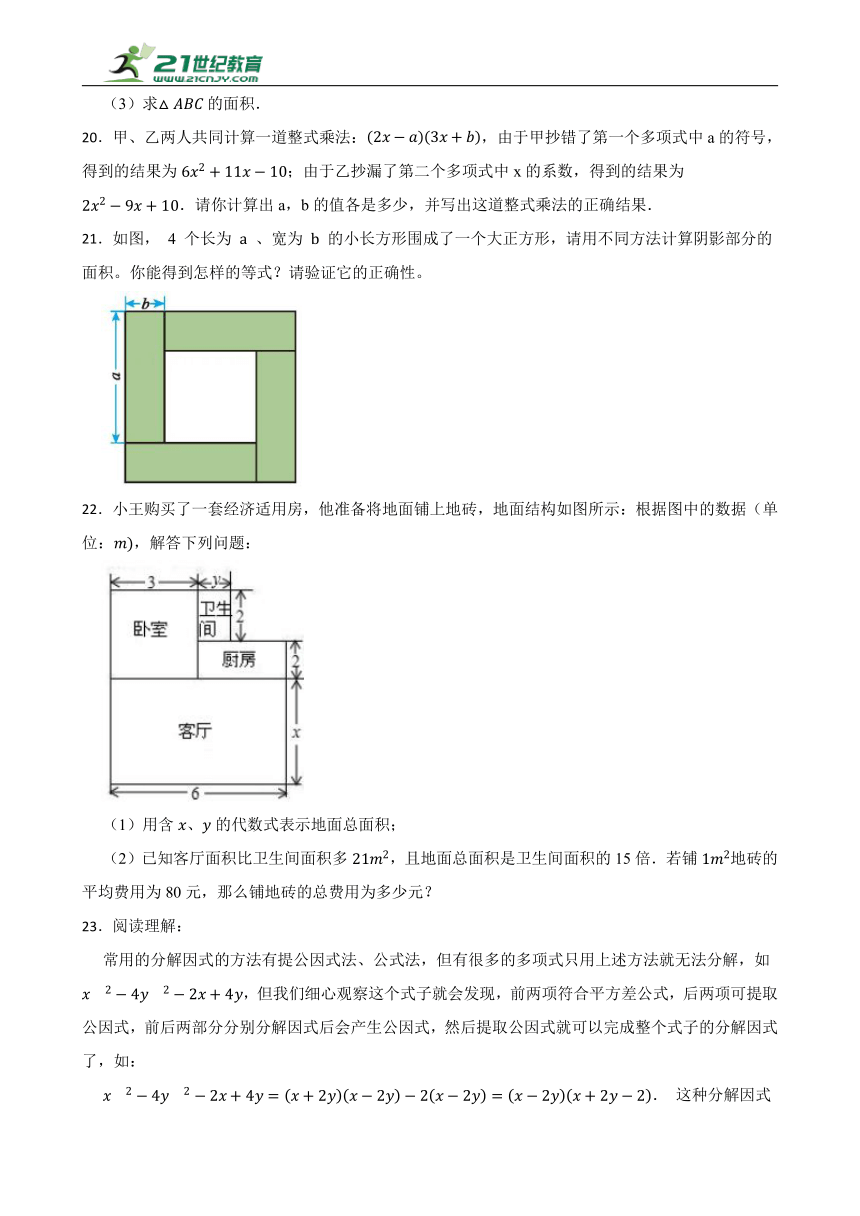
19.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)点A关于y轴对称的点的坐标为______;
(2)把向右平移3个单位,再向下平移4个单位,得到,请在图中画出,点A、B、C的对应点分别是、、.并写出、、的坐标;
(3)求的面积.
20.甲、乙两人共同计算一道整式乘法:,由于甲抄错了第一个多项式中a的符号,得到的结果为;由于乙抄漏了第二个多项式中x的系数,得到的结果为.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
21.如图, 4 个长为 、宽为 的小长方形围成了一个大正方形,请用不同方法计算阴影部分的面积。你能得到怎样的等式?请验证它的正确性。
22.小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示:根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多,且地面总面积是卫生间面积的15倍.若铺地砖的平均费用为80元,那么铺地砖的总费用为多少元?
23.阅读理解:
常用的分解因式的方法有提公因式法、公式法,但有很多的多项式只用上述方法就无法分解,如,但我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,如:
. 这种分解因式的方法叫分组分解法.
解决问题:
(1)分解因式:;
(2)三边满足,判断的形状.
24.如图1,直线MN与直线AB、CD分别交于点E、F,∠MEB与∠NFD互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化,若不变,请求出其值;若变化,说明理由.
答案解析部分
1.A
A、∠1和∠2是同旁内角,故本选项错误,符合题意;
B、∠2和∠3是同旁内角,故本选项正确,不符合题意;
C、∠1和∠4是同位角,故本选项正确,不符合题意;
D、∠2和∠4是内错角,故本选项正确,不符合题意;
故答案为:A.
利用同位角,内错角,同旁内角以及对顶角的定义逐项判断解题.
2.C
解:因为
故答案为:C.
用科学记数法表示绝对值较大数字时,常把这个数字表示成的形式,其中,的值取这个数字的位数减。
3.B
解:A:不是等式,故错误;
B:是二元一次方程,故正确;
C:,的次数为,故错误;
D:,含有三个未知数,故错误;
故选:B.
把只含有两个未知数且未知数的次数是1次的整式方程叫二元一次方程.
4.A
解:多项式分解因式后有一个因式是,
当时,多项式的值为,
即,
解得:,
故答案为:.
令时,多项式的值为,求出m值即可.
5.B
解:A. 不能用平方差公式进行计算,故A项符合题意;
B. , 能用平方差公式进行计算,故B项不符合题意;
C. 不能用平方差公式进行计算,故C项不符合题意;
D. 不能用平方差公式进行计算,故D项不符合题意;
故答案为:B.
根据平方差公式:(a+b)(a-b)=a2-b2,即可求得.
6.A
7.D
解:若分配名工人生产电压表,名工人生产电流表,
由题意,得.
故选:D.
本题考查了由实际问题抽象出二元一次方程组,设分配名工人生产电压表,名工人生产电流表,结合电压表数量和电流表数量的等量关系,列出二元一次方程组,即可得到答案.
8.A
9.B
解:由题意可得:,
②-①得:2x=n-m,
解得:,
把代入①得:,
解得:,
∵m+n=8,
∴当n=5时,m=3,
∴,
∴结论Ⅰ正确;
∵①+②得:4x+4y=8,
∴x+y=2,
∴结论Ⅱ正确;
∴当x=1时,y=1,满足 ,
∴m-3n=0,
∴m=3n,
∴m=6,n=2,
∴当x=-2,y=4时,满足,
当x=-1时,则y=3,
∴m=-1+2×3=5,n=-1×3+2×3=3,
∴m-3n=5-3×3=-4,满足,
综上所述:当 时,y的值为4或3或1,
∴结论Ⅲ错误;
故答案为:B.
根据题意先求出,再利用二元一次方程的解,零指数幂和负整数指数幂等计算求解即可。
10.D
解:根据折叠可知,,,
∵四边形为平行四边形,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:D.
根据折叠得出,,根据平行线的性质得出,得出,根据,求出,即可得出,根据三角形内角和定理求出结果即可.
11.
解:∵太阳到地球的距离约为 , 光的速度约为 ,
∴太阳光从太阳射到地球的时间约为:1.5×108÷3.0×105=0.5×103=5×102(s).
故答案为:5×102.
根据单项式除以单项式的法则“系数相除,同底数幂相除 ,只在被除式里的字母则连同它的指数作为积的一个因式“计算即可求解.
12.4.
解:∵a+2b=2,
∴2a+4b=2(a+2b)=2×2=4.
故答案为:4.
先将所求多项式用提公因式法进行因式分解,再整体代入求值即可.
13.
14.
15.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
16.3
解:∵,,
∴,解得:,
则.
故答案为:3.
利用幂的乘方运算性质将原式变形,列出方程组,解方程组即可求得x,y的值,再代入即可求得x-y的值.
17.(1)解:
(2)解:
(3)解:
.
(1)利用幂的乘方法则计算;
(2)利用多项式乘多项式法则计算;
(3)先求出公因式,再利用平方差公式分解因式.
18.(1)解:
把①代入②,得,
解得:,
把代入①,得,
∴方程组的解是.
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
∴方程组的解是.
(1)利用代入消元法的计算方法及步骤分析求解即可;
(2)利用加减消元法的计算方法及步骤分析求解即可.
(1)解:
把①代入②,得,
解得:,
把代入①,得,
所以方程组的解是;
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
所以方程组的解是.
19.(1)
(2)解:△ 如图所示:
由图可得:,,.
(3)解:的面积.
解:
(1),
点关于轴对称的点的坐标为;
故答案为:.
(1)根据关于y轴对称点的坐标变换规律:纵坐标不变,横坐标互为相反相成数求解即可;
(2)利用平移的性质:图形的平移即对应的点平移,因此可将点A、B、C 向右平移3个单位,再向下平移4个单位,得到、、 作出图形,再根据点的位置,写出坐标即可;
(3)利用网格,根据的面积=55的正方形面积减去三个直角三角形面积计算即可.
(1)解:,
点关于轴对称的点的坐标为.
故答案为:.
(2)解:△ 如图所示,
由图可得:,,.
(3)解:的面积.
20.,正确结果为
21.解:方法一:S阴影=(a+b)2-(a-b)2;方法二:S阴影=4ab;
∴可得等式:(a+b)2-(a-b)2=4ab;
证明:(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=4ab.
利用不同的表达式表示阴影部分的面积可得等式(a+b)2-(a-b)2=4ab;再利用完全平方公式的计算方法分析求解即可.
22.(1)解:地面总面积为:
(2)解:由题意得,解得:,
地面总面积为:,
铺地砖的总费用为:(元.
答:铺地砖的总费用为3600元.
(1)由图形可得:客厅的长为6,宽为x,厨房的长为3,宽为2,卫生间的长为2,宽为y,卧室的长为3,宽为4,然后根据矩形的面积公式进行解答;
(2)根据客厅面积比卫生间面积多21m2可得6x-2y=21,根据地面总面积是卫生间面积的15倍可得另一个x与y的方程,联立求出x、y的值,代入(1)的结果中求出地面的总面积,再乘以每平方米的费用即可求出总费用.
23.(1)
(2)等腰三角形
24.(1)解:如图1,AB∥CD,理由如下:
∵ ∠MEB与∠NFD互补 ,
∴∠MEB+∠NFD=180°,
又∵∠MEB=∠AEF,∠NFD=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)证明:如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°,
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵GH⊥EG,
∴PF∥GH;
(3)解:∠HPQ的大小不会发生变化,理由如下:
∵∠PHK=∠HPK
∴∠PKG=2∠HPK
∵GH⊥EG
∴∠KPG=90°-∠PKG=90°-2∠HPK
∴∠EPK=180°-∠KPG=90°+2∠HPK
∵PQ平分∠EPK
∴∠QPK=∠EPK=45°+∠HPK
∴∠HPQ=∠QPK-∠HPK=45°
∴∠HPQ的大小不会发生变化,其值为45°.
(1)根据补角的定义得∠MEB+∠NFD=180°,根据对顶角相等得∠MEB=∠AEF,∠NFD=∠CFE,从而可得∠AEF+∠CFE=180°,由同旁内角互补,两直线平行,得出结论AB∥CD;
(2)根据二直线平行,同旁内角互补得∠BEF+∠EFD=180°,根据角平分线的定义得∠FEP+∠EFP=(∠BEF+∠EFD)=90°,根据三角形的内角和定理得∠EPF=90°,即EG⊥PF,进而根据同一平面内垂直同一直线的两条直线互相平行可得PF∥GH;
(3)∠HPQ的大小不会发生变化,理由如下:根据三角形外角性质并结合∠PHK=∠HPK得∠PKG=2∠HPK,利用三角形外角定理、三角形内角和定理求得∠KPG=90° ∠PKG=90° 2∠HPK;再由邻补角的定义、角平分线的定义推得∠QPK=12∠EPK=45°+∠HPK;然后由图形中角与角的和差关系求得∠HPQ=45°即可.
2024-2025学年七年级下册期中考试(宁波市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、温馨提示:在每小题给出的四个选项中,只有一项符合题目要求.
1.如图所示,下列结论中不正确的是
A.和是同位角 B.和是同旁内角
C.和是同位角 D.和是内错角
2.随着AI技术的发展,某机构预测,到2035年,全球AI市场规模将达到5510000000000元.数5510000000000用科学记数法表示为( )
A. B. C. D.
3.下列是二元一次方程的是( )
A. B. C. D.
4.已知多项式分解因式后有一个因式是,则的值为( )
A. B. C. D.
5.下列多项式乘法中可以用平方差公式计算的是( )
A. B.
C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.某学校为学生配备物理电学实验器材,一个电表包内装有1个电压表和2个电流表.某生产线共60名工人,每名工人每天可生产14个电压表或20个电流表.若分配名工人生产电压表,名工人生产电流表,恰好使每天生产的电压、电流表配成套,则可列出方程组( )
A. B.
C. D.
8.定义一种新运算“*”:,则( )
A.24 B.22 C. D.
9.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.下列判断正确的是( )
结论 Ⅰ :若n的值为5,则y的值为1;
结论Ⅱ:的值为定值;
结论Ⅲ:若,则y的值为4或1.
A.Ⅰ ,Ⅲ均对 B.Ⅱ对,Ⅲ错 C.Ⅱ错,Ⅲ对 D.Ⅰ ,Ⅱ均错
10.如图,将平行四边形沿对角线折叠,使点A落在点E处.若,,则的度数为( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.太阳到地球的距离约为 , 光的速度约为 , 则太阳光从太阳射到地球的时间约为 s.
12.若,则 .
13.因式分解: .
14.如图,将一个周长为厘米的三角形沿射线方向平移后得到三角形,点、、的对应点分别是点、、.连接,已知四边形的周长为厘米,那么平移的距离是 厘米.(用含、的代数式表示结果).
15.如图,点D、E分别为的中点,平分交于点F,若,则 .
16.已知,,则的值为 .
三、计算题(本大题共2题,共20分)
17.(1)计算:;
(2)计算:;
(3)因式分解:.
18.解方程组:
(1)
(2)
四、解答题(本大题共6小题,共46分)
19.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)点A关于y轴对称的点的坐标为______;
(2)把向右平移3个单位,再向下平移4个单位,得到,请在图中画出,点A、B、C的对应点分别是、、.并写出、、的坐标;
(3)求的面积.
20.甲、乙两人共同计算一道整式乘法:,由于甲抄错了第一个多项式中a的符号,得到的结果为;由于乙抄漏了第二个多项式中x的系数,得到的结果为.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
21.如图, 4 个长为 、宽为 的小长方形围成了一个大正方形,请用不同方法计算阴影部分的面积。你能得到怎样的等式?请验证它的正确性。
22.小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示:根据图中的数据(单位:,解答下列问题:
(1)用含、的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多,且地面总面积是卫生间面积的15倍.若铺地砖的平均费用为80元,那么铺地砖的总费用为多少元?
23.阅读理解:
常用的分解因式的方法有提公因式法、公式法,但有很多的多项式只用上述方法就无法分解,如,但我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,如:
. 这种分解因式的方法叫分组分解法.
解决问题:
(1)分解因式:;
(2)三边满足,判断的形状.
24.如图1,直线MN与直线AB、CD分别交于点E、F,∠MEB与∠NFD互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化,若不变,请求出其值;若变化,说明理由.
答案解析部分
1.A
A、∠1和∠2是同旁内角,故本选项错误,符合题意;
B、∠2和∠3是同旁内角,故本选项正确,不符合题意;
C、∠1和∠4是同位角,故本选项正确,不符合题意;
D、∠2和∠4是内错角,故本选项正确,不符合题意;
故答案为:A.
利用同位角,内错角,同旁内角以及对顶角的定义逐项判断解题.
2.C
解:因为
故答案为:C.
用科学记数法表示绝对值较大数字时,常把这个数字表示成的形式,其中,的值取这个数字的位数减。
3.B
解:A:不是等式,故错误;
B:是二元一次方程,故正确;
C:,的次数为,故错误;
D:,含有三个未知数,故错误;
故选:B.
把只含有两个未知数且未知数的次数是1次的整式方程叫二元一次方程.
4.A
解:多项式分解因式后有一个因式是,
当时,多项式的值为,
即,
解得:,
故答案为:.
令时,多项式的值为,求出m值即可.
5.B
解:A. 不能用平方差公式进行计算,故A项符合题意;
B. , 能用平方差公式进行计算,故B项不符合题意;
C. 不能用平方差公式进行计算,故C项不符合题意;
D. 不能用平方差公式进行计算,故D项不符合题意;
故答案为:B.
根据平方差公式:(a+b)(a-b)=a2-b2,即可求得.
6.A
7.D
解:若分配名工人生产电压表,名工人生产电流表,
由题意,得.
故选:D.
本题考查了由实际问题抽象出二元一次方程组,设分配名工人生产电压表,名工人生产电流表,结合电压表数量和电流表数量的等量关系,列出二元一次方程组,即可得到答案.
8.A
9.B
解:由题意可得:,
②-①得:2x=n-m,
解得:,
把代入①得:,
解得:,
∵m+n=8,
∴当n=5时,m=3,
∴,
∴结论Ⅰ正确;
∵①+②得:4x+4y=8,
∴x+y=2,
∴结论Ⅱ正确;
∴当x=1时,y=1,满足 ,
∴m-3n=0,
∴m=3n,
∴m=6,n=2,
∴当x=-2,y=4时,满足,
当x=-1时,则y=3,
∴m=-1+2×3=5,n=-1×3+2×3=3,
∴m-3n=5-3×3=-4,满足,
综上所述:当 时,y的值为4或3或1,
∴结论Ⅲ错误;
故答案为:B.
根据题意先求出,再利用二元一次方程的解,零指数幂和负整数指数幂等计算求解即可。
10.D
解:根据折叠可知,,,
∵四边形为平行四边形,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:D.
根据折叠得出,,根据平行线的性质得出,得出,根据,求出,即可得出,根据三角形内角和定理求出结果即可.
11.
解:∵太阳到地球的距离约为 , 光的速度约为 ,
∴太阳光从太阳射到地球的时间约为:1.5×108÷3.0×105=0.5×103=5×102(s).
故答案为:5×102.
根据单项式除以单项式的法则“系数相除,同底数幂相除 ,只在被除式里的字母则连同它的指数作为积的一个因式“计算即可求解.
12.4.
解:∵a+2b=2,
∴2a+4b=2(a+2b)=2×2=4.
故答案为:4.
先将所求多项式用提公因式法进行因式分解,再整体代入求值即可.
13.
14.
15.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
16.3
解:∵,,
∴,解得:,
则.
故答案为:3.
利用幂的乘方运算性质将原式变形,列出方程组,解方程组即可求得x,y的值,再代入即可求得x-y的值.
17.(1)解:
(2)解:
(3)解:
.
(1)利用幂的乘方法则计算;
(2)利用多项式乘多项式法则计算;
(3)先求出公因式,再利用平方差公式分解因式.
18.(1)解:
把①代入②,得,
解得:,
把代入①,得,
∴方程组的解是.
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
∴方程组的解是.
(1)利用代入消元法的计算方法及步骤分析求解即可;
(2)利用加减消元法的计算方法及步骤分析求解即可.
(1)解:
把①代入②,得,
解得:,
把代入①,得,
所以方程组的解是;
(2)解:,
,得,
解得:,
把代入①,得,
解得:,
所以方程组的解是.
19.(1)
(2)解:△ 如图所示:
由图可得:,,.
(3)解:的面积.
解:
(1),
点关于轴对称的点的坐标为;
故答案为:.
(1)根据关于y轴对称点的坐标变换规律:纵坐标不变,横坐标互为相反相成数求解即可;
(2)利用平移的性质:图形的平移即对应的点平移,因此可将点A、B、C 向右平移3个单位,再向下平移4个单位,得到、、 作出图形,再根据点的位置,写出坐标即可;
(3)利用网格,根据的面积=55的正方形面积减去三个直角三角形面积计算即可.
(1)解:,
点关于轴对称的点的坐标为.
故答案为:.
(2)解:△ 如图所示,
由图可得:,,.
(3)解:的面积.
20.,正确结果为
21.解:方法一:S阴影=(a+b)2-(a-b)2;方法二:S阴影=4ab;
∴可得等式:(a+b)2-(a-b)2=4ab;
证明:(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=4ab.
利用不同的表达式表示阴影部分的面积可得等式(a+b)2-(a-b)2=4ab;再利用完全平方公式的计算方法分析求解即可.
22.(1)解:地面总面积为:
(2)解:由题意得,解得:,
地面总面积为:,
铺地砖的总费用为:(元.
答:铺地砖的总费用为3600元.
(1)由图形可得:客厅的长为6,宽为x,厨房的长为3,宽为2,卫生间的长为2,宽为y,卧室的长为3,宽为4,然后根据矩形的面积公式进行解答;
(2)根据客厅面积比卫生间面积多21m2可得6x-2y=21,根据地面总面积是卫生间面积的15倍可得另一个x与y的方程,联立求出x、y的值,代入(1)的结果中求出地面的总面积,再乘以每平方米的费用即可求出总费用.
23.(1)
(2)等腰三角形
24.(1)解:如图1,AB∥CD,理由如下:
∵ ∠MEB与∠NFD互补 ,
∴∠MEB+∠NFD=180°,
又∵∠MEB=∠AEF,∠NFD=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)证明:如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°,
又∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵GH⊥EG,
∴PF∥GH;
(3)解:∠HPQ的大小不会发生变化,理由如下:
∵∠PHK=∠HPK
∴∠PKG=2∠HPK
∵GH⊥EG
∴∠KPG=90°-∠PKG=90°-2∠HPK
∴∠EPK=180°-∠KPG=90°+2∠HPK
∵PQ平分∠EPK
∴∠QPK=∠EPK=45°+∠HPK
∴∠HPQ=∠QPK-∠HPK=45°
∴∠HPQ的大小不会发生变化,其值为45°.
(1)根据补角的定义得∠MEB+∠NFD=180°,根据对顶角相等得∠MEB=∠AEF,∠NFD=∠CFE,从而可得∠AEF+∠CFE=180°,由同旁内角互补,两直线平行,得出结论AB∥CD;
(2)根据二直线平行,同旁内角互补得∠BEF+∠EFD=180°,根据角平分线的定义得∠FEP+∠EFP=(∠BEF+∠EFD)=90°,根据三角形的内角和定理得∠EPF=90°,即EG⊥PF,进而根据同一平面内垂直同一直线的两条直线互相平行可得PF∥GH;
(3)∠HPQ的大小不会发生变化,理由如下:根据三角形外角性质并结合∠PHK=∠HPK得∠PKG=2∠HPK,利用三角形外角定理、三角形内角和定理求得∠KPG=90° ∠PKG=90° 2∠HPK;再由邻补角的定义、角平分线的定义推得∠QPK=12∠EPK=45°+∠HPK;然后由图形中角与角的和差关系求得∠HPQ=45°即可.
同课章节目录
