2024-2025学年七年级下学期数学期中考试(瑞安市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中考试(瑞安市专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 09:41:36 | ||
图片预览


文档简介
保密★启用前
2024-2025学年七年级下册期中考试(瑞安市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选,多选,错选均不给分)
1.下列命题中,假命题的是( )
A.两直线平行,同旁内角互补
B.等角的补角相等
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.内错角相等
2.下列运动中不属于旋转的是( )
A.摩天轮的转动 B.酒店旋转门的转动
C.气球升空的运动 D.电风扇叶片的转动
3.随着我国科技迅猛发展,中国在芯片制造技术领域取得了显著的进步,成功自研出达到5纳米()工艺制造技术的手机芯片.已知,将数据0.000000005用科学记数法表示是( )
A. B. C. D.
4.已知是方程的解,则m的值为( )
A. B.7 C.3 D.9
5.下列计算正确的是( )
A. B. C. D.
6.下列运算中正确的是( )
A. B.
C. D.
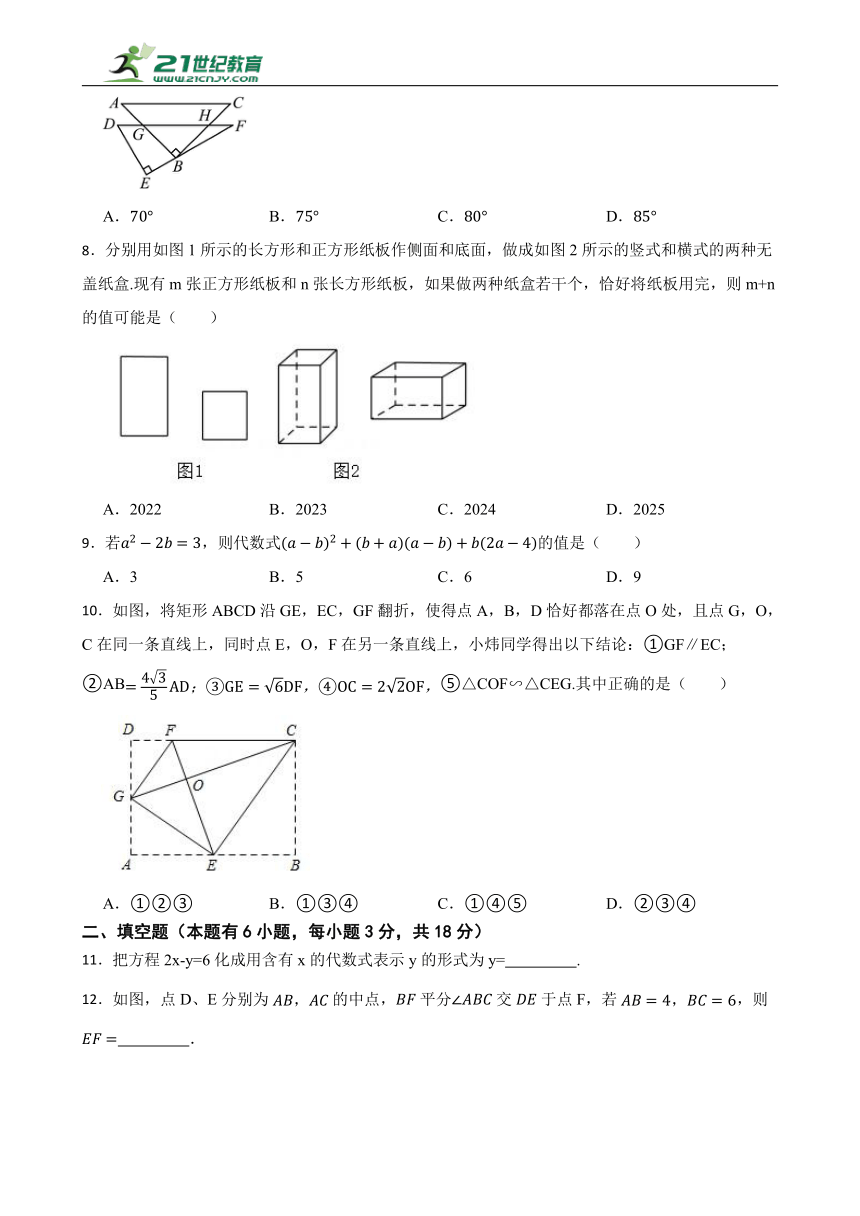
7.两个直角三角板如图所示摆放,其中,点B在边上,分别与交于点G,H,若,则的大小为( )
A. B. C. D.
8.分别用如图1所示的长方形和正方形纸板作侧面和底面,做成如图2所示的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.2022 B.2023 C.2024 D.2025
9.若,则代数式的值是( )
A.3 B.5 C.6 D.9
10.如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( )
A.①②③ B.①③④ C.①④⑤ D.②③④
二、填空题(本题有6小题,每小题3分,共18分)
11.把方程2x-y=6化成用含有x的代数式表示y的形式为y= .
12.如图,点D、E分别为的中点,平分交于点F,若,则 .
13. 计算:
14.如图,直角三角形ABC的周长为2024,在其内部有5个小直角三角形,且这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形的周长之和是 。
15.已知是方程组的解,则的算术平方根为 .
16.如图, 两个正方形边长分别为 , .如果 , 那么阴影部分的面积为
三、解答题(本题有7小题,共52分)
17.计算:
(1)
(2)
(3)用简便方法计算:
(4).
18.解下列方程组:
(1);
(2);
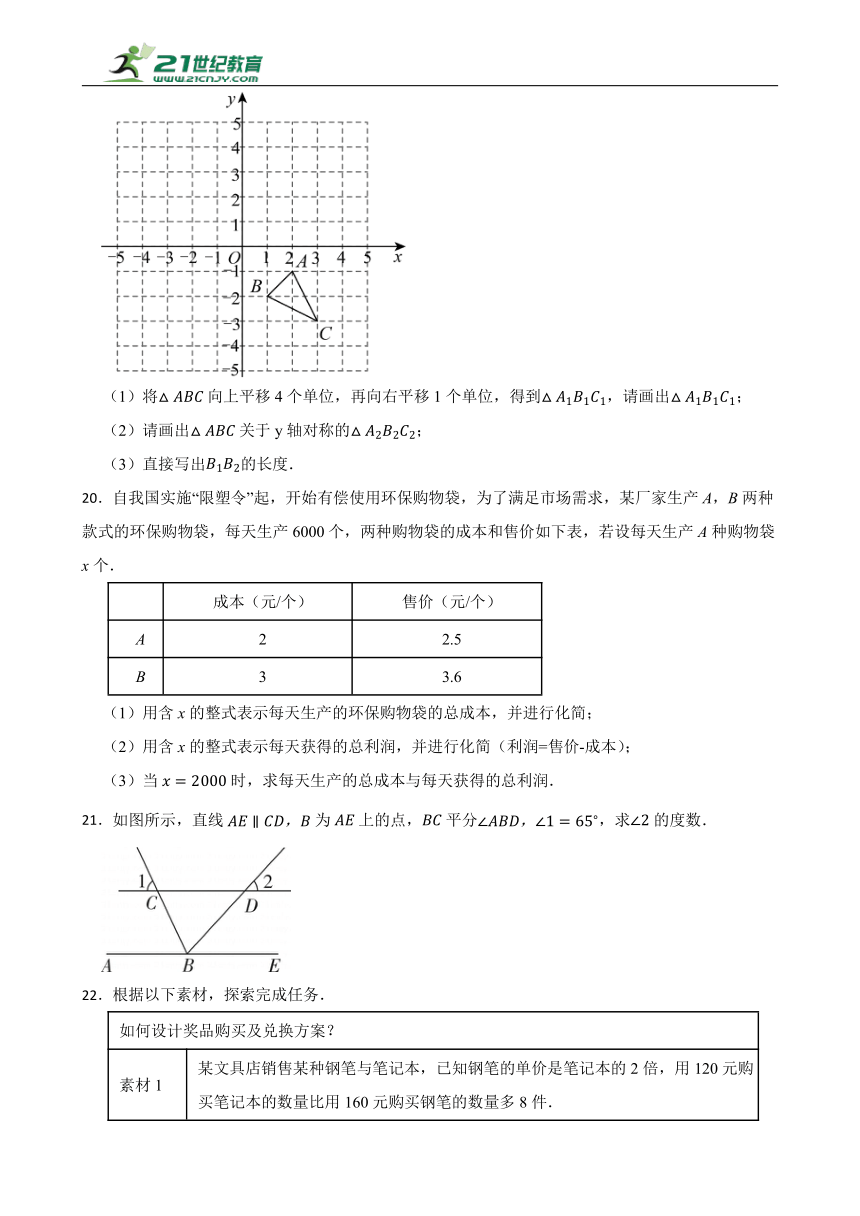
19.如图,在平面直角坐标系中,已知的三个顶点坐标分别是.
(1)将向上平移4个单位,再向右平移1个单位,得到,请画出;
(2)请画出关于y轴对称的;
(3)直接写出的长度.
20.自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A,B两种款式的环保购物袋,每天生产6000个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋x个.
成本(元/个) 售价(元/个)
A 2 2.5
B 3 3.6
(1)用含x的整式表示每天生产的环保购物袋的总成本,并进行化简;
(2)用含x的整式表示每天获得的总利润,并进行化简(利润=售价-成本);
(3)当时,求每天生产的总成本与每天获得的总利润.
21.如图所示,直线为上的点,平分,求的度数.
22.根据以下素材,探索完成任务.
如何设计奖品购买及兑换方案?
素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的2倍,用120元购买笔记本的数量比用160元购买钢笔的数量多8件.
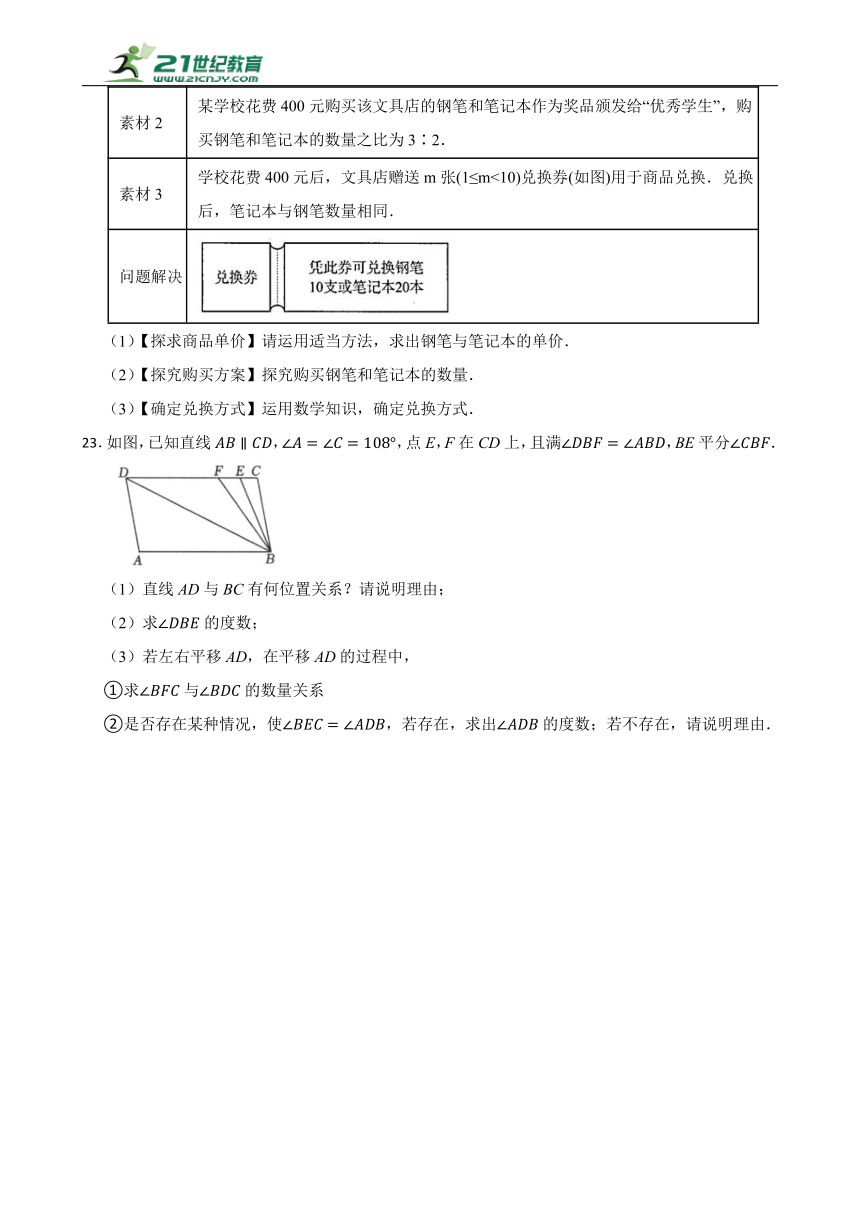
素材2 某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”,购买钢笔和笔记本的数量之比为3∶2.
素材3 学校花费400元后,文具店赠送m张(1≤m<10)兑换券(如图)用于商品兑换.兑换后,笔记本与钢笔数量相同.
问题解决
(1)【探求商品单价】请运用适当方法,求出钢笔与笔记本的单价.
(2)【探究购买方案】探究购买钢笔和笔记本的数量.
(3)【确定兑换方式】运用数学知识,确定兑换方式.
23.如图,已知直线,,点E,F在CD上,且满,BE平分.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求的度数;
(3)若左右平移AD,在平移AD的过程中,
①求与的数量关系
②是否存在某种情况,使,若存在,求出的度数;若不存在,请说明理由.
答案解析部分
1.D
解:A中,两直线平行,同旁内角才互补,所以A是真命题;
B中,等角的补角相等,所以B是真命题;
C中,在同一平面内,过一点有且只有一条直线与已知直线垂直,所以C是真命题;
D中,两直线平行,内错角相等,所以D是假命题;
故选:D.
本题主要考查命题的判定,根据两直线的位置关系,平行线的性质,补角的定义,结合选项,逐一判断,即可得到答案.
2.C
3.B
4.D
解:∵是方程的解,
∴,
解得:.
故选:D.
本题考查二元一次方程的解,其中方程的解即为能使方程左右两边相等的未知数的值,将x和y的值,代入原方程,得到关于的一元一次方程,求得方程的解,即可得到答案.
5.C
解:A.a3·a2=a5,故A不符合题意;
B. , 故B不符合题意;
C.,故C符合题意;
D.,故D不符合题意.
故答案为:C.
根据同底数幂的除法,合并同类项,同底数幂的乘法,幂的乘方与积的乘方法则,进行计算逐一判断即可解答.
6.B
7.B
解:∵,,
∴,
∵,,
∴,
∴,
∴的大小为.
故答案为:B
先根据平行线的性质(同位角)得到,进而根据三角形内角和得到∠F的度数,则.
8.D
解:设可以做竖式纸盒x个,横式纸盒y个,
∴
∵x和y均为整数,则m为5的倍数,
故答案为:D.
根据图2知,做一个竖式纸盒需要正方形纸板1个,长方形纸板4个;做一个横式纸盒需要正方形纸板2个,长方形纸板3个,设可以做竖式纸盒x个,横式纸盒y个,根据题干列出方程,即可求解.
9.C
解:
,
∵
∴原式,
故答案为:C.
先利用平方差以及完全平方公式化简代数式,然后利用整体代入求值即可.
10.B
解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,
∠DGF=∠FGO,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,
∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,
∴∠FGE+∠GEC=180°,
∴GF∥CE,①正确;
设AD=2a,AB=2b,
则DG=OG=AG=a,AE=OE=BE=b,
∴CG=OG+OC=3a,
在Rt△AGE中,GE2=AG2+AE2=a2+b2,
在Rt△CGE中,CE2=BE2+CB2=b2+(2a)2,
在Rt△CGE中,CG2=GE2+CE2,
即(3a)2=a2+b2+b2+(2a)2,
解得:;
∴;②错误;
设OF=DF=x,则,
在Rt△COF中,CF2=OF2+OC2,
∴,
解得:;
∴,,
在Rt△AGE中,,
∴,;③④正确;
根据题意,无法得出∠FCO=∠GCE,
∴无法判断△COF∽△CEG;⑤错误;
综上,正确的是①③④,
故答案为:B.
根据折叠前后图形的对应边和对应角相等可推得∠FGE+∠GEC=180°,根据同旁内角互补,两直线平行即可得出GF∥CE,判断①正确,设AD=2a,AB=2b,求得CG=3a,根据直角三角形中两直角边的平方和等于斜边的平方可求得,即可求得AB与AD的数量关系,判断②错误,设OF=DF=x,求得CF的值,根据直角三角形中两直角边的平方和等于斜边的平方得出x与a的关系式,GE的值,即可判断③④正确,结合题意无法得出△COF∽△CEG;判断⑤错误,即可得出答案.
11.2x-6
解:2x-y=6
移项,得2x-6=y,即y=2x-6.
故答案为:2x-6.
将含y的项移到方程的右一边,其它的项留在方程的左边,最后根据等式性质,两边同时交换即可.
12.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
13.1
解:
=
=
=
=
=1,
故答案为:1.
利用积的乘方的逆运算方法(把积的每一个因式分别乘方,再把所得的幂相乘)分析求解即可.
14.2024
解:∵这5个小直角三角形都有一条边与BC平行,
∴这5个小直角三角形都有一条边与AC平行,
∴这5个小直角三角形的周长之和等于直角三角形ABC的周长2024,
故答案为:2024.
根据题意得到这5个小直角三角形都有一条边与AC平行,则小直角三角形中与AC平行的边之和等于AC,与BC平行的边的和等于BC,进而即可求解.
15.
16.144
解:如图所示:
根据题意可得:AB=AD=BC=a,EF=EC=GF=b,,
∴S阴影=S正方形ABCD+S正方形ECGF-S△ABD-S△BGF
=a2+b2-a2-(a+b)b
=a2+b2-a2-ab-b2
=(a2+b2-ab)
=[(a+b)2-3ab]
=×(182-3×12)
=×288
=144,
故答案为:144.
利用正方形的面积公式、三角形的面积公式列出算式,再利用割补法求出阴影部分的面积即可.
17.(1)
(2)
(3)
(4)
18.(1)
(2)
19.(1)解:如图所示,即为所示;
(2)解:如图所示,即为所求;
(3)解:由题意知,,,
∴,
∴
(1)由平移规律先确定A1,B1,C1的坐标,再描点,连线即可;
(2)由轴对称的性质先确定A2,B2,C2的坐标,再描点连线即可;
(3)根据两点坐标,然后利用勾股定理求解即可.
(1)解:如图所示,即为所示;
(2)解:如图所示,即为所求;
(3)解:由题意知,,,
∴,
∴
20.(1)解:每天生产A种购物袋x个,则每天生产B种购物袋个.
元.每天生产的环保购物袋的总成本为元;
(2)解:元,
每天获得的总利润为元;
(3)解:当时,(元),
(元),
当时,每天生产的总成本为16000元,每天获得的总利润为3400元.
(1)根据成本=成本单价×购物袋的个数,分别表示A、B两款购物袋的成本求和化简即可;
(2)根据利润=售价-成本的计算方法,分别求出A、B两款购物袋的利润再求和;
(3)把x=2000代入计算即可.
21.解:,
22.(1)解:设笔记本的单价为x元,则钢笔的单价为2x元,根据题意得:
解得:x=5,
经检验,x=5是原方程的根,且符合题意.
∴2x=10 (元),
答:笔记本的单价为5元,钢笔的单价为10元.
(2)解:设购买钢笔的数量为a支,笔记本数量为b支,根据题意得:
解得:
答:购买钢笔的数量为30支,笔记本数量为20支.
(3)解:当购买钢笔的数量为30支,笔记本数量为20支时,设有a张兑换券兑换钢笔,则有( m-a )张兑换券兑换笔记本,根据题意得:
30+10a=20+20×( m-a),
整理得:
∵1≤m<10,
∴
∵m,a均为正整数,
∴3a+1为偶数(2的倍数),
∴a可取1,3,5.
当a=1时,m=2,则30+10=20+20×(2-1) ,成立;
当a=3时,m=5,则30+10×3=20+20×(5-3),成立;
当a=5时,m=8,则30+10×5=20+20×(8-5),成立;
根据题意可知,
当a=3时,赠送的总价为3×10×10+(5-3)×5×20=500元;
当a=5时,赠送的总价为5×10×10+(8-5)×5×20=800元;
赠送的总价比出的钱还多,不合理,
∴文具店赠送2张兑换券,其中有1张兑换券兑换钢笔,有1张兑换券兑换笔记本.
答:文具店赠送2张兑换券,其中有I张兑换券兑换钢笔,有1张兑换券兑换笔记本.
(1)根据题意得等量关系: 钢笔的单价=笔记本的单价×2,用120元购买笔记本的数量=用160元购买钢笔的数量+8,设笔记本的单价为x元,则钢笔的单价为2x元,代入等量关系列方程求解即可,注意检验.
(2)根据题意得等量关系:10×购买钢笔的数量+5×购买笔记本的数量=400;购买钢笔的数量:购买笔记本的数量=3:2,设购买钢笔的数量为a支,笔记本数量为b支,代入得方程,求解即可.
(3)设有a张兑换券兑换钢笔,则有( m-a )张兑换券兑换笔记本,根据题意得:30+10a=20+20× ( m-a),整理得,根据m的取值范围分类讨论即可.
23.(1)解:直线AD与BC互相平行,理由:
∵,
∴,
又∵
∴,
∴;
(2)解:∵;
∴,
∵,BE平分,
∴;
(3)解:①∵
∴,
∵,
∴
∴
②存在,理由如下:
设.
∵,
∴;
,
∴,
当时,,
∴
∴,
即
(1)利用平行线的性质可得,再结合利用等量代换可得,从而可证出;
(2)先利用平行线的性质及角的运算求出,再利用角平分线的定义及等量代换可得;
(3)①利用平行线的性质可得,,再利用角的运算和等量代换可得;②设,利用平行线的性质及角的运算求出,再结合可得,求出x的值,最后求出,即即可.
2024-2025学年七年级下册期中考试(瑞安市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选,多选,错选均不给分)
1.下列命题中,假命题的是( )
A.两直线平行,同旁内角互补
B.等角的补角相等
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.内错角相等
2.下列运动中不属于旋转的是( )
A.摩天轮的转动 B.酒店旋转门的转动
C.气球升空的运动 D.电风扇叶片的转动
3.随着我国科技迅猛发展,中国在芯片制造技术领域取得了显著的进步,成功自研出达到5纳米()工艺制造技术的手机芯片.已知,将数据0.000000005用科学记数法表示是( )
A. B. C. D.
4.已知是方程的解,则m的值为( )
A. B.7 C.3 D.9
5.下列计算正确的是( )
A. B. C. D.
6.下列运算中正确的是( )
A. B.
C. D.
7.两个直角三角板如图所示摆放,其中,点B在边上,分别与交于点G,H,若,则的大小为( )
A. B. C. D.
8.分别用如图1所示的长方形和正方形纸板作侧面和底面,做成如图2所示的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.2022 B.2023 C.2024 D.2025
9.若,则代数式的值是( )
A.3 B.5 C.6 D.9
10.如图,将矩形ABCD沿GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,同时点E,O,F在另一条直线上,小炜同学得出以下结论:①GF∥EC;②AB⑤△COF∽△CEG.其中正确的是( )
A.①②③ B.①③④ C.①④⑤ D.②③④
二、填空题(本题有6小题,每小题3分,共18分)
11.把方程2x-y=6化成用含有x的代数式表示y的形式为y= .
12.如图,点D、E分别为的中点,平分交于点F,若,则 .
13. 计算:
14.如图,直角三角形ABC的周长为2024,在其内部有5个小直角三角形,且这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形的周长之和是 。
15.已知是方程组的解,则的算术平方根为 .
16.如图, 两个正方形边长分别为 , .如果 , 那么阴影部分的面积为
三、解答题(本题有7小题,共52分)
17.计算:
(1)
(2)
(3)用简便方法计算:
(4).
18.解下列方程组:
(1);
(2);
19.如图,在平面直角坐标系中,已知的三个顶点坐标分别是.
(1)将向上平移4个单位,再向右平移1个单位,得到,请画出;
(2)请画出关于y轴对称的;
(3)直接写出的长度.
20.自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A,B两种款式的环保购物袋,每天生产6000个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋x个.
成本(元/个) 售价(元/个)
A 2 2.5
B 3 3.6
(1)用含x的整式表示每天生产的环保购物袋的总成本,并进行化简;
(2)用含x的整式表示每天获得的总利润,并进行化简(利润=售价-成本);
(3)当时,求每天生产的总成本与每天获得的总利润.
21.如图所示,直线为上的点,平分,求的度数.
22.根据以下素材,探索完成任务.
如何设计奖品购买及兑换方案?
素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的2倍,用120元购买笔记本的数量比用160元购买钢笔的数量多8件.
素材2 某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”,购买钢笔和笔记本的数量之比为3∶2.
素材3 学校花费400元后,文具店赠送m张(1≤m<10)兑换券(如图)用于商品兑换.兑换后,笔记本与钢笔数量相同.
问题解决
(1)【探求商品单价】请运用适当方法,求出钢笔与笔记本的单价.
(2)【探究购买方案】探究购买钢笔和笔记本的数量.
(3)【确定兑换方式】运用数学知识,确定兑换方式.
23.如图,已知直线,,点E,F在CD上,且满,BE平分.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求的度数;
(3)若左右平移AD,在平移AD的过程中,
①求与的数量关系
②是否存在某种情况,使,若存在,求出的度数;若不存在,请说明理由.
答案解析部分
1.D
解:A中,两直线平行,同旁内角才互补,所以A是真命题;
B中,等角的补角相等,所以B是真命题;
C中,在同一平面内,过一点有且只有一条直线与已知直线垂直,所以C是真命题;
D中,两直线平行,内错角相等,所以D是假命题;
故选:D.
本题主要考查命题的判定,根据两直线的位置关系,平行线的性质,补角的定义,结合选项,逐一判断,即可得到答案.
2.C
3.B
4.D
解:∵是方程的解,
∴,
解得:.
故选:D.
本题考查二元一次方程的解,其中方程的解即为能使方程左右两边相等的未知数的值,将x和y的值,代入原方程,得到关于的一元一次方程,求得方程的解,即可得到答案.
5.C
解:A.a3·a2=a5,故A不符合题意;
B. , 故B不符合题意;
C.,故C符合题意;
D.,故D不符合题意.
故答案为:C.
根据同底数幂的除法,合并同类项,同底数幂的乘法,幂的乘方与积的乘方法则,进行计算逐一判断即可解答.
6.B
7.B
解:∵,,
∴,
∵,,
∴,
∴,
∴的大小为.
故答案为:B
先根据平行线的性质(同位角)得到,进而根据三角形内角和得到∠F的度数,则.
8.D
解:设可以做竖式纸盒x个,横式纸盒y个,
∴
∵x和y均为整数,则m为5的倍数,
故答案为:D.
根据图2知,做一个竖式纸盒需要正方形纸板1个,长方形纸板4个;做一个横式纸盒需要正方形纸板2个,长方形纸板3个,设可以做竖式纸盒x个,横式纸盒y个,根据题干列出方程,即可求解.
9.C
解:
,
∵
∴原式,
故答案为:C.
先利用平方差以及完全平方公式化简代数式,然后利用整体代入求值即可.
10.B
解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,
∠DGF=∠FGO,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,
∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,
∴∠FGE+∠GEC=180°,
∴GF∥CE,①正确;
设AD=2a,AB=2b,
则DG=OG=AG=a,AE=OE=BE=b,
∴CG=OG+OC=3a,
在Rt△AGE中,GE2=AG2+AE2=a2+b2,
在Rt△CGE中,CE2=BE2+CB2=b2+(2a)2,
在Rt△CGE中,CG2=GE2+CE2,
即(3a)2=a2+b2+b2+(2a)2,
解得:;
∴;②错误;
设OF=DF=x,则,
在Rt△COF中,CF2=OF2+OC2,
∴,
解得:;
∴,,
在Rt△AGE中,,
∴,;③④正确;
根据题意,无法得出∠FCO=∠GCE,
∴无法判断△COF∽△CEG;⑤错误;
综上,正确的是①③④,
故答案为:B.
根据折叠前后图形的对应边和对应角相等可推得∠FGE+∠GEC=180°,根据同旁内角互补,两直线平行即可得出GF∥CE,判断①正确,设AD=2a,AB=2b,求得CG=3a,根据直角三角形中两直角边的平方和等于斜边的平方可求得,即可求得AB与AD的数量关系,判断②错误,设OF=DF=x,求得CF的值,根据直角三角形中两直角边的平方和等于斜边的平方得出x与a的关系式,GE的值,即可判断③④正确,结合题意无法得出△COF∽△CEG;判断⑤错误,即可得出答案.
11.2x-6
解:2x-y=6
移项,得2x-6=y,即y=2x-6.
故答案为:2x-6.
将含y的项移到方程的右一边,其它的项留在方程的左边,最后根据等式性质,两边同时交换即可.
12.1
解:∵点D、E分别为的中点,,
∴是的中位线,,
∴,,
∴,
∵平分交于点F,
∴,
∴,
∴,
∴,
故答案为:1.
利用三角形中位线性质得到,,利用中点定义得到,再利用平行线的性质和角平分线得到,则,即可得到的长度.
13.1
解:
=
=
=
=
=1,
故答案为:1.
利用积的乘方的逆运算方法(把积的每一个因式分别乘方,再把所得的幂相乘)分析求解即可.
14.2024
解:∵这5个小直角三角形都有一条边与BC平行,
∴这5个小直角三角形都有一条边与AC平行,
∴这5个小直角三角形的周长之和等于直角三角形ABC的周长2024,
故答案为:2024.
根据题意得到这5个小直角三角形都有一条边与AC平行,则小直角三角形中与AC平行的边之和等于AC,与BC平行的边的和等于BC,进而即可求解.
15.
16.144
解:如图所示:
根据题意可得:AB=AD=BC=a,EF=EC=GF=b,,
∴S阴影=S正方形ABCD+S正方形ECGF-S△ABD-S△BGF
=a2+b2-a2-(a+b)b
=a2+b2-a2-ab-b2
=(a2+b2-ab)
=[(a+b)2-3ab]
=×(182-3×12)
=×288
=144,
故答案为:144.
利用正方形的面积公式、三角形的面积公式列出算式,再利用割补法求出阴影部分的面积即可.
17.(1)
(2)
(3)
(4)
18.(1)
(2)
19.(1)解:如图所示,即为所示;
(2)解:如图所示,即为所求;
(3)解:由题意知,,,
∴,
∴
(1)由平移规律先确定A1,B1,C1的坐标,再描点,连线即可;
(2)由轴对称的性质先确定A2,B2,C2的坐标,再描点连线即可;
(3)根据两点坐标,然后利用勾股定理求解即可.
(1)解:如图所示,即为所示;
(2)解:如图所示,即为所求;
(3)解:由题意知,,,
∴,
∴
20.(1)解:每天生产A种购物袋x个,则每天生产B种购物袋个.
元.每天生产的环保购物袋的总成本为元;
(2)解:元,
每天获得的总利润为元;
(3)解:当时,(元),
(元),
当时,每天生产的总成本为16000元,每天获得的总利润为3400元.
(1)根据成本=成本单价×购物袋的个数,分别表示A、B两款购物袋的成本求和化简即可;
(2)根据利润=售价-成本的计算方法,分别求出A、B两款购物袋的利润再求和;
(3)把x=2000代入计算即可.
21.解:,
22.(1)解:设笔记本的单价为x元,则钢笔的单价为2x元,根据题意得:
解得:x=5,
经检验,x=5是原方程的根,且符合题意.
∴2x=10 (元),
答:笔记本的单价为5元,钢笔的单价为10元.
(2)解:设购买钢笔的数量为a支,笔记本数量为b支,根据题意得:
解得:
答:购买钢笔的数量为30支,笔记本数量为20支.
(3)解:当购买钢笔的数量为30支,笔记本数量为20支时,设有a张兑换券兑换钢笔,则有( m-a )张兑换券兑换笔记本,根据题意得:
30+10a=20+20×( m-a),
整理得:
∵1≤m<10,
∴
∵m,a均为正整数,
∴3a+1为偶数(2的倍数),
∴a可取1,3,5.
当a=1时,m=2,则30+10=20+20×(2-1) ,成立;
当a=3时,m=5,则30+10×3=20+20×(5-3),成立;
当a=5时,m=8,则30+10×5=20+20×(8-5),成立;
根据题意可知,
当a=3时,赠送的总价为3×10×10+(5-3)×5×20=500元;
当a=5时,赠送的总价为5×10×10+(8-5)×5×20=800元;
赠送的总价比出的钱还多,不合理,
∴文具店赠送2张兑换券,其中有1张兑换券兑换钢笔,有1张兑换券兑换笔记本.
答:文具店赠送2张兑换券,其中有I张兑换券兑换钢笔,有1张兑换券兑换笔记本.
(1)根据题意得等量关系: 钢笔的单价=笔记本的单价×2,用120元购买笔记本的数量=用160元购买钢笔的数量+8,设笔记本的单价为x元,则钢笔的单价为2x元,代入等量关系列方程求解即可,注意检验.
(2)根据题意得等量关系:10×购买钢笔的数量+5×购买笔记本的数量=400;购买钢笔的数量:购买笔记本的数量=3:2,设购买钢笔的数量为a支,笔记本数量为b支,代入得方程,求解即可.
(3)设有a张兑换券兑换钢笔,则有( m-a )张兑换券兑换笔记本,根据题意得:30+10a=20+20× ( m-a),整理得,根据m的取值范围分类讨论即可.
23.(1)解:直线AD与BC互相平行,理由:
∵,
∴,
又∵
∴,
∴;
(2)解:∵;
∴,
∵,BE平分,
∴;
(3)解:①∵
∴,
∵,
∴
∴
②存在,理由如下:
设.
∵,
∴;
,
∴,
当时,,
∴
∴,
即
(1)利用平行线的性质可得,再结合利用等量代换可得,从而可证出;
(2)先利用平行线的性质及角的运算求出,再利用角平分线的定义及等量代换可得;
(3)①利用平行线的性质可得,,再利用角的运算和等量代换可得;②设,利用平行线的性质及角的运算求出,再结合可得,求出x的值,最后求出,即即可.
同课章节目录
