2024-2025学年七年级下学期数学(浙教版)期中考试(答案+解析)
文档属性
| 名称 | 2024-2025学年七年级下学期数学(浙教版)期中考试(答案+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 448.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览


文档简介
保密★启用前
2024-2025学年七年级下册期中考试(浙教版专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共10小题,每题3分, 共30分.)
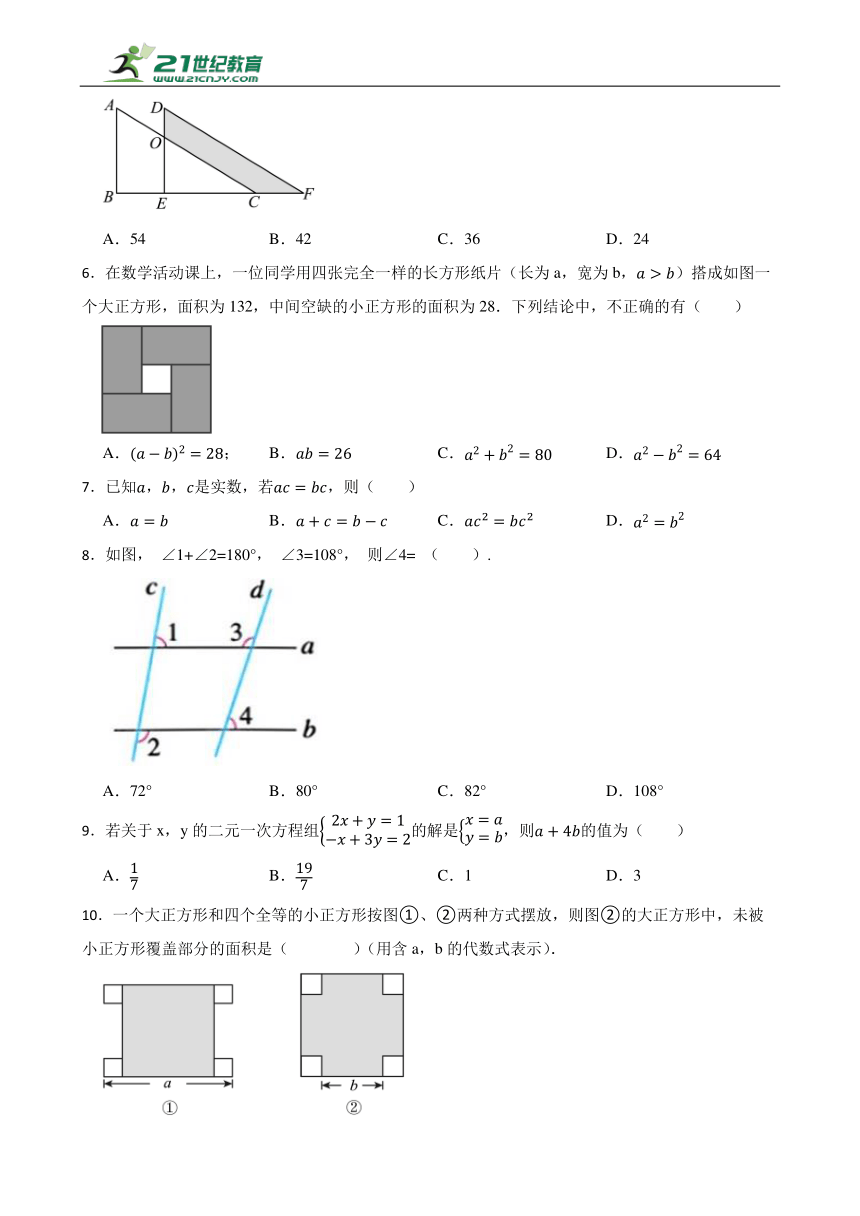
1.如图,沿路线行走,若,,则( )
A. B. C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,大正方形的边长为m,小正方形的边长为n,x,y表示四个相同长方形的两边长.则①;②;③;④中,正确的是( )
A.①③④ B.②④ C.①③ D.①②③④
4.若方程组的解x、y 的值相等,则a的值为( )
A.2 B.4 C. D.1
5.如图,将沿着点到的方向平移到的位置,,,平移距离为6,则阴影部分面积为( )
A.54 B.42 C.36 D.24
6.在数学活动课上,一位同学用四张完全一样的长方形纸片(长为a,宽为b,)搭成如图一个大正方形,面积为132,中间空缺的小正方形的面积为28.下列结论中,不正确的有( )
A.; B. C. D.
7.已知,,是实数,若,则( )
A. B. C. D.
8.如图, ∠1+∠2=180°, ∠3=108°, 则∠4= ( ).
A.72° B.80° C.82° D.108°
9.若关于x,y的二元一次方程组的解是,则的值为( )
A. B. C.1 D.3
10.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
A.ab B.2ab C.a2﹣ab D.b2+ab
二、填空题(共6小题,每题3分, 共18分.)
11.对于实数a,b,我们定义符号的意义为:当时,;当时,.如:,则关于的函数为的最大值是 .
12.定义:如果一个数的平方等于,记为,那么这个数叫做虚数单位,把形如(a,b为实数)的数叫做复数,其中a叫做这个复数的实部,叫做这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:.
根据以上信息,下列各式:
①;
②;
③
④.
其中正确的是 (填上所有正确答案的序号).
13.已知代数式,则代数式的值是 .
14.射线,,,是同一平面内互不重合的四条射线,,,,则的度数为 .
15.如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D'、C'的位置处,若∠1=56°,则∠EFB的度数是 .
16.如果a,b都是有理数,且满足,则的值为 .
三、解答题(本大题有7个小题,共72分. 解答应写出文字说明、证明过程或演算步骤.)
17.已知关于x、y的方程组
(1)求x与y的关系式(用只含x的代数式表示y).
(2)若x、y的解满足x-y=-3,求a的值.
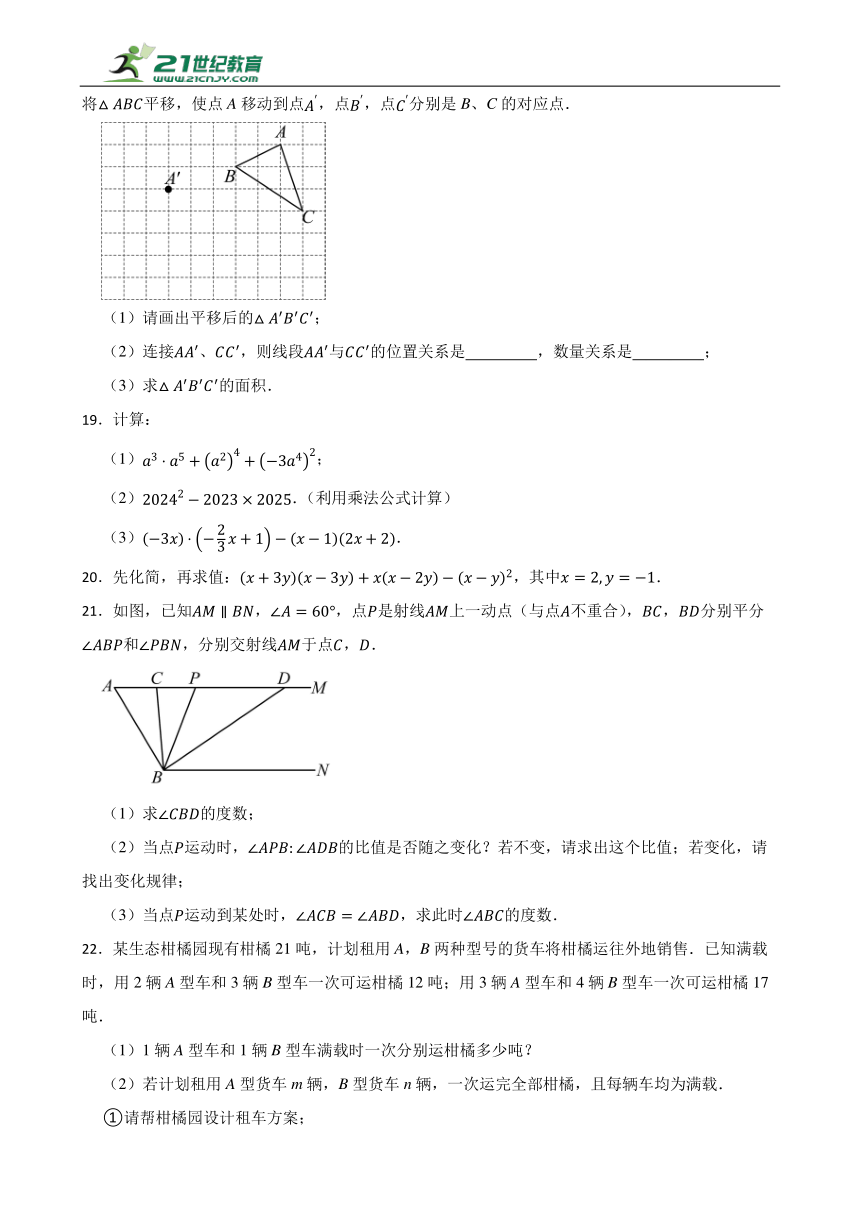
18.在正方形网格中,每个小正方形的边长均为1个单位长度,三个顶点的位置如图所示,现将平移,使点A移动到点,点,点分别是B、C的对应点.
(1)请画出平移后的;
(2)连接、,则线段与的位置关系是 ,数量关系是 ;
(3)求的面积.
19.计算:
(1);
(2).(利用乘法公式计算)
(3).
20.先化简,再求值:,其中.
21.如图,已知,,点是射线上一动点(与点不重合),,分别平分和,分别交射线于点,.
(1)求的度数;
(2)当点运动时,的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点运动到某处时,,求此时的度数.
22.某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.
(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;
②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
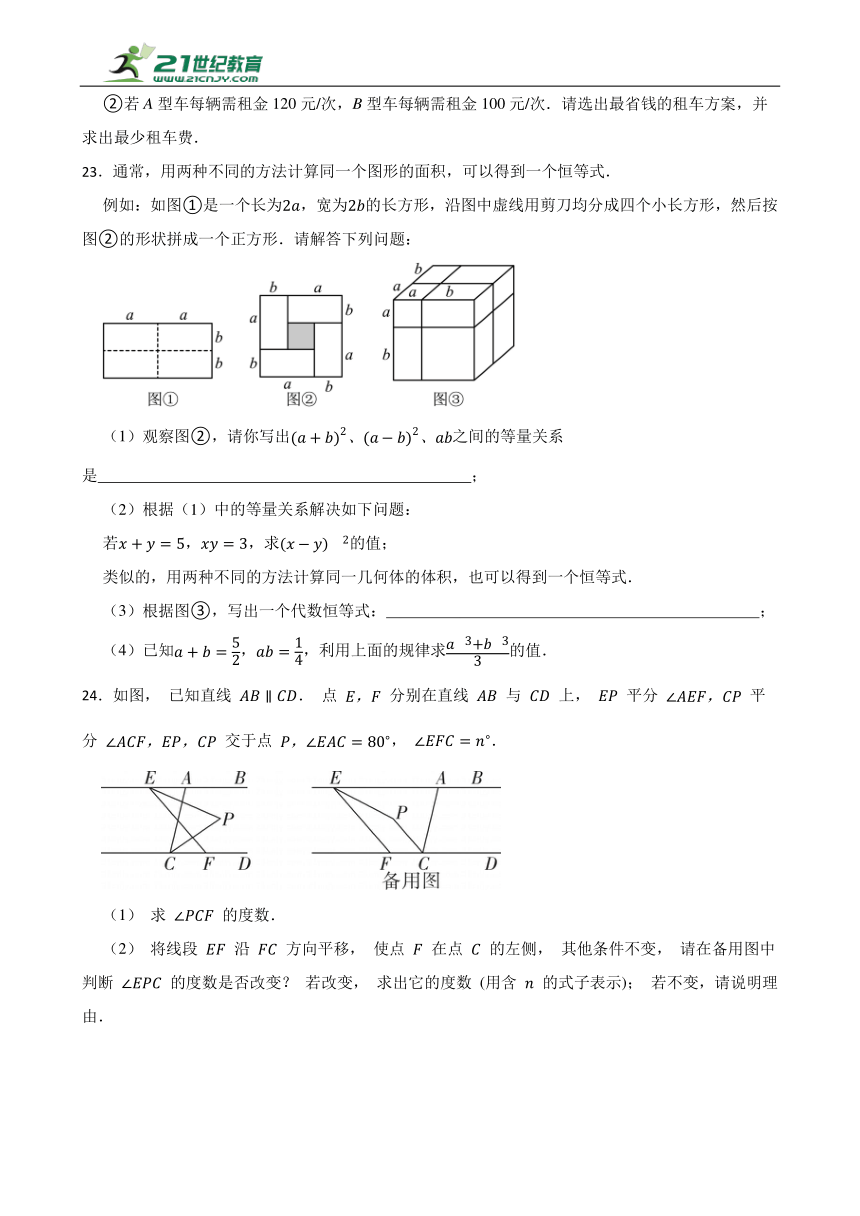
23.通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
(1)观察图②,请你写出之间的等量关系是 ;
(2)根据(1)中的等量关系解决如下问题:
若,,求的值;
类似的,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(3)根据图③,写出一个代数恒等式: ;
(4)已知,,利用上面的规律求的值.
24.如图, 已知直线 . 点 分别在直线 与 上, 平分 平分 交于点 , .
(1) 求 的度数.
(2) 将线段 沿 方向平移, 使点 在点 的左侧, 其他条件不变, 请在备用图中判断 的度数是否改变? 若改变, 求出它的度数 (用含 的式子表示); 若不变,请说明理由.
答案解析部分
1.B
2.C
3.D
解:①由图得,故①正确;
②由图得
,
,
,
故②正确;
③由图得
,
,
,
;
故③正确;
④由得,
,
,
,
,
;
故④正确;
故答案为:D.
根据边长关系判断①;根据判断 ② ;根据平方差公式判断③ ;根据完全平方公式的变形判断④解题.
4.A
5.B
6.D
解:由拼图可得,大正方形的边长为,中间的小正方形的边长为,
∴,,
故选项A正确,不符合题意;
∵,,
∴,
∴,,
故选项B,C正确,不符合题意;
∵,,
∴,
∵,
∴,
故选项D错误,符合题意.
故答案为:D.
根据拼图得出,,,由②可判断A;①-②可求得ab的值,进而可判断B;算式①结合ab的值可求得a2+b2,进而可判断C;①×②再开方可得a2-b2,进而可判断D.
7.C
解:A、无法证明c是否为0,则本项不一定正确;
B、等式左边为加,右边为减,则本项错误;
C、∵则本项正确;
D、无法判断该项的正确性;
故答案为:C.
根据等式的基本性质:等式两边同时加上(或减去)同一个整式,等式仍然成立。等式两边同时乘或除以同一个不为0的整式,等式仍然成立,据此分析即可.
8.A
解:如图,
∵∠1+∠2=180°,∠5+∠2=180°,
∴∠1=∠5,
∴a∥b,
∴∠4=∠6,
∵∠3=108°,
∴∠6=180°﹣108°=72°,
∴∠4=72°.
故答案为:A
先根据题意等量代换得到∠1=∠5,进而根据平行线的判定(同位角)结合平行线的性质(内错角)得到∠4=∠6,再根据邻补角结合题意进行角的运算即可求解。
9.D
解:∵二元一次方程组的解是,
∴,
①+②,得,
故答案为:D .
把代入二元一次方程组,得到,然后两方程相加即可求解.
10.A
11.1
解:由题意得:
,解得:,
当2x-3≥-x+3时,x≥2,
∴当x≥2时,y=min{2x-3,-x+3}=-x+3,
此时该函数的最大值为1;
当2x-3≤-x+3时,x≤2,
∴当x≤2时,y=min{2x-3,-x+3}=2x-3,
此时该函数的最大值为1;
综上所述,y=min{2x-3,-x+3}的最大值是当x=2
所对应的y的值,即y=1,
故答案为:1
根据题意建立方程组,解方程组可得,再分情况讨论:结合新定义列式计算即可求出答案.
12.①②③④
13.
14.或或
15.62°
解:由翻折的性质得:∠DED'=2∠DEF,
∵∠1=56°,
∴∠DED'=180°-∠1=124°,
∴∠DEF=62°,
又∵AD∥BC,
∴∠EFB=∠DEF=62°.
故答案为:62°.
根据折叠性质得出∠DED'=2∠DEF,由邻补角定义求出∠DED',即可求出∠DEF的度数,进而根据二直线平行,内错角相等得到答案.
16.5
17.(1)y=-2x+3;(2)a的值是-2.
18.(1)解:如图所示,即为所求:
(2)平行;相等
(3)解:的面积为:.
解:(2)连接、,
由平移变换的性质可知,线段与的位置关系是平行,数量关系是相等,
故答案为:平行,相等.
(1)由点A及其对应点得出平移方式为:先向左移5格,再向下移2格,据此作出点B和点C的对应点,再顺次连接即可;
(2)根据平移变换的性质:对应点所连的线段相等且互相平行或在一条直线上,即可解题.
(3)在网格图中,利用割补法求出的面积,即可解题.
19.(1)
(2)1
(3)
20.解:原式=()+()-()
=
=()+()+()
=
将代入,原式==-6.
先利用平方差公式,单项式乘多项式和完全平方公式进行计算,然后合并同类项,最后将代入求出答案即可.
21.(1)
(2)不变,比值2:1
(3)
22.(1)解: 设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,
依题意,得: ,
解得: .
故答案为:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
(2)解: ①依题意,得:3m+2n=21,
∴m=7﹣ n.
又∵m,n均为非负整数,
∴ 或 或 或 .
答:共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车.
②方案1所需租车费为120×1+100×9=1020(元),
方案2所需租车费为120×3+100×6=960(元),
方案3所需租车费为120×5+100×3=900(元),
方案4所需租车费为120×7=840(元).
∵1020>960>900>840,
故答案为:最省钱的租车方案是租用7辆A型车,最少租车费是840元.
(1)根据用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨,列方程组求解即可;
(2)先求出m=7﹣ n,再分类讨论求解即可。
23.(1)
(2)
(3)
(4)
24.(1)解:.
平分 .
(2)解:如图, 延长 交 于点 .
,,
,,,
平分 , 平分 ,
,,
,
,
.
(1)利用平行线的性质可得的度数,再通过角平分线的定义求得 的度数.
(2)利用平行线的性质可得、的度数,再通过角平分线的定义得到、的度数,进而求得的度数,然后由三角形的外角性质求得 的度数.
2024-2025学年七年级下册期中考试(浙教版专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共10小题,每题3分, 共30分.)
1.如图,沿路线行走,若,,则( )
A. B. C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,大正方形的边长为m,小正方形的边长为n,x,y表示四个相同长方形的两边长.则①;②;③;④中,正确的是( )
A.①③④ B.②④ C.①③ D.①②③④
4.若方程组的解x、y 的值相等,则a的值为( )
A.2 B.4 C. D.1
5.如图,将沿着点到的方向平移到的位置,,,平移距离为6,则阴影部分面积为( )
A.54 B.42 C.36 D.24
6.在数学活动课上,一位同学用四张完全一样的长方形纸片(长为a,宽为b,)搭成如图一个大正方形,面积为132,中间空缺的小正方形的面积为28.下列结论中,不正确的有( )
A.; B. C. D.
7.已知,,是实数,若,则( )
A. B. C. D.
8.如图, ∠1+∠2=180°, ∠3=108°, 则∠4= ( ).
A.72° B.80° C.82° D.108°
9.若关于x,y的二元一次方程组的解是,则的值为( )
A. B. C.1 D.3
10.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
A.ab B.2ab C.a2﹣ab D.b2+ab
二、填空题(共6小题,每题3分, 共18分.)
11.对于实数a,b,我们定义符号的意义为:当时,;当时,.如:,则关于的函数为的最大值是 .
12.定义:如果一个数的平方等于,记为,那么这个数叫做虚数单位,把形如(a,b为实数)的数叫做复数,其中a叫做这个复数的实部,叫做这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:.
根据以上信息,下列各式:
①;
②;
③
④.
其中正确的是 (填上所有正确答案的序号).
13.已知代数式,则代数式的值是 .
14.射线,,,是同一平面内互不重合的四条射线,,,,则的度数为 .
15.如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D'、C'的位置处,若∠1=56°,则∠EFB的度数是 .
16.如果a,b都是有理数,且满足,则的值为 .
三、解答题(本大题有7个小题,共72分. 解答应写出文字说明、证明过程或演算步骤.)
17.已知关于x、y的方程组
(1)求x与y的关系式(用只含x的代数式表示y).
(2)若x、y的解满足x-y=-3,求a的值.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,三个顶点的位置如图所示,现将平移,使点A移动到点,点,点分别是B、C的对应点.
(1)请画出平移后的;
(2)连接、,则线段与的位置关系是 ,数量关系是 ;
(3)求的面积.
19.计算:
(1);
(2).(利用乘法公式计算)
(3).
20.先化简,再求值:,其中.
21.如图,已知,,点是射线上一动点(与点不重合),,分别平分和,分别交射线于点,.
(1)求的度数;
(2)当点运动时,的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点运动到某处时,,求此时的度数.
22.某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.
(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;
②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
23.通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
例如:如图①是一个长为,宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
(1)观察图②,请你写出之间的等量关系是 ;
(2)根据(1)中的等量关系解决如下问题:
若,,求的值;
类似的,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(3)根据图③,写出一个代数恒等式: ;
(4)已知,,利用上面的规律求的值.
24.如图, 已知直线 . 点 分别在直线 与 上, 平分 平分 交于点 , .
(1) 求 的度数.
(2) 将线段 沿 方向平移, 使点 在点 的左侧, 其他条件不变, 请在备用图中判断 的度数是否改变? 若改变, 求出它的度数 (用含 的式子表示); 若不变,请说明理由.
答案解析部分
1.B
2.C
3.D
解:①由图得,故①正确;
②由图得
,
,
,
故②正确;
③由图得
,
,
,
;
故③正确;
④由得,
,
,
,
,
;
故④正确;
故答案为:D.
根据边长关系判断①;根据判断 ② ;根据平方差公式判断③ ;根据完全平方公式的变形判断④解题.
4.A
5.B
6.D
解:由拼图可得,大正方形的边长为,中间的小正方形的边长为,
∴,,
故选项A正确,不符合题意;
∵,,
∴,
∴,,
故选项B,C正确,不符合题意;
∵,,
∴,
∵,
∴,
故选项D错误,符合题意.
故答案为:D.
根据拼图得出,,,由②可判断A;①-②可求得ab的值,进而可判断B;算式①结合ab的值可求得a2+b2,进而可判断C;①×②再开方可得a2-b2,进而可判断D.
7.C
解:A、无法证明c是否为0,则本项不一定正确;
B、等式左边为加,右边为减,则本项错误;
C、∵则本项正确;
D、无法判断该项的正确性;
故答案为:C.
根据等式的基本性质:等式两边同时加上(或减去)同一个整式,等式仍然成立。等式两边同时乘或除以同一个不为0的整式,等式仍然成立,据此分析即可.
8.A
解:如图,
∵∠1+∠2=180°,∠5+∠2=180°,
∴∠1=∠5,
∴a∥b,
∴∠4=∠6,
∵∠3=108°,
∴∠6=180°﹣108°=72°,
∴∠4=72°.
故答案为:A
先根据题意等量代换得到∠1=∠5,进而根据平行线的判定(同位角)结合平行线的性质(内错角)得到∠4=∠6,再根据邻补角结合题意进行角的运算即可求解。
9.D
解:∵二元一次方程组的解是,
∴,
①+②,得,
故答案为:D .
把代入二元一次方程组,得到,然后两方程相加即可求解.
10.A
11.1
解:由题意得:
,解得:,
当2x-3≥-x+3时,x≥2,
∴当x≥2时,y=min{2x-3,-x+3}=-x+3,
此时该函数的最大值为1;
当2x-3≤-x+3时,x≤2,
∴当x≤2时,y=min{2x-3,-x+3}=2x-3,
此时该函数的最大值为1;
综上所述,y=min{2x-3,-x+3}的最大值是当x=2
所对应的y的值,即y=1,
故答案为:1
根据题意建立方程组,解方程组可得,再分情况讨论:结合新定义列式计算即可求出答案.
12.①②③④
13.
14.或或
15.62°
解:由翻折的性质得:∠DED'=2∠DEF,
∵∠1=56°,
∴∠DED'=180°-∠1=124°,
∴∠DEF=62°,
又∵AD∥BC,
∴∠EFB=∠DEF=62°.
故答案为:62°.
根据折叠性质得出∠DED'=2∠DEF,由邻补角定义求出∠DED',即可求出∠DEF的度数,进而根据二直线平行,内错角相等得到答案.
16.5
17.(1)y=-2x+3;(2)a的值是-2.
18.(1)解:如图所示,即为所求:
(2)平行;相等
(3)解:的面积为:.
解:(2)连接、,
由平移变换的性质可知,线段与的位置关系是平行,数量关系是相等,
故答案为:平行,相等.
(1)由点A及其对应点得出平移方式为:先向左移5格,再向下移2格,据此作出点B和点C的对应点,再顺次连接即可;
(2)根据平移变换的性质:对应点所连的线段相等且互相平行或在一条直线上,即可解题.
(3)在网格图中,利用割补法求出的面积,即可解题.
19.(1)
(2)1
(3)
20.解:原式=()+()-()
=
=()+()+()
=
将代入,原式==-6.
先利用平方差公式,单项式乘多项式和完全平方公式进行计算,然后合并同类项,最后将代入求出答案即可.
21.(1)
(2)不变,比值2:1
(3)
22.(1)解: 设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,
依题意,得: ,
解得: .
故答案为:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
(2)解: ①依题意,得:3m+2n=21,
∴m=7﹣ n.
又∵m,n均为非负整数,
∴ 或 或 或 .
答:共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车.
②方案1所需租车费为120×1+100×9=1020(元),
方案2所需租车费为120×3+100×6=960(元),
方案3所需租车费为120×5+100×3=900(元),
方案4所需租车费为120×7=840(元).
∵1020>960>900>840,
故答案为:最省钱的租车方案是租用7辆A型车,最少租车费是840元.
(1)根据用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨,列方程组求解即可;
(2)先求出m=7﹣ n,再分类讨论求解即可。
23.(1)
(2)
(3)
(4)
24.(1)解:.
平分 .
(2)解:如图, 延长 交 于点 .
,,
,,,
平分 , 平分 ,
,,
,
,
.
(1)利用平行线的性质可得的度数,再通过角平分线的定义求得 的度数.
(2)利用平行线的性质可得、的度数,再通过角平分线的定义得到、的度数,进而求得的度数,然后由三角形的外角性质求得 的度数.
同课章节目录
