2024-2025学年七年级下学期数学期中考试(浙江专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中考试(浙江专用)[答案+解析] |

|
|
| 格式 | docx | ||
| 文件大小 | 413.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览



文档简介
保密★启用前
2024-2025学年七年级下册期中考试(浙江专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每题3分,共30分)
1.清代诗人袁枚的一首诗《苔》中写到:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为米,则数据用科学记数法表示为( )
A. B. C. D.
2.下列图形中,可以由其中一个图形通过平移得到的是( )
A. B. C. D.
3.在下列计算中,正确的是( )
A.a3 a3=3a6 B.(-3a2)3=-27a6
C.a3+a4=a7 D.a6÷a2=a3
4.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中、都与地面平行,与平行,若,则的度数为( )
A. B. C. D.
5.如图,下列说理中,正确的是( )
A.因为,所以 B.因为,所以
C.因为,所以 D.因为,所以
6.如图,直线a∥b,将三角尺的直角顶点放在直线上,如果∠2=60°,那么∠1的度数为( )
A.30° B.40° C.50° D.60°
7.下列计算正确的是( )
A. B. C. D.
8.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空”.诗中后两句的意思是如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房,据此求客房和客人的数量,对于甲、乙、丙三人的解题方案,判断正确的个数是( )
甲:设客房有x间,则;
乙:设客人有y人,则;
丙:设客房有x间,客人有y人,则.
A.0个 B.1个 C.2个 D.3个
9.若是二元一次方程组的解,则的算术平方根为( )
A.9 B. C. D.3
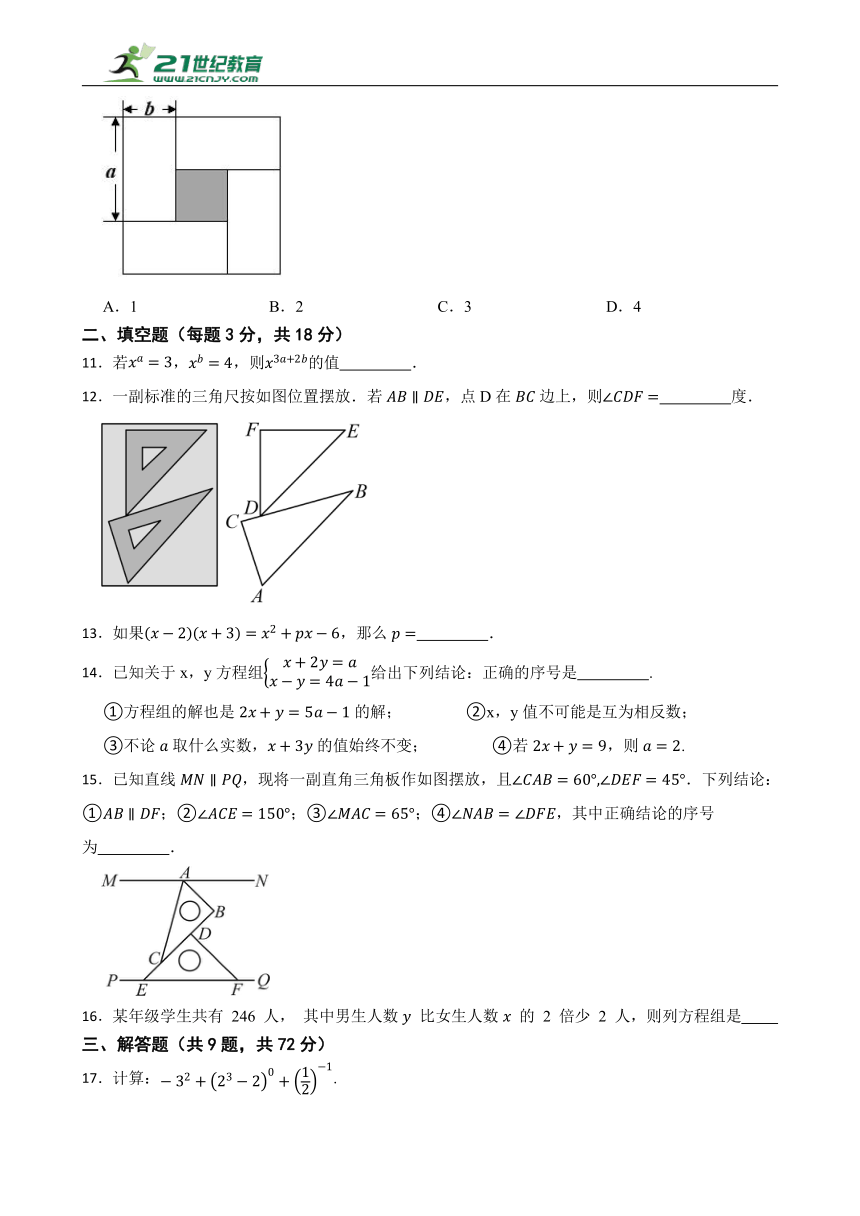
10.如图,由4个全等的小长方形与一个小正方形密铺成一个大的正方形图案,该图案的面积为100,里面的小正方形的面积为16,若小长方形的长为a,宽为b,则下列关系式中:①;②;③;④,正确的有( )个
A.1 B.2 C.3 D.4
二、填空题(每题3分,共18分)
11.若,,则的值 .
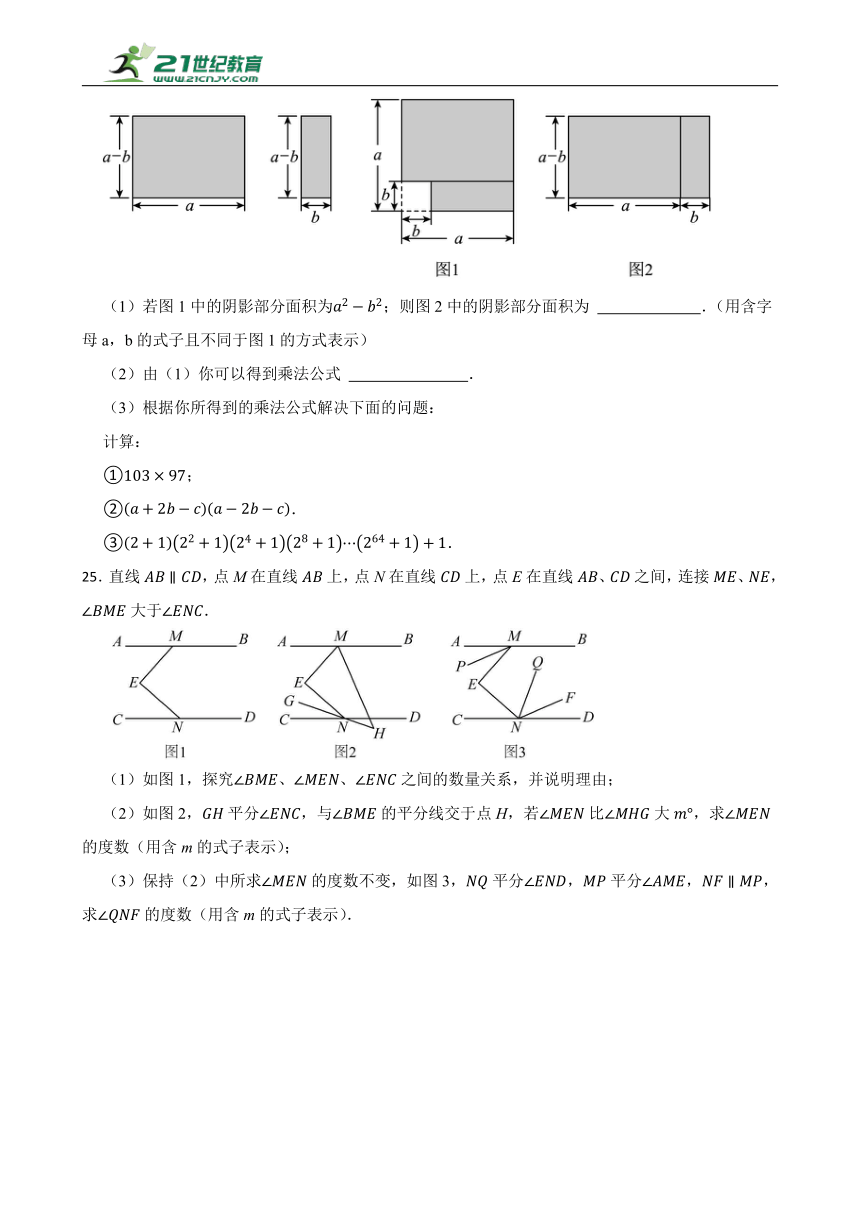
12.一副标准的三角尺按如图位置摆放.若,点D在边上,则 度.
13.如果,那么 .
14.已知关于x,y方程组给出下列结论:正确的序号是 .
①方程组的解也是的解; ②x,y值不可能是互为相反数;
③不论取什么实数,的值始终不变; ④若,则.
15.已知直线,现将一副直角三角板作如图摆放,且.下列结论:①;②;③;④,其中正确结论的序号为 .
16.某年级学生共有 246 人, 其中男生人数 比女生人数 的 2 倍少 2 人,则列方程组是
三、解答题(共9题,共72分)
17.计算:.
18. 计算:
19.先化简,再求值,其中,.
20.先化简,再求值:,其中.
21.解下列方程组:
(1);
(2).
22. 补全证明过程:(括号内填写理由)
如图,,求证:
证明:∵(已知),
∴( ▲ ),
∴ ▲ ( ▲ ),又∵(已知),
▲ ,
∴ ▲ ▲ ( ▲ ),
∴( ▲ ).
23.某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.
(1)求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.
(2)该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.
(3)若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.
24.如图所示,两个长方形用不同形式拼成图1和图2两个图形.
(1)若图1中的阴影部分面积为;则图2中的阴影部分面积为 .(用含字母a,b的式子且不同于图1的方式表示)
(2)由(1)你可以得到乘法公式 .
(3)根据你所得到的乘法公式解决下面的问题:
计算:
①;
②.
③.
25.直线,点M在直线上,点N在直线上,点E在直线、之间,连接、,大于.
(1)如图1,探究、、之间的数量关系,并说明理由;
(2)如图2,平分,与的平分线交于点H,若比大,求的度数(用含m的式子表示);
(3)保持(2)中所求的度数不变,如图3,平分,平分,,求的度数(用含m的式子表示).
答案解析部分
1.B
2.C
3.B
解:A. a3 a3=a6≠3a6,计算错误,不符合题意;
B:(-3a2)3=-27a6,计算正确,符合题意;
C:a3+a4≠a7,计算错误,不符合题意;
D:a6÷a2=a4≠a3,计算错误,不符合题意;
故答案为:B.
根据同底数幂的乘除法则,幂的乘方,积的乘方法则,合并同类项等计算求解即可。
4.D
解:∵,
∴,
∵,
∴,
∴,
故答案为:D.
根据平行得到,,解题即可.
5.C
6.A
解:如图所示,
故答案为:A.
利用两直线平行同位角相等,可把转移到的位置上,再利用平角的概念即可.
7.C
解:,故A错误;
,故B错误;
,故C正确;
,不是同类项,无法合并,故D错误.
故答案为:C.
(1)利用同底数幂的除法计算;
(2)利用完全平方公式计算;
(3)利用幂的乘方法则计算;
(4)利用合并同类项法则计算.
8.C
9.D
解:把 代入方程组中,
得
①-②得:x+2y=9,
∴的算术平方根为3;
故答案为:D.
把 代入原方程组中可得关于x、y的新方程组,将两方程相加可得x+2y值,再求其算术平方根即可.
10.C
11.432
12.105
13.
14.①③④
解:①将方程组中两个方程相加,得
∴方程组的解也是 的解,故①正确;
②解方程组 得,
当x,y的值互为相反数时,
即
解得
∴当 时,x,y的值互为相反数,故②不正确;
③原方程组的解为,
∴不论a取什么实数, 的值始终不变,都为 故③正确;
④若 则
解得 故④正确;
综上, ①③④正确.
故答案为:①③④.
两方程相加计算判断①;求出方程组的解x,y的值,根据互为相反数求出a的值判断②;求出的值判断③;根据求出a的值判断④解答即可.
15.①②④
16.
解:设男生的人数为y,女生的人数为x,
根据题意可得:,
故答案为:.
设男生的人数为y,女生的人数为x,根据“ 某年级学生共有 246 人, 其中男生人数 比女生人数 的 2 倍少 2 人 ”直接列出方程组即可.
17.
18.解:原式
.
根据零指数幂和负整数指数幂的法则,求算术平方根的法则和化简绝对值的法则,从左到右依次计算即可。
19.解:
,
当,时,原式
先利用完全平方公式和多项式除以单项式的法则,先去括号,再合并同类项,然后将x、y值代入化简式计算即可.
20.解:
当时
原式
先运用平方差公式、完全平方公式进行运算化简,再代入数值即可求解。
21.(1)
(2)
22.证明:∵(已知)
(同旁内角互补两直线平行),
(两直线平行,内错角相等),
又(已知)
∴,
(内错角相等,两直线平行),
(两直线平行,内错角相等).
利用同旁内角互补两直线平行,可证得AB∥CD,利用平行线的性质可证得∠BAP=∠APC,结合已知条件可证得∠EAP=∠FPA,利用平行线的判定可证得AE∥FP,然后利用平行线的性质,可证得结论.
23.(1)解:设“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元,
由题意得,,解方程组得,,
∴“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元.
(2)解:设购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,
由题意得,,
整理得,,
∵、为正整数,
∴或或,
∴专卖店共有种采购方案.
(3)解:当,时,利润为:(元);
当,时,利润为:(元);
当,时,利润为:(元);
∵,
∴利润最大的采购方案为购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,最大利润为元.
(1)设“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元,根据题意列出方程组,再求解即可;
(2)设购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,根据题意列出方程,再求解即可;
(3)将(2)中的各种方案的费用求出,再比较大小即可。
24.(1)
(2)
(3)①;②;③
25.(1)解:;
理由如下:
过作,
,
,
,
,
,
,
;
(2)解:如图,过作,
,
,
平分,
,
,
,
,
,
平分,
,
,
,
,
,
比大,
,
,
,
;
(3)解:如图,过作,
,
,
,
,
,
平分,
平分,
,
,
,
,
,
,
,
,
,
.
(1)∠MEN+∠BME-∠ENC=180°,理由如下:过点E作EF∥AB,由二直线平行,同旁内角互补得∠MEF=180°-∠BME,由平行于同一直线的两条直线互相平行得EF∥CD,由二直线平行,内错角相等,得∠FEN=∠ENC,进而根据角的构成可得∠MEN=∠MEF+∠FEN,再等量替换即可得出得出结论;
(2)过点H作PQ∥AB,由平行线的性质得∠PHN+∠MHG=∠BMH,∠PHN=∠CNG,结合角平分线的定义得∠MHG=(∠BME-∠ENC)=90°-∠MEN,从而即可求解;
(3)过点E作ER∥NF,由平行线的性质得∠NER+∠ENQ+∠FNQ=180°,则∠MEN-∠MER+∠ENQ+∠FNQ=180°,结合角平分线的定义得∠MER=90°-∠BME,从而代入即可求解.
2024-2025学年七年级下册期中考试(浙江专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每题3分,共30分)
1.清代诗人袁枚的一首诗《苔》中写到:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为米,则数据用科学记数法表示为( )
A. B. C. D.
2.下列图形中,可以由其中一个图形通过平移得到的是( )
A. B. C. D.
3.在下列计算中,正确的是( )
A.a3 a3=3a6 B.(-3a2)3=-27a6
C.a3+a4=a7 D.a6÷a2=a3
4.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中、都与地面平行,与平行,若,则的度数为( )
A. B. C. D.
5.如图,下列说理中,正确的是( )
A.因为,所以 B.因为,所以
C.因为,所以 D.因为,所以
6.如图,直线a∥b,将三角尺的直角顶点放在直线上,如果∠2=60°,那么∠1的度数为( )
A.30° B.40° C.50° D.60°
7.下列计算正确的是( )
A. B. C. D.
8.我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空”.诗中后两句的意思是如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房,据此求客房和客人的数量,对于甲、乙、丙三人的解题方案,判断正确的个数是( )
甲:设客房有x间,则;
乙:设客人有y人,则;
丙:设客房有x间,客人有y人,则.
A.0个 B.1个 C.2个 D.3个
9.若是二元一次方程组的解,则的算术平方根为( )
A.9 B. C. D.3
10.如图,由4个全等的小长方形与一个小正方形密铺成一个大的正方形图案,该图案的面积为100,里面的小正方形的面积为16,若小长方形的长为a,宽为b,则下列关系式中:①;②;③;④,正确的有( )个
A.1 B.2 C.3 D.4
二、填空题(每题3分,共18分)
11.若,,则的值 .
12.一副标准的三角尺按如图位置摆放.若,点D在边上,则 度.
13.如果,那么 .
14.已知关于x,y方程组给出下列结论:正确的序号是 .
①方程组的解也是的解; ②x,y值不可能是互为相反数;
③不论取什么实数,的值始终不变; ④若,则.
15.已知直线,现将一副直角三角板作如图摆放,且.下列结论:①;②;③;④,其中正确结论的序号为 .
16.某年级学生共有 246 人, 其中男生人数 比女生人数 的 2 倍少 2 人,则列方程组是
三、解答题(共9题,共72分)
17.计算:.
18. 计算:
19.先化简,再求值,其中,.
20.先化简,再求值:,其中.
21.解下列方程组:
(1);
(2).
22. 补全证明过程:(括号内填写理由)
如图,,求证:
证明:∵(已知),
∴( ▲ ),
∴ ▲ ( ▲ ),又∵(已知),
▲ ,
∴ ▲ ▲ ( ▲ ),
∴( ▲ ).
23.某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.
(1)求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.
(2)该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.
(3)若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.
24.如图所示,两个长方形用不同形式拼成图1和图2两个图形.
(1)若图1中的阴影部分面积为;则图2中的阴影部分面积为 .(用含字母a,b的式子且不同于图1的方式表示)
(2)由(1)你可以得到乘法公式 .
(3)根据你所得到的乘法公式解决下面的问题:
计算:
①;
②.
③.
25.直线,点M在直线上,点N在直线上,点E在直线、之间,连接、,大于.
(1)如图1,探究、、之间的数量关系,并说明理由;
(2)如图2,平分,与的平分线交于点H,若比大,求的度数(用含m的式子表示);
(3)保持(2)中所求的度数不变,如图3,平分,平分,,求的度数(用含m的式子表示).
答案解析部分
1.B
2.C
3.B
解:A. a3 a3=a6≠3a6,计算错误,不符合题意;
B:(-3a2)3=-27a6,计算正确,符合题意;
C:a3+a4≠a7,计算错误,不符合题意;
D:a6÷a2=a4≠a3,计算错误,不符合题意;
故答案为:B.
根据同底数幂的乘除法则,幂的乘方,积的乘方法则,合并同类项等计算求解即可。
4.D
解:∵,
∴,
∵,
∴,
∴,
故答案为:D.
根据平行得到,,解题即可.
5.C
6.A
解:如图所示,
故答案为:A.
利用两直线平行同位角相等,可把转移到的位置上,再利用平角的概念即可.
7.C
解:,故A错误;
,故B错误;
,故C正确;
,不是同类项,无法合并,故D错误.
故答案为:C.
(1)利用同底数幂的除法计算;
(2)利用完全平方公式计算;
(3)利用幂的乘方法则计算;
(4)利用合并同类项法则计算.
8.C
9.D
解:把 代入方程组中,
得
①-②得:x+2y=9,
∴的算术平方根为3;
故答案为:D.
把 代入原方程组中可得关于x、y的新方程组,将两方程相加可得x+2y值,再求其算术平方根即可.
10.C
11.432
12.105
13.
14.①③④
解:①将方程组中两个方程相加,得
∴方程组的解也是 的解,故①正确;
②解方程组 得,
当x,y的值互为相反数时,
即
解得
∴当 时,x,y的值互为相反数,故②不正确;
③原方程组的解为,
∴不论a取什么实数, 的值始终不变,都为 故③正确;
④若 则
解得 故④正确;
综上, ①③④正确.
故答案为:①③④.
两方程相加计算判断①;求出方程组的解x,y的值,根据互为相反数求出a的值判断②;求出的值判断③;根据求出a的值判断④解答即可.
15.①②④
16.
解:设男生的人数为y,女生的人数为x,
根据题意可得:,
故答案为:.
设男生的人数为y,女生的人数为x,根据“ 某年级学生共有 246 人, 其中男生人数 比女生人数 的 2 倍少 2 人 ”直接列出方程组即可.
17.
18.解:原式
.
根据零指数幂和负整数指数幂的法则,求算术平方根的法则和化简绝对值的法则,从左到右依次计算即可。
19.解:
,
当,时,原式
先利用完全平方公式和多项式除以单项式的法则,先去括号,再合并同类项,然后将x、y值代入化简式计算即可.
20.解:
当时
原式
先运用平方差公式、完全平方公式进行运算化简,再代入数值即可求解。
21.(1)
(2)
22.证明:∵(已知)
(同旁内角互补两直线平行),
(两直线平行,内错角相等),
又(已知)
∴,
(内错角相等,两直线平行),
(两直线平行,内错角相等).
利用同旁内角互补两直线平行,可证得AB∥CD,利用平行线的性质可证得∠BAP=∠APC,结合已知条件可证得∠EAP=∠FPA,利用平行线的判定可证得AE∥FP,然后利用平行线的性质,可证得结论.
23.(1)解:设“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元,
由题意得,,解方程组得,,
∴“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元.
(2)解:设购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,
由题意得,,
整理得,,
∵、为正整数,
∴或或,
∴专卖店共有种采购方案.
(3)解:当,时,利润为:(元);
当,时,利润为:(元);
当,时,利润为:(元);
∵,
∴利润最大的采购方案为购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,最大利润为元.
(1)设“冰墩墩”毛绒玩具每只进价为元,“雪容融”毛绒玩具每只进价为元,根据题意列出方程组,再求解即可;
(2)设购进“冰墩墩”毛绒玩具只,购进“雪容融”毛绒玩具只,根据题意列出方程,再求解即可;
(3)将(2)中的各种方案的费用求出,再比较大小即可。
24.(1)
(2)
(3)①;②;③
25.(1)解:;
理由如下:
过作,
,
,
,
,
,
,
;
(2)解:如图,过作,
,
,
平分,
,
,
,
,
,
平分,
,
,
,
,
,
比大,
,
,
,
;
(3)解:如图,过作,
,
,
,
,
,
平分,
平分,
,
,
,
,
,
,
,
,
,
.
(1)∠MEN+∠BME-∠ENC=180°,理由如下:过点E作EF∥AB,由二直线平行,同旁内角互补得∠MEF=180°-∠BME,由平行于同一直线的两条直线互相平行得EF∥CD,由二直线平行,内错角相等,得∠FEN=∠ENC,进而根据角的构成可得∠MEN=∠MEF+∠FEN,再等量替换即可得出得出结论;
(2)过点H作PQ∥AB,由平行线的性质得∠PHN+∠MHG=∠BMH,∠PHN=∠CNG,结合角平分线的定义得∠MHG=(∠BME-∠ENC)=90°-∠MEN,从而即可求解;
(3)过点E作ER∥NF,由平行线的性质得∠NER+∠ENQ+∠FNQ=180°,则∠MEN-∠MER+∠ENQ+∠FNQ=180°,结合角平分线的定义得∠MER=90°-∠BME,从而代入即可求解.
同课章节目录
