2025中考物理三轮高频易错点专练--07质量与密度(答案+解析)
文档属性
| 名称 | 2025中考物理三轮高频易错点专练--07质量与密度(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-13 00:03:31 | ||
图片预览



文档简介
07质量与密度
一、质量
1.义务教育物理课程体现了“从生活走向物理,从物理走向社会”的理念,贴近大家的生活。下列对生活中物理量的估计,与实际最接近的是( )
A.乒乓球被誉为我国的“国球”,其直径约为40mm
B.人的脉搏跳动一次的时间约为10s
C.一瓶矿泉水的质量约为55g
D.正常人的体温约为38.5℃
2.一个初中学生的质量最接近于( )
A.50千克 B.500千克 C.50牛 D.500牛
3.物理在生活中无处不在,下列关于在教室里的物理现象分析错误的是( )
A.利用电子白板讲题时,老师应关掉白板上方的灯,避免干扰学生看白板上的内容
B.老师在教室里讲话时听不到回声是因为教室里没有回声
C.冬天教室窗玻璃起雾,雾在教室内侧的玻璃上
D.老师用粉笔在黑板上书写后,粉笔的质量变小
4.遨游九天,筑梦苍穹,中国人对太空的探索永不止步。2024年10月30日,神舟十九号 载人飞船成功发射并与天和核心舱形成组合体(如图所示),乘组顺利进驻中国空间站。神舟十九号飞船发射时,以神舟十九号中的航天员为参照物,神舟十九号飞船是 的,航天员从地面来到空间站内,其质量 (填变化情况);航天器的外壳要求轻巧、耐高温,那么用来制造航天器外壳的材料应具有的特性是:密度 且熔点高。
二、质量的测量
5.用天平测完物体质量后,发现左盘上黏有一小块橡皮泥。下列分析正确的是( )
A.若橡皮泥是在调横梁水平前黏上去的,则测量结果仍然准确
B.若橡皮泥是在调横梁水平后黏上去的,则测出的质量小于物体的真实质量
C.橡皮泥无论是在什么时候黏上去的,测量结果都不准确
D.如果橡皮泥质量较小,对天平的测量不会起什么作用
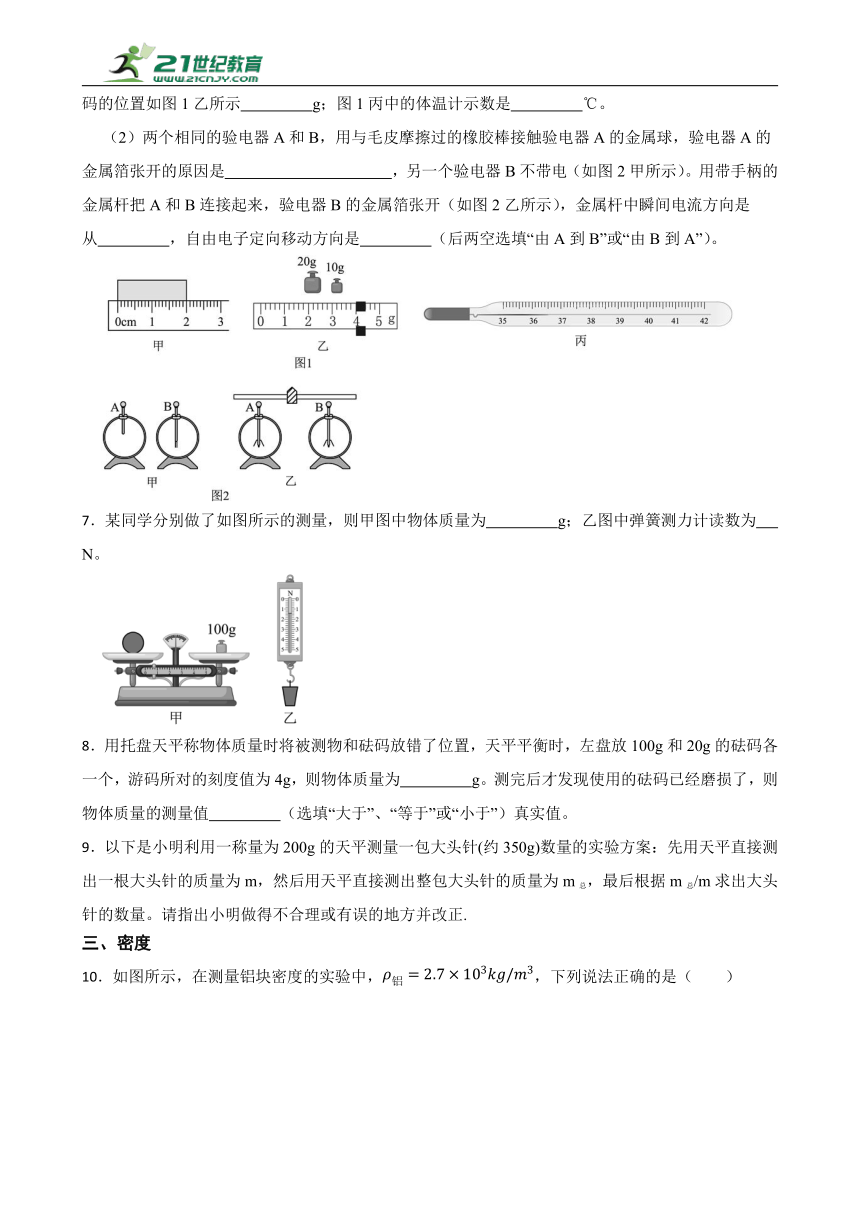
6.(1)如图1甲所示,图甲中木块的长度为 cm,天平平衡时,放在天平右盘中的砝码和游码的位置如图1乙所示 g;图1丙中的体温计示数是 ℃。
(2)两个相同的验电器A和B,用与毛皮摩擦过的橡胶棒接触验电器A的金属球,验电器A的金属箔张开的原因是 ,另一个验电器B不带电(如图2甲所示)。用带手柄的金属杆把A和B连接起来,验电器B的金属箔张开(如图2乙所示),金属杆中瞬间电流方向是从 ,自由电子定向移动方向是 (后两空选填“由A到B”或“由B到A”)。
7.某同学分别做了如图所示的测量,则甲图中物体质量为 g;乙图中弹簧测力计读数为 N。
8.用托盘天平称物体质量时将被测物和砝码放错了位置,天平平衡时,左盘放100g和20g的砝码各一个,游码所对的刻度值为4g,则物体质量为 g。测完后才发现使用的砝码已经磨损了,则物体质量的测量值 (选填“大于”、“等于”或“小于”)真实值。
9.以下是小明利用一称量为200g的天平测量一包大头针(约350g)数量的实验方案:先用天平直接测出一根大头针的质量为m,然后用天平直接测出整包大头针的质量为m总,最后根据m总/m求出大头针的数量。请指出小明做得不合理或有误的地方并改正.
三、密度
10.如图所示,在测量铝块密度的实验中,,下列说法正确的是( )
A.测量过程中可以移动平衡螺母将天平调平
B.铝块是空心的
C.所测铝块的质量为52.4g
D.如果把铝块打磨掉一部分铝屑,则剩余铝块密度将不变
11.下列物理量的符号和国际单位,对应错误的是( )
A.速度v-m/s B.质量m-kg
C.密度ρ-kg/m3 D.功率P-J
12.杯中的某种溶液,倒掉一半后,对剩下的半杯溶液描述不正确的是
A.热值不变 B.密度不变 C.质量减半 D.比热容减半
13.两个实心物体a、b的体积与质量的关系如图所示.下列说法正确的是( )
A.a的密度是b的密度的2倍
B.b的密度是a的密度的2倍
C.a的密度是0.5×103kg/m3
D.a、b的密度与它们的质量、体积有关
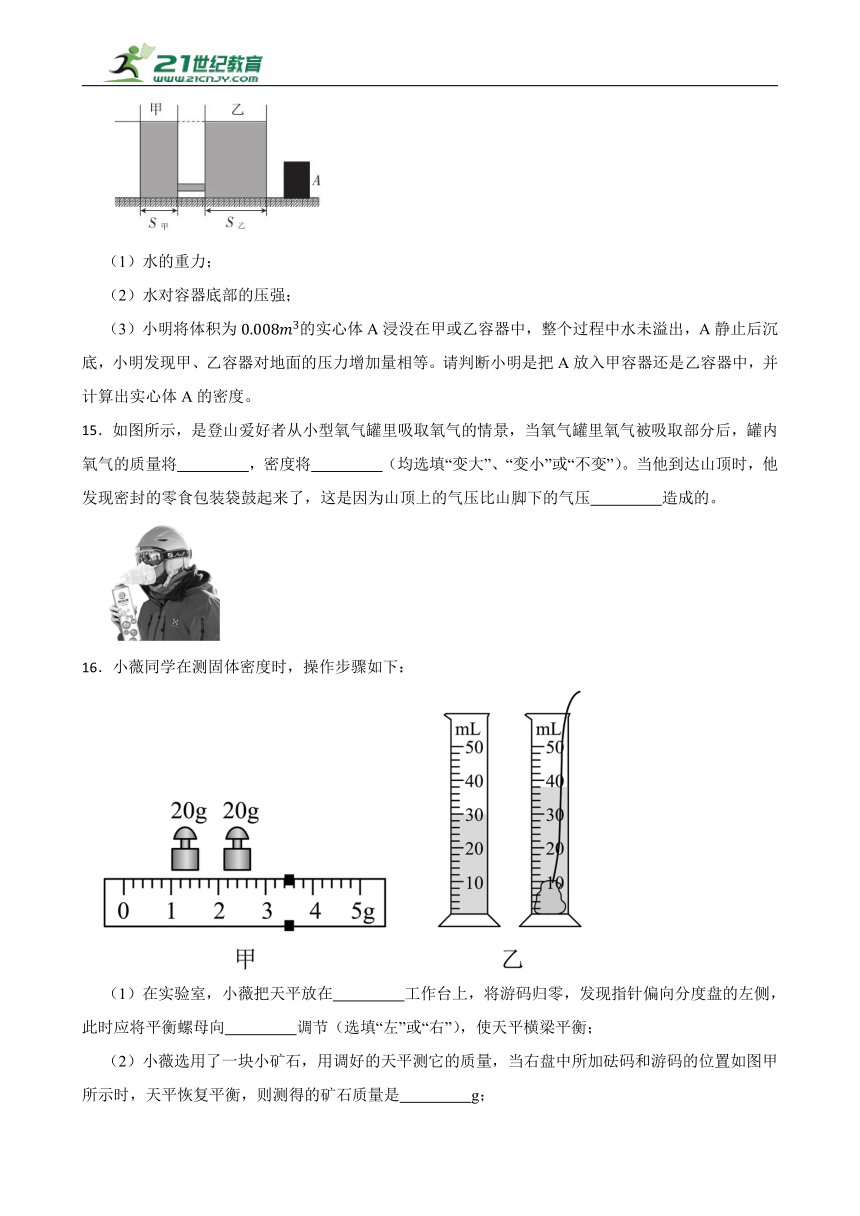
14.如图所示,盛有60kg水的柱形容器甲、乙置于水平地面上,容器足够高,两容器底部用软细管(体积忽略不计)连通。已知甲、乙容器底面积分别为、,,。求:
(1)水的重力;
(2)水对容器底部的压强;
(3)小明将体积为的实心体A浸没在甲或乙容器中,整个过程中水未溢出,A静止后沉底,小明发现甲、乙容器对地面的压力增加量相等。请判断小明是把A放入甲容器还是乙容器中,并计算出实心体A的密度。
15.如图所示,是登山爱好者从小型氧气罐里吸取氧气的情景,当氧气罐里氧气被吸取部分后,罐内氧气的质量将 ,密度将 (均选填“变大”、“变小”或“不变”)。当他到达山顶时,他发现密封的零食包装袋鼓起来了,这是因为山顶上的气压比山脚下的气压 造成的。
16.小薇同学在测固体密度时,操作步骤如下:
(1)在实验室,小薇把天平放在 工作台上,将游码归零,发现指针偏向分度盘的左侧,此时应将平衡螺母向 调节(选填“左”或“右”),使天平横梁平衡;
(2)小薇选用了一块小矿石,用调好的天平测它的质量,当右盘中所加砝码和游码的位置如图甲所示时,天平恢复平衡,则测得的矿石质量是 g;
(3)如图乙所示的量筒分度值为 cm3,在量筒中装入适量的水,将系了细线的矿石轻放入量筒,如图乙所示,测得矿石的体积是 cm3;
(4)实验后,小薇发现使用的20g砝码生锈了,由此导致测得的矿石密度会 (选填“偏大”“偏小”或“不变”)。
17.课外兴趣小组需要密度为的盐水,为检验配制的盐水是否合格。
(1)小蓬设计了如下方案:
①用天平测出空烧杯的质量;
②往烧杯中倒入适量盐水,测出烧杯和盐水的总质量;
③将烧杯中的盐水倒入量筒中,测出盐水的体积V;
④则盐水的密度 ;
(2)经分析该方案会使密度测量结果 (选填“偏大”或“偏小”);
(3)小组成员改进了实验方案并进行了如下操作:
将天平放在 桌面上,将游码移至标尺左端的 上,发现指针的位置如图甲所示,则需将平衡螺母向 调节。往烧杯中倒入适量盐水,将烧杯放在天平的 盘,测出烧杯和盐水的总质量为 g;将烧杯中的部分盐水倒入量筒中,如图丙读出盐水的体积为 ;测出烧杯和剩余盐水的质量为15g;计算出盐水的密度为 ;
(4)为配制合格的盐水,需要继续向盐水中 (选填“加盐”或“加水”);
(5)小蓬接着测量了不同体积的牛奶的质量,描绘出质量与体积关系的图线如丙图中A所示。她分析后发现,由于误将烧杯和水的总质量当作了水的质量,导致图线A未经过坐标原点,由此推断:水的质量与体积关系的图线应是 (选填丙图中“B”、“C”或“D”)。
18.质量是物质一种属性,它不随位置、形状、状态和 的改变而改变。近几个月份的汽油价格进行了调整。和大多数物质一样,汽油也有热胀冷缩的性质,随着气温的下降,汽油密度会 (选填“变大”或“变小”),受此因素影响,在每吨汽油价格不变的情况下,每升(每立方分米)汽油的价格会 (选填“上调”或“下调”)。
四、能力提升
19.弹簧测力计下挂一长方体物体,将物体从盛有适量水的烧杯(可看成柱形)上方离水面某一高度处缓缓下降,然后将其逐渐浸入水中,如图甲;图乙是弹簧测力计示数与物体下降高度变化关系的图像,则下列说法错误的是( )
A.物体的体积是
B.物体的密度是
C.物体刚浸没时下表面受到水的压力是4N
D.物体完全浸没后与最初时相比,烧杯底部受到水的压力增大了5N
20.如图甲,用弹簧测力计悬挂的圆柱体缓慢浸入盛水的烧杯中,直至圆柱体浸没在水中,整个过程中弹簧测力计示数F与圆柱体下降高度h变化关系的图像如图乙所示,忽略液面的高度变化,以下判断正确的是( )
A.圆柱体受到重力为8N
B.圆柱体的高度为8cm
C.圆柱体上表面刚进入水时受到浮力为2N
D.圆柱体的密度为1.25×103kg/m3
21.如图所示,质量分布均匀、底面积为200cm2的长方体甲和质量未知的薄壁柱形容器乙放置于水平地面上,已知容器乙的高度为h,其内装有一定量的水。现将甲沿水平方向切去一定的厚度△h,并将甲切下的部分保持竖直轻放入乙容器中,甲、乙对地面的压强随切去厚度△h的变化情况如图丙所示,则下列说法正确的是
A.甲的密度为 200kg/m3
B.乙容器的质量为 2.4kg
C.图丙中 a的值为21cm
D. h=20cm时, 乙容器对桌面的压强为 3100Pa
22.某同学用托盘天平和量筒测量一小石块的密度,如图甲是调节天平时的情形,图乙和图丙分别是测量石块质量和体积时的情形,下列说法正确的是( )
A.甲图中应将平衡螺母向右调,使横梁平衡
B.乙图中测石块质量时,天平的读数是71.2g
C.由丙图量筒的示数测得石块的体积是
D.计算出石块的密度是
23.如图所示,边长分别为0.4m和0.2m的实心正方体A、B放置在水平地面上,A的密度为0.6×103kg/m3,B的密度为0.4×103kg/m3,物体B的重力为 N。为使A、B对水平地面的压强相等,可以将物体A沿竖直方向切下体积V1叠放到物体B上,也可以将物体A沿水平方向切下体积V2叠放到物体B上,则V1与V2之比为 。
24.冰山露出海面的部分只是冰山的一小部分,所以常有“冰山一角”的说法。若海水的密度是 1.1×103kg/m3,冰的密度是 0.9×103kg/m3,则冰山露出海面的体积与海面下的体积之比是 。
25.水平放置的电子秤上有一质量300g、底面积400cm2的长方体薄壁柱形容器,容器内装有一定量的某液体。将质量为900g的实心正方体轻放入液体中,稳定后如图甲所示。打开容器底部的阀门向外排放液体,排放过程中,容器底部所受液体压强与排出液体体积的关系如图乙所示,正方体的密度为 ,当电子秤示数变化2000g时,液体对容器底的压强与容器对电子秤的压强之比为 。
26.小明同学利用力学传感器设计了如图甲所示的装置,竖直细杆B的下端通过力传感器(小方块)固定在容器底部,上端与实心正方体A固定。细杆B长10cm,A不吸水。不计细杆B及连接处的质量和体积。力传感器可以显示出细杆B受到作用力的大小,现缓慢向容器中加水,当水深为20cm时正方体A刚好完全浸没。力传感器的示数大小F随水深h变化的图像如图乙所示。
(,g取)求:
(1)正方体A的重力;
(2)正方体A刚好完全浸没时,水对容器底的压强;
(3)正方体A的密度;
(4)当容器内水的深度为13cm时,正方体A所受浮力的大小及力传感器的示数大小。
五、直击中考
27.如图所示,有一个梯形物体浸没在某种液体中(物体与容器底不紧密接触),容器液面上方近似为真空,液体的密度为ρ,深度为H,物体高度为h,体积为V,较大的下底面面积为S',较小的上底面面积为S",容器的底面面积为S,则该物体受到水向下的压力F等于( )
A.ρg(HS'-V) B.ρgV-ρghS' C.ρghS'-ρgV D.ρg(H-h)S"
28.如图甲中,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中。图乙是钢绳拉力随时间变化的图象。g取10N/kg,水的密度为,若不计水的阻力,下列说法错误的是( )
A.石料的质量为250kg
B.石料的密度为
C.石料所受浮力随石料浸入水中体积的增大而增大
D.石料浸没水中后受到的浮力为1500N且保持不变
29.如图1所示,甲、乙两质地均匀的正方体放在水平地面上,图2为它们对地面的压强与其边长的关系图,g取,下列说法正确的是( )
A.甲物体的密度为
B.甲、乙物体的密度之比为8∶3
C.若边长之比,则对地压强之比
D.若边长之比,则所受重力之比
30.如图所示,长方体物块A重为8N、底面积为40cm2,高为10cm,质量不计的细杆上端固定在天花板上、下端与物块A的上表面相连,足够高的柱形容器重为2N。现向容器中缓慢注水1.8kg,此时水面高20cm,A浸入水中的体积为其总体积的一半,容器的底面积为 ;若将A的左、右两侧沿竖直方向各切掉总体积的四分之一,并将切掉部分放入柱形容器中,此时水对容器底部的压强改变量为,容器对桌面的压强改变量为,则 。
31.雪在外力挤压下可形成冰,表明雪的密度 冰的密度,(选填“大于”、“等于”或“小于”)。小华利用冰的密度(ρ冰),使用如下方法来估测积雪的密度:利用平整地面上的积雪,脚向下用力踩在雪上,将雪踏实成冰并形成一个下凹的脚印,然后测量脚印的深度h和积雪原来的厚度H,就可以估测出积雪的密度,并写出雪的密度的表达式: (用已知物理量符号表示)。若实验时雪没有踩踏实,则所测雪的密度将 (选填“偏大”、“偏小”或“不变”)。
32.如图所示,体积为的正方体物体A水平放置,其密度大于水的密度。另有一足够高的薄壁柱形容器B置于水平地面,底面积为,质量为3kg。(,)
(1)求容器的重力;
(2)向容器B注入体积为的水时,求容器对水平地面的压强;
(3)在(2)问的前提下,再将物体A放入容器中,此时容器对地面的压强与水对容器底部压强之比为3:1,求物块A在水中所受的浮力及物块A的质量。
33.一个圆柱形容器放在水平桌面上,如图甲所示,容器中立放着一个均匀实心圆柱体M,现慢慢向容器中加水,加入的水对容器底的压强p水与所加水的质量m的关系如图丙所示,容器足够高,在整个过程中无水溢出,M的底面始终与容器中的水面平行。当加入的水等于3 kg时,物体M刚好漂浮且露出水面的高度为4 cm。如图乙所示(已知ρ水=1.0×103kg/m3,g取10N/kg).
(1)在甲图中画出圆柱体M对容器底部压力示意图。
(2)圆柱体 M 刚好漂浮时容器中水的深度h= cm;圆柱体M 的密度为 kg/m3。
(3)当容器中加入足够多的水后,把一石块放在圆柱体M上,圆柱体刚好浸没,若把石块用一细线系在圆柱体下,石块没碰容器底,如图丁所示,圆柱体露在水面以外的高度为2cm,则石块的密度为多少?(写出必要的文字说明、表达式及最后结果)
34.小欣和小婕在做测量密度的实验。
(1)小欣将天平放在 上,将游码归零,并调节平衡螺母,使指针指到分度盘中央刻度处;
(2)小欣想测量酒精的密度,正确的操作步骤应该是:
A.用天平测出空烧杯的质量记为m1;
B.将酒精全部倒入量筒中,用量筒测出酒精的体积记为V;
C.用天平测出烧杯和酒精的总质量记为m2
(3)在上述B步骤中,量筒的示数如图甲所示,则量筒中酒精的体积为 mL;在上述C步骤中,天平的示数如图乙所示,则烧杯和酒精的总质量为 g。小欣在进行A步骤时,重新对天平进行了调平,调平过程如图丙所示,则小欣测得的酒精密度比真实值将 ;(选填“偏大”、“偏小”或“准确”)
(4)同组的小婕用另外的方法来测量酒精的密度,他取来一块密度为ρ的鹅卵石,利用电子秤继续测量,设计了如下方案:
①先用电子秤测出鹅卵石的质量M1;
②在烧杯中放入适量的酒精将鹅卵石浸没,在液面到达的位置上作标记,用电子秤测出总质量为M2;
③将鹅卵石从酒精中取出,用电子秤测出剩余酒精和烧杯的总质量为M3;
④向烧杯中加酒精到标记处,再用电子秤测出此时酒精和烧杯的总质量为M4。
为了使测出来的酒精密度尽可能的准确,在小明记录的上述数据中,步骤 (选填“①”“②”“③”“④”)记录的数据是多余的,则酒精的密度是 (用测出来的物理量表示);小婕测量完毕之后,取下电子秤上的烧杯发现电子秤的示数并不为0,而是显示为“-0.5g”,则小婕测得的酒精的密度将 (选填“偏大”、“偏小”或“不受影响”)。
35.某水位报警器如图所示:光敏电阻R和光源正对安装在水池侧壁等高处。R接收到光源发出的光时阻值为20Ω,未接收到光时阻值为120Ω。为电阻箱,Q为边长5cm的正方体浮子,密度为0.6g/cm3,当池内水面缓慢上升至某处时,浮子将挡住射向R的光线,报警铃声响起。当线圈中的电流时,铁质开关K被吸上,反之被释放。电源电压,不计线圈电阻,g取10N/kg。
(1)浮子Q缓慢上升时受到的浮力为 N,露出水面的高度为 cm;
(2)如图所示,为保证开始报警时的液面位置MN与R之间高度差,需要对装置进行适当的调整,下列措施可行的是 ;(有多个选项正确)
A.仅换用密度小些的材料制作浮子 B.仅将池内水换为密度小些的液体
C.仅将浮子的边长增大一些 D.仅将浮子做成厚度均匀的空心正方体
(3)在该装置能实现其功能的前提下:
①求电阻箱接入电路的最大值和最小值分别是多少? 、
②在满足①问的条件下,当电路未报警时求光敏电阻R消耗的最小电功率是多少?
③在满足①问的条件下,当电路报警时求光敏电阻R消耗的最大电功率是多少?
答案解析部分
1.A
2.A
3.B
4.静止;不变;小
5.A
6.2.00;34;36.5;同种电荷相互排斥;由B到A;由A到B
7.100.6;1.4
8.116;大于
9.不合理:无法直接测出一根大头针的质量,不能直接测出整包大头针的质量。 改正:用天平测出10(或20)根大头针的质量,记作m,则一根大头针的质量为 ;把这包大头针分成差不多的两份,分别用天平测出其质量为m1、m2;则大头针的数量是 。
使用天平时,所测量的数量不能超量程,天平不能测量微小物体的质量。
10.B
11.D
12.D
13.A
14.(1)解: 水的重力:
(2)解: 可知,水的体积:,
则柱形容器中水的深度:,
则水对容器底部的压强:
(3)解: 因甲、乙底部用一轻质细软管连通组成连通器,把小球放入容器中,当水停止流动时两容器中水面相平,所以水对容器底部压强增加量相同,又因,
由可知,甲容器中水对容器底的压力增加量小,又因为甲、乙容器对地面的压力增加量相等,
由和则水面上升的高度:,
水对乙容器底压强的增加量:,
水对乙容器底压力的增加量:,
因物体对水平面的压力和自身的重力相等,且甲、乙容器对地面的压力增加量相等,所以,,所
以小球的重力:,
则由可知,
实心体的密度:
(1)根据可求出水的重力。
(2)根据可求出水的体积,从而可求出容器内水的深度,根据可求出水对容器底部的压强。
(3)甲、乙的底部用一根轻质细软管连通形成连通器,则水静止时甲、乙容器中水面始终相平,据此得出两容器底受到水压强的增加量关系,根据得出结合得出两容器中水对容器底的压力增加量关系,然后确定小球放入的容器;物体对水平面的压力和自身的重力相等,然后结合甲、乙容器对地面的压力增加量相等得出乙容器对地面的压力增加量,根据求出水面上升的高度,利用和求出水对乙容器底压力的增加量,根据表示出实心小球A的重力,然后得出等式即可求出小球A的密度。
15.变小;变小;低
16.水平;右;43.4;2;8;偏小
17.(1)
(2)偏大
(3)水平;零刻度线;左;左;59.8;40;
(4)加盐
(5)C
18.温度;变大;上调
质量是描述物体所含物质多少的物理量,所以质量是物质一种属性,它不随位置、形状、状态和温度的改变而改变。
汽油也有热胀冷缩的性质,随着气温下降,同等质量的汽油的体积会缩小,汽油的密度会变大。
每吨汽油价格不变,但是因为热胀冷缩,每吨汽油的体积缩小了,要想卖到原来每吨汽油的价格,每升汽油的价格应该上调。
质量是描述物体所含物质多少的物理量,所以质量是物质一种属性,它不随位置、形状、状态和温度的改变而改变。
19.D
20.D
A.由图乙可知,当圆柱体没有浸入水中时,弹簧测力计示数为10N ,此时圆柱体的重力为10N,故A错误;
B.由图乙可知,当圆柱体下降4cm后,弹簧测力计的示数开始减小,说明此时圆柱体的下表面与水面相平,当圆柱体下降8cm后,弹簧测力计的示数不变,说明圆柱体刚好浸没在水中,所以圆柱体的高度为:,故B错误;
C.当圆柱体上表面刚进入水时,即圆柱体浸没在水中时,由图乙可知,圆柱体浸没在水中时,弹簧测力计示数为2N不变,此时圆柱体受到的浮力为:
故C错误;
D.圆柱体浸没在水中时,排开水的体积为:
此时圆柱体的体积等于圆柱体排开水的体积,所以圆柱体的体积为:
圆柱体的质量为:
圆柱体密度为:
故D正确。
故选D。
由图乙可知,圆柱体没有浸入水中时,弹簧测力计的示数等于圆柱体的重力;从圆柱体下表面与水面相平到圆柱体浸没在水中的过程中,弹簧测力计的示数变小,由此可知物体的高度;当圆柱体浸没在水中时,圆柱体的体积等于排开水的体积,根据可求出圆柱体的体积,根据可求出圆柱体的质量,根据求出圆柱体的密度。
21.D
A.根据图丙,物体甲的高度h甲=40cm,
物体甲的重力:G甲=F压甲=pS甲=8000Pa×200×10-4m2=160N,
物体甲的体积:V甲=S甲h甲=200×10-4m2×40×10-2m=8×10-3m3,
计算物体甲的密度:,故A错误;
B.当Δh1=10cm时,切去物体甲的重力
ΔG1=ρ甲gS甲Δh1=2×103kg/m3×10N/kg×200×10-4m2×10×10-2m=40N,
此乙容器压强的变化量Δp=p2-p1=2600Pa-1600Pa=1000Pa,_40N=4×10
容器乙的底面积:,
根据图丙,容器乙的高度为h乙=20cm,
在未放物体甲前,乙容器中水的深度,
原容器中水的质量:m水=ρ水S乙h水=1.0g/cm3×400cm2×15cm=6000g=6kg,
未放物体甲时,乙容器和水的中重力:G=F乙压=p1S乙=1600Pa×4×10-2m2=64N,
未放物体甲时,乙容器和水的质量:
容器乙的质量:m乙=m总-m水=6.4kg-6kg=0.4kg,故B错误;
C.图中a对应的高度为Δh1,乙容器的重力等于对地面的总压力,
F乙总=G乙总=G乙+ρ水g(S乙-S甲) h乙+ρ甲gS甲Δh1,
甲切去Δh1后,甲对地面的压强和容器乙对地面的压强相等,
即,代入数据,解得Δh1=23cm,故C错误;
D.当Δh=20cm时,乙容器对桌面的压强p'=代入数据,解得p'=3100Pa,故D正确。
故选D.
根据物体的压强,利用F=pS计算压力,结合重力,计算物体的质量,利用,计算密度;结合G=mg=ρgSh计算物体的重力,结合压强的变化和压力的关系,计算受力面积;结合压强,根据G=F=pS,计算物体的重力;利用物体的总重力,计算水平面受到的总压力,根据,计算压强。
22.D
23.32;5∶4
计算B物体的质量为:,
则B的重力为:;
同理,计算物体A的质量为:
若A、B对水平地面的压强相等,可以将物体A沿竖直方向切下体积V1叠放到物体B上,也可以将物体A沿水平方向切下体积V2叠放到物体B上,A、B对水平地面的压强相等,即
分别计算A、B的底面积为,
当A竖直切,切去的质量为m1时,根据,A对地面的压强不变,则,
即,代入数据得,解得
若A水平切,切去的质量为m2时,,即,
代入数据得:,解得,
则。
根据m=ρV,计算物体的质量;利用G=mg,计算重力;根据,计算压强,结合切割后压强相等,计算质量;根据,计算体积。
24.2:9
设冰山的质量为m,根据密度公式有体积;根据重力公式有重力G=mg;由于冰山漂浮在海水中,所以根据物体浮沉条件,可知冰山所受浮力为F浮=G=mg;根据阿基米德原理有,即冰山在海面下的体积为,则,所以。
根据密度公式,可表示出冰山的体积;根据重力公式、物体浮沉条件以及阿基米德原理,可表示出冰山在海面下的体积。
25.0.9;
26.(1)解:由图乙可知,当h0=0cm时,力传感器的示数为F0=8N,由细杆的质量不考虑可知,正方体A对力传感器的压力等于自身的重力,即正方体A的重力为
(2)解:正方体A刚好完全浸没时,水对容器底的压强为
(3)解:当水深10cm时正方体A下端恰好接触水面,可知杆的长度为
当水深为20cm时,正方体A刚好完全浸没,则正方体A的边长为
正方体A的体积为
由
可知,正方体A的密度为
(4)解:当水深h'=13cm时,A排开水的体积为
此时A受到的浮力为
力传感器的示数为
(1)根据水平面受到的压力,判断物体的重力;
(2)利用p=ρgh,计算液体压强的大小;
(3)根据,可以计算物体的的密度;
(4)根据F浮=ρ液gV排,计算物体受到的浮力的大小,结合物体的重力,计算水平面受到的压力。
(1)由图乙可知,当h0=0cm时,力传感器的示数为F0=8N,由细杆的质量不考虑可知,正方体A对力传感器的压力等于自身的重力,即正方体A的重力为
(2)正方体A刚好完全浸没时,水对容器底的压强为
(3)当水深10cm时正方体A下端恰好接触水面,可知杆的长度为
当水深为20cm时,正方体A刚好完全浸没,则正方体A的边长为
正方体A的体积为
由
可知,正方体A的密度为
(4)当水深h'=13cm时,A排开水的体积为
此时A受到的浮力为
力传感器的示数为
27.A
因梯形物体浸没在水中,则梯形物体受到水的浮力:F浮=ρV排g=ρVg,梯形物体下表面受到水的压强:p下表面=ρgH,梯形物体下表面受到水的压力:F下表面=p下表面S'=ρgHS',因F浮=F下表面-F上表面,所以,梯形物体受到水向下的压力:F上表面=F下表面-F浮=ρgHS'-ρVg=ρg(HS'-V) ,A符合题意,BC不符合题意;梯形物体上底面受到水向下的压力,同时斜面受到水的压力有向下的分力,则F上表面≠p上表面S"=ρg(H-h) S",D不符合题意。
故答案为:A.
利用F浮=ρgV排,计算梯形物体受到的浮力;根据p=ρhg计算梯形物体下表面受到水的压强,利用F=pS计算下表面受到水的压力,最后根据F浮=F下表面-F上表面,计算该物体受到水向下的压力;梯形物体上底面受到水向下的压力,同时斜面受到水的压力有向下的分力,故不能用上底面受到的压强计算压力。
28.D
29.B
A.根据图2可知,甲的密度为:;
乙的密度为:;
则二者的密度之比为:ρ甲:ρ乙=7.2×103kg/m3:2.7×103kg/m3=8:3,故A错误,B正确;
C. 若边长之比, 根据p=ρgh可知,对地面的压强之比:p甲:p乙=ρ甲h甲:ρ乙h乙=(8×1):(3×4)=2:3,故C错误;
D.若边长之比, 根据G=mg=ρVg可知,二者的重力之比:G甲:G乙=ρ甲V甲:ρ乙V乙=(8×13):(3×43)=1:24,故D错误。
故选B。
AB.上下密=度均匀的柱体对地面的压强:;
CD.根据p=ρgh计算压强之比,根据G=mg=ρVg计算二者的重力之比。
30.100;5∶13
31.小于;;偏大
32.(1)30N;(2)2500Pa;(3)
33.(1)
(2)6;
(3)解:3kg水的体积
圆柱体周围的水的底面积
由于加入的水等于7kg与3kg时压强分别为 ,
由 得
圆柱体的底面积S圆柱体=S-S水=0.1m2=0.05m2=0.05m2
则圆柱体的体积V=sh=0.005m2
圆柱体M的重力30N
密度
(1)圆柱体M对容器底部的压力作用在二者的接触面上方向竖直向下,如下图所示:
(2)①根据图片可知,当加入的水m水=3kg时,此时水的压强p水=0.6×103Pa,
由于此时图像出现拐点,因此圆柱体漂浮在水面上,
由p=ρ液gh可得,此时水的深度:;
②由于物体M刚好漂浮且露出水面的高度为4cm,
则物体M的高度H=h+h露=6cm+4cm=10cm;
由漂浮条件可知:F浮=G,
即:ρ水V排g=ρ物V物g,
则ρ水Sh浸g=ρ物SHg,
ρ水h浸=ρ物H,
1×103 kg/m3×6cm=ρ物×10cm;
解得:ρ物=0.6×103kg/m3。
(3)① 加入3kg水的体积 ;
而圆柱体的此时进入水中深度为6cm,
则圆柱体周围的水的底面积: ;
由于加入的水等于7kg与3kg时压强分别为 ,
由 得:
容器的底面积 ;
圆柱体的底面积S圆柱体=S-S水=0.1m2-0.05m2=0.05m2;
圆柱体的高度为h=10cm,
则圆柱体的体积V=sh=0.05m2×0.1m=0.005m3;
那么圆柱体M的重力G=mg=ρVg=0.6×103kg/m3×10N/kg×0.005m3=30N;
②当圆柱体完全浸没时受到的浮力:F浮=ρ液gV排=1×103kg/m3×10N/kg×0.005m3=50N;
则石块的重力:G石块=F浮力-G=50N-30N=20N;
当石块用细线系在圆柱体下面时,它们仍然处于漂浮状态,则受到的浮力不变,那么排开水的总体积不变,因此圆柱体露出水面的体积恰好等于石块的体积,
则石块的体积V石=V露=Sh露=0.05m2×0.02m=0.001m3;
则石块的密度: .
(1)确定压力的大小、方向和作用点,然后沿力的方向画一条带箭头的线段即可;
(2)①当圆柱体漂浮前,由于圆柱体占有一定体积,因此水面上升较快,压强增大较快。当圆柱体漂浮后,圆柱体不再占有下面水的体积,因此水面上上较慢,压强增大较慢。据此确定圆柱体漂浮时容器底部受到水的压强,再根据液体压强公式p=ρ液gh就计算容器中水的深度。
②当圆柱体刚刚漂浮时,圆柱体进入水中的深度等于此时水的深度,再与露出水的长度相加得到圆柱体的高度。根据浮沉条件,结合阿基米德原理,重力公式列出放出,进而计算出M的密度。
(3)当加入3kg水,圆柱体刚好漂浮,但是还未离开底部。根据计算出加水的体积,根据计算出圆柱体周围水的底面积。
当圆柱体漂浮后,容器底部增大的压力就等于增加水的重力,根据图片确定加水3kg和7kg时水对容器底部的压强,根据 计算出容器的底面积。
圆柱体的底面积等于容器的底面积减去周围水的底面积,接下来根据V=Sh计算出圆柱体的体积,根据G=mg=ρgV计算圆柱体的重力。
当圆柱体完全浸没时,根据阿基米德原理F浮=ρ液gV排计算出M和石块受到的总浮力,再根据二力平衡的条件G石块=F浮力-G计算石块的重力。
将石块用细线系在圆柱体下面时,它们仍然处于漂浮状态,则受到的浮力不变,那么排开水的总体积不变,因此圆柱体露出水面的体积恰好等于石块的体积,即V石=V露出。最后根据密度公式计算即可。
34.水平台面;CBA;30;130.4;偏小;③;;偏小
35.0.75;2;ACD;280Ω;180Ω;0.032W;0.192W
一、质量
1.义务教育物理课程体现了“从生活走向物理,从物理走向社会”的理念,贴近大家的生活。下列对生活中物理量的估计,与实际最接近的是( )
A.乒乓球被誉为我国的“国球”,其直径约为40mm
B.人的脉搏跳动一次的时间约为10s
C.一瓶矿泉水的质量约为55g
D.正常人的体温约为38.5℃
2.一个初中学生的质量最接近于( )
A.50千克 B.500千克 C.50牛 D.500牛
3.物理在生活中无处不在,下列关于在教室里的物理现象分析错误的是( )
A.利用电子白板讲题时,老师应关掉白板上方的灯,避免干扰学生看白板上的内容
B.老师在教室里讲话时听不到回声是因为教室里没有回声
C.冬天教室窗玻璃起雾,雾在教室内侧的玻璃上
D.老师用粉笔在黑板上书写后,粉笔的质量变小
4.遨游九天,筑梦苍穹,中国人对太空的探索永不止步。2024年10月30日,神舟十九号 载人飞船成功发射并与天和核心舱形成组合体(如图所示),乘组顺利进驻中国空间站。神舟十九号飞船发射时,以神舟十九号中的航天员为参照物,神舟十九号飞船是 的,航天员从地面来到空间站内,其质量 (填变化情况);航天器的外壳要求轻巧、耐高温,那么用来制造航天器外壳的材料应具有的特性是:密度 且熔点高。
二、质量的测量
5.用天平测完物体质量后,发现左盘上黏有一小块橡皮泥。下列分析正确的是( )
A.若橡皮泥是在调横梁水平前黏上去的,则测量结果仍然准确
B.若橡皮泥是在调横梁水平后黏上去的,则测出的质量小于物体的真实质量
C.橡皮泥无论是在什么时候黏上去的,测量结果都不准确
D.如果橡皮泥质量较小,对天平的测量不会起什么作用
6.(1)如图1甲所示,图甲中木块的长度为 cm,天平平衡时,放在天平右盘中的砝码和游码的位置如图1乙所示 g;图1丙中的体温计示数是 ℃。
(2)两个相同的验电器A和B,用与毛皮摩擦过的橡胶棒接触验电器A的金属球,验电器A的金属箔张开的原因是 ,另一个验电器B不带电(如图2甲所示)。用带手柄的金属杆把A和B连接起来,验电器B的金属箔张开(如图2乙所示),金属杆中瞬间电流方向是从 ,自由电子定向移动方向是 (后两空选填“由A到B”或“由B到A”)。
7.某同学分别做了如图所示的测量,则甲图中物体质量为 g;乙图中弹簧测力计读数为 N。
8.用托盘天平称物体质量时将被测物和砝码放错了位置,天平平衡时,左盘放100g和20g的砝码各一个,游码所对的刻度值为4g,则物体质量为 g。测完后才发现使用的砝码已经磨损了,则物体质量的测量值 (选填“大于”、“等于”或“小于”)真实值。
9.以下是小明利用一称量为200g的天平测量一包大头针(约350g)数量的实验方案:先用天平直接测出一根大头针的质量为m,然后用天平直接测出整包大头针的质量为m总,最后根据m总/m求出大头针的数量。请指出小明做得不合理或有误的地方并改正.
三、密度
10.如图所示,在测量铝块密度的实验中,,下列说法正确的是( )
A.测量过程中可以移动平衡螺母将天平调平
B.铝块是空心的
C.所测铝块的质量为52.4g
D.如果把铝块打磨掉一部分铝屑,则剩余铝块密度将不变
11.下列物理量的符号和国际单位,对应错误的是( )
A.速度v-m/s B.质量m-kg
C.密度ρ-kg/m3 D.功率P-J
12.杯中的某种溶液,倒掉一半后,对剩下的半杯溶液描述不正确的是
A.热值不变 B.密度不变 C.质量减半 D.比热容减半
13.两个实心物体a、b的体积与质量的关系如图所示.下列说法正确的是( )
A.a的密度是b的密度的2倍
B.b的密度是a的密度的2倍
C.a的密度是0.5×103kg/m3
D.a、b的密度与它们的质量、体积有关
14.如图所示,盛有60kg水的柱形容器甲、乙置于水平地面上,容器足够高,两容器底部用软细管(体积忽略不计)连通。已知甲、乙容器底面积分别为、,,。求:
(1)水的重力;
(2)水对容器底部的压强;
(3)小明将体积为的实心体A浸没在甲或乙容器中,整个过程中水未溢出,A静止后沉底,小明发现甲、乙容器对地面的压力增加量相等。请判断小明是把A放入甲容器还是乙容器中,并计算出实心体A的密度。
15.如图所示,是登山爱好者从小型氧气罐里吸取氧气的情景,当氧气罐里氧气被吸取部分后,罐内氧气的质量将 ,密度将 (均选填“变大”、“变小”或“不变”)。当他到达山顶时,他发现密封的零食包装袋鼓起来了,这是因为山顶上的气压比山脚下的气压 造成的。
16.小薇同学在测固体密度时,操作步骤如下:
(1)在实验室,小薇把天平放在 工作台上,将游码归零,发现指针偏向分度盘的左侧,此时应将平衡螺母向 调节(选填“左”或“右”),使天平横梁平衡;
(2)小薇选用了一块小矿石,用调好的天平测它的质量,当右盘中所加砝码和游码的位置如图甲所示时,天平恢复平衡,则测得的矿石质量是 g;
(3)如图乙所示的量筒分度值为 cm3,在量筒中装入适量的水,将系了细线的矿石轻放入量筒,如图乙所示,测得矿石的体积是 cm3;
(4)实验后,小薇发现使用的20g砝码生锈了,由此导致测得的矿石密度会 (选填“偏大”“偏小”或“不变”)。
17.课外兴趣小组需要密度为的盐水,为检验配制的盐水是否合格。
(1)小蓬设计了如下方案:
①用天平测出空烧杯的质量;
②往烧杯中倒入适量盐水,测出烧杯和盐水的总质量;
③将烧杯中的盐水倒入量筒中,测出盐水的体积V;
④则盐水的密度 ;
(2)经分析该方案会使密度测量结果 (选填“偏大”或“偏小”);
(3)小组成员改进了实验方案并进行了如下操作:
将天平放在 桌面上,将游码移至标尺左端的 上,发现指针的位置如图甲所示,则需将平衡螺母向 调节。往烧杯中倒入适量盐水,将烧杯放在天平的 盘,测出烧杯和盐水的总质量为 g;将烧杯中的部分盐水倒入量筒中,如图丙读出盐水的体积为 ;测出烧杯和剩余盐水的质量为15g;计算出盐水的密度为 ;
(4)为配制合格的盐水,需要继续向盐水中 (选填“加盐”或“加水”);
(5)小蓬接着测量了不同体积的牛奶的质量,描绘出质量与体积关系的图线如丙图中A所示。她分析后发现,由于误将烧杯和水的总质量当作了水的质量,导致图线A未经过坐标原点,由此推断:水的质量与体积关系的图线应是 (选填丙图中“B”、“C”或“D”)。
18.质量是物质一种属性,它不随位置、形状、状态和 的改变而改变。近几个月份的汽油价格进行了调整。和大多数物质一样,汽油也有热胀冷缩的性质,随着气温的下降,汽油密度会 (选填“变大”或“变小”),受此因素影响,在每吨汽油价格不变的情况下,每升(每立方分米)汽油的价格会 (选填“上调”或“下调”)。
四、能力提升
19.弹簧测力计下挂一长方体物体,将物体从盛有适量水的烧杯(可看成柱形)上方离水面某一高度处缓缓下降,然后将其逐渐浸入水中,如图甲;图乙是弹簧测力计示数与物体下降高度变化关系的图像,则下列说法错误的是( )
A.物体的体积是
B.物体的密度是
C.物体刚浸没时下表面受到水的压力是4N
D.物体完全浸没后与最初时相比,烧杯底部受到水的压力增大了5N
20.如图甲,用弹簧测力计悬挂的圆柱体缓慢浸入盛水的烧杯中,直至圆柱体浸没在水中,整个过程中弹簧测力计示数F与圆柱体下降高度h变化关系的图像如图乙所示,忽略液面的高度变化,以下判断正确的是( )
A.圆柱体受到重力为8N
B.圆柱体的高度为8cm
C.圆柱体上表面刚进入水时受到浮力为2N
D.圆柱体的密度为1.25×103kg/m3
21.如图所示,质量分布均匀、底面积为200cm2的长方体甲和质量未知的薄壁柱形容器乙放置于水平地面上,已知容器乙的高度为h,其内装有一定量的水。现将甲沿水平方向切去一定的厚度△h,并将甲切下的部分保持竖直轻放入乙容器中,甲、乙对地面的压强随切去厚度△h的变化情况如图丙所示,则下列说法正确的是
A.甲的密度为 200kg/m3
B.乙容器的质量为 2.4kg
C.图丙中 a的值为21cm
D. h=20cm时, 乙容器对桌面的压强为 3100Pa
22.某同学用托盘天平和量筒测量一小石块的密度,如图甲是调节天平时的情形,图乙和图丙分别是测量石块质量和体积时的情形,下列说法正确的是( )
A.甲图中应将平衡螺母向右调,使横梁平衡
B.乙图中测石块质量时,天平的读数是71.2g
C.由丙图量筒的示数测得石块的体积是
D.计算出石块的密度是
23.如图所示,边长分别为0.4m和0.2m的实心正方体A、B放置在水平地面上,A的密度为0.6×103kg/m3,B的密度为0.4×103kg/m3,物体B的重力为 N。为使A、B对水平地面的压强相等,可以将物体A沿竖直方向切下体积V1叠放到物体B上,也可以将物体A沿水平方向切下体积V2叠放到物体B上,则V1与V2之比为 。
24.冰山露出海面的部分只是冰山的一小部分,所以常有“冰山一角”的说法。若海水的密度是 1.1×103kg/m3,冰的密度是 0.9×103kg/m3,则冰山露出海面的体积与海面下的体积之比是 。
25.水平放置的电子秤上有一质量300g、底面积400cm2的长方体薄壁柱形容器,容器内装有一定量的某液体。将质量为900g的实心正方体轻放入液体中,稳定后如图甲所示。打开容器底部的阀门向外排放液体,排放过程中,容器底部所受液体压强与排出液体体积的关系如图乙所示,正方体的密度为 ,当电子秤示数变化2000g时,液体对容器底的压强与容器对电子秤的压强之比为 。
26.小明同学利用力学传感器设计了如图甲所示的装置,竖直细杆B的下端通过力传感器(小方块)固定在容器底部,上端与实心正方体A固定。细杆B长10cm,A不吸水。不计细杆B及连接处的质量和体积。力传感器可以显示出细杆B受到作用力的大小,现缓慢向容器中加水,当水深为20cm时正方体A刚好完全浸没。力传感器的示数大小F随水深h变化的图像如图乙所示。
(,g取)求:
(1)正方体A的重力;
(2)正方体A刚好完全浸没时,水对容器底的压强;
(3)正方体A的密度;
(4)当容器内水的深度为13cm时,正方体A所受浮力的大小及力传感器的示数大小。
五、直击中考
27.如图所示,有一个梯形物体浸没在某种液体中(物体与容器底不紧密接触),容器液面上方近似为真空,液体的密度为ρ,深度为H,物体高度为h,体积为V,较大的下底面面积为S',较小的上底面面积为S",容器的底面面积为S,则该物体受到水向下的压力F等于( )
A.ρg(HS'-V) B.ρgV-ρghS' C.ρghS'-ρgV D.ρg(H-h)S"
28.如图甲中,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中。图乙是钢绳拉力随时间变化的图象。g取10N/kg,水的密度为,若不计水的阻力,下列说法错误的是( )
A.石料的质量为250kg
B.石料的密度为
C.石料所受浮力随石料浸入水中体积的增大而增大
D.石料浸没水中后受到的浮力为1500N且保持不变
29.如图1所示,甲、乙两质地均匀的正方体放在水平地面上,图2为它们对地面的压强与其边长的关系图,g取,下列说法正确的是( )
A.甲物体的密度为
B.甲、乙物体的密度之比为8∶3
C.若边长之比,则对地压强之比
D.若边长之比,则所受重力之比
30.如图所示,长方体物块A重为8N、底面积为40cm2,高为10cm,质量不计的细杆上端固定在天花板上、下端与物块A的上表面相连,足够高的柱形容器重为2N。现向容器中缓慢注水1.8kg,此时水面高20cm,A浸入水中的体积为其总体积的一半,容器的底面积为 ;若将A的左、右两侧沿竖直方向各切掉总体积的四分之一,并将切掉部分放入柱形容器中,此时水对容器底部的压强改变量为,容器对桌面的压强改变量为,则 。
31.雪在外力挤压下可形成冰,表明雪的密度 冰的密度,(选填“大于”、“等于”或“小于”)。小华利用冰的密度(ρ冰),使用如下方法来估测积雪的密度:利用平整地面上的积雪,脚向下用力踩在雪上,将雪踏实成冰并形成一个下凹的脚印,然后测量脚印的深度h和积雪原来的厚度H,就可以估测出积雪的密度,并写出雪的密度的表达式: (用已知物理量符号表示)。若实验时雪没有踩踏实,则所测雪的密度将 (选填“偏大”、“偏小”或“不变”)。
32.如图所示,体积为的正方体物体A水平放置,其密度大于水的密度。另有一足够高的薄壁柱形容器B置于水平地面,底面积为,质量为3kg。(,)
(1)求容器的重力;
(2)向容器B注入体积为的水时,求容器对水平地面的压强;
(3)在(2)问的前提下,再将物体A放入容器中,此时容器对地面的压强与水对容器底部压强之比为3:1,求物块A在水中所受的浮力及物块A的质量。
33.一个圆柱形容器放在水平桌面上,如图甲所示,容器中立放着一个均匀实心圆柱体M,现慢慢向容器中加水,加入的水对容器底的压强p水与所加水的质量m的关系如图丙所示,容器足够高,在整个过程中无水溢出,M的底面始终与容器中的水面平行。当加入的水等于3 kg时,物体M刚好漂浮且露出水面的高度为4 cm。如图乙所示(已知ρ水=1.0×103kg/m3,g取10N/kg).
(1)在甲图中画出圆柱体M对容器底部压力示意图。
(2)圆柱体 M 刚好漂浮时容器中水的深度h= cm;圆柱体M 的密度为 kg/m3。
(3)当容器中加入足够多的水后,把一石块放在圆柱体M上,圆柱体刚好浸没,若把石块用一细线系在圆柱体下,石块没碰容器底,如图丁所示,圆柱体露在水面以外的高度为2cm,则石块的密度为多少?(写出必要的文字说明、表达式及最后结果)
34.小欣和小婕在做测量密度的实验。
(1)小欣将天平放在 上,将游码归零,并调节平衡螺母,使指针指到分度盘中央刻度处;
(2)小欣想测量酒精的密度,正确的操作步骤应该是:
A.用天平测出空烧杯的质量记为m1;
B.将酒精全部倒入量筒中,用量筒测出酒精的体积记为V;
C.用天平测出烧杯和酒精的总质量记为m2
(3)在上述B步骤中,量筒的示数如图甲所示,则量筒中酒精的体积为 mL;在上述C步骤中,天平的示数如图乙所示,则烧杯和酒精的总质量为 g。小欣在进行A步骤时,重新对天平进行了调平,调平过程如图丙所示,则小欣测得的酒精密度比真实值将 ;(选填“偏大”、“偏小”或“准确”)
(4)同组的小婕用另外的方法来测量酒精的密度,他取来一块密度为ρ的鹅卵石,利用电子秤继续测量,设计了如下方案:
①先用电子秤测出鹅卵石的质量M1;
②在烧杯中放入适量的酒精将鹅卵石浸没,在液面到达的位置上作标记,用电子秤测出总质量为M2;
③将鹅卵石从酒精中取出,用电子秤测出剩余酒精和烧杯的总质量为M3;
④向烧杯中加酒精到标记处,再用电子秤测出此时酒精和烧杯的总质量为M4。
为了使测出来的酒精密度尽可能的准确,在小明记录的上述数据中,步骤 (选填“①”“②”“③”“④”)记录的数据是多余的,则酒精的密度是 (用测出来的物理量表示);小婕测量完毕之后,取下电子秤上的烧杯发现电子秤的示数并不为0,而是显示为“-0.5g”,则小婕测得的酒精的密度将 (选填“偏大”、“偏小”或“不受影响”)。
35.某水位报警器如图所示:光敏电阻R和光源正对安装在水池侧壁等高处。R接收到光源发出的光时阻值为20Ω,未接收到光时阻值为120Ω。为电阻箱,Q为边长5cm的正方体浮子,密度为0.6g/cm3,当池内水面缓慢上升至某处时,浮子将挡住射向R的光线,报警铃声响起。当线圈中的电流时,铁质开关K被吸上,反之被释放。电源电压,不计线圈电阻,g取10N/kg。
(1)浮子Q缓慢上升时受到的浮力为 N,露出水面的高度为 cm;
(2)如图所示,为保证开始报警时的液面位置MN与R之间高度差,需要对装置进行适当的调整,下列措施可行的是 ;(有多个选项正确)
A.仅换用密度小些的材料制作浮子 B.仅将池内水换为密度小些的液体
C.仅将浮子的边长增大一些 D.仅将浮子做成厚度均匀的空心正方体
(3)在该装置能实现其功能的前提下:
①求电阻箱接入电路的最大值和最小值分别是多少? 、
②在满足①问的条件下,当电路未报警时求光敏电阻R消耗的最小电功率是多少?
③在满足①问的条件下,当电路报警时求光敏电阻R消耗的最大电功率是多少?
答案解析部分
1.A
2.A
3.B
4.静止;不变;小
5.A
6.2.00;34;36.5;同种电荷相互排斥;由B到A;由A到B
7.100.6;1.4
8.116;大于
9.不合理:无法直接测出一根大头针的质量,不能直接测出整包大头针的质量。 改正:用天平测出10(或20)根大头针的质量,记作m,则一根大头针的质量为 ;把这包大头针分成差不多的两份,分别用天平测出其质量为m1、m2;则大头针的数量是 。
使用天平时,所测量的数量不能超量程,天平不能测量微小物体的质量。
10.B
11.D
12.D
13.A
14.(1)解: 水的重力:
(2)解: 可知,水的体积:,
则柱形容器中水的深度:,
则水对容器底部的压强:
(3)解: 因甲、乙底部用一轻质细软管连通组成连通器,把小球放入容器中,当水停止流动时两容器中水面相平,所以水对容器底部压强增加量相同,又因,
由可知,甲容器中水对容器底的压力增加量小,又因为甲、乙容器对地面的压力增加量相等,
由和则水面上升的高度:,
水对乙容器底压强的增加量:,
水对乙容器底压力的增加量:,
因物体对水平面的压力和自身的重力相等,且甲、乙容器对地面的压力增加量相等,所以,,所
以小球的重力:,
则由可知,
实心体的密度:
(1)根据可求出水的重力。
(2)根据可求出水的体积,从而可求出容器内水的深度,根据可求出水对容器底部的压强。
(3)甲、乙的底部用一根轻质细软管连通形成连通器,则水静止时甲、乙容器中水面始终相平,据此得出两容器底受到水压强的增加量关系,根据得出结合得出两容器中水对容器底的压力增加量关系,然后确定小球放入的容器;物体对水平面的压力和自身的重力相等,然后结合甲、乙容器对地面的压力增加量相等得出乙容器对地面的压力增加量,根据求出水面上升的高度,利用和求出水对乙容器底压力的增加量,根据表示出实心小球A的重力,然后得出等式即可求出小球A的密度。
15.变小;变小;低
16.水平;右;43.4;2;8;偏小
17.(1)
(2)偏大
(3)水平;零刻度线;左;左;59.8;40;
(4)加盐
(5)C
18.温度;变大;上调
质量是描述物体所含物质多少的物理量,所以质量是物质一种属性,它不随位置、形状、状态和温度的改变而改变。
汽油也有热胀冷缩的性质,随着气温下降,同等质量的汽油的体积会缩小,汽油的密度会变大。
每吨汽油价格不变,但是因为热胀冷缩,每吨汽油的体积缩小了,要想卖到原来每吨汽油的价格,每升汽油的价格应该上调。
质量是描述物体所含物质多少的物理量,所以质量是物质一种属性,它不随位置、形状、状态和温度的改变而改变。
19.D
20.D
A.由图乙可知,当圆柱体没有浸入水中时,弹簧测力计示数为10N ,此时圆柱体的重力为10N,故A错误;
B.由图乙可知,当圆柱体下降4cm后,弹簧测力计的示数开始减小,说明此时圆柱体的下表面与水面相平,当圆柱体下降8cm后,弹簧测力计的示数不变,说明圆柱体刚好浸没在水中,所以圆柱体的高度为:,故B错误;
C.当圆柱体上表面刚进入水时,即圆柱体浸没在水中时,由图乙可知,圆柱体浸没在水中时,弹簧测力计示数为2N不变,此时圆柱体受到的浮力为:
故C错误;
D.圆柱体浸没在水中时,排开水的体积为:
此时圆柱体的体积等于圆柱体排开水的体积,所以圆柱体的体积为:
圆柱体的质量为:
圆柱体密度为:
故D正确。
故选D。
由图乙可知,圆柱体没有浸入水中时,弹簧测力计的示数等于圆柱体的重力;从圆柱体下表面与水面相平到圆柱体浸没在水中的过程中,弹簧测力计的示数变小,由此可知物体的高度;当圆柱体浸没在水中时,圆柱体的体积等于排开水的体积,根据可求出圆柱体的体积,根据可求出圆柱体的质量,根据求出圆柱体的密度。
21.D
A.根据图丙,物体甲的高度h甲=40cm,
物体甲的重力:G甲=F压甲=pS甲=8000Pa×200×10-4m2=160N,
物体甲的体积:V甲=S甲h甲=200×10-4m2×40×10-2m=8×10-3m3,
计算物体甲的密度:,故A错误;
B.当Δh1=10cm时,切去物体甲的重力
ΔG1=ρ甲gS甲Δh1=2×103kg/m3×10N/kg×200×10-4m2×10×10-2m=40N,
此乙容器压强的变化量Δp=p2-p1=2600Pa-1600Pa=1000Pa,_40N=4×10
容器乙的底面积:,
根据图丙,容器乙的高度为h乙=20cm,
在未放物体甲前,乙容器中水的深度,
原容器中水的质量:m水=ρ水S乙h水=1.0g/cm3×400cm2×15cm=6000g=6kg,
未放物体甲时,乙容器和水的中重力:G=F乙压=p1S乙=1600Pa×4×10-2m2=64N,
未放物体甲时,乙容器和水的质量:
容器乙的质量:m乙=m总-m水=6.4kg-6kg=0.4kg,故B错误;
C.图中a对应的高度为Δh1,乙容器的重力等于对地面的总压力,
F乙总=G乙总=G乙+ρ水g(S乙-S甲) h乙+ρ甲gS甲Δh1,
甲切去Δh1后,甲对地面的压强和容器乙对地面的压强相等,
即,代入数据,解得Δh1=23cm,故C错误;
D.当Δh=20cm时,乙容器对桌面的压强p'=代入数据,解得p'=3100Pa,故D正确。
故选D.
根据物体的压强,利用F=pS计算压力,结合重力,计算物体的质量,利用,计算密度;结合G=mg=ρgSh计算物体的重力,结合压强的变化和压力的关系,计算受力面积;结合压强,根据G=F=pS,计算物体的重力;利用物体的总重力,计算水平面受到的总压力,根据,计算压强。
22.D
23.32;5∶4
计算B物体的质量为:,
则B的重力为:;
同理,计算物体A的质量为:
若A、B对水平地面的压强相等,可以将物体A沿竖直方向切下体积V1叠放到物体B上,也可以将物体A沿水平方向切下体积V2叠放到物体B上,A、B对水平地面的压强相等,即
分别计算A、B的底面积为,
当A竖直切,切去的质量为m1时,根据,A对地面的压强不变,则,
即,代入数据得,解得
若A水平切,切去的质量为m2时,,即,
代入数据得:,解得,
则。
根据m=ρV,计算物体的质量;利用G=mg,计算重力;根据,计算压强,结合切割后压强相等,计算质量;根据,计算体积。
24.2:9
设冰山的质量为m,根据密度公式有体积;根据重力公式有重力G=mg;由于冰山漂浮在海水中,所以根据物体浮沉条件,可知冰山所受浮力为F浮=G=mg;根据阿基米德原理有,即冰山在海面下的体积为,则,所以。
根据密度公式,可表示出冰山的体积;根据重力公式、物体浮沉条件以及阿基米德原理,可表示出冰山在海面下的体积。
25.0.9;
26.(1)解:由图乙可知,当h0=0cm时,力传感器的示数为F0=8N,由细杆的质量不考虑可知,正方体A对力传感器的压力等于自身的重力,即正方体A的重力为
(2)解:正方体A刚好完全浸没时,水对容器底的压强为
(3)解:当水深10cm时正方体A下端恰好接触水面,可知杆的长度为
当水深为20cm时,正方体A刚好完全浸没,则正方体A的边长为
正方体A的体积为
由
可知,正方体A的密度为
(4)解:当水深h'=13cm时,A排开水的体积为
此时A受到的浮力为
力传感器的示数为
(1)根据水平面受到的压力,判断物体的重力;
(2)利用p=ρgh,计算液体压强的大小;
(3)根据,可以计算物体的的密度;
(4)根据F浮=ρ液gV排,计算物体受到的浮力的大小,结合物体的重力,计算水平面受到的压力。
(1)由图乙可知,当h0=0cm时,力传感器的示数为F0=8N,由细杆的质量不考虑可知,正方体A对力传感器的压力等于自身的重力,即正方体A的重力为
(2)正方体A刚好完全浸没时,水对容器底的压强为
(3)当水深10cm时正方体A下端恰好接触水面,可知杆的长度为
当水深为20cm时,正方体A刚好完全浸没,则正方体A的边长为
正方体A的体积为
由
可知,正方体A的密度为
(4)当水深h'=13cm时,A排开水的体积为
此时A受到的浮力为
力传感器的示数为
27.A
因梯形物体浸没在水中,则梯形物体受到水的浮力:F浮=ρV排g=ρVg,梯形物体下表面受到水的压强:p下表面=ρgH,梯形物体下表面受到水的压力:F下表面=p下表面S'=ρgHS',因F浮=F下表面-F上表面,所以,梯形物体受到水向下的压力:F上表面=F下表面-F浮=ρgHS'-ρVg=ρg(HS'-V) ,A符合题意,BC不符合题意;梯形物体上底面受到水向下的压力,同时斜面受到水的压力有向下的分力,则F上表面≠p上表面S"=ρg(H-h) S",D不符合题意。
故答案为:A.
利用F浮=ρgV排,计算梯形物体受到的浮力;根据p=ρhg计算梯形物体下表面受到水的压强,利用F=pS计算下表面受到水的压力,最后根据F浮=F下表面-F上表面,计算该物体受到水向下的压力;梯形物体上底面受到水向下的压力,同时斜面受到水的压力有向下的分力,故不能用上底面受到的压强计算压力。
28.D
29.B
A.根据图2可知,甲的密度为:;
乙的密度为:;
则二者的密度之比为:ρ甲:ρ乙=7.2×103kg/m3:2.7×103kg/m3=8:3,故A错误,B正确;
C. 若边长之比, 根据p=ρgh可知,对地面的压强之比:p甲:p乙=ρ甲h甲:ρ乙h乙=(8×1):(3×4)=2:3,故C错误;
D.若边长之比, 根据G=mg=ρVg可知,二者的重力之比:G甲:G乙=ρ甲V甲:ρ乙V乙=(8×13):(3×43)=1:24,故D错误。
故选B。
AB.上下密=度均匀的柱体对地面的压强:;
CD.根据p=ρgh计算压强之比,根据G=mg=ρVg计算二者的重力之比。
30.100;5∶13
31.小于;;偏大
32.(1)30N;(2)2500Pa;(3)
33.(1)
(2)6;
(3)解:3kg水的体积
圆柱体周围的水的底面积
由于加入的水等于7kg与3kg时压强分别为 ,
由 得
圆柱体的底面积S圆柱体=S-S水=0.1m2=0.05m2=0.05m2
则圆柱体的体积V=sh=0.005m2
圆柱体M的重力30N
密度
(1)圆柱体M对容器底部的压力作用在二者的接触面上方向竖直向下,如下图所示:
(2)①根据图片可知,当加入的水m水=3kg时,此时水的压强p水=0.6×103Pa,
由于此时图像出现拐点,因此圆柱体漂浮在水面上,
由p=ρ液gh可得,此时水的深度:;
②由于物体M刚好漂浮且露出水面的高度为4cm,
则物体M的高度H=h+h露=6cm+4cm=10cm;
由漂浮条件可知:F浮=G,
即:ρ水V排g=ρ物V物g,
则ρ水Sh浸g=ρ物SHg,
ρ水h浸=ρ物H,
1×103 kg/m3×6cm=ρ物×10cm;
解得:ρ物=0.6×103kg/m3。
(3)① 加入3kg水的体积 ;
而圆柱体的此时进入水中深度为6cm,
则圆柱体周围的水的底面积: ;
由于加入的水等于7kg与3kg时压强分别为 ,
由 得:
容器的底面积 ;
圆柱体的底面积S圆柱体=S-S水=0.1m2-0.05m2=0.05m2;
圆柱体的高度为h=10cm,
则圆柱体的体积V=sh=0.05m2×0.1m=0.005m3;
那么圆柱体M的重力G=mg=ρVg=0.6×103kg/m3×10N/kg×0.005m3=30N;
②当圆柱体完全浸没时受到的浮力:F浮=ρ液gV排=1×103kg/m3×10N/kg×0.005m3=50N;
则石块的重力:G石块=F浮力-G=50N-30N=20N;
当石块用细线系在圆柱体下面时,它们仍然处于漂浮状态,则受到的浮力不变,那么排开水的总体积不变,因此圆柱体露出水面的体积恰好等于石块的体积,
则石块的体积V石=V露=Sh露=0.05m2×0.02m=0.001m3;
则石块的密度: .
(1)确定压力的大小、方向和作用点,然后沿力的方向画一条带箭头的线段即可;
(2)①当圆柱体漂浮前,由于圆柱体占有一定体积,因此水面上升较快,压强增大较快。当圆柱体漂浮后,圆柱体不再占有下面水的体积,因此水面上上较慢,压强增大较慢。据此确定圆柱体漂浮时容器底部受到水的压强,再根据液体压强公式p=ρ液gh就计算容器中水的深度。
②当圆柱体刚刚漂浮时,圆柱体进入水中的深度等于此时水的深度,再与露出水的长度相加得到圆柱体的高度。根据浮沉条件,结合阿基米德原理,重力公式列出放出,进而计算出M的密度。
(3)当加入3kg水,圆柱体刚好漂浮,但是还未离开底部。根据计算出加水的体积,根据计算出圆柱体周围水的底面积。
当圆柱体漂浮后,容器底部增大的压力就等于增加水的重力,根据图片确定加水3kg和7kg时水对容器底部的压强,根据 计算出容器的底面积。
圆柱体的底面积等于容器的底面积减去周围水的底面积,接下来根据V=Sh计算出圆柱体的体积,根据G=mg=ρgV计算圆柱体的重力。
当圆柱体完全浸没时,根据阿基米德原理F浮=ρ液gV排计算出M和石块受到的总浮力,再根据二力平衡的条件G石块=F浮力-G计算石块的重力。
将石块用细线系在圆柱体下面时,它们仍然处于漂浮状态,则受到的浮力不变,那么排开水的总体积不变,因此圆柱体露出水面的体积恰好等于石块的体积,即V石=V露出。最后根据密度公式计算即可。
34.水平台面;CBA;30;130.4;偏小;③;;偏小
35.0.75;2;ACD;280Ω;180Ω;0.032W;0.192W
同课章节目录
