3.3.1轴对称和平移的坐标表示 教案
文档属性
| 名称 | 3.3.1轴对称和平移的坐标表示 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 10:41:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第4课时《3.3.1轴对称和平移的坐标表示 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 引导学生思考,作出点A关于x轴和y轴的对称点,并总结出坐标变化的规律. 让学生感知数学的乐趣,体验在平面直角坐标系中,做对称图形的过程.
学习者分析 在找关于坐标轴对称的点的坐标之间规检验其正确性的过程中,培养学生的语言表达能力,观察能力,归纳能力,养成良好的科学研究方法.
教学目标 能在平面直角坐标系中画出点关于坐标轴对称的点. 2.在找点,绘图的过程中是学生体验数形结合思想.
教学重点 用坐标表示点关于坐标轴对称的点的坐标.
教学难点 利用转化的思想,确定能代表轴对称图形的关键点.
学习活动设计
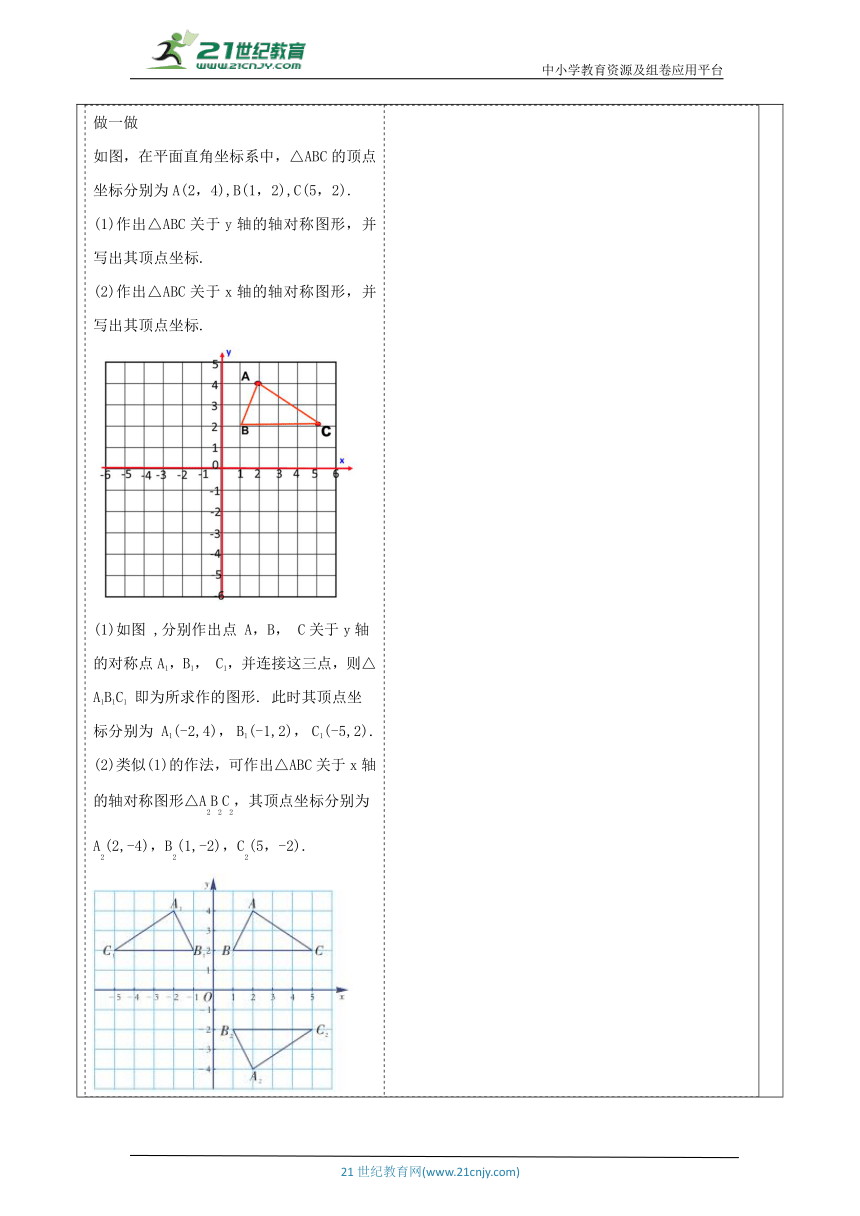
教师活动学生活动环节一:引入新课 已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:激发学生兴趣,引入新课主题,激发学生的兴趣,理解学生思考,让学生感知数学的乐趣,体验在平面直角坐标系中,做对称图形的过程. 环节二:新知探究教师活动2: 动脑筋 如图,在平面直角坐标系中,点A的坐标为(3,2). (1)分别作出点A关于x轴,y轴的对称点A′,A″,并写出它们的坐标; (2)比较:点A与A′的坐标之间有什么关系? 点A与A″呢? 总结规律: 坐标变化 改变A的坐标规律仍然成立吗? 一般地,在平面直角坐标系中,点(a, b)关于x轴对称的点的坐标为_______.点(a, b)关于y轴对称的点的坐标为_______.点(a,b)关于原点对称的点为(-a,-b) 做一做 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2). (1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标. (2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标. (1)如图 ,分别作出点 A,B, C关于y轴的对称点A1,B1, C1,并连接这三点,则△A1B1C1 即为所求作的图形. 此时其顶点坐标分别为 A1(-2,4), B1(-1,2), C1(-5,2). (2)类似(1)的作法,可作出△ABC关于x轴的轴对称图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2). 归纳 对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形。一找,二描,三连 学生活动2: 学生自学、互动。 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,引导学生分析题意,用坐标表示点关于坐标轴对称的点的坐标. 环节三:典例精析 例1、如图,求出折线OABCD各转折点的坐标以及它们关于y轴的对称点O′,A′,B′,C′,D′的坐标,并将点O′,A′,B′,C′,D′依次用线段连接起来. 总结:轴对称图形在直角坐标系中的画法 1、使对称轴与坐标轴重合 2、画出一侧的关键点,并求坐标 3、利用坐标关系,求另一侧关键点坐标 4、描点、连线 学生活动3: 参与教师分析和讲例题. 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,能在平面直角坐标系中画出点关于坐标轴对称的点。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为( ) A.(3,2) B.(2,-3) C.(-2,3) D.(-2,-3) 2.已知点P(-2,3)关于y轴的对称点为Q(a,b), 则a+b的值是( ) A.1 B.-1 C.5 D.-5 选做题: 3.如图,在方格纸上建立的平面直角坐标系中,Rt△ABC关于y轴对称的图形为Rt△DEF,则点A的对应点D的坐标是__________. 【综合拓展类作业】 4.在直角坐标系中,已知点A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称, (1)试确定点A、B的坐标; (2)如果点B关于x轴的对称的点是C,求△ABC
课堂总结
作业设计 【知识技能类作业】 必做题: 1.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( ) A.(-4,6) B.(4,6) C.(-2,1) D.(6,2) 选做题: 2、若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=__________. 【综合拓展类作业】 3.已知网格中最小正方形的边长为1。 (1)写出△ABC各点的坐标,做出△ABC关于y轴对称△A1B1C1 的图形,写出相应点的坐标。 (2)求△ABC的面积
教学反思
21世纪教育网(www.21cnjy.com)
分课时教学设计
第4课时《3.3.1轴对称和平移的坐标表示 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 引导学生思考,作出点A关于x轴和y轴的对称点,并总结出坐标变化的规律. 让学生感知数学的乐趣,体验在平面直角坐标系中,做对称图形的过程.
学习者分析 在找关于坐标轴对称的点的坐标之间规检验其正确性的过程中,培养学生的语言表达能力,观察能力,归纳能力,养成良好的科学研究方法.
教学目标 能在平面直角坐标系中画出点关于坐标轴对称的点. 2.在找点,绘图的过程中是学生体验数形结合思想.
教学重点 用坐标表示点关于坐标轴对称的点的坐标.
教学难点 利用转化的思想,确定能代表轴对称图形的关键点.
学习活动设计
教师活动学生活动环节一:引入新课 已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:激发学生兴趣,引入新课主题,激发学生的兴趣,理解学生思考,让学生感知数学的乐趣,体验在平面直角坐标系中,做对称图形的过程. 环节二:新知探究教师活动2: 动脑筋 如图,在平面直角坐标系中,点A的坐标为(3,2). (1)分别作出点A关于x轴,y轴的对称点A′,A″,并写出它们的坐标; (2)比较:点A与A′的坐标之间有什么关系? 点A与A″呢? 总结规律: 坐标变化 改变A的坐标规律仍然成立吗? 一般地,在平面直角坐标系中,点(a, b)关于x轴对称的点的坐标为_______.点(a, b)关于y轴对称的点的坐标为_______.点(a,b)关于原点对称的点为(-a,-b) 做一做 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2). (1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标. (2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标. (1)如图 ,分别作出点 A,B, C关于y轴的对称点A1,B1, C1,并连接这三点,则△A1B1C1 即为所求作的图形. 此时其顶点坐标分别为 A1(-2,4), B1(-1,2), C1(-5,2). (2)类似(1)的作法,可作出△ABC关于x轴的轴对称图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2). 归纳 对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形。一找,二描,三连 学生活动2: 学生自学、互动。 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,引导学生分析题意,用坐标表示点关于坐标轴对称的点的坐标. 环节三:典例精析 例1、如图,求出折线OABCD各转折点的坐标以及它们关于y轴的对称点O′,A′,B′,C′,D′的坐标,并将点O′,A′,B′,C′,D′依次用线段连接起来. 总结:轴对称图形在直角坐标系中的画法 1、使对称轴与坐标轴重合 2、画出一侧的关键点,并求坐标 3、利用坐标关系,求另一侧关键点坐标 4、描点、连线 学生活动3: 参与教师分析和讲例题. 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,能在平面直角坐标系中画出点关于坐标轴对称的点。
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为( ) A.(3,2) B.(2,-3) C.(-2,3) D.(-2,-3) 2.已知点P(-2,3)关于y轴的对称点为Q(a,b), 则a+b的值是( ) A.1 B.-1 C.5 D.-5 选做题: 3.如图,在方格纸上建立的平面直角坐标系中,Rt△ABC关于y轴对称的图形为Rt△DEF,则点A的对应点D的坐标是__________. 【综合拓展类作业】 4.在直角坐标系中,已知点A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称, (1)试确定点A、B的坐标; (2)如果点B关于x轴的对称的点是C,求△ABC
课堂总结
作业设计 【知识技能类作业】 必做题: 1.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( ) A.(-4,6) B.(4,6) C.(-2,1) D.(6,2) 选做题: 2、若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=__________. 【综合拓展类作业】 3.已知网格中最小正方形的边长为1。 (1)写出△ABC各点的坐标,做出△ABC关于y轴对称△A1B1C1 的图形,写出相应点的坐标。 (2)求△ABC的面积
教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
