2025年中考数学一轮复习 11 反比例函数 小测验(含解析)
文档属性
| 名称 | 2025年中考数学一轮复习 11 反比例函数 小测验(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 11:22:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11 反比例函数
分值:50分 时间30分钟
选择题(15分)
1、(2024·重庆·三模)下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
2、(2024·广东·模拟预测)对于反比例函数,下列说法正确的是( )
A.y随x的增大而增大 B.图象在第一、三象限
C.图象经过点 D.图象关于直线对称
3、(2024·广东·模拟预测)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:)是气体体积(单位:)的反比例函数,其图象如图所示.当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
4、(2024·河北·模拟预测)若k的取值范围在数轴上的表示如图所示,且,则反比例函数的图象不可能是( )
A. B.
C. D.
5、(2024·河北·模拟预测)如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,是反比例函数图像上的一个动点,连接,,当的面积为定值时,相应的点有且只有个,则点到直线的距离为( )
A. B. C. D.
填空题(15分)
6、(2024·重庆·模拟预测)若点,都在反比例函数的图象上,则 (填、或).
7、(2024·广东·模拟预测)物理课上老师讲到镜面成像时提到老花镜镜片的度数与焦距呈反比例函数的关系,引起了大家探究的兴趣.小明找了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小.此时他测量了镜片与光斑的距离,得到如下数据:
老花镜的度数 度
镜片与光斑的距离
根据以上数据,当老花镜的镜片与光斑的距离为时,老花镜的度数是 度.
8、(2024·陕西·模拟预测)已知P、Q两点分别在反比例函数和的图象上,若点与点关于y轴对称,则m的值为 .
9、(2024·安徽·三模)如图,直线与x轴交于点A,与y轴交于点B,与反比例函数的图象交于C,D两点,点M为线段的中点,轴交反比例函数图像于点N,P为x轴上任一点,若,则k的值为 .
10、(2024·湖南·模拟预测)如图,已知,,,…,是x轴上的点,且,分别过点,,,…,,作x轴的垂线交反比例函数()的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,…,的面积为,则等于 .
简答题(20分)
11、(2024·湖南·模拟预测)如图,反比例函数图象与正比例函数图象相交于点与点.
(1)试求反比例函数与正比例函数的函数表达式及点的坐标.
(2)请直接写出的解集.
12、(2024·吉林·二模)某气球内充满了一定质量的气体,当温度不变时,气球内的气压P(单位:)是气体体积V(单位:的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式.
(2)求当气球的体积是时,气球内的气压是多少千帕?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应不小于_____立方米.
13、(2024·广东·模拟预测)已知一次函数与反比例函数 的图象交于两点.
(1)①求一次函数和反比例函数的表达式;②求的面积.
在x轴的负半轴上,是否存在点P,使得为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
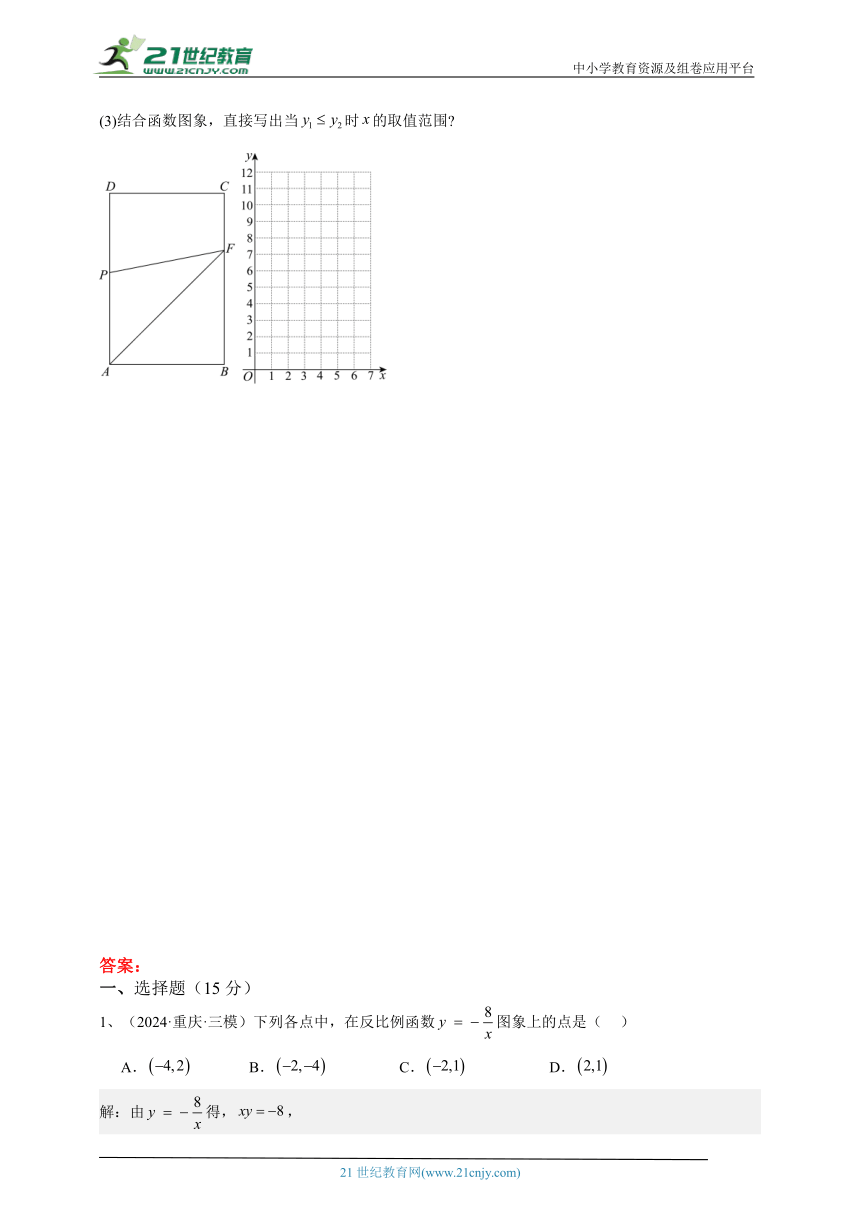
14、(2024·重庆·模拟预测)如图矩形中,,点为边上的三等分点(),动点从点出发,沿折线运动,到点停止运动.点的运动速度为每秒个单位长度,设点运动时间为秒,的面积为.
(1)请直接写出关于的函数解析式,并注明自变量的取值范围;
(2)若函数,请在平面直角坐标系中画出函数的图象,并写出函数的一条性质;
(3)结合函数图象,直接写出当时的取值范围
答案:
一、选择题(15分)
1、(2024·重庆·三模)下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
解:由得,,
、∵,
∴点在反比例函数图象上,该选项符合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
故选:.
2、(2024·广东·模拟预测)对于反比例函数,下列说法正确的是( )
A.y随x的增大而增大 B.图象在第一、三象限
C.图象经过点 D.图象关于直线对称
解:对于反比例函数,∵.
∴该函数的图象在第二、四象限,在每个象限内,y随x的增大而增大,故选项A,B错误;把代入中,得,
∴图象不经过点,故选项C错误.
反比例函数的图象关于直线对称,故选项D正确.
故选D.
3、(2024·广东·模拟预测)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:)是气体体积(单位:)的反比例函数,其图象如图所示.当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
解:设该反比例函数的解析式为,
把代入得:,
解得:,
∴该反比例函数的解析式为,
把代入得:,
解得:,
∵,
∴在第一象限内,p随V的增大而减小,
∴为了安全起见,气球的体积应不小于,
故选:B.
4、(2024·河北·模拟预测)若k的取值范围在数轴上的表示如图所示,且,则反比例函数的图象不可能是( )
A. B.
C. D.
解:由数轴可得,
A.过,则,符合题意;
B.过,则,不符合题意;
C.过,则,不符合题意;
D.过,则,不符合题意;
故选:A.
5、(2024·河北·模拟预测)如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,是反比例函数图像上的一个动点,连接,,当的面积为定值时,相应的点有且只有个,则点到直线的距离为( )
A. B. C. D.
解:如图,过点作于点,
当的面积为定值时,相应的点有且只有个,
此时点到的距离是点在下方反比例函数图像上点到的最大距离,即点位于点或或处(点,,到直线的距离相等),
由图可知,当为的中点时,即为所求,
联立:,
解得:或,
,,
此时,
将直线向左平移个单位,得到直线,使得该直线与反比例函数图像只有一个交点,
直线的解析式为,
与反比例函数联立可得:,
整理得:,
反比例函数与直线只有一个交点,
,
解得:或(不合题意,舍去),
,
解得:,
,
,
故选:B.
二、填空题(15分)
6、(2024·重庆·模拟预测)若点,都在反比例函数的图象上,则 (填、或).
解:反比例函数中,
该函数图象经过二、四象限,且在二、四象限中均有随着的增大而增大,
,,
.
故答案为:.
7、(2024·广东·模拟预测)物理课上老师讲到镜面成像时提到老花镜镜片的度数与焦距呈反比例函数的关系,引起了大家探究的兴趣.小明找了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小.此时他测量了镜片与光斑的距离,得到如下数据:
老花镜的度数 度
镜片与光斑的距离
根据以上数据,当老花镜的镜片与光斑的距离为时,老花镜的度数是 度.
解:由题意可知:D与f成反比例函数,设,把代入得,,
∴,
∴,
当时,,
故答案为:.
8、(2024·陕西·模拟预测)已知P、Q两点分别在反比例函数和的图象上,若点与点关于y轴对称,则m的值为 .
解:设,
点与点关于y轴对称,
点,
P、Q两点分别在反比例函数和的图象上,
解得:,
故答案为∶1.
9、(2024·安徽·三模)如图,直线与x轴交于点A,与y轴交于点B,与反比例函数的图象交于C,D两点,点M为线段的中点,轴交反比例函数图像于点N,P为x轴上任一点,若,则k的值为 .
解:∵直线与x轴交于点A,与y轴交于点B,
∴,,
∵点M为线段的中点,
∴,
∵轴交反比例函数图像于点N,
∴,
∵,
∴,
解得:,
故答案为:
10、(2024·湖南·模拟预测)如图,已知,,,…,是x轴上的点,且,分别过点,,,…,,作x轴的垂线交反比例函数()的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,…,的面积为,则等于 .
解:∵,
∴设,,,…,,
∵,,,…,在反比例函数的图象上,
∴,,,…,,
∴;
∴;
;
;
…
;
∴.
∴.
故答案为:.
三、简答题(20分)
11、(2024·湖南·模拟预测)如图,反比例函数图象与正比例函数图象相交于点与点.
(1)试求反比例函数与正比例函数的函数表达式及点的坐标.
(2)请直接写出的解集.
(1)解:反比例函数图象与正比例函数图象相交于点,
,即反比例函数表达式为;
,即正比例函数表达式为;
反比例函数图象与正比例函数图象相交于点与点,
联立,解得或,即;
(2)解:的解集是指反比例函数图象在正比例函数图象上方部分对应的自变量的取值范围,如图所示:
、,
当或时,反比例函数图象在正比例函数图象上方,即的解集是或
12、(2024·吉林·二模)某气球内充满了一定质量的气体,当温度不变时,气球内的气压P(单位:)是气体体积V(单位:的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式.
(2)求当气球的体积是时,气球内的气压是多少千帕?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应不小于_____立方米.
(1)解:设反比例函数的解析式,根据图象得在该函数图象上,
,
解得:,
反比例函数的解析式;
(2)把代入,
得(千帕),
∴当气球的体积是时,气球内的气压是120千帕;
(3)由题意知,,
解得,
∴为了安全起见,气球的体积应不小于立方米.
故答案为:.
13、(2024·广东·模拟预测)已知一次函数与反比例函数 的图象交于两点.
(1)①求一次函数和反比例函数的表达式;②求的面积.
在x轴的负半轴上,是否存在点P,使得为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)解:①将代入 得: ,
解得:;
∴反比例函数的表达式为: ;
∴,即:;
将、代入得:,
解得:,
∴一次函数的表达式为:
②设一次函数与轴交于点,如图所示:
由得;
∴
∴
(2)解:设点,
,则,
解得:;
,则,
解得:或(舍);
,则,
解得:;
综上所述:点P的坐标为或或
14、(2024·重庆·模拟预测)如图矩形中,,点为边上的三等分点(),动点从点出发,沿折线运动,到点停止运动.点的运动速度为每秒个单位长度,设点运动时间为秒,的面积为.
(1)请直接写出关于的函数解析式,并注明自变量的取值范围;
(2)若函数,请在平面直角坐标系中画出函数的图象,并写出函数的一条性质;
(3)结合函数图象,直接写出当时的取值范围
(1)解:在矩形中,,,
∵点为边上的三等分点(),
∴,,
分两种情况:①当时,即点P在边上,则
;
②当时,即点P在边上,则
∴
;
综上,关于的函数解析式为:;
(2)解:用描点法作出函数图象即可,
当时,随着x的增大而增大;当时,随着x的增大而减小(答案不唯一)
(3)解:由图象可得,当时的取值范围为或;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11 反比例函数
分值:50分 时间30分钟
选择题(15分)
1、(2024·重庆·三模)下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
2、(2024·广东·模拟预测)对于反比例函数,下列说法正确的是( )
A.y随x的增大而增大 B.图象在第一、三象限
C.图象经过点 D.图象关于直线对称
3、(2024·广东·模拟预测)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:)是气体体积(单位:)的反比例函数,其图象如图所示.当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
4、(2024·河北·模拟预测)若k的取值范围在数轴上的表示如图所示,且,则反比例函数的图象不可能是( )
A. B.
C. D.
5、(2024·河北·模拟预测)如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,是反比例函数图像上的一个动点,连接,,当的面积为定值时,相应的点有且只有个,则点到直线的距离为( )
A. B. C. D.
填空题(15分)
6、(2024·重庆·模拟预测)若点,都在反比例函数的图象上,则 (填、或).
7、(2024·广东·模拟预测)物理课上老师讲到镜面成像时提到老花镜镜片的度数与焦距呈反比例函数的关系,引起了大家探究的兴趣.小明找了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小.此时他测量了镜片与光斑的距离,得到如下数据:
老花镜的度数 度
镜片与光斑的距离
根据以上数据,当老花镜的镜片与光斑的距离为时,老花镜的度数是 度.
8、(2024·陕西·模拟预测)已知P、Q两点分别在反比例函数和的图象上,若点与点关于y轴对称,则m的值为 .
9、(2024·安徽·三模)如图,直线与x轴交于点A,与y轴交于点B,与反比例函数的图象交于C,D两点,点M为线段的中点,轴交反比例函数图像于点N,P为x轴上任一点,若,则k的值为 .
10、(2024·湖南·模拟预测)如图,已知,,,…,是x轴上的点,且,分别过点,,,…,,作x轴的垂线交反比例函数()的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,…,的面积为,则等于 .
简答题(20分)
11、(2024·湖南·模拟预测)如图,反比例函数图象与正比例函数图象相交于点与点.
(1)试求反比例函数与正比例函数的函数表达式及点的坐标.
(2)请直接写出的解集.
12、(2024·吉林·二模)某气球内充满了一定质量的气体,当温度不变时,气球内的气压P(单位:)是气体体积V(单位:的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式.
(2)求当气球的体积是时,气球内的气压是多少千帕?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应不小于_____立方米.
13、(2024·广东·模拟预测)已知一次函数与反比例函数 的图象交于两点.
(1)①求一次函数和反比例函数的表达式;②求的面积.
在x轴的负半轴上,是否存在点P,使得为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
14、(2024·重庆·模拟预测)如图矩形中,,点为边上的三等分点(),动点从点出发,沿折线运动,到点停止运动.点的运动速度为每秒个单位长度,设点运动时间为秒,的面积为.
(1)请直接写出关于的函数解析式,并注明自变量的取值范围;
(2)若函数,请在平面直角坐标系中画出函数的图象,并写出函数的一条性质;
(3)结合函数图象,直接写出当时的取值范围
答案:
一、选择题(15分)
1、(2024·重庆·三模)下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
解:由得,,
、∵,
∴点在反比例函数图象上,该选项符合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
、∵,
∴点不在反比例函数图象上,该选项不合题意;
故选:.
2、(2024·广东·模拟预测)对于反比例函数,下列说法正确的是( )
A.y随x的增大而增大 B.图象在第一、三象限
C.图象经过点 D.图象关于直线对称
解:对于反比例函数,∵.
∴该函数的图象在第二、四象限,在每个象限内,y随x的增大而增大,故选项A,B错误;把代入中,得,
∴图象不经过点,故选项C错误.
反比例函数的图象关于直线对称,故选项D正确.
故选D.
3、(2024·广东·模拟预测)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:)是气体体积(单位:)的反比例函数,其图象如图所示.当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
解:设该反比例函数的解析式为,
把代入得:,
解得:,
∴该反比例函数的解析式为,
把代入得:,
解得:,
∵,
∴在第一象限内,p随V的增大而减小,
∴为了安全起见,气球的体积应不小于,
故选:B.
4、(2024·河北·模拟预测)若k的取值范围在数轴上的表示如图所示,且,则反比例函数的图象不可能是( )
A. B.
C. D.
解:由数轴可得,
A.过,则,符合题意;
B.过,则,不符合题意;
C.过,则,不符合题意;
D.过,则,不符合题意;
故选:A.
5、(2024·河北·模拟预测)如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像交于,两点,是反比例函数图像上的一个动点,连接,,当的面积为定值时,相应的点有且只有个,则点到直线的距离为( )
A. B. C. D.
解:如图,过点作于点,
当的面积为定值时,相应的点有且只有个,
此时点到的距离是点在下方反比例函数图像上点到的最大距离,即点位于点或或处(点,,到直线的距离相等),
由图可知,当为的中点时,即为所求,
联立:,
解得:或,
,,
此时,
将直线向左平移个单位,得到直线,使得该直线与反比例函数图像只有一个交点,
直线的解析式为,
与反比例函数联立可得:,
整理得:,
反比例函数与直线只有一个交点,
,
解得:或(不合题意,舍去),
,
解得:,
,
,
故选:B.
二、填空题(15分)
6、(2024·重庆·模拟预测)若点,都在反比例函数的图象上,则 (填、或).
解:反比例函数中,
该函数图象经过二、四象限,且在二、四象限中均有随着的增大而增大,
,,
.
故答案为:.
7、(2024·广东·模拟预测)物理课上老师讲到镜面成像时提到老花镜镜片的度数与焦距呈反比例函数的关系,引起了大家探究的兴趣.小明找了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小.此时他测量了镜片与光斑的距离,得到如下数据:
老花镜的度数 度
镜片与光斑的距离
根据以上数据,当老花镜的镜片与光斑的距离为时,老花镜的度数是 度.
解:由题意可知:D与f成反比例函数,设,把代入得,,
∴,
∴,
当时,,
故答案为:.
8、(2024·陕西·模拟预测)已知P、Q两点分别在反比例函数和的图象上,若点与点关于y轴对称,则m的值为 .
解:设,
点与点关于y轴对称,
点,
P、Q两点分别在反比例函数和的图象上,
解得:,
故答案为∶1.
9、(2024·安徽·三模)如图,直线与x轴交于点A,与y轴交于点B,与反比例函数的图象交于C,D两点,点M为线段的中点,轴交反比例函数图像于点N,P为x轴上任一点,若,则k的值为 .
解:∵直线与x轴交于点A,与y轴交于点B,
∴,,
∵点M为线段的中点,
∴,
∵轴交反比例函数图像于点N,
∴,
∵,
∴,
解得:,
故答案为:
10、(2024·湖南·模拟预测)如图,已知,,,…,是x轴上的点,且,分别过点,,,…,,作x轴的垂线交反比例函数()的图象于点,,,…,,过点作于点,过点作于点,…,记的面积为,的面积为,…,的面积为,则等于 .
解:∵,
∴设,,,…,,
∵,,,…,在反比例函数的图象上,
∴,,,…,,
∴;
∴;
;
;
…
;
∴.
∴.
故答案为:.
三、简答题(20分)
11、(2024·湖南·模拟预测)如图,反比例函数图象与正比例函数图象相交于点与点.
(1)试求反比例函数与正比例函数的函数表达式及点的坐标.
(2)请直接写出的解集.
(1)解:反比例函数图象与正比例函数图象相交于点,
,即反比例函数表达式为;
,即正比例函数表达式为;
反比例函数图象与正比例函数图象相交于点与点,
联立,解得或,即;
(2)解:的解集是指反比例函数图象在正比例函数图象上方部分对应的自变量的取值范围,如图所示:
、,
当或时,反比例函数图象在正比例函数图象上方,即的解集是或
12、(2024·吉林·二模)某气球内充满了一定质量的气体,当温度不变时,气球内的气压P(单位:)是气体体积V(单位:的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式.
(2)求当气球的体积是时,气球内的气压是多少千帕?
(3)当气球内的气压大于时,气球将爆炸,为了安全起见,气球的体积应不小于_____立方米.
(1)解:设反比例函数的解析式,根据图象得在该函数图象上,
,
解得:,
反比例函数的解析式;
(2)把代入,
得(千帕),
∴当气球的体积是时,气球内的气压是120千帕;
(3)由题意知,,
解得,
∴为了安全起见,气球的体积应不小于立方米.
故答案为:.
13、(2024·广东·模拟预测)已知一次函数与反比例函数 的图象交于两点.
(1)①求一次函数和反比例函数的表达式;②求的面积.
在x轴的负半轴上,是否存在点P,使得为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)解:①将代入 得: ,
解得:;
∴反比例函数的表达式为: ;
∴,即:;
将、代入得:,
解得:,
∴一次函数的表达式为:
②设一次函数与轴交于点,如图所示:
由得;
∴
∴
(2)解:设点,
,则,
解得:;
,则,
解得:或(舍);
,则,
解得:;
综上所述:点P的坐标为或或
14、(2024·重庆·模拟预测)如图矩形中,,点为边上的三等分点(),动点从点出发,沿折线运动,到点停止运动.点的运动速度为每秒个单位长度,设点运动时间为秒,的面积为.
(1)请直接写出关于的函数解析式,并注明自变量的取值范围;
(2)若函数,请在平面直角坐标系中画出函数的图象,并写出函数的一条性质;
(3)结合函数图象,直接写出当时的取值范围
(1)解:在矩形中,,,
∵点为边上的三等分点(),
∴,,
分两种情况:①当时,即点P在边上,则
;
②当时,即点P在边上,则
∴
;
综上,关于的函数解析式为:;
(2)解:用描点法作出函数图象即可,
当时,随着x的增大而增大;当时,随着x的增大而减小(答案不唯一)
(3)解:由图象可得,当时的取值范围为或;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
