11.2.3一元一次不等式的应用 课件(共21张PPT) 2024-2025人教版七年级数学下册
文档属性
| 名称 | 11.2.3一元一次不等式的应用 课件(共21张PPT) 2024-2025人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 18:19:00 | ||
图片预览




文档简介
(共21张PPT)
11.2.3一元一次不等式的应用
第十一章 不等式与不等式组
2024人教版数学七年级下册【精做课件】
展示一些生活中的实际问题情境,如:
某电影院规定,身高 1.2 米以下(含 1.2 米)的儿童可免费观影,设儿童身高为 h 米,如何用数学式子表示 h 的取值范围?
一辆轿车在某公路上的行驶速度不得超过 80 千米 / 小时,设轿车的速度为 v 千米 / 小时,怎样用式子表示 v 的限制条件?
引导学生分析这些问题中数量之间的关系,引出不等式的概念,从而导入本节课的主题 —— 不等式与不等式组。
(二)知识讲解(20 分钟)
不等式的相关概念
通过上述实际问题中的式子,如 h≤1.2,v≤80 等,明确不等式的定义:用不等号(>,<,≥,≤,≠)表示不等关系的式子叫做不等式。
给出一些具体的不等式,让学生判断哪些是不等式,加深对不等式概念的理解。
讲解不等式的解的概念:使不等式成立的未知数的值叫做不等式的解。例如,在不等式 x>3 中,4,5,3.5 等都是它的解。
进一步引出不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。如不等式 x>3 的解集是所有大于 3 的数,并用数轴表示解集的方法,直观展示解集的范围。
不等式的性质
通过一些具体的不等式,如 2<3,让学生在不等式两边同时加上或减去同一个数,观察不等号方向的变化情况,归纳出不等式的性质 1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。即如果 a>b,那么 a±c>b±c。
类似地,让学生在不等式两边同时乘以或除以同一个正数,探究不等号方向的变化,得出不等式的性质 2:不等式两边乘(或除以)同一个正数,不等号的方向不变。即如果 a>b,c>0,那么 ac>bc(或 a/c>b/c)。
重点讲解不等式性质 3,通过实例,如 2<3,两边同时乘以 -1,得到 -2> -3,让学生观察不等号方向改变的情况,总结出不等式性质 3:不等式两边乘(或除以)同一个负数,不等号的方向改变。即如果 a>b,c<0,那么 ac<bc(或 a/c<b/c)。
通过一些简单的练习,让学生运用不等式的性质对不等式进行变形,巩固对性质的理解和掌握。
一元一次不等式的解法
给出一元一次不等式的定义:只含有一个未知数,并且未知数的次数是 1,系数不为 0,左右两边为整式的不等式叫做一元一次不等式。例如,3x - 5>7 就是一元一次不等式。
以解不等式 3x - 5>7 为例,详细讲解一元一次不等式的解法步骤:
移项:将常数项 -5 移到不等式右边,得到 3x>7 + 5。
合并同类项:计算右边式子,3x>12。
系数化为 1:根据不等式性质 2,两边同时除以 3,得到 x>4。
强调在系数化为 1 时,如果系数是负数,要根据不等式性质 3 改变不等号方向。然后让学生做几道类似的练习题,教师巡视指导,纠正学生在解题过程中出现的错误。
(三)案例分析(15 分钟)
展示案例:某商店以每辆 250 元的进价购入 200 辆自行车,并以每辆 275 元的价格销售,两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
引导学生分析题目中的数量关系,设已售出 x 辆自行车,根据 “销售款超过进货款” 这一不等关系列出不等式:275x>250×200。
让学生分组讨论如何解这个不等式,并求出 x 的取值范围。
各小组汇报讨论结果,教师进行点评和总结,强调列不等式解应用题的关键是找出题目中的不等关系,同时注意根据实际情况对解进行合理的取舍。
(四)课堂练习(10 分钟)
给出练习题:
解不等式 2x + 3< - 1,并在数轴上表示解集。
解不等式组:\(\begin{cases}2x - 1>x + 1 \\ x + 8<4x - 1\end{cases}\)
学生独立完成练习,教师巡视指导,对学生的解题过程进行观察和分析,及时发现学生存在的问题,如移项变号错误、不等式性质应用错误、解不等式组时确定解集错误等,并进行个别辅导。对于学生普遍存在的问题,在练习结束后进行集中讲解和纠正。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学的主要内容,包括不等式的概念、性质,一元一次不等式的解法以及一元一次不等式组的初步认识。重点强调不等式性质 3 的应用以及解不等式和不等式组的步骤和注意事项。
引导学生总结在解决实际问题中如何建立不等式模型,以及用数学知识解决实际问题的一般思路和方法。鼓励学生在今后的学习和生活中,善于发现和提出与不等式相关的问题,并尝试用所学知识去解决。
(六)作业布置(5 分钟)
教材课后相关练习题,包括不等式的概念辨析、性质应用、解不等式及不等式组等题目,通过作业进一步巩固学生本节课所学的知识和技能。
布置一道实际应用作业:让学生调查自己所在班级同学的零花钱使用情况,设定一个合理的零花钱标准,然后根据调查数据列出不等式,分析班级中零花钱使用符合标准的同学人数占总人数的比例等问题,并撰写一份简单的调查报告。这样的作业既可以让学生巩固不等式知识,又能提高学生运用数学知识解决实际问题的能力和社会实践能力。
五、教学反思
在本节课的教学过程中,通过实际问题情境引入,学生对不等式的概念和应用有了较好的理解。在讲解不等式性质和解法时,学生通过自主探究和练习,基本掌握了相关知识和技能。但在不等式性质 3 的应用以及解不等式组确定解集时,部分学生仍容易出错。在今后的教学中,要加强这方面的针对性练习,通过更多的实例和不同类型的题目,帮助学生加深对不等式性质的理解和掌握,提高学生解不等式及不等式组的准确性和熟练程度。同时,要更加关注学生在解决实际问题时的思维过程,培养学生分析问题和解决问题的能力,提高学生的数学应用意识。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
进一步学习通过列一元一次不等式解决生活中的实际问题,体会分类讨论思想在用不等式解决实际问题中的应用.
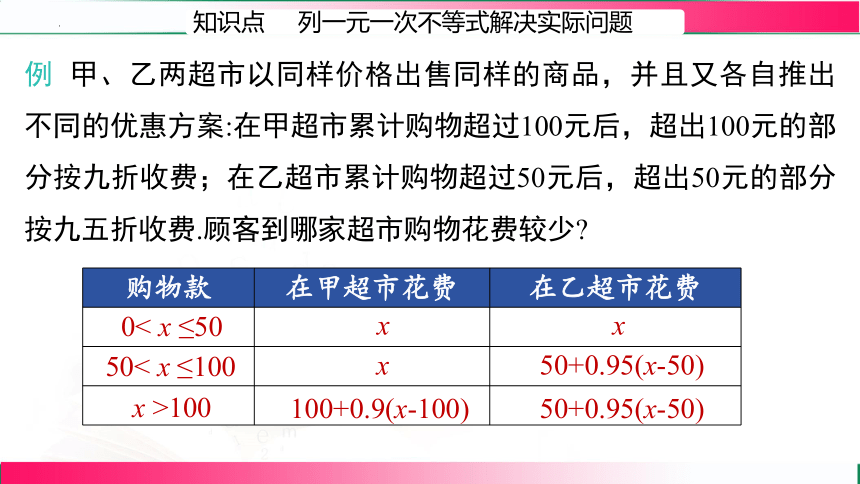
例 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
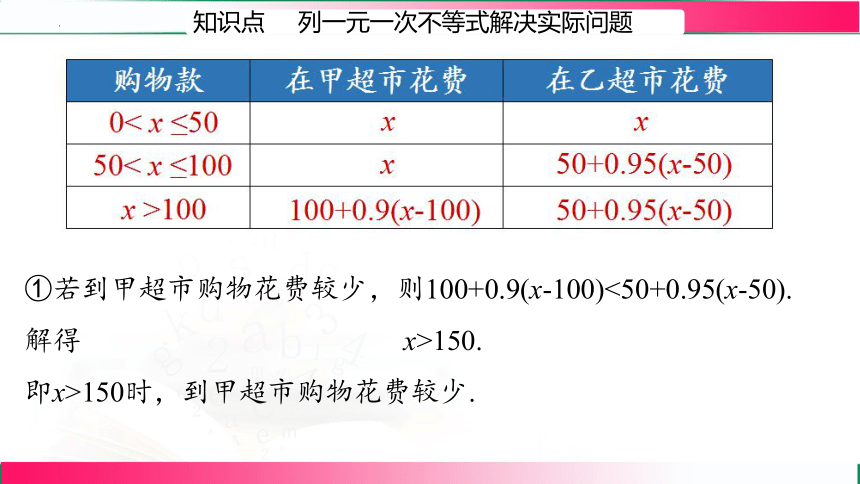
知识点 列一元一次不等式解决实际问题
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠,因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
例 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
知识点 列一元一次不等式解决实际问题
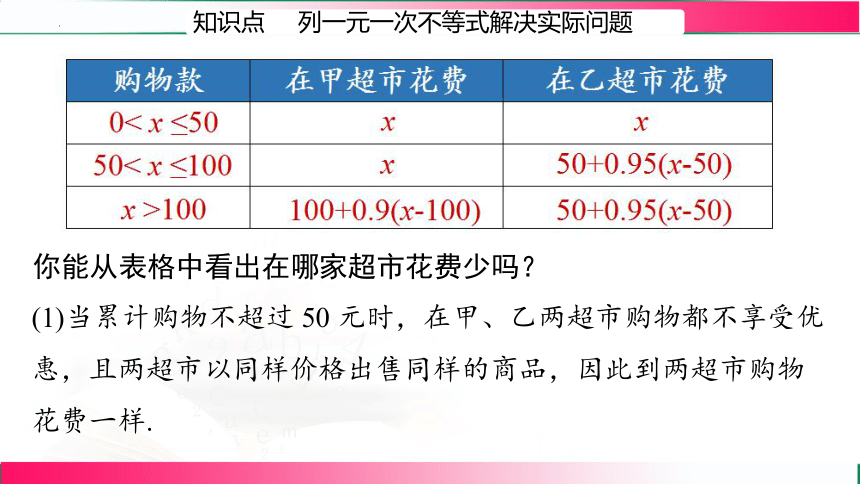
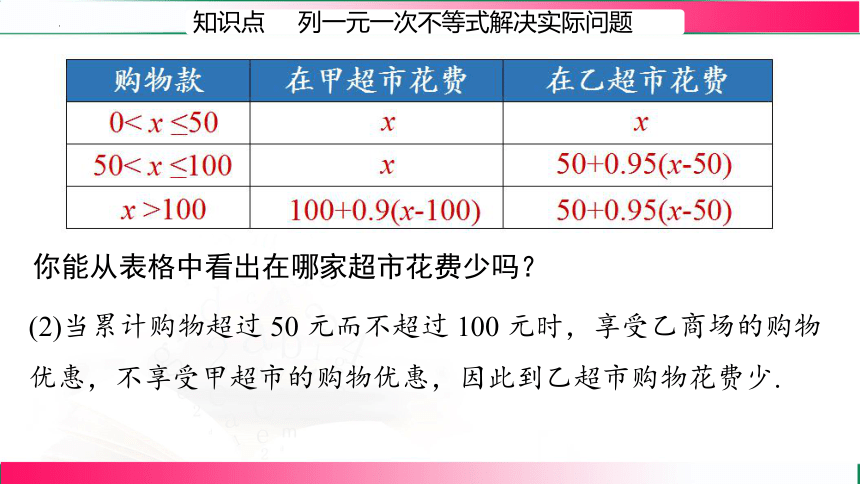
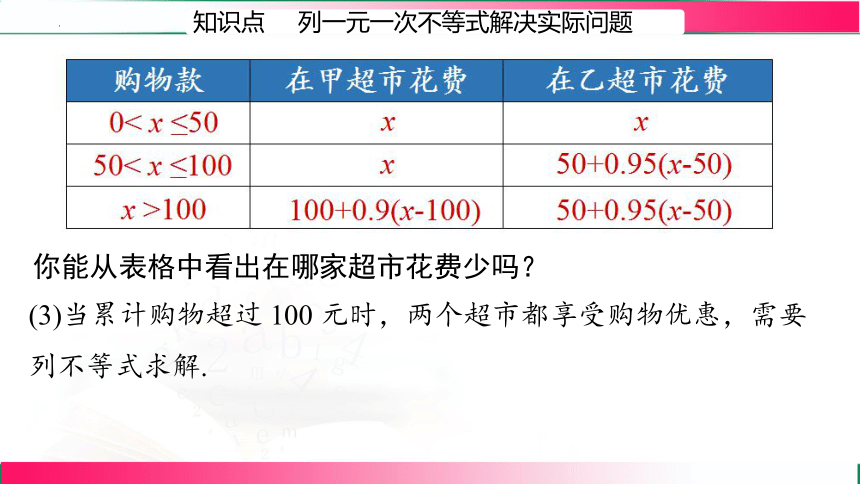
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(1)当累计购物不超过 50 元时,在甲、乙两超市购物都不享受优惠,且两超市以同样价格出售同样的商品,因此到两超市购物花费一样.
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(2)当累计购物超过 50 元而不超过 100 元时,享受乙商场的购物优惠,不享受甲超市的购物优惠,因此到乙超市购物花费少.
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
①若到甲超市购物花费较少,则100+0.9(x-100)<50+0.95(x-50).
解得 x>150.
即x>150时,到甲超市购物花费较少.
知识点 列一元一次不等式解决实际问题
②若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).
解得 x<150.
即100知识点 列一元一次不等式解决实际问题
③若到两超市购物花费相同,则
100+0.9(x-100)=50+0.95(x-50).
解得 x=150.
即x=150时,到甲、乙两超市购物花费相同.
知识点 列一元一次不等式解决实际问题
1. 某超市花费750元购进草莓100千克,销售中有 的正常
损耗,为避免亏本(其他费用不考虑),售价至少定为每千
克多少元?设售价定为每千克 元,根据题意所列不等式正
确的是( )
A
A. B.
C. D.
2. 某人贷款2.2万元购进一台机器,生产某种产品.已知产品
的成本是每个5元,售价是每个8元,应付的税款和其他费用
是售价的 ,若每个月能生产、销售2 000个产品,问至
少几个月后能赚回这台机器的贷款?( )
B
A. 4 B. 5 C. 6 D. 7
【点拨】应付的税款和其他费用为
(元),每个月利润为
(元),
设 个月后能赚回这台机器的贷款,
则 ,
解得 .
所以至少5个月后能赚回这台机器的贷款.故选B.
3. [2024武汉江汉区三模] 从地向 地打长途电话,通话时
间不超过收费2.4元,超过 后每分钟加收1元.本题
中通话时间取整数,不足的通话时间按 计费.若小
江有10元钱,则他打一次电话最多可以通话的时间是( )
B
A. B. C. D.
【点拨】设他打一次电话可以通话的时间是 ,
根据题意得 ,
解得 .
为正整数, 的最大值为10.故选B.
4. [2024聊城东昌府区期末] 某市的出租车收费标准是:起步
价为6元(即行驶距离不超过3千米应付车费6元),超过3千
米后,每增加1千米加收1.4元(不足1千米按1千米收费).人
从甲地到乙地经过的路程是千米,出租车费为17.2元,则
为 ( )
B
A. 11 B.
C. 10 D.
【点拨】根据题意,得 ,
.故选B.
5. 黄河流域两岸地带培育的大红枣,学名“木
枣”,自古以来就被列为“五果”(桃、李、栗、杏、枣)之一.
某超市购进一批大红枣,一箱的进价为18元,标价为21元,
在春节期间,该超市准备打折销售,但要保证利润率不低于
,则至多可以打____折.
九
【点拨】设打折销售,由题意可得 ,
解得 ,
至多打九折.
6.[2024山西] 为加强校园消防安全,学校计划购买某种型号
的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为
540元/个,干粉灭火器的单价为380元/个.若学校购买这两种
灭火器的总价不超过21 000元,则最多可购买这种型号的水
基灭火器多少个?
【解】设可购买这种型号的水基灭火器 个,则购买干粉灭
火器 个,
根据题意得 ,
解得 .
为整数, 的最大值为12.
答:最多可购买这种型号的水基灭火器12个.
检验
设未知数
列不等式
数学问题
(一元一次不等式)
实际问题
(包含不等关系)
数学问题的解
(不等式的解集)
实际问题的答案
解不等式
11.2.3一元一次不等式的应用
第十一章 不等式与不等式组
2024人教版数学七年级下册【精做课件】
展示一些生活中的实际问题情境,如:
某电影院规定,身高 1.2 米以下(含 1.2 米)的儿童可免费观影,设儿童身高为 h 米,如何用数学式子表示 h 的取值范围?
一辆轿车在某公路上的行驶速度不得超过 80 千米 / 小时,设轿车的速度为 v 千米 / 小时,怎样用式子表示 v 的限制条件?
引导学生分析这些问题中数量之间的关系,引出不等式的概念,从而导入本节课的主题 —— 不等式与不等式组。
(二)知识讲解(20 分钟)
不等式的相关概念
通过上述实际问题中的式子,如 h≤1.2,v≤80 等,明确不等式的定义:用不等号(>,<,≥,≤,≠)表示不等关系的式子叫做不等式。
给出一些具体的不等式,让学生判断哪些是不等式,加深对不等式概念的理解。
讲解不等式的解的概念:使不等式成立的未知数的值叫做不等式的解。例如,在不等式 x>3 中,4,5,3.5 等都是它的解。
进一步引出不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。如不等式 x>3 的解集是所有大于 3 的数,并用数轴表示解集的方法,直观展示解集的范围。
不等式的性质
通过一些具体的不等式,如 2<3,让学生在不等式两边同时加上或减去同一个数,观察不等号方向的变化情况,归纳出不等式的性质 1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。即如果 a>b,那么 a±c>b±c。
类似地,让学生在不等式两边同时乘以或除以同一个正数,探究不等号方向的变化,得出不等式的性质 2:不等式两边乘(或除以)同一个正数,不等号的方向不变。即如果 a>b,c>0,那么 ac>bc(或 a/c>b/c)。
重点讲解不等式性质 3,通过实例,如 2<3,两边同时乘以 -1,得到 -2> -3,让学生观察不等号方向改变的情况,总结出不等式性质 3:不等式两边乘(或除以)同一个负数,不等号的方向改变。即如果 a>b,c<0,那么 ac<bc(或 a/c<b/c)。
通过一些简单的练习,让学生运用不等式的性质对不等式进行变形,巩固对性质的理解和掌握。
一元一次不等式的解法
给出一元一次不等式的定义:只含有一个未知数,并且未知数的次数是 1,系数不为 0,左右两边为整式的不等式叫做一元一次不等式。例如,3x - 5>7 就是一元一次不等式。
以解不等式 3x - 5>7 为例,详细讲解一元一次不等式的解法步骤:
移项:将常数项 -5 移到不等式右边,得到 3x>7 + 5。
合并同类项:计算右边式子,3x>12。
系数化为 1:根据不等式性质 2,两边同时除以 3,得到 x>4。
强调在系数化为 1 时,如果系数是负数,要根据不等式性质 3 改变不等号方向。然后让学生做几道类似的练习题,教师巡视指导,纠正学生在解题过程中出现的错误。
(三)案例分析(15 分钟)
展示案例:某商店以每辆 250 元的进价购入 200 辆自行车,并以每辆 275 元的价格销售,两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
引导学生分析题目中的数量关系,设已售出 x 辆自行车,根据 “销售款超过进货款” 这一不等关系列出不等式:275x>250×200。
让学生分组讨论如何解这个不等式,并求出 x 的取值范围。
各小组汇报讨论结果,教师进行点评和总结,强调列不等式解应用题的关键是找出题目中的不等关系,同时注意根据实际情况对解进行合理的取舍。
(四)课堂练习(10 分钟)
给出练习题:
解不等式 2x + 3< - 1,并在数轴上表示解集。
解不等式组:\(\begin{cases}2x - 1>x + 1 \\ x + 8<4x - 1\end{cases}\)
学生独立完成练习,教师巡视指导,对学生的解题过程进行观察和分析,及时发现学生存在的问题,如移项变号错误、不等式性质应用错误、解不等式组时确定解集错误等,并进行个别辅导。对于学生普遍存在的问题,在练习结束后进行集中讲解和纠正。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学的主要内容,包括不等式的概念、性质,一元一次不等式的解法以及一元一次不等式组的初步认识。重点强调不等式性质 3 的应用以及解不等式和不等式组的步骤和注意事项。
引导学生总结在解决实际问题中如何建立不等式模型,以及用数学知识解决实际问题的一般思路和方法。鼓励学生在今后的学习和生活中,善于发现和提出与不等式相关的问题,并尝试用所学知识去解决。
(六)作业布置(5 分钟)
教材课后相关练习题,包括不等式的概念辨析、性质应用、解不等式及不等式组等题目,通过作业进一步巩固学生本节课所学的知识和技能。
布置一道实际应用作业:让学生调查自己所在班级同学的零花钱使用情况,设定一个合理的零花钱标准,然后根据调查数据列出不等式,分析班级中零花钱使用符合标准的同学人数占总人数的比例等问题,并撰写一份简单的调查报告。这样的作业既可以让学生巩固不等式知识,又能提高学生运用数学知识解决实际问题的能力和社会实践能力。
五、教学反思
在本节课的教学过程中,通过实际问题情境引入,学生对不等式的概念和应用有了较好的理解。在讲解不等式性质和解法时,学生通过自主探究和练习,基本掌握了相关知识和技能。但在不等式性质 3 的应用以及解不等式组确定解集时,部分学生仍容易出错。在今后的教学中,要加强这方面的针对性练习,通过更多的实例和不同类型的题目,帮助学生加深对不等式性质的理解和掌握,提高学生解不等式及不等式组的准确性和熟练程度。同时,要更加关注学生在解决实际问题时的思维过程,培养学生分析问题和解决问题的能力,提高学生的数学应用意识。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
进一步学习通过列一元一次不等式解决生活中的实际问题,体会分类讨论思想在用不等式解决实际问题中的应用.
例 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
知识点 列一元一次不等式解决实际问题
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠,因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
例 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
知识点 列一元一次不等式解决实际问题
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(1)当累计购物不超过 50 元时,在甲、乙两超市购物都不享受优惠,且两超市以同样价格出售同样的商品,因此到两超市购物花费一样.
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(2)当累计购物超过 50 元而不超过 100 元时,享受乙商场的购物优惠,不享受甲超市的购物优惠,因此到乙超市购物花费少.
知识点 列一元一次不等式解决实际问题
你能从表格中看出在哪家超市花费少吗?
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
①若到甲超市购物花费较少,则100+0.9(x-100)<50+0.95(x-50).
解得 x>150.
即x>150时,到甲超市购物花费较少.
知识点 列一元一次不等式解决实际问题
②若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).
解得 x<150.
即100
③若到两超市购物花费相同,则
100+0.9(x-100)=50+0.95(x-50).
解得 x=150.
即x=150时,到甲、乙两超市购物花费相同.
知识点 列一元一次不等式解决实际问题
1. 某超市花费750元购进草莓100千克,销售中有 的正常
损耗,为避免亏本(其他费用不考虑),售价至少定为每千
克多少元?设售价定为每千克 元,根据题意所列不等式正
确的是( )
A
A. B.
C. D.
2. 某人贷款2.2万元购进一台机器,生产某种产品.已知产品
的成本是每个5元,售价是每个8元,应付的税款和其他费用
是售价的 ,若每个月能生产、销售2 000个产品,问至
少几个月后能赚回这台机器的贷款?( )
B
A. 4 B. 5 C. 6 D. 7
【点拨】应付的税款和其他费用为
(元),每个月利润为
(元),
设 个月后能赚回这台机器的贷款,
则 ,
解得 .
所以至少5个月后能赚回这台机器的贷款.故选B.
3. [2024武汉江汉区三模] 从地向 地打长途电话,通话时
间不超过收费2.4元,超过 后每分钟加收1元.本题
中通话时间取整数,不足的通话时间按 计费.若小
江有10元钱,则他打一次电话最多可以通话的时间是( )
B
A. B. C. D.
【点拨】设他打一次电话可以通话的时间是 ,
根据题意得 ,
解得 .
为正整数, 的最大值为10.故选B.
4. [2024聊城东昌府区期末] 某市的出租车收费标准是:起步
价为6元(即行驶距离不超过3千米应付车费6元),超过3千
米后,每增加1千米加收1.4元(不足1千米按1千米收费).人
从甲地到乙地经过的路程是千米,出租车费为17.2元,则
为 ( )
B
A. 11 B.
C. 10 D.
【点拨】根据题意,得 ,
.故选B.
5. 黄河流域两岸地带培育的大红枣,学名“木
枣”,自古以来就被列为“五果”(桃、李、栗、杏、枣)之一.
某超市购进一批大红枣,一箱的进价为18元,标价为21元,
在春节期间,该超市准备打折销售,但要保证利润率不低于
,则至多可以打____折.
九
【点拨】设打折销售,由题意可得 ,
解得 ,
至多打九折.
6.[2024山西] 为加强校园消防安全,学校计划购买某种型号
的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为
540元/个,干粉灭火器的单价为380元/个.若学校购买这两种
灭火器的总价不超过21 000元,则最多可购买这种型号的水
基灭火器多少个?
【解】设可购买这种型号的水基灭火器 个,则购买干粉灭
火器 个,
根据题意得 ,
解得 .
为整数, 的最大值为12.
答:最多可购买这种型号的水基灭火器12个.
检验
设未知数
列不等式
数学问题
(一元一次不等式)
实际问题
(包含不等关系)
数学问题的解
(不等式的解集)
实际问题的答案
解不等式
同课章节目录
