人教版九上数学 22.2.2.2 二次函数y=a(x+h)?的图象和性质【课件】(23张PPT)
文档属性
| 名称 | 人教版九上数学 22.2.2.2 二次函数y=a(x+h)?的图象和性质【课件】(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第22章 二次函数与反比例函数 22.2.2
二次函数y=ax2+bx+c
的图象和性质
22.2.2.2 二次函数y=a(x+h) 的图象和性质
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
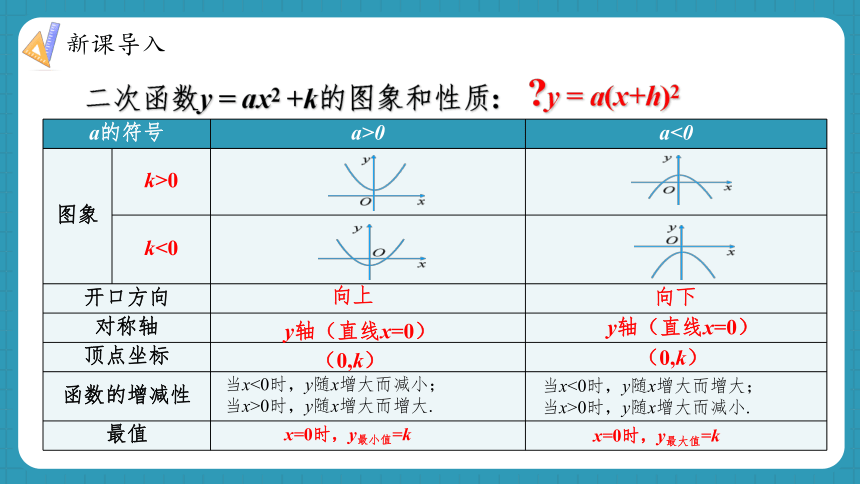
问题:说说二次函数y=ax2+k的图象的特征.
新课导入
a的符号 a>0 a<0
图象 k>0
k<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,k)
(0,k)
x=0时,y最小值=k
x=0时,y最大值=k
二次函数y = ax2 +k的图象和性质:
y = a(x+h)2
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
知识点1
二次函数y = a(x+h)2 的图象的画法
探究
解:先分别列表:
新课讲解
x … -2 -1 0 1 2 3 4 …
… -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
然后描点画图:
x … -4 -3 -2 -1 0 1 2 …
… -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
-8
-4
-2
y
-6
O
-2
2
x
4
-4
新课讲解
-8
-4
-2
y
-6
O
-2
2
x
4
-4
思考1 抛物线 , 的开口方向、对称轴和顶点各是什么?
新课讲解
开口方向 对称轴 顶点坐标
下
下
x=-1
x=1
(-1,0)
(1,0)
相同点:
不同点:
开口方向相同、形状相同。
对称轴、顶点坐标发生了改变。
知识点2
二次函数y = a(x+h)2 的图象和性质
-8
-4
-2
y
-6
O
-2
2
x
4
-4
记作x=-1
x=1
新课讲解
观察图象可发现:
把抛物线 平移 个单位就得到抛物线 ;把抛物线 平移 个单位就得到抛物线 .
所以, 的图象还可以由抛物线
平移 个单位得到.
向左
1
向右
1
向右
2
-8
-4
-2
y
-6
O
-2
2
x
4
-4
新课讲解
思考3 抛物线y = a(x+h)2 与抛物线y=ax2 有什么关系?
y
O
x
y = a(x+h)2 (h<0)
y = a(x+h)2 (h>0)
y = ax2
-h
-h
结论:
抛物线y=a(x+h)2的图象相当于把抛物线y=ax2的图象 (h>0)或 (h<0)平移 个单位.
向左
向右
|h|
新课讲解
二次函数y = a(x+h)2的图象和性质:
a的符号 a>0 a<0
图象 h<0
h>0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<-h时,y随x增大而增大;当x>-h时,y随x增大而减小.
当x<-h时,y随x增大而减小;当x>-h时,y随x增大而增大.
向上
向下
直线 x=-h
直线 x=-h
(-h,0)
x= -h时,y最小值= 0
x= -h时,y最大值= 0
(-h,0)
归纳小结
1.抛物线y=3(x-2)2可以由抛物线y=3x2向 平移 个单位得到.
2.二次函数y=-2(x-1)2的图象开口方向是 ,顶点坐标是 ,对称轴是 .
3.要得到抛物线y= (x-4)2,可将抛物线y= x2( )
A.向上平移4个单位 B.向下平移4个单位
C.向右平移4个单位 D.向左平移4个单位
右
2
向下
(1,0)
x=1
C
课堂练习
4.对于任意实数h,抛物线y=(x-h)2与抛物线y=x2( )
A.开口方向相同 B.对称轴相同
C.顶点相同 D.都有最高点
5.抛物线y= x2向左平移3个单位所得抛物线是( )
A.y= (x+3)2 B.y= (x-3)2
C.y= (x+3)2 D.y= (x-3)2
A
A
课堂练习
6.写出下列各组函数图象的开口方向、对称轴和顶点.
(1)y=- (x+2)2; (2)y=3(x-1)2.
解:(1)开口向下,对称轴为x=-2,顶点为(-2,0).
(2)开口向上,对称轴为x=1,顶点为(1,0).
课堂练习
7.在同一坐标系中,画出函数y=2x2与y=2(x-2)2的图象,分别指出两个图象之间的相互关系.
解:图象如图.
函数y=2(x-2)2的图象由函数y=2x2的图象向右平移2个单位得到.
y
O
x
y = 2(x-2)2
y = 2x2
2
课堂练习
8.在直角坐标系中画出函数y= (x-3)2的图象.
(1)指出该函数图象的开口方向、对称轴和顶点坐标;
(2)说明该函数图象与二次函数y= x2的图象的关系;
(3)根据图象说明,何时y随x的增大而减小,何时y随x的增大而增大,何时y有最大(小)值,是多少
课堂练习
解:(1)开口向上,对称轴为x=3,顶点坐标为(3,0).
(3)当x>3时,y随x的增大而增大,当x<3时,y随x的增大而减小,当x=3时,y有最小值,为0.
-2
2
4
y
O
-2
2
x
4
-4
(2)该函数图象由二次函数y= x2的图象向右平移3个单位得到.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
复习y=ax2+k
探索y=a(x+h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=-h
(-h,0)
a>0,开口向上
a<0,开口向下
y=ax2
h>0,向 平移 个单位
h<0,向 平移 个单位
左
| h |
右
| h |
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第22章 二次函数与反比例函数 22.2.2
二次函数y=ax2+bx+c
的图象和性质
22.2.2.2 二次函数y=a(x+h) 的图象和性质
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
问题:说说二次函数y=ax2+k的图象的特征.
新课导入
a的符号 a>0 a<0
图象 k>0
k<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,k)
(0,k)
x=0时,y最小值=k
x=0时,y最大值=k
二次函数y = ax2 +k的图象和性质:
y = a(x+h)2
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
知识点1
二次函数y = a(x+h)2 的图象的画法
探究
解:先分别列表:
新课讲解
x … -2 -1 0 1 2 3 4 …
… -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
然后描点画图:
x … -4 -3 -2 -1 0 1 2 …
… -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
-8
-4
-2
y
-6
O
-2
2
x
4
-4
新课讲解
-8
-4
-2
y
-6
O
-2
2
x
4
-4
思考1 抛物线 , 的开口方向、对称轴和顶点各是什么?
新课讲解
开口方向 对称轴 顶点坐标
下
下
x=-1
x=1
(-1,0)
(1,0)
相同点:
不同点:
开口方向相同、形状相同。
对称轴、顶点坐标发生了改变。
知识点2
二次函数y = a(x+h)2 的图象和性质
-8
-4
-2
y
-6
O
-2
2
x
4
-4
记作x=-1
x=1
新课讲解
观察图象可发现:
把抛物线 平移 个单位就得到抛物线 ;把抛物线 平移 个单位就得到抛物线 .
所以, 的图象还可以由抛物线
平移 个单位得到.
向左
1
向右
1
向右
2
-8
-4
-2
y
-6
O
-2
2
x
4
-4
新课讲解
思考3 抛物线y = a(x+h)2 与抛物线y=ax2 有什么关系?
y
O
x
y = a(x+h)2 (h<0)
y = a(x+h)2 (h>0)
y = ax2
-h
-h
结论:
抛物线y=a(x+h)2的图象相当于把抛物线y=ax2的图象 (h>0)或 (h<0)平移 个单位.
向左
向右
|h|
新课讲解
二次函数y = a(x+h)2的图象和性质:
a的符号 a>0 a<0
图象 h<0
h>0
开口方向
对称轴
顶点坐标
函数的增减性
最值
当x<-h时,y随x增大而增大;当x>-h时,y随x增大而减小.
当x<-h时,y随x增大而减小;当x>-h时,y随x增大而增大.
向上
向下
直线 x=-h
直线 x=-h
(-h,0)
x= -h时,y最小值= 0
x= -h时,y最大值= 0
(-h,0)
归纳小结
1.抛物线y=3(x-2)2可以由抛物线y=3x2向 平移 个单位得到.
2.二次函数y=-2(x-1)2的图象开口方向是 ,顶点坐标是 ,对称轴是 .
3.要得到抛物线y= (x-4)2,可将抛物线y= x2( )
A.向上平移4个单位 B.向下平移4个单位
C.向右平移4个单位 D.向左平移4个单位
右
2
向下
(1,0)
x=1
C
课堂练习
4.对于任意实数h,抛物线y=(x-h)2与抛物线y=x2( )
A.开口方向相同 B.对称轴相同
C.顶点相同 D.都有最高点
5.抛物线y= x2向左平移3个单位所得抛物线是( )
A.y= (x+3)2 B.y= (x-3)2
C.y= (x+3)2 D.y= (x-3)2
A
A
课堂练习
6.写出下列各组函数图象的开口方向、对称轴和顶点.
(1)y=- (x+2)2; (2)y=3(x-1)2.
解:(1)开口向下,对称轴为x=-2,顶点为(-2,0).
(2)开口向上,对称轴为x=1,顶点为(1,0).
课堂练习
7.在同一坐标系中,画出函数y=2x2与y=2(x-2)2的图象,分别指出两个图象之间的相互关系.
解:图象如图.
函数y=2(x-2)2的图象由函数y=2x2的图象向右平移2个单位得到.
y
O
x
y = 2(x-2)2
y = 2x2
2
课堂练习
8.在直角坐标系中画出函数y= (x-3)2的图象.
(1)指出该函数图象的开口方向、对称轴和顶点坐标;
(2)说明该函数图象与二次函数y= x2的图象的关系;
(3)根据图象说明,何时y随x的增大而减小,何时y随x的增大而增大,何时y有最大(小)值,是多少
课堂练习
解:(1)开口向上,对称轴为x=3,顶点坐标为(3,0).
(3)当x>3时,y随x的增大而增大,当x<3时,y随x的增大而减小,当x=3时,y有最小值,为0.
-2
2
4
y
O
-2
2
x
4
-4
(2)该函数图象由二次函数y= x2的图象向右平移3个单位得到.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
复习y=ax2+k
探索y=a(x+h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=-h
(-h,0)
a>0,开口向上
a<0,开口向下
y=ax2
h>0,向 平移 个单位
h<0,向 平移 个单位
左
| h |
右
| h |
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
