2024-2025学年人教版七下数学期中复习专题(图片版,无答案)
文档属性
| 名称 | 2024-2025学年人教版七下数学期中复习专题(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 09:01:18 | ||
图片预览



文档简介
期中备考习题集·目录
训练题(一)平行线与相交线中档题 1
训练题(二)平面直角坐标系中档题 5
训练题(三)实数中档题 9
训练题(四)新定义问题 11
训练题(五)找规律问题 13
训练题(六)网格作图题 17
训练题(七)实际应用题 21
训练题(八)平行线与相交线综合题 26
训练题(九)平面直角坐标系综合题 38
训练题(一) 平行线与相交线中档题
1.(23-24-青山区-期中-T8)下列命题中,真命题的个数有( )
①若 a=-b,则 3 a+ 3 b= 0;
②内错角相等;
③平行于同一条直线的两条直线互相平行;
④过一点有且只有一条直线与已知直线平行.
A. 3个 B. 2个 C. 1个 D. 0个
2.(23-24-东湖高新区-期中-T6)如图,图①是某品牌共享单车放在水平地面的实物图,
图②是其示意图,其中 AB,CD都与地面 l平行,∠BCD= 60°,∠BAC= 50°,当∠MAC
为( )度时,AM与CB平行.
A. 55 B. 60 C. 70 D. 75
3.(23-24-东湖高新区-期中-T8)如图,直线 AD,BE分别被直线 BF和 AC所截.∠1的
同位角、∠3的同旁内角和∠4的内错角的个数分别是( )
A. 2个,2个,2个 B. 2个,2个,1个
C. 3个,2个,2个 D. 3个,2个,1个
期中备考习题册·武汉 1
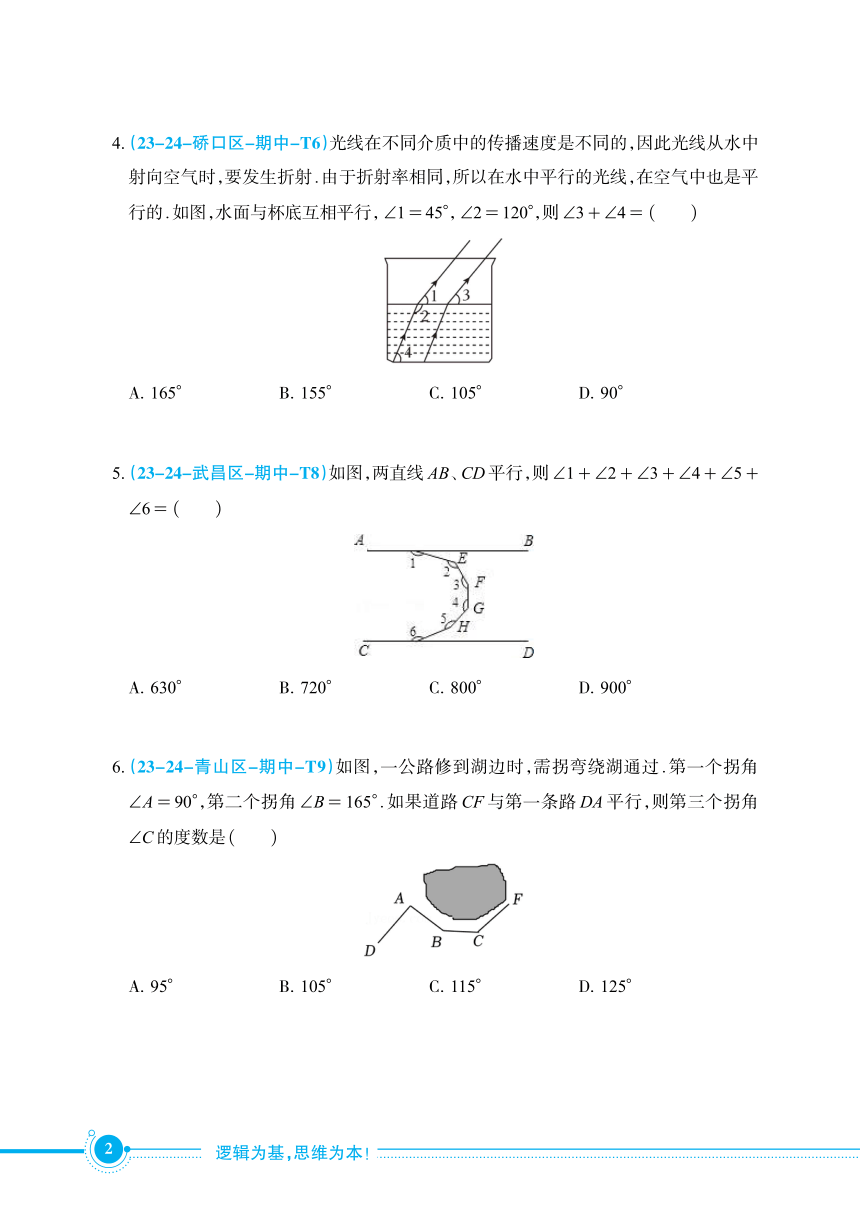
4.(23-24-硚口区-期中-T6)光线在不同介质中的传播速度是不同的,因此光线从水中
射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平
行的.如图,水面与杯底互相平行,∠1= 45°,∠2= 120°,则∠3+∠4= ( )
A. 165° B. 155° C. 105° D. 90°
5.(23-24-武昌区-期中-T8)如图,两直线 AB、CD平行,则∠1+∠2+∠3+∠4+∠5+
∠6= ( )
A. 630° B. 720° C. 800° D. 900°
6.(23-24-青山区-期中-T9)如图,一公路修到湖边时,需拐弯绕湖通过.第一个拐角
∠A= 90°,第二个拐角∠B= 165°.如果道路 CF与第一条路 DA平行,则第三个拐角
∠C的度数是( )
A. 95° B. 105° C. 115° D. 125°
2 逻辑为基,思维为本!
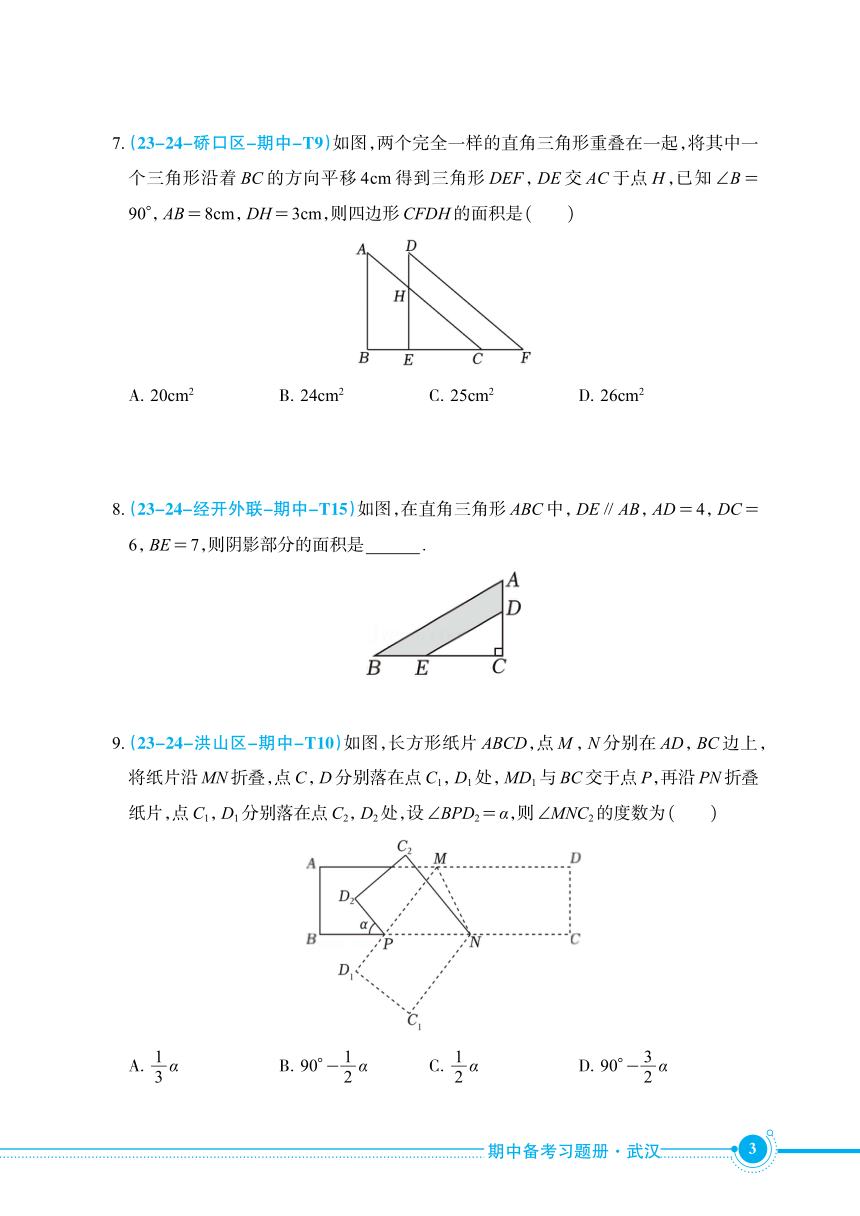
7.(23-24-硚口区-期中-T9)如图,两个完全一样的直角三角形重叠在一起,将其中一
个三角形沿着 BC的方向平移 4cm得到三角形 DEF,DE交 AC于点 H,已知∠B=
90°,AB= 8cm,DH= 3cm,则四边形CFDH的面积是( )
A. 20cm2 B. 24cm2 C. 25cm2 D. 26cm2
8.(23-24-经开外联-期中-T15)如图,在直角三角形 ABC中,DE∥ AB,AD= 4,DC=
6,BE= 7,则阴影部分的面积是 .
9.(23-24-洪山区-期中-T10)如图,长方形纸片 ABCD,点M,N分别在 AD,BC边上,
将纸片沿MN折叠,点C,D分别落在点C1,D1处,MD1与 BC交于点 P,再沿 PN折叠
纸片,点C1,D1分别落在点C2,D2处,设∠BPD2= α,则∠MNC2的度数为( )
A. 13 α B. 90° -
1 1 3
2 α C. 2 α D. 90° - 2 α
期中备考习题册·武汉 3
10.(23-24-经开外联-期中-T9)如图,将一张长方形纸条 ABCD沿 EF折叠,点 C,D分
别落在 C′,D′位置上,D′E与 AB的交点为M.若∠EFC= 114°,则∠D′MB的大小是
( )
A. 24° B. 42° C. 48° D. 52°
11.(23-24-洪山区-期中-T14)若∠1与∠2的两边分别平行,且∠1是∠2的余角的 4倍,
则∠1= .
12.(23-24-青山区-期中-T16)同一平面内∠A和∠B一组边互相平行,另一组边互相垂
直,若∠A=m°,∠B= n°,且m> n,则m和 n满足的数量关系为 .
4 逻辑为基,思维为本!
训练题(二) 平面直角坐标系中档题
1.(23-24-东湖高新区-期中-T9)下列命题中:
①若mn= 0,则点 A(m,n)在原点处;
②点(2,-m2)一定在第四象限;
③已知点 A(m,-n),点 B(m,n),m,n均不为 0,则直线 AB平行 y轴;
④已知点 A(n- 1,3),点 B(n+ 4,m),AB∥ x轴,则线段 AB的长为 5.
是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(23-24-东湖高新区-期中-T15)在平面直角坐标系中,若有两点 A(x1,y1),B(x2,
x +x y +yy2),利用平移知识可得到线段 AB中点的坐标为 1 2 , 1 22 2 .
请利用以上结论解决问题:若点 E(a,b),F(b,a- b),线段 EF的中点M恰好位于 y
轴上,且到 x轴的距离是 3,则点 E的坐标为 .
3.(23-24-洪山区-期中-T13)在平面直角坐标系中,点 P在第四象限,且 P到 x轴的距
离为 2,到 y轴的距离为 3,则点 P的坐标是 .
4.(23-24-江岸区-期中-T13)在平面直角坐标系中,点 A(m,-2),B(3,m- 1),且直
线 AB∥ x轴,则m的值是 .
期中备考习题册·武汉 5
5.(23-24-硚口区-期中-T8)已知 A(a,b),B两点关于 x轴对称,B,C两点关于 y轴对
称,则点C的坐标是( )
A.(a,-b) B.(-a,b) C.(-a,-b) D.(-b,-a)
6.(23-24-武珞路中学-期中-T14)在平面直角坐标系中,点 P(m- 5,m+ 1)在第二象
限,且点 P到 x轴的距离是到 y轴的距离的 2倍,则m的值是 .
7.(23-24-经开外联-期中-T14)在平面直角坐标系中,若点 P(6- 2a,a- 3)到 x轴的
距离为 3,则 a的值是 .
8.(23-24-武珞路中学-期中-T7)在平面直角坐标系中,线段 AB两端点的坐标分别为
A(-1,0),B(0,3),将线段 AB平移到线段 CD,其中一个对应点 C的坐标是(1,2),
则另一个对应点D的坐标是( )
A.(2,5) B.(-2,1)
C.(-2,1)或(2,5) D.(2,5)或(0,-1)
9.(23-24-武昌区-期中-T14)一个长方形在平面直角坐标系中三个顶点的坐标为(-1,
-1)、(-1,2)、(3,-1),则第四个顶点的坐标为 .
6 逻辑为基,思维为本!
10.(23-24-武昌区-期中-T9)已知点 P(x,y)到 x轴的距离为 2,到 y轴的距离为 3,且 x
+ y> 0,xy< 0,则点 P的坐标为( )
A.(-2,3) B.(2,3) C.(3,-2) D.(3,2)
11.(23-24-武昌区-期中-T15)如图,在平面直角坐标系中,已知长方形 ABCD的顶点坐
标:A(-4,-4),B(12,6),D(-8,2),CD与 y轴交于点 P,则 P点坐标为 .
12.(23-24-洪山区-期中-T15)已知点 O(0,0),B(2,1),点 A在 y轴正半轴上,且
S三角形OAB= 2,则点 A的坐标为 .
13.(23-24-武珞路中学-期中-T16)在平面直角坐标系中,A(2,3),B(6,1),P(x,y),
点 A、B、P在同一直线上,且 AP= 5BP,则 P点的坐标是 .
期中备考习题册·武汉 7
14.(23-24-江岸区-期中-T10)在平面直角坐标系中,已知点 A(m- 4,m+ 2),B(m-
4,m),C(m,0),D(2,0),已知三角形 ABD的面积是三角形 ABC面积的 2倍,则m
的值为( )
A. - 14 B. 2 C. - 14或 2 D. 14或-2
15.(23-24-经开外联-期中-T8)如图在平面直角坐标系中,点 A(2,3),点 B(-3,-2),
点C(4,-3),则三角形 ABC的面积是( )
A. 19 B. 20 C. 21 D. 21.5
8 逻辑为基,思维为本!
训练题(三) 实数中档题
1.(23-24-洪山区-期中-T8)有下列说法:
① 0.01是 0.1的一个平方根;
②-1的平方根是-1;
③ 0的平方根与算术平方根都是 0;
④无理数都是无限小数;
⑤所有实数都可以用数轴上的点表示,反过来,数轴上的所有点都表示实数.
其中正确的个数为( )
A. 2 B. 3 C. 4 D. 5
2.(23-24-江岸区-期中-T7)黄金分割数 5-12 是一个很奇妙的数,大量应用于艺术、
建筑和统计决策等方面,请你估算 5- 1的值( )
A. 在 1.1和 1.2之间 B. 在 1.2和 1.3之间
C. 在 1.3和 1.4之间 D. 在 1.4和 1.5之间
3.(23-24-江岸区-期中-T14)如图,圆的半径为 1个单位长度,该圆上仅有点 A与数轴
上表示-1的点重合,将圆沿数轴负方向滚动一周,点 A到达点 A'的位置,则点 A′表
示的数是 .
期中备考习题册·武汉 9
4.(23-24-硚口区-期中-T7)已知 a = 5,b = 2,c = 3,则 a、b、c的大小关系是
( )
A. b> a> c B. a> c> b C. a> b> c D. b> c> a
5.(23-24-武珞路中学-期中-T9)下列四个命题:①两条平行线被第三条直线所截,内
错角相等;②经过一点有且只有一条直线与已知直线垂直;③点 P(a- 2,2a+ 4)在 y
轴上,则 a= 2;④ 0.04的平方根是 0.2.其中是假命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.(23-24-经开外联-期中-T7) 7 的整数部分是 a, 17+32 的整数部分是 b,则 a、b
的大小关系是( )
A. a> b B. a= b C. a< b D. 无法确定
7.(23-24-青山区-期中-T7)若一个正数的两个不同的平方根分别是 3a- 4和-2a,则
这个数的立方根为( )
A. 8 B. 4 C. ± 4 D. 64
10 逻辑为基,思维为本!
训练题(四) 新定义问题
1.(23-24-东湖高新区-期中-T10)在平面直角坐标系中,设计了点的两种移动方式:
从点(x,y)移动到点(x+ 2,y+ 1)称为一次甲方式;
从点(x,y)移动到点(x+ 1,y+ 2)称为一次乙方式.
若点 P从原点O出发连续移动 10次,每次移动按甲方式或乙方式,最终移动到点 Q
(x,y),其中,按甲方式移动了m次,则 x+ y= ( )
A. m+ 10 B. m+ 20 C. 20-m D. 30
2.(23-24-江岸区-期中-T16)在平面直角坐标系 xOy中,对于不同的两点M,N,若点
M到 x轴,y轴的距离的较大值等于点 N到 x轴,y轴的距离的较大值,则称点M,N
互为“最距等点”.例如:点(3,-4),(4,-2)互为“最距等点”;点(3,-3),(-3,0)互为
“最距等点”.已知点 P(2- n,-2n+ 1)与点Q(n+ 1,2n- 3)互为“最距等点”,则 n
的值为 .
3.(23-24-洪山区-期中-T9)若用 [x]表示任意正实数的整数部分,例如:[2.5] = 2,[2]
= 2,[ 2 ] = 1,则式子 [ 2 ] - [ 3 ] + [ 4 ] - [ 5 ] + + [ 2022 ] - [ 2023 ] +
[ 2024]的值为( )(式子中的“+”,“-”依次相间)
A. 22 B. - 22 C. 23 D. - 23
期中备考习题册·武汉 11
4.(23-24-东湖高新区-期中-T23)数感和量感都是“数”的表达,二者密切相关,相互依
存.
(1) 2有多大呢?
完成下列问题.
在教材中“ 2有多大呢?”的探究活动,有同学是下面这样探究的.
我们知道面积是 2的正方形边长是 2,且因为 1.42= 1.96,1.52= 2.25,
所以 1.4< 2< 1.5.
设 2= 1.4+ x,画出示意图①.
由面积公式,可得 x2+ = 2.
因为 x值很小,所以 x2更小,略去 x2,
解方程得 x≈ (保留到 0.001),
即 2 ≈ .
(2)黄金分割数 5-12 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方
面,现在仿照上面探究“ 2有多大呢?”的过程,请你写出探究“ 5有多大”的过程,然
后计算出黄金分割数 5-12 的近似值.(结果均保留到 0.001)
(3)怎样画出 5?
教材中用两个面积为 1的小正方形分别沿对角线剪开,拼成一个面积为 2的大正方
形,如图②,可以求出大正方形的边长为 2;
现有 5个边长为 1的小正方形,排列形式如图③,类比图②的方法,请你在图③中用实
线把它们分割,然后在图④中拼接成一个新的大正方形.要求:在图③中画出分割线,
并在正方形网格图④中直接用实线画出拼接成的新的大正方形,且大正方形的边长
为 5.
12 逻辑为基,思维为本!
训练题(五) 找规律问题
1.(23-24-硚口区-期中-T16)在平面直角坐标系中,设计了点的两种移动方式:从点(x,y)
移动到点(x+ 2,y+ 1)称为一次甲方式,从点(x,y)移动到点(x+ 1,y+ 2)称为一次
乙方式.点 P从原点O出发连续移动 10次,每次移动按甲方式或乙方式,最终移动到
点 A(a,b),其中按甲方式移动了m次.则 a与 b满足的数量关系是 .
2.(23-24-东湖高新区-期中-T16)如图,已知四边形 ABCD的顶点为 A(1,2),B(-1,
2),C(-1,-2),D(1,-2),点 E是边 AB与 y轴的交点,点M从 E点出发,沿四边形
的边以 2单位长度 /s的速度逆时针做环绕匀速运动,当运动时间为 2024s时,此时点
M的坐标是 .
期中备考习题册·武汉 13
3.(23-24-青山区-期中-T10)如图,在平面直角坐标系中,长方形 ADCB的边 BC平行于
x轴,如果点 A的坐标为(-1,2),点 C的坐标为(3,-3),把一根长为 2024个单位长
度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A处,并按顺时针方向绕
在长方形 ADCB的边上,则细线的另一端所在位置的坐标为( )
A.(3,-2) B.(3,-3) C.(2,-3) D.(2,2)
4.(23-24-硚口区-期中-T10)如图,已知 a∥ b∥ c,点 P为 a与 b之间一点,过点 P作 9
条不同的直线均与直线 a相交,探究图中相交线形成的所有角中,互为对顶角的对数
是( )
A. 63 B. 90 C. 99 D. 126
14 逻辑为基,思维为本!
5.(23-24-经开外联-期中-T16)如图,在平面直角坐标系中,已知点 A(-3,0),B(0,
4),AB= 5,对三角形OAB连续做旋转变换,依次得到△1,△2,△3 ,则△2024的直角
顶点的纵坐标为 .
6.(23-24-江岸区-期中-T9)如图,在平面直角坐标系中,三角形 A1A2A3,三角形 A3A4A5,
三角形 A5A6A7, ,是斜边在 x轴上,斜边长分别为 2,4,6 的等腰直角三角形.
若三角形 A1A2A3的顶点坐标分别为 A1(2,0),A2(1,-1),A3(0,0),则依图中所示规
律,A2027的坐标为( )
A.(-1012,0) B.(1012,0) C.(1015,0) D.(-1015,0)
期中备考习题册·武汉 15
7.(23-24-武珞路中学-期中-T10)在平面直角坐标系中,横坐标、纵坐标都为整数的点
叫整点.如图,正方形内部和边上共有 25个整点,则过(100,0)(0,100)(-100,0)(0,
-100)四点围成的正方形边上和内部共有( )个整点.
A. 20200 B. 2020 C. 2021 D. 20201
8.(23-24-武昌区-期中-T10)如图,在平面直角坐标系上有点 A(1,0),点 A第一次跳
动至点 A1(-1,1),第二次点 A1向右跳到 A2(2,1),第三次点 A2跳到 A3(-2,2),第
四次点 A3向右跳动至点 A4(3,2), ,依此规律跳动下去,则点 A第 2022次跳动至
点 A2022的坐标为( )
A.(1012,1011) B.(1011,1010) C.(2022,2021) D.(1012,1010)
16 逻辑为基,思维为本!
训练题(六) 网格作图题
1.(23-24-东湖高新区-期中-T21)在平面直角坐标系中,已知点 A,B,C的坐标分别为
(-2,3),(-4,-1),(2,0).
(1)画出三角形 ABC;
(2)三角形 ABC中任意一点 P(x0,y0)
经平移后对应点为 P1(x0+ 4,y0- 1),
将三角形 ABC作同样的平移得到三角
形 A1B1C1,直接写出点 A1,B1的坐标;
(3)若点D在 x轴上,使三角形 ACD的
面积为 3,则点D的坐标为 ;
(4)仅用无刻度直尺在 AB边上画点 E,
连 CE,使三角形 BCE的面积为 8.(保
留画图痕迹)
2.(23-24-洪山区-期中-T21)如图,在平面直角坐标系中,A(-4,-2),B(-3,0),C
(-1,-3),三角形 ABC中任意一点 P(x0,y0)经平移后对应点为 P1(x0+ 4,y0+ 3),将
三角形 ABC作同样的平移得到三角形 A1B1C1.
(1)画出平移后的三角形 A1B1C1;
(2)线段 BC在平移的过程中扫过的面积为 ;
(3)连接 CC1,仅用无刻度直尺在线段 CC1上画点 D
使 A1D∥ BC;
(4)若 CC1= 5,点 E在直线 CC1上,则 BE的最小值
为 .
期中备考习题册·武汉 17
3.(23-24-江岸区-期中-T21)如图,在平面直角坐标系中,A(-4,-3),B(1,-1),C
(-2,3).
(1)三角形 ABC中任意一点 P(x0,y0)经平移后对
应点为 P'(x0+ 4,y0+ 3),将三角形 ABC作同样的
平移得到三角形 A'B'C'.画出平移后的三角形
A'B'C',写出 A'、B'、C' 的坐标:A' ,B'
,C' ;
(2)直接写出线段 BC与 x轴交点D的坐标 ;
(3)若将线段 CB沿水平方向平移一次,再竖直方
向平移一次,两次平移扫过的图形没有重叠部分.
两次平移后点 B的对应点 B′′的坐标为(1+ a,-1+ b),已知线段 CB扫过的面积为
20,请直接写出 a,b的数量关系: .
4.(23-24-硚口区-期中-T22)如图所示的方格中,每个小正方形的边长均为 1,每个小
正方形的顶点叫做格点,三角形 ABC的顶点都是格点,已知 AB= 5,依次解答下列问
题.
(1)将三角形 ABC平移后得到三角形 A'B'C',且点 A
的对应点为 A',画出三角形 A'B'C';
(2)画线段CD,使CD= AB且CD∥ AB;
(3)连接 A′D,B'C,直接写出四边形 A'B'CD的面积;
(4)P在直线 A'B'上,直接写出线段CP的最小值.
18 逻辑为基,思维为本!
5.(23-24-武珞路中学-期中-T21)在平面直角坐标系中,三角形 ABC的位置如图所示,
把△ABC平移后,三角形 ABC内任意一点 P(x,y)对应点为 P1(x+ 3,y- 2).
(1)画出平移后的图形;
(2)平移后得到三角形 A1B1C1各顶点的坐标分
别为 A1 ,B1 ,C1 .
(3)四边形 ABB1A1的面积是 .
(4)仅用无刻度直尺在 y轴上找一点D,使三角
形 ABD的面积等于 7.
6.(23-24-武昌区-期中-T20)作图题已知:如图,在平面直角坐标系中.
(1)作出△ABC向左平移 3个单位长度,向下平移 4个单位长度的△A1B1C1,并写出
△A1B1C1三个顶点的坐标:A1 ( ),B1 ( ),C1 ( );
(2)求四边形 ABB1A1的面积.
期中备考习题册·武汉 19
7.(23-24-经开外联-期中-T21)已知:如图,把△ABC向上平移 3个单位长度,再向右
平移 2个单位长度,得到△A′B′C′.
(1)写出 A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点 P在 y轴上,且 △BCP与 △ABC的
面积相等,求点 P的坐标.
8.(23-24-青山区-期中-T20)如图,由小正方形组成的 9× 10的网格,每个小正方形的
顶点叫做格点,三角形 ABC的三个顶点都是格点.
(1)请建立合适的平面直角坐标系,使点 A,B的坐标
分别是(3,4)和(7,2),并写出点C的坐标;
(2)在(1)的条件下,按要求完成画图或作答.
①将线段 AB先向左平移 5个单位长度,再向下平移
4个单位长度,得到线段 EF(其中 E,F分别是 A,B
的对应点),在图中画出线段 EF;
②将线段 AB平移得到线段 CD,其中点 C是点 B的
对应点,画出线段CD;
③在①②的条件下,连接OA,直接写出∠FEO,∠OAC,∠ACD,∠AOE这四个角之间
的数量关系.
20 逻辑为基,思维为本!
训练题(七) 实际应用题
1.(23-24-洪山区-期中-T19)根据如表回答下列问题:
x 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5
x2 16 16.81 17.64 18.49 19.36 20.25 21.16 22.09 23.04 24.01 25
(1)17.64的平方根是 , 18.5 ≈ ;
(2)物体自由下落的高度 h(单位:m)与下落时间 t(单位:s)的关系是 h= 4.9t2.有一
个物体从 99m高的建筑物上自由落下,物体到达地面需要多长时间?(请结合表中数
据精确到 0.1s)
2.(23-24-武昌区-期中-T21)如图,小明想用一块面积为 900cm2的正方形纸片,沿着边
的方向裁出一块面积为 800cm2的纸片,使它的长宽之比为 5:4,小明能用这块纸片裁
出符合要求的纸片吗?请通过计算说明.
期中备考习题册·武汉 21
3.(23-24-经开外联-期中-T22)如图,有一张长宽比为 3:2的长方形纸片 ABCD,面积
为 384cm2.
(1)求长方形纸片的长和宽;
(2)小丽想沿这张长方形纸片边的方向裁剪一块长宽比为 5:4的新长方形,使其面积
为 300cm2,请问她能裁出符合要求的长方形吗?试说明理由.
4.(23-24-江岸区-期中-T22)(1)如图,计划在空地上设计 3块并排的正方形基地做厂
房存放生产物资,基地总面积为 1200m2,则每块正方形基地的边长为 m.
(2)计划在厂房的东边围一个面积为 300m2的长方形基地,做仓库存放设备,仓库一
边靠在正方形的边上(计划与厂房共一面墙,且共用部分不超过正方形的边长,不考
虑门窗),另外三边用材料围成,并且它的长与宽之比为 5:2.若可以围成,请通过计
算设计出方案,并简要画出设计图;若不能围成,请通过计算说明理由.
22 逻辑为基,思维为本!
5.(23-24-武珞路中学-期中-T22)武汉市某路边开辟一块长方形荒地建设口袋公园,
已知这块地的长是宽的 2倍,面积是 800m2.
(1)求这块地的长和宽.
(2)现要在长方形地中建设一个圆形花圃和一个圆形喷泉,剩余部分铺上草坪,它们
的面积分别是 105πm2和 95πm2,试求出这两个圆形的半径,并判断是否符合要求?
期中备考习题册·武汉 23
6.(23-24-洪山区-期中-T22)如图所示的是一个潜望镜模型示意图,它由入射镜筒、直
管、反射镜筒以及两块平面镜构成,入射镜筒与反射镜筒互相平行,且都与直管垂直,
PQ,MN代表两块平面镜摆放的位置.镜筒上下壁和直管左右壁可视作分别相互平行
的直线.AB是进入潜望镜的光线,它与入射镜筒壁平行,与直管壁垂直,DE是离开
潜望镜的光线,光线经过镜子的反射时,满足入射角等于反射角的原理,如:∠ABP=
∠QBD,∠BDM=∠EDN.设∠HPQ= α,∠MNG= β.
(1)如图 1,当 PQ∥MN时,
①求证:AB∥DE;
②若光线 BD与直管壁平行,则 α的度数为 ;
(2)如图 2,当光线经过 B处镜面反射后照射到直管右壁 ST处时,若在 ST处放置一块
平面镜,使光线经平面镜上的点 C处反射到平面镜MN上的点 D处,并调整平面镜
MN的位置,使 AB∥DE.则此时 α与 β满足怎样的数量关系?并说明理由.
24 逻辑为基,思维为本!
7.(23-24-青山区-期中-T22)在图①中,将线段 A1A2向右平移 1个单位得到线段 B1B2,
从而得到封闭图形 A1A2B2B1(即阴影部分);在图②中,将折线 A1A2A3向右平移 1个单
位得到折线 B1B2B3,从而得到封闭图形 A1A2A3B3B2B1(即阴影部分).
(1)图①,图②图形中,除去阴影部分后,将剩余部分拼在一起就是如图③的图形,若
剩余部分的面积分别是 S1,S2(图①,图②长方形的长均为 a个单位,宽均为 b个单
位),则 S1= ,S2= ,S1 S2(填“>”或“=”或“<”);
(2)如图④,一块长方形场地由一条弯曲的小路和草地组成.这条弯曲的小路(即阴影
部分)任何地方的水平宽度都是 2m,除去小路部分后,空白部分表示的草地的图形可
拼在一起形成一个正方形,若这个正方形的面积是 70m2,则原长方形场地的长和宽分
别是多少m?
(3)如图⑤,一块长方形场地由两条弯曲的小路(阴影部分)和草地组成.竖直方向小
路任何地方的水平宽度都是 2m,水平方向小路任何地方的竖直宽度都是 1m.除去小
路部分后,空白部分表示草地的图形拼在一起形成一个长方形,且这个长方形的长是
宽的 2倍,面积是 70m2.计划用不超过 5200元的总费用将两条小路改铺成鹅卵石路
面,若每m2路面的铺设费用(人工费+材料费)约为 200元,请问总预算 5200元够吗?
并说明理由.
期中备考习题册·武汉 25
训练题(八) 平行线与相交线综合题
1.(23-24-洪山区-期中-T16)如图,AB ∥ CD,点 F在线段 AB上,点 E在线段 DF上,
∠CDQ= 3∠FDQ,∠QBE= 2∠ABQ,BQ交线段 EF于点 P,过点D作DH⊥ BQ于点
H.有下列结论:①∠BFD= 43 ∠CDQ,②∠BED+ 5∠FDQ= 3∠Q;③若∠FDH= 25°,
则∠BED-∠ABQ= 65°;④若∠CDH= 45°,则 BE ∥ DH.其中结论正确的有
(填写所有正确结论的序号).
2.(23-24-江岸区-期中-T15)如图,将长方形纸片 ABCD沿 EF折叠(折线 EF交 AD于
E,交 BC于 F),点C、D的落点分别是C'、D',ED'交 BC于G,再将四边形C′D′GF沿
FG折叠,点C'、D'的落点分别是C′′,D′′,GD′′交 EF于H,下列四个结论:①∠GEF
=∠GFE;② 2∠EFC=∠EGC+ 180°;③∠EGD′′ = 2∠EFG;④∠EHG= 3∠EFB.其中
正确的结论是 (填写序号).
26 逻辑为基,思维为本!
3.(23-24-经开外联-期中-T10)将直角三角板 EFG(∠G= 30°)和长方形直尺 ABCD按
如图方式叠放在一起,EG、AD交于点M,连接MF,∠BFE= α(0° < α< 60°),下列三
个结论:①若 ∠MFE = α,则 FG平分 ∠MFC;② ∠GMD = 60 ° -α;③若 FE平分
∠BFM,MF平分∠EMD,则 α= 40°,其中正确的结论有( )个.
A. 0 B. 1 C. 2 D. 3
4.(23-24-硚口区-期中-T15)如图,AD⊥ AB,DE平分∠ADC,CE平分∠DCB,∠1+
∠2= 90°,且∠1=∠DEF.下列四个结论:
① AD∥ BC;
②∠2=∠CEF;
③ 2∠1+∠DFE= 180°;
④∠DEA=∠CEB.
其中正确的结论是 (填写序号).
期中备考习题册·武汉 27
5.(23-24-武珞路中学-期中-T15)如图,在平面直角坐标系中,A(-3,0),B(0,4),
AB= 5,将直线 AB平移交坐标轴于 C、D点,BM平分∠ABO,DM平分∠ODC,过点
B作 BN⊥ BM交MD延长线于点 N,下列结论中:①∠BND= 45°;② BN平分∠CBH;
③点O到 AB的距离等于点O到CD的距离,都等于 125 ;④延长CD交 BN于点Q,则
CB=CQ.其中正确的有 .
6.(23-24-武昌区-期中-T16)如图,直线MN∥ PQ,点 A在直线MN与 PQ之间,点 B在
直线MN上,连接 AB.∠ABM的平分线 BC交 PQ于点 C,连接 AC,过点 A作 AD⊥
PQ交 PQ于点 D,作 AF⊥ AB交 PQ于点 F,AE平分∠DAF交 PQ于点 E,若∠CAE
= 50°,∠ACB= 52 ∠DAE,则∠ACD的度数是 .
28 逻辑为基,思维为本!
7.(23-24-青山区-期中-T15)如图,在△ABC中,∠BAC= 90°,AB= 6,AC= 8,BC=
10,将△ABC沿直线 BC向右平移 3个单位得到△DEF,连接 AD,则下列结论:
① AB∥DE,AB=DE;② ED⊥DF;③四边形 ABFD的周长是 27;④点 B到直线DF
的距离是 7.8.其中正确的是 .(填写序号)
期中备考习题册·武汉 29
8.(23-24-东湖高新区-期中-T22)学习平行线的性质与判定时,我们发现借助平行线
的“等角转化”可以解决许多问题.
(1)如图①,AB ∥ CD,点 P在 AB,CD内部,过点 P作 PE ∥ AB.请探究∠BPD,∠B,
∠D之间的数量关系,并证明.
(2)如图②,若点 P在 AB,CD外部,∠D=∠B+∠BPD,求证:AB∥CD;
(3)如图③,AB∥CD,∠ABP的角平分线 BE与∠CDP的角平分线DE相交于点 E,若
∠BPD= 70°,求∠BED的度数.
30 逻辑为基,思维为本!
9.(23-24-江岸区-期中-T23)【问题探究】(1)如图 1,AB ∥ CD,点 P在直线 AB上方
(∠AEP>∠CFP).
①请在拐点 P处作直线 AB的平行线;
②探究∠AEP、∠CFP、∠EPF之间的数量关系为 .
【问题拓展】(2)如图 2,AB∥CD,点 P在直线 AB上方,∠AEP的角平分线 EM所在的
直线和∠DFP的角平分线 FN所在的直线交于点 G(点G在直线 CD的下方),请写
出∠EPF和∠EGF之间的数量关系,并证明.
【问题迁移】(3)如图 3,AB ∥ CD,点 P在直线 AB上方,EG、ES、FM、FT分别是
∠AEP、∠BEP、∠CFP、∠DFP的三等分线,且 ∠AEG = ∠PES ∠MFP ∠DFT∠AEP ∠PEB = ∠CFP = ∠DFP
= 23 .直线 ES与直线 FM交于点M,直线 EG与直线 FT交于点 N(点 N在直线CD的
下方).设∠EMF-∠ENF= α,请直接写出 α与∠P的数量关系: .
期中备考习题册·武汉 31
10.(23-24-硚口区-期中-T23)已知 AB∥CD.
(1)如图 1,若 EK∥CD,求证:∠BEC-∠C+∠B= 180°;
(2)已知 BF平分∠ABE.
①如图 2,若 EG平分∠BEC,过点 B作 BH∥GE,判断∠FBH与∠C之间的数量关系,
并说明理由;
②如图 3,若CN平分∠ECD,BF的反向延长线和CN的反向延长线交于点M,且∠E
+∠M= 130°,直接写出∠E的大小.
32 逻辑为基,思维为本!
11.(23-24-武昌区-期中-T23)【问题原型】如图①和②,AB∥CD,点M在如图所在位置,
请分别写出图①和②中∠M、∠B、∠D之间的关系并选择一个结论进行证明;
(1)【推广应用】(1)如图③,AB∥CD,∠ABM邻补角的平分线 BN与∠CDM的角平分
线相交于点N,试探究∠M、∠N的数量关系并写出证明过程;
(2)如图③,AB∥CD,∠ABG和∠CDE的三等分角线交于点M,∠G= 64°,∠F= 6°,
∠E= 78°,求∠M的度数.
期中备考习题册·武汉 33
12.(23-24-经开外联-期中-T23)【问题情境】如图 1,AB ∥ CD,点 E在 CD下方,连接
BE、DE,∠B、∠D和∠BED的数量关系为 ,并给出证明;
【尝试应用】如图 2,AB ∥ CD,点 P为 AB与 CD之间的一点,点 Q在 CD下方,连接
BQ、PQ、DP,若∠D-∠Q= 30°,探究∠ABQ和∠DPQ的数量关系,并说明理由;
【拓广探索】如图 3,AB∥CD,MN与 AB、CD分别交于点 E、F,点 P在线段 EF上,点
G是直线 AB上一点,点 Q在 CD下方,连接 PG、GQ、QF,若 ∠PGQ = 3∠AGP,
∠NFQ= 3∠NFC,∠FPG- 2∠FQG= 18°,请直接写出∠FPG、∠FQG度数.
34 逻辑为基,思维为本!
13.(23-24-洪山区-期中-T23)如图,已知∠ABC= 70°,∠BAC= 40°,AD平分∠CAE.
(1)求证:AD∥ BC;
(2)若射线 AD绕点 A以每秒 1°的速度顺时针方向旋转得到 AM,同时,射线CA绕点
C以每秒 2°的速度顺时针方向旋转得到CN,AM和CN交于点 P,设旋转时间为 t秒.
①当 0< t< 55时,请写出∠APC与∠BAP之间的数量关系,并说明理由;
②当 0< t< 70时,若 15 ∠APC+∠BCP= 180°,请直接写出 t的值.
期中备考习题册·武汉 35
14.(23-24-武珞路中学-期中-T23)(1)【问题提出】如图(1),AB ∥ CD,点 P在直线 AB、
CD之间,且在直线 MN的右侧,点 M、N在直线 AB、CD上,探究 ∠MPN,∠BMP,
∠PND的数量关系.(此问无需写)
(2)【问题探究】①先将问题特殊化,如图(2),连MN,当MP平分 ∠BMN,NP平分
∠MND,直接写出∠MPN的大小.
②再探究一般情况,如图(1)当∠NMP=m∠BMP,∠MNP=m∠PND,求∠MPN的大
小.(用含m的式子表示)
(3)【问题拓展】如图(3),点 E是射线 NC上一动点,直线ME上有一点Q,连 NQ,当
∠QMP= n∠BMP,∠QNP= n∠DNP,且∠MPN= α°,∠PND-∠PMB= 20°时,直接
写出∠MQN的大小.(用含 n,α的式子表示)(题中所有角都是大于 0°且小于 180°的
角)
36 逻辑为基,思维为本!
15.(23-24-青山区-期中-T23)已知,在长方形 ABCD中,∠A=∠B=∠C=∠D= 90°,
AD∥ BC,AB ∥ CD,点 E在线段 AD上,点 F在线段 BC上,将长方形 ABCD沿 EF折
叠后,点D的对应点是M,点C的对应点是N.
(1)如图 1,若∠AEM= 36°,求∠EFB的度数;
(2)如图 2,将四边形 EMNF沿 BF继续折叠,点 N的对应点为 G,探索 ∠AEM与
∠GHF的数量关系,并证明你的结论;
(3)如图 3,P是直线MH和线段 AE的交点,将四边形 ABHP沿 PH折叠,点 A的对应
点是O,点 B的对应点是Q.请直接写出∠EFG和∠GHQ的数量关系.
期中备考习题册·武汉 37
训练题(九) 平面直角坐标系综合题
1.(23-24-东湖高新区-期中-T24)平面直角坐标系中,点 A的坐标为(a,0),2a- 16和
-9- a是某个正数的两个不同的平方根,第一象限的点 C到 y轴的距离为 23,且CB
⊥ y轴,垂足为 B,连 AC.
(1)直接写出点 A的坐标;
(2)如图①,点M、N分别为线段 BC、OA上的两个动点,点 N从点 A向原点O以 4个
单位长度 /秒的速度运动,同时点M从点 B向点 C以 2个单位长度 /秒的速度运动,
当点 N到达原点O时,点 N、M同时停止运动,设运动时间为 t,连接MN,当MN恰好
平分四边形 BOAC的面积时,求运动时间 t的值;(提示:梯形的面积等于(上底+下
底)×高÷ 2)
(3)如图②,在(2)中的点 N、M各自速度不变的条件下,线段MN与OC交于点D,若
CD 2
OD = 3 ,求点D的横坐标.
38 逻辑为基,思维为本!
2.(23-24-洪山区-期中-T24)在平面直角坐标系中,A(-5,a),B(b,5),C(c,n),且
a-1+(b+ 2) 2+ |2c+ 4| = 0.
(1)直接写出点 A,B的坐标及 c的值;
(2)如图 1,若三角形 ABC的面积为 9,求点C的坐标;
(3)如图 2,将线段 AB向右平移m个单位长度得到线段DE(点 A与D对应,点 B与 E
对应),若直线DE恰好经过点C,求m,n之间的数量关系.
期中备考习题册·武汉 39
3.(23-24-江岸区-期中-T24)在平面直角坐标系中,已知点 A(a,0),B(0,b),C(0,
-4),且 a和 b满足(a+ 4) 2+ 2-b = 0.将线段 AB平移,使得点 A、B分别与点 C、
D重合.
(1)请直接写出点 A、B、D的坐标:A ,B ,D ;
(2)如图 1,若点 P为直线 AB上一点,将点 P向右平移 t个单位到点 P',当点 P'在直
线CD上时,则 t的值为 ,若三角形COP'的面积是三角形DOP'的面积的 2倍,
请求出点 P的坐标;
(3)如图 2,若点Q(m,n)为平面直角坐标系内一点,且三角形 ABQ的面积是三角形
CDQ的面积的 2倍,请探究m,n的数量关系,并写出你的探究过程.
40 逻辑为基,思维为本!
4.(23-24-硚口区-期中-T24)如图 1,在平面直角坐标系中,点 A,B,C,D均在坐标轴
上,其坐标分别是 A(a,0),B(0,b),C(0,c),D(d,0),若 |a+ 4| + b-3 = 0,c<
0,d> 0,且∠ABO=∠DCO.
(1)求三角形 AOB的面积;
(2)求证:3d=-4c;
(3)如图 2,若 -3< c< 0,延长 CD到 Q,使 CQ = AB,线段 AQ交 y轴于点 K,求
BK-OK
OC 的值.
期中备考习题册·武汉 41
5.(23-24-武珞路中学-期中-T24)在平面直角坐标系中,点 A(a,4),点 B(6,b),且 a,
b满足 2a-4+(6- 3b) 2= 0.
(1)直接写出 a= ,b= ,三角形 AOB的面积是 .
(2)已知点C(n,-2)(0< n< 6),连接 AC交OB于点 P,若三角形 AOP的面积是 4,
求 n的值.
(3)现将线段 AB平移至线段CD,使点C、D分别在坐标轴上,且点 A的对应点是点C,
QO
点 B的对应点是点D,线段CD与直线OB相交于Q点,直接写出 QB 的值.
42 逻辑为基,思维为本!
6.(23-24-武昌区-期中-T24)如图,四边形 ABCD为正方形(各边相等),AB∥ y轴.已
知 B(a,0),C(b,0),P 1 22 a,m ,且 a+2+ |b- 1| +(m+ t- 4) = 0.
(1)求出点 B、C的坐标;
(2)点Q从C出发,以每秒 1个单位长度的速度沿射线CD方向运动,运动时间为 t秒,
①点 P在四边形 ABCD内部,且 S 7△BPQ= 2 时,求 t的值;
②当 S 1△BPQ= 2 S△BPC时,求 t的值.
期中备考习题册·武汉 43
7.(23-24-经开外联-期中-T24)如图,在平面直角坐标系中,A、B两点的坐标分别为
(a,0)、(0,b),其中 a、b满足 a+b+1 + |3- b| = 0,将线段 AB平移得到线段 CD,
其中点 A与点C对应,点C在 y轴负半轴上,点 B与点D对应,CD与 x轴交于点 E.
(1)点 A坐标 ;点 B坐标 ;三角形 AOB的面积为 ;
(2)若DE:CE= 1:2,
①求出点 E的坐标;
②求出点C、D的坐标;
(3)在(2)的条件下,点 P(t,0),t> 0,将点 P向右平移 1个单位,再向上平移 1个单
位得到点Q,连接 PC、PD、QA、QB,当三角形 ABQ的面积等于三角形CDP面积的 2
倍时,直接写出此时 t的值.
44 逻辑为基,思维为本!
8.(23-24-青山区-期中-T24)已知,三角形 ABC的顶点 A在 x轴的正半轴上,A,B,C
三点的坐标分别为 A(a,0),B(b,c),C(c- 1,c+ 1),且 a,b,c满足:|a- 5| +(b
- 4) 2= c-3+ 3-c.
(1)则 a= ,b= ,c= ;
(2)若D是 x轴上一点,三角形 ABD的面积是三角形 ABC面积的 6倍,求D点坐标;
(3)如图 2,点 F(2,0),E是线段 BC上一点,若直线 EF平分四边形 ABCO的面积,求
E点坐标.
期中备考习题册·武汉 45
训练题(一)平行线与相交线中档题 1
训练题(二)平面直角坐标系中档题 5
训练题(三)实数中档题 9
训练题(四)新定义问题 11
训练题(五)找规律问题 13
训练题(六)网格作图题 17
训练题(七)实际应用题 21
训练题(八)平行线与相交线综合题 26
训练题(九)平面直角坐标系综合题 38
训练题(一) 平行线与相交线中档题
1.(23-24-青山区-期中-T8)下列命题中,真命题的个数有( )
①若 a=-b,则 3 a+ 3 b= 0;
②内错角相等;
③平行于同一条直线的两条直线互相平行;
④过一点有且只有一条直线与已知直线平行.
A. 3个 B. 2个 C. 1个 D. 0个
2.(23-24-东湖高新区-期中-T6)如图,图①是某品牌共享单车放在水平地面的实物图,
图②是其示意图,其中 AB,CD都与地面 l平行,∠BCD= 60°,∠BAC= 50°,当∠MAC
为( )度时,AM与CB平行.
A. 55 B. 60 C. 70 D. 75
3.(23-24-东湖高新区-期中-T8)如图,直线 AD,BE分别被直线 BF和 AC所截.∠1的
同位角、∠3的同旁内角和∠4的内错角的个数分别是( )
A. 2个,2个,2个 B. 2个,2个,1个
C. 3个,2个,2个 D. 3个,2个,1个
期中备考习题册·武汉 1
4.(23-24-硚口区-期中-T6)光线在不同介质中的传播速度是不同的,因此光线从水中
射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平
行的.如图,水面与杯底互相平行,∠1= 45°,∠2= 120°,则∠3+∠4= ( )
A. 165° B. 155° C. 105° D. 90°
5.(23-24-武昌区-期中-T8)如图,两直线 AB、CD平行,则∠1+∠2+∠3+∠4+∠5+
∠6= ( )
A. 630° B. 720° C. 800° D. 900°
6.(23-24-青山区-期中-T9)如图,一公路修到湖边时,需拐弯绕湖通过.第一个拐角
∠A= 90°,第二个拐角∠B= 165°.如果道路 CF与第一条路 DA平行,则第三个拐角
∠C的度数是( )
A. 95° B. 105° C. 115° D. 125°
2 逻辑为基,思维为本!
7.(23-24-硚口区-期中-T9)如图,两个完全一样的直角三角形重叠在一起,将其中一
个三角形沿着 BC的方向平移 4cm得到三角形 DEF,DE交 AC于点 H,已知∠B=
90°,AB= 8cm,DH= 3cm,则四边形CFDH的面积是( )
A. 20cm2 B. 24cm2 C. 25cm2 D. 26cm2
8.(23-24-经开外联-期中-T15)如图,在直角三角形 ABC中,DE∥ AB,AD= 4,DC=
6,BE= 7,则阴影部分的面积是 .
9.(23-24-洪山区-期中-T10)如图,长方形纸片 ABCD,点M,N分别在 AD,BC边上,
将纸片沿MN折叠,点C,D分别落在点C1,D1处,MD1与 BC交于点 P,再沿 PN折叠
纸片,点C1,D1分别落在点C2,D2处,设∠BPD2= α,则∠MNC2的度数为( )
A. 13 α B. 90° -
1 1 3
2 α C. 2 α D. 90° - 2 α
期中备考习题册·武汉 3
10.(23-24-经开外联-期中-T9)如图,将一张长方形纸条 ABCD沿 EF折叠,点 C,D分
别落在 C′,D′位置上,D′E与 AB的交点为M.若∠EFC= 114°,则∠D′MB的大小是
( )
A. 24° B. 42° C. 48° D. 52°
11.(23-24-洪山区-期中-T14)若∠1与∠2的两边分别平行,且∠1是∠2的余角的 4倍,
则∠1= .
12.(23-24-青山区-期中-T16)同一平面内∠A和∠B一组边互相平行,另一组边互相垂
直,若∠A=m°,∠B= n°,且m> n,则m和 n满足的数量关系为 .
4 逻辑为基,思维为本!
训练题(二) 平面直角坐标系中档题
1.(23-24-东湖高新区-期中-T9)下列命题中:
①若mn= 0,则点 A(m,n)在原点处;
②点(2,-m2)一定在第四象限;
③已知点 A(m,-n),点 B(m,n),m,n均不为 0,则直线 AB平行 y轴;
④已知点 A(n- 1,3),点 B(n+ 4,m),AB∥ x轴,则线段 AB的长为 5.
是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(23-24-东湖高新区-期中-T15)在平面直角坐标系中,若有两点 A(x1,y1),B(x2,
x +x y +yy2),利用平移知识可得到线段 AB中点的坐标为 1 2 , 1 22 2 .
请利用以上结论解决问题:若点 E(a,b),F(b,a- b),线段 EF的中点M恰好位于 y
轴上,且到 x轴的距离是 3,则点 E的坐标为 .
3.(23-24-洪山区-期中-T13)在平面直角坐标系中,点 P在第四象限,且 P到 x轴的距
离为 2,到 y轴的距离为 3,则点 P的坐标是 .
4.(23-24-江岸区-期中-T13)在平面直角坐标系中,点 A(m,-2),B(3,m- 1),且直
线 AB∥ x轴,则m的值是 .
期中备考习题册·武汉 5
5.(23-24-硚口区-期中-T8)已知 A(a,b),B两点关于 x轴对称,B,C两点关于 y轴对
称,则点C的坐标是( )
A.(a,-b) B.(-a,b) C.(-a,-b) D.(-b,-a)
6.(23-24-武珞路中学-期中-T14)在平面直角坐标系中,点 P(m- 5,m+ 1)在第二象
限,且点 P到 x轴的距离是到 y轴的距离的 2倍,则m的值是 .
7.(23-24-经开外联-期中-T14)在平面直角坐标系中,若点 P(6- 2a,a- 3)到 x轴的
距离为 3,则 a的值是 .
8.(23-24-武珞路中学-期中-T7)在平面直角坐标系中,线段 AB两端点的坐标分别为
A(-1,0),B(0,3),将线段 AB平移到线段 CD,其中一个对应点 C的坐标是(1,2),
则另一个对应点D的坐标是( )
A.(2,5) B.(-2,1)
C.(-2,1)或(2,5) D.(2,5)或(0,-1)
9.(23-24-武昌区-期中-T14)一个长方形在平面直角坐标系中三个顶点的坐标为(-1,
-1)、(-1,2)、(3,-1),则第四个顶点的坐标为 .
6 逻辑为基,思维为本!
10.(23-24-武昌区-期中-T9)已知点 P(x,y)到 x轴的距离为 2,到 y轴的距离为 3,且 x
+ y> 0,xy< 0,则点 P的坐标为( )
A.(-2,3) B.(2,3) C.(3,-2) D.(3,2)
11.(23-24-武昌区-期中-T15)如图,在平面直角坐标系中,已知长方形 ABCD的顶点坐
标:A(-4,-4),B(12,6),D(-8,2),CD与 y轴交于点 P,则 P点坐标为 .
12.(23-24-洪山区-期中-T15)已知点 O(0,0),B(2,1),点 A在 y轴正半轴上,且
S三角形OAB= 2,则点 A的坐标为 .
13.(23-24-武珞路中学-期中-T16)在平面直角坐标系中,A(2,3),B(6,1),P(x,y),
点 A、B、P在同一直线上,且 AP= 5BP,则 P点的坐标是 .
期中备考习题册·武汉 7
14.(23-24-江岸区-期中-T10)在平面直角坐标系中,已知点 A(m- 4,m+ 2),B(m-
4,m),C(m,0),D(2,0),已知三角形 ABD的面积是三角形 ABC面积的 2倍,则m
的值为( )
A. - 14 B. 2 C. - 14或 2 D. 14或-2
15.(23-24-经开外联-期中-T8)如图在平面直角坐标系中,点 A(2,3),点 B(-3,-2),
点C(4,-3),则三角形 ABC的面积是( )
A. 19 B. 20 C. 21 D. 21.5
8 逻辑为基,思维为本!
训练题(三) 实数中档题
1.(23-24-洪山区-期中-T8)有下列说法:
① 0.01是 0.1的一个平方根;
②-1的平方根是-1;
③ 0的平方根与算术平方根都是 0;
④无理数都是无限小数;
⑤所有实数都可以用数轴上的点表示,反过来,数轴上的所有点都表示实数.
其中正确的个数为( )
A. 2 B. 3 C. 4 D. 5
2.(23-24-江岸区-期中-T7)黄金分割数 5-12 是一个很奇妙的数,大量应用于艺术、
建筑和统计决策等方面,请你估算 5- 1的值( )
A. 在 1.1和 1.2之间 B. 在 1.2和 1.3之间
C. 在 1.3和 1.4之间 D. 在 1.4和 1.5之间
3.(23-24-江岸区-期中-T14)如图,圆的半径为 1个单位长度,该圆上仅有点 A与数轴
上表示-1的点重合,将圆沿数轴负方向滚动一周,点 A到达点 A'的位置,则点 A′表
示的数是 .
期中备考习题册·武汉 9
4.(23-24-硚口区-期中-T7)已知 a = 5,b = 2,c = 3,则 a、b、c的大小关系是
( )
A. b> a> c B. a> c> b C. a> b> c D. b> c> a
5.(23-24-武珞路中学-期中-T9)下列四个命题:①两条平行线被第三条直线所截,内
错角相等;②经过一点有且只有一条直线与已知直线垂直;③点 P(a- 2,2a+ 4)在 y
轴上,则 a= 2;④ 0.04的平方根是 0.2.其中是假命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.(23-24-经开外联-期中-T7) 7 的整数部分是 a, 17+32 的整数部分是 b,则 a、b
的大小关系是( )
A. a> b B. a= b C. a< b D. 无法确定
7.(23-24-青山区-期中-T7)若一个正数的两个不同的平方根分别是 3a- 4和-2a,则
这个数的立方根为( )
A. 8 B. 4 C. ± 4 D. 64
10 逻辑为基,思维为本!
训练题(四) 新定义问题
1.(23-24-东湖高新区-期中-T10)在平面直角坐标系中,设计了点的两种移动方式:
从点(x,y)移动到点(x+ 2,y+ 1)称为一次甲方式;
从点(x,y)移动到点(x+ 1,y+ 2)称为一次乙方式.
若点 P从原点O出发连续移动 10次,每次移动按甲方式或乙方式,最终移动到点 Q
(x,y),其中,按甲方式移动了m次,则 x+ y= ( )
A. m+ 10 B. m+ 20 C. 20-m D. 30
2.(23-24-江岸区-期中-T16)在平面直角坐标系 xOy中,对于不同的两点M,N,若点
M到 x轴,y轴的距离的较大值等于点 N到 x轴,y轴的距离的较大值,则称点M,N
互为“最距等点”.例如:点(3,-4),(4,-2)互为“最距等点”;点(3,-3),(-3,0)互为
“最距等点”.已知点 P(2- n,-2n+ 1)与点Q(n+ 1,2n- 3)互为“最距等点”,则 n
的值为 .
3.(23-24-洪山区-期中-T9)若用 [x]表示任意正实数的整数部分,例如:[2.5] = 2,[2]
= 2,[ 2 ] = 1,则式子 [ 2 ] - [ 3 ] + [ 4 ] - [ 5 ] + + [ 2022 ] - [ 2023 ] +
[ 2024]的值为( )(式子中的“+”,“-”依次相间)
A. 22 B. - 22 C. 23 D. - 23
期中备考习题册·武汉 11
4.(23-24-东湖高新区-期中-T23)数感和量感都是“数”的表达,二者密切相关,相互依
存.
(1) 2有多大呢?
完成下列问题.
在教材中“ 2有多大呢?”的探究活动,有同学是下面这样探究的.
我们知道面积是 2的正方形边长是 2,且因为 1.42= 1.96,1.52= 2.25,
所以 1.4< 2< 1.5.
设 2= 1.4+ x,画出示意图①.
由面积公式,可得 x2+ = 2.
因为 x值很小,所以 x2更小,略去 x2,
解方程得 x≈ (保留到 0.001),
即 2 ≈ .
(2)黄金分割数 5-12 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方
面,现在仿照上面探究“ 2有多大呢?”的过程,请你写出探究“ 5有多大”的过程,然
后计算出黄金分割数 5-12 的近似值.(结果均保留到 0.001)
(3)怎样画出 5?
教材中用两个面积为 1的小正方形分别沿对角线剪开,拼成一个面积为 2的大正方
形,如图②,可以求出大正方形的边长为 2;
现有 5个边长为 1的小正方形,排列形式如图③,类比图②的方法,请你在图③中用实
线把它们分割,然后在图④中拼接成一个新的大正方形.要求:在图③中画出分割线,
并在正方形网格图④中直接用实线画出拼接成的新的大正方形,且大正方形的边长
为 5.
12 逻辑为基,思维为本!
训练题(五) 找规律问题
1.(23-24-硚口区-期中-T16)在平面直角坐标系中,设计了点的两种移动方式:从点(x,y)
移动到点(x+ 2,y+ 1)称为一次甲方式,从点(x,y)移动到点(x+ 1,y+ 2)称为一次
乙方式.点 P从原点O出发连续移动 10次,每次移动按甲方式或乙方式,最终移动到
点 A(a,b),其中按甲方式移动了m次.则 a与 b满足的数量关系是 .
2.(23-24-东湖高新区-期中-T16)如图,已知四边形 ABCD的顶点为 A(1,2),B(-1,
2),C(-1,-2),D(1,-2),点 E是边 AB与 y轴的交点,点M从 E点出发,沿四边形
的边以 2单位长度 /s的速度逆时针做环绕匀速运动,当运动时间为 2024s时,此时点
M的坐标是 .
期中备考习题册·武汉 13
3.(23-24-青山区-期中-T10)如图,在平面直角坐标系中,长方形 ADCB的边 BC平行于
x轴,如果点 A的坐标为(-1,2),点 C的坐标为(3,-3),把一根长为 2024个单位长
度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A处,并按顺时针方向绕
在长方形 ADCB的边上,则细线的另一端所在位置的坐标为( )
A.(3,-2) B.(3,-3) C.(2,-3) D.(2,2)
4.(23-24-硚口区-期中-T10)如图,已知 a∥ b∥ c,点 P为 a与 b之间一点,过点 P作 9
条不同的直线均与直线 a相交,探究图中相交线形成的所有角中,互为对顶角的对数
是( )
A. 63 B. 90 C. 99 D. 126
14 逻辑为基,思维为本!
5.(23-24-经开外联-期中-T16)如图,在平面直角坐标系中,已知点 A(-3,0),B(0,
4),AB= 5,对三角形OAB连续做旋转变换,依次得到△1,△2,△3 ,则△2024的直角
顶点的纵坐标为 .
6.(23-24-江岸区-期中-T9)如图,在平面直角坐标系中,三角形 A1A2A3,三角形 A3A4A5,
三角形 A5A6A7, ,是斜边在 x轴上,斜边长分别为 2,4,6 的等腰直角三角形.
若三角形 A1A2A3的顶点坐标分别为 A1(2,0),A2(1,-1),A3(0,0),则依图中所示规
律,A2027的坐标为( )
A.(-1012,0) B.(1012,0) C.(1015,0) D.(-1015,0)
期中备考习题册·武汉 15
7.(23-24-武珞路中学-期中-T10)在平面直角坐标系中,横坐标、纵坐标都为整数的点
叫整点.如图,正方形内部和边上共有 25个整点,则过(100,0)(0,100)(-100,0)(0,
-100)四点围成的正方形边上和内部共有( )个整点.
A. 20200 B. 2020 C. 2021 D. 20201
8.(23-24-武昌区-期中-T10)如图,在平面直角坐标系上有点 A(1,0),点 A第一次跳
动至点 A1(-1,1),第二次点 A1向右跳到 A2(2,1),第三次点 A2跳到 A3(-2,2),第
四次点 A3向右跳动至点 A4(3,2), ,依此规律跳动下去,则点 A第 2022次跳动至
点 A2022的坐标为( )
A.(1012,1011) B.(1011,1010) C.(2022,2021) D.(1012,1010)
16 逻辑为基,思维为本!
训练题(六) 网格作图题
1.(23-24-东湖高新区-期中-T21)在平面直角坐标系中,已知点 A,B,C的坐标分别为
(-2,3),(-4,-1),(2,0).
(1)画出三角形 ABC;
(2)三角形 ABC中任意一点 P(x0,y0)
经平移后对应点为 P1(x0+ 4,y0- 1),
将三角形 ABC作同样的平移得到三角
形 A1B1C1,直接写出点 A1,B1的坐标;
(3)若点D在 x轴上,使三角形 ACD的
面积为 3,则点D的坐标为 ;
(4)仅用无刻度直尺在 AB边上画点 E,
连 CE,使三角形 BCE的面积为 8.(保
留画图痕迹)
2.(23-24-洪山区-期中-T21)如图,在平面直角坐标系中,A(-4,-2),B(-3,0),C
(-1,-3),三角形 ABC中任意一点 P(x0,y0)经平移后对应点为 P1(x0+ 4,y0+ 3),将
三角形 ABC作同样的平移得到三角形 A1B1C1.
(1)画出平移后的三角形 A1B1C1;
(2)线段 BC在平移的过程中扫过的面积为 ;
(3)连接 CC1,仅用无刻度直尺在线段 CC1上画点 D
使 A1D∥ BC;
(4)若 CC1= 5,点 E在直线 CC1上,则 BE的最小值
为 .
期中备考习题册·武汉 17
3.(23-24-江岸区-期中-T21)如图,在平面直角坐标系中,A(-4,-3),B(1,-1),C
(-2,3).
(1)三角形 ABC中任意一点 P(x0,y0)经平移后对
应点为 P'(x0+ 4,y0+ 3),将三角形 ABC作同样的
平移得到三角形 A'B'C'.画出平移后的三角形
A'B'C',写出 A'、B'、C' 的坐标:A' ,B'
,C' ;
(2)直接写出线段 BC与 x轴交点D的坐标 ;
(3)若将线段 CB沿水平方向平移一次,再竖直方
向平移一次,两次平移扫过的图形没有重叠部分.
两次平移后点 B的对应点 B′′的坐标为(1+ a,-1+ b),已知线段 CB扫过的面积为
20,请直接写出 a,b的数量关系: .
4.(23-24-硚口区-期中-T22)如图所示的方格中,每个小正方形的边长均为 1,每个小
正方形的顶点叫做格点,三角形 ABC的顶点都是格点,已知 AB= 5,依次解答下列问
题.
(1)将三角形 ABC平移后得到三角形 A'B'C',且点 A
的对应点为 A',画出三角形 A'B'C';
(2)画线段CD,使CD= AB且CD∥ AB;
(3)连接 A′D,B'C,直接写出四边形 A'B'CD的面积;
(4)P在直线 A'B'上,直接写出线段CP的最小值.
18 逻辑为基,思维为本!
5.(23-24-武珞路中学-期中-T21)在平面直角坐标系中,三角形 ABC的位置如图所示,
把△ABC平移后,三角形 ABC内任意一点 P(x,y)对应点为 P1(x+ 3,y- 2).
(1)画出平移后的图形;
(2)平移后得到三角形 A1B1C1各顶点的坐标分
别为 A1 ,B1 ,C1 .
(3)四边形 ABB1A1的面积是 .
(4)仅用无刻度直尺在 y轴上找一点D,使三角
形 ABD的面积等于 7.
6.(23-24-武昌区-期中-T20)作图题已知:如图,在平面直角坐标系中.
(1)作出△ABC向左平移 3个单位长度,向下平移 4个单位长度的△A1B1C1,并写出
△A1B1C1三个顶点的坐标:A1 ( ),B1 ( ),C1 ( );
(2)求四边形 ABB1A1的面积.
期中备考习题册·武汉 19
7.(23-24-经开外联-期中-T21)已知:如图,把△ABC向上平移 3个单位长度,再向右
平移 2个单位长度,得到△A′B′C′.
(1)写出 A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点 P在 y轴上,且 △BCP与 △ABC的
面积相等,求点 P的坐标.
8.(23-24-青山区-期中-T20)如图,由小正方形组成的 9× 10的网格,每个小正方形的
顶点叫做格点,三角形 ABC的三个顶点都是格点.
(1)请建立合适的平面直角坐标系,使点 A,B的坐标
分别是(3,4)和(7,2),并写出点C的坐标;
(2)在(1)的条件下,按要求完成画图或作答.
①将线段 AB先向左平移 5个单位长度,再向下平移
4个单位长度,得到线段 EF(其中 E,F分别是 A,B
的对应点),在图中画出线段 EF;
②将线段 AB平移得到线段 CD,其中点 C是点 B的
对应点,画出线段CD;
③在①②的条件下,连接OA,直接写出∠FEO,∠OAC,∠ACD,∠AOE这四个角之间
的数量关系.
20 逻辑为基,思维为本!
训练题(七) 实际应用题
1.(23-24-洪山区-期中-T19)根据如表回答下列问题:
x 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5
x2 16 16.81 17.64 18.49 19.36 20.25 21.16 22.09 23.04 24.01 25
(1)17.64的平方根是 , 18.5 ≈ ;
(2)物体自由下落的高度 h(单位:m)与下落时间 t(单位:s)的关系是 h= 4.9t2.有一
个物体从 99m高的建筑物上自由落下,物体到达地面需要多长时间?(请结合表中数
据精确到 0.1s)
2.(23-24-武昌区-期中-T21)如图,小明想用一块面积为 900cm2的正方形纸片,沿着边
的方向裁出一块面积为 800cm2的纸片,使它的长宽之比为 5:4,小明能用这块纸片裁
出符合要求的纸片吗?请通过计算说明.
期中备考习题册·武汉 21
3.(23-24-经开外联-期中-T22)如图,有一张长宽比为 3:2的长方形纸片 ABCD,面积
为 384cm2.
(1)求长方形纸片的长和宽;
(2)小丽想沿这张长方形纸片边的方向裁剪一块长宽比为 5:4的新长方形,使其面积
为 300cm2,请问她能裁出符合要求的长方形吗?试说明理由.
4.(23-24-江岸区-期中-T22)(1)如图,计划在空地上设计 3块并排的正方形基地做厂
房存放生产物资,基地总面积为 1200m2,则每块正方形基地的边长为 m.
(2)计划在厂房的东边围一个面积为 300m2的长方形基地,做仓库存放设备,仓库一
边靠在正方形的边上(计划与厂房共一面墙,且共用部分不超过正方形的边长,不考
虑门窗),另外三边用材料围成,并且它的长与宽之比为 5:2.若可以围成,请通过计
算设计出方案,并简要画出设计图;若不能围成,请通过计算说明理由.
22 逻辑为基,思维为本!
5.(23-24-武珞路中学-期中-T22)武汉市某路边开辟一块长方形荒地建设口袋公园,
已知这块地的长是宽的 2倍,面积是 800m2.
(1)求这块地的长和宽.
(2)现要在长方形地中建设一个圆形花圃和一个圆形喷泉,剩余部分铺上草坪,它们
的面积分别是 105πm2和 95πm2,试求出这两个圆形的半径,并判断是否符合要求?
期中备考习题册·武汉 23
6.(23-24-洪山区-期中-T22)如图所示的是一个潜望镜模型示意图,它由入射镜筒、直
管、反射镜筒以及两块平面镜构成,入射镜筒与反射镜筒互相平行,且都与直管垂直,
PQ,MN代表两块平面镜摆放的位置.镜筒上下壁和直管左右壁可视作分别相互平行
的直线.AB是进入潜望镜的光线,它与入射镜筒壁平行,与直管壁垂直,DE是离开
潜望镜的光线,光线经过镜子的反射时,满足入射角等于反射角的原理,如:∠ABP=
∠QBD,∠BDM=∠EDN.设∠HPQ= α,∠MNG= β.
(1)如图 1,当 PQ∥MN时,
①求证:AB∥DE;
②若光线 BD与直管壁平行,则 α的度数为 ;
(2)如图 2,当光线经过 B处镜面反射后照射到直管右壁 ST处时,若在 ST处放置一块
平面镜,使光线经平面镜上的点 C处反射到平面镜MN上的点 D处,并调整平面镜
MN的位置,使 AB∥DE.则此时 α与 β满足怎样的数量关系?并说明理由.
24 逻辑为基,思维为本!
7.(23-24-青山区-期中-T22)在图①中,将线段 A1A2向右平移 1个单位得到线段 B1B2,
从而得到封闭图形 A1A2B2B1(即阴影部分);在图②中,将折线 A1A2A3向右平移 1个单
位得到折线 B1B2B3,从而得到封闭图形 A1A2A3B3B2B1(即阴影部分).
(1)图①,图②图形中,除去阴影部分后,将剩余部分拼在一起就是如图③的图形,若
剩余部分的面积分别是 S1,S2(图①,图②长方形的长均为 a个单位,宽均为 b个单
位),则 S1= ,S2= ,S1 S2(填“>”或“=”或“<”);
(2)如图④,一块长方形场地由一条弯曲的小路和草地组成.这条弯曲的小路(即阴影
部分)任何地方的水平宽度都是 2m,除去小路部分后,空白部分表示的草地的图形可
拼在一起形成一个正方形,若这个正方形的面积是 70m2,则原长方形场地的长和宽分
别是多少m?
(3)如图⑤,一块长方形场地由两条弯曲的小路(阴影部分)和草地组成.竖直方向小
路任何地方的水平宽度都是 2m,水平方向小路任何地方的竖直宽度都是 1m.除去小
路部分后,空白部分表示草地的图形拼在一起形成一个长方形,且这个长方形的长是
宽的 2倍,面积是 70m2.计划用不超过 5200元的总费用将两条小路改铺成鹅卵石路
面,若每m2路面的铺设费用(人工费+材料费)约为 200元,请问总预算 5200元够吗?
并说明理由.
期中备考习题册·武汉 25
训练题(八) 平行线与相交线综合题
1.(23-24-洪山区-期中-T16)如图,AB ∥ CD,点 F在线段 AB上,点 E在线段 DF上,
∠CDQ= 3∠FDQ,∠QBE= 2∠ABQ,BQ交线段 EF于点 P,过点D作DH⊥ BQ于点
H.有下列结论:①∠BFD= 43 ∠CDQ,②∠BED+ 5∠FDQ= 3∠Q;③若∠FDH= 25°,
则∠BED-∠ABQ= 65°;④若∠CDH= 45°,则 BE ∥ DH.其中结论正确的有
(填写所有正确结论的序号).
2.(23-24-江岸区-期中-T15)如图,将长方形纸片 ABCD沿 EF折叠(折线 EF交 AD于
E,交 BC于 F),点C、D的落点分别是C'、D',ED'交 BC于G,再将四边形C′D′GF沿
FG折叠,点C'、D'的落点分别是C′′,D′′,GD′′交 EF于H,下列四个结论:①∠GEF
=∠GFE;② 2∠EFC=∠EGC+ 180°;③∠EGD′′ = 2∠EFG;④∠EHG= 3∠EFB.其中
正确的结论是 (填写序号).
26 逻辑为基,思维为本!
3.(23-24-经开外联-期中-T10)将直角三角板 EFG(∠G= 30°)和长方形直尺 ABCD按
如图方式叠放在一起,EG、AD交于点M,连接MF,∠BFE= α(0° < α< 60°),下列三
个结论:①若 ∠MFE = α,则 FG平分 ∠MFC;② ∠GMD = 60 ° -α;③若 FE平分
∠BFM,MF平分∠EMD,则 α= 40°,其中正确的结论有( )个.
A. 0 B. 1 C. 2 D. 3
4.(23-24-硚口区-期中-T15)如图,AD⊥ AB,DE平分∠ADC,CE平分∠DCB,∠1+
∠2= 90°,且∠1=∠DEF.下列四个结论:
① AD∥ BC;
②∠2=∠CEF;
③ 2∠1+∠DFE= 180°;
④∠DEA=∠CEB.
其中正确的结论是 (填写序号).
期中备考习题册·武汉 27
5.(23-24-武珞路中学-期中-T15)如图,在平面直角坐标系中,A(-3,0),B(0,4),
AB= 5,将直线 AB平移交坐标轴于 C、D点,BM平分∠ABO,DM平分∠ODC,过点
B作 BN⊥ BM交MD延长线于点 N,下列结论中:①∠BND= 45°;② BN平分∠CBH;
③点O到 AB的距离等于点O到CD的距离,都等于 125 ;④延长CD交 BN于点Q,则
CB=CQ.其中正确的有 .
6.(23-24-武昌区-期中-T16)如图,直线MN∥ PQ,点 A在直线MN与 PQ之间,点 B在
直线MN上,连接 AB.∠ABM的平分线 BC交 PQ于点 C,连接 AC,过点 A作 AD⊥
PQ交 PQ于点 D,作 AF⊥ AB交 PQ于点 F,AE平分∠DAF交 PQ于点 E,若∠CAE
= 50°,∠ACB= 52 ∠DAE,则∠ACD的度数是 .
28 逻辑为基,思维为本!
7.(23-24-青山区-期中-T15)如图,在△ABC中,∠BAC= 90°,AB= 6,AC= 8,BC=
10,将△ABC沿直线 BC向右平移 3个单位得到△DEF,连接 AD,则下列结论:
① AB∥DE,AB=DE;② ED⊥DF;③四边形 ABFD的周长是 27;④点 B到直线DF
的距离是 7.8.其中正确的是 .(填写序号)
期中备考习题册·武汉 29
8.(23-24-东湖高新区-期中-T22)学习平行线的性质与判定时,我们发现借助平行线
的“等角转化”可以解决许多问题.
(1)如图①,AB ∥ CD,点 P在 AB,CD内部,过点 P作 PE ∥ AB.请探究∠BPD,∠B,
∠D之间的数量关系,并证明.
(2)如图②,若点 P在 AB,CD外部,∠D=∠B+∠BPD,求证:AB∥CD;
(3)如图③,AB∥CD,∠ABP的角平分线 BE与∠CDP的角平分线DE相交于点 E,若
∠BPD= 70°,求∠BED的度数.
30 逻辑为基,思维为本!
9.(23-24-江岸区-期中-T23)【问题探究】(1)如图 1,AB ∥ CD,点 P在直线 AB上方
(∠AEP>∠CFP).
①请在拐点 P处作直线 AB的平行线;
②探究∠AEP、∠CFP、∠EPF之间的数量关系为 .
【问题拓展】(2)如图 2,AB∥CD,点 P在直线 AB上方,∠AEP的角平分线 EM所在的
直线和∠DFP的角平分线 FN所在的直线交于点 G(点G在直线 CD的下方),请写
出∠EPF和∠EGF之间的数量关系,并证明.
【问题迁移】(3)如图 3,AB ∥ CD,点 P在直线 AB上方,EG、ES、FM、FT分别是
∠AEP、∠BEP、∠CFP、∠DFP的三等分线,且 ∠AEG = ∠PES ∠MFP ∠DFT∠AEP ∠PEB = ∠CFP = ∠DFP
= 23 .直线 ES与直线 FM交于点M,直线 EG与直线 FT交于点 N(点 N在直线CD的
下方).设∠EMF-∠ENF= α,请直接写出 α与∠P的数量关系: .
期中备考习题册·武汉 31
10.(23-24-硚口区-期中-T23)已知 AB∥CD.
(1)如图 1,若 EK∥CD,求证:∠BEC-∠C+∠B= 180°;
(2)已知 BF平分∠ABE.
①如图 2,若 EG平分∠BEC,过点 B作 BH∥GE,判断∠FBH与∠C之间的数量关系,
并说明理由;
②如图 3,若CN平分∠ECD,BF的反向延长线和CN的反向延长线交于点M,且∠E
+∠M= 130°,直接写出∠E的大小.
32 逻辑为基,思维为本!
11.(23-24-武昌区-期中-T23)【问题原型】如图①和②,AB∥CD,点M在如图所在位置,
请分别写出图①和②中∠M、∠B、∠D之间的关系并选择一个结论进行证明;
(1)【推广应用】(1)如图③,AB∥CD,∠ABM邻补角的平分线 BN与∠CDM的角平分
线相交于点N,试探究∠M、∠N的数量关系并写出证明过程;
(2)如图③,AB∥CD,∠ABG和∠CDE的三等分角线交于点M,∠G= 64°,∠F= 6°,
∠E= 78°,求∠M的度数.
期中备考习题册·武汉 33
12.(23-24-经开外联-期中-T23)【问题情境】如图 1,AB ∥ CD,点 E在 CD下方,连接
BE、DE,∠B、∠D和∠BED的数量关系为 ,并给出证明;
【尝试应用】如图 2,AB ∥ CD,点 P为 AB与 CD之间的一点,点 Q在 CD下方,连接
BQ、PQ、DP,若∠D-∠Q= 30°,探究∠ABQ和∠DPQ的数量关系,并说明理由;
【拓广探索】如图 3,AB∥CD,MN与 AB、CD分别交于点 E、F,点 P在线段 EF上,点
G是直线 AB上一点,点 Q在 CD下方,连接 PG、GQ、QF,若 ∠PGQ = 3∠AGP,
∠NFQ= 3∠NFC,∠FPG- 2∠FQG= 18°,请直接写出∠FPG、∠FQG度数.
34 逻辑为基,思维为本!
13.(23-24-洪山区-期中-T23)如图,已知∠ABC= 70°,∠BAC= 40°,AD平分∠CAE.
(1)求证:AD∥ BC;
(2)若射线 AD绕点 A以每秒 1°的速度顺时针方向旋转得到 AM,同时,射线CA绕点
C以每秒 2°的速度顺时针方向旋转得到CN,AM和CN交于点 P,设旋转时间为 t秒.
①当 0< t< 55时,请写出∠APC与∠BAP之间的数量关系,并说明理由;
②当 0< t< 70时,若 15 ∠APC+∠BCP= 180°,请直接写出 t的值.
期中备考习题册·武汉 35
14.(23-24-武珞路中学-期中-T23)(1)【问题提出】如图(1),AB ∥ CD,点 P在直线 AB、
CD之间,且在直线 MN的右侧,点 M、N在直线 AB、CD上,探究 ∠MPN,∠BMP,
∠PND的数量关系.(此问无需写)
(2)【问题探究】①先将问题特殊化,如图(2),连MN,当MP平分 ∠BMN,NP平分
∠MND,直接写出∠MPN的大小.
②再探究一般情况,如图(1)当∠NMP=m∠BMP,∠MNP=m∠PND,求∠MPN的大
小.(用含m的式子表示)
(3)【问题拓展】如图(3),点 E是射线 NC上一动点,直线ME上有一点Q,连 NQ,当
∠QMP= n∠BMP,∠QNP= n∠DNP,且∠MPN= α°,∠PND-∠PMB= 20°时,直接
写出∠MQN的大小.(用含 n,α的式子表示)(题中所有角都是大于 0°且小于 180°的
角)
36 逻辑为基,思维为本!
15.(23-24-青山区-期中-T23)已知,在长方形 ABCD中,∠A=∠B=∠C=∠D= 90°,
AD∥ BC,AB ∥ CD,点 E在线段 AD上,点 F在线段 BC上,将长方形 ABCD沿 EF折
叠后,点D的对应点是M,点C的对应点是N.
(1)如图 1,若∠AEM= 36°,求∠EFB的度数;
(2)如图 2,将四边形 EMNF沿 BF继续折叠,点 N的对应点为 G,探索 ∠AEM与
∠GHF的数量关系,并证明你的结论;
(3)如图 3,P是直线MH和线段 AE的交点,将四边形 ABHP沿 PH折叠,点 A的对应
点是O,点 B的对应点是Q.请直接写出∠EFG和∠GHQ的数量关系.
期中备考习题册·武汉 37
训练题(九) 平面直角坐标系综合题
1.(23-24-东湖高新区-期中-T24)平面直角坐标系中,点 A的坐标为(a,0),2a- 16和
-9- a是某个正数的两个不同的平方根,第一象限的点 C到 y轴的距离为 23,且CB
⊥ y轴,垂足为 B,连 AC.
(1)直接写出点 A的坐标;
(2)如图①,点M、N分别为线段 BC、OA上的两个动点,点 N从点 A向原点O以 4个
单位长度 /秒的速度运动,同时点M从点 B向点 C以 2个单位长度 /秒的速度运动,
当点 N到达原点O时,点 N、M同时停止运动,设运动时间为 t,连接MN,当MN恰好
平分四边形 BOAC的面积时,求运动时间 t的值;(提示:梯形的面积等于(上底+下
底)×高÷ 2)
(3)如图②,在(2)中的点 N、M各自速度不变的条件下,线段MN与OC交于点D,若
CD 2
OD = 3 ,求点D的横坐标.
38 逻辑为基,思维为本!
2.(23-24-洪山区-期中-T24)在平面直角坐标系中,A(-5,a),B(b,5),C(c,n),且
a-1+(b+ 2) 2+ |2c+ 4| = 0.
(1)直接写出点 A,B的坐标及 c的值;
(2)如图 1,若三角形 ABC的面积为 9,求点C的坐标;
(3)如图 2,将线段 AB向右平移m个单位长度得到线段DE(点 A与D对应,点 B与 E
对应),若直线DE恰好经过点C,求m,n之间的数量关系.
期中备考习题册·武汉 39
3.(23-24-江岸区-期中-T24)在平面直角坐标系中,已知点 A(a,0),B(0,b),C(0,
-4),且 a和 b满足(a+ 4) 2+ 2-b = 0.将线段 AB平移,使得点 A、B分别与点 C、
D重合.
(1)请直接写出点 A、B、D的坐标:A ,B ,D ;
(2)如图 1,若点 P为直线 AB上一点,将点 P向右平移 t个单位到点 P',当点 P'在直
线CD上时,则 t的值为 ,若三角形COP'的面积是三角形DOP'的面积的 2倍,
请求出点 P的坐标;
(3)如图 2,若点Q(m,n)为平面直角坐标系内一点,且三角形 ABQ的面积是三角形
CDQ的面积的 2倍,请探究m,n的数量关系,并写出你的探究过程.
40 逻辑为基,思维为本!
4.(23-24-硚口区-期中-T24)如图 1,在平面直角坐标系中,点 A,B,C,D均在坐标轴
上,其坐标分别是 A(a,0),B(0,b),C(0,c),D(d,0),若 |a+ 4| + b-3 = 0,c<
0,d> 0,且∠ABO=∠DCO.
(1)求三角形 AOB的面积;
(2)求证:3d=-4c;
(3)如图 2,若 -3< c< 0,延长 CD到 Q,使 CQ = AB,线段 AQ交 y轴于点 K,求
BK-OK
OC 的值.
期中备考习题册·武汉 41
5.(23-24-武珞路中学-期中-T24)在平面直角坐标系中,点 A(a,4),点 B(6,b),且 a,
b满足 2a-4+(6- 3b) 2= 0.
(1)直接写出 a= ,b= ,三角形 AOB的面积是 .
(2)已知点C(n,-2)(0< n< 6),连接 AC交OB于点 P,若三角形 AOP的面积是 4,
求 n的值.
(3)现将线段 AB平移至线段CD,使点C、D分别在坐标轴上,且点 A的对应点是点C,
QO
点 B的对应点是点D,线段CD与直线OB相交于Q点,直接写出 QB 的值.
42 逻辑为基,思维为本!
6.(23-24-武昌区-期中-T24)如图,四边形 ABCD为正方形(各边相等),AB∥ y轴.已
知 B(a,0),C(b,0),P 1 22 a,m ,且 a+2+ |b- 1| +(m+ t- 4) = 0.
(1)求出点 B、C的坐标;
(2)点Q从C出发,以每秒 1个单位长度的速度沿射线CD方向运动,运动时间为 t秒,
①点 P在四边形 ABCD内部,且 S 7△BPQ= 2 时,求 t的值;
②当 S 1△BPQ= 2 S△BPC时,求 t的值.
期中备考习题册·武汉 43
7.(23-24-经开外联-期中-T24)如图,在平面直角坐标系中,A、B两点的坐标分别为
(a,0)、(0,b),其中 a、b满足 a+b+1 + |3- b| = 0,将线段 AB平移得到线段 CD,
其中点 A与点C对应,点C在 y轴负半轴上,点 B与点D对应,CD与 x轴交于点 E.
(1)点 A坐标 ;点 B坐标 ;三角形 AOB的面积为 ;
(2)若DE:CE= 1:2,
①求出点 E的坐标;
②求出点C、D的坐标;
(3)在(2)的条件下,点 P(t,0),t> 0,将点 P向右平移 1个单位,再向上平移 1个单
位得到点Q,连接 PC、PD、QA、QB,当三角形 ABQ的面积等于三角形CDP面积的 2
倍时,直接写出此时 t的值.
44 逻辑为基,思维为本!
8.(23-24-青山区-期中-T24)已知,三角形 ABC的顶点 A在 x轴的正半轴上,A,B,C
三点的坐标分别为 A(a,0),B(b,c),C(c- 1,c+ 1),且 a,b,c满足:|a- 5| +(b
- 4) 2= c-3+ 3-c.
(1)则 a= ,b= ,c= ;
(2)若D是 x轴上一点,三角形 ABD的面积是三角形 ABC面积的 6倍,求D点坐标;
(3)如图 2,点 F(2,0),E是线段 BC上一点,若直线 EF平分四边形 ABCO的面积,求
E点坐标.
期中备考习题册·武汉 45
同课章节目录
