2025小升初六年级数学专题复习课件立体图形二圆柱和圆锥(共18张PPT)
文档属性
| 名称 | 2025小升初六年级数学专题复习课件立体图形二圆柱和圆锥(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 456.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 14:44:27 | ||
图片预览






文档简介
(共18张PPT)
2025小升初六年级数学专题复习
立体图形
——圆柱和圆锥
思维导图
(二)圆柱和圆锥
圆
柱
和
圆
锥
图示
圆柱
组成
容积与体积的计算方法相同,但
要从容器里面测量所需长度。
S 侧=2πrh,S 表=S 侧+2S 底=2πrh+2πr2
表面积
特征
体积
V=S 底 h=πr2h
(二)圆柱和圆锥
圆
柱
和
圆
锥
图示
圆锥
组成
容积与体积的计算方法相同,但
要从容器里面测量所需长度。
特征
体积
V= S 底 h= πr2h
■考点一 圆柱
考点清单
(二)圆柱和圆锥
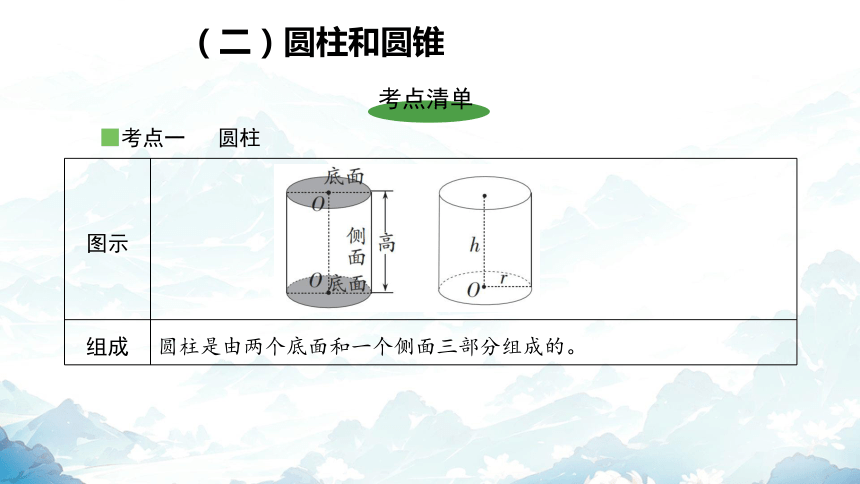
图示
组成 圆柱是由两个底面和一个侧面三部分组成的。
(二)圆柱和圆锥
特征 ①两个底面是完全相同的圆。
②有无数条高,所有的高都相等。
③侧面是一个曲面,沿高展开后是一个长方形或一个正方形。
表面积 S侧=2πrh,S表=S侧+2S底=2πrh+2πr2
体积 V=S底h=πr2h
容积 与体积的计算方法相同,但要从容器里面测量所需长度。
续表
(二)圆柱和圆锥
典例培优
一个圆柱形铁罐,从里面量得底面直径 6 cm,高 12 cm,在距铁罐口 3 cm 处破了一个洞,这个铁罐最多只能装水多少毫升?
(二)圆柱和圆锥
解析思路
规范作答 3.14×(6÷2)2×(12-3)=254.34(cm3)
254.34 cm3=254.34 mL
答:这个铁罐最多只能装水 254.34 mL。
方法点拨 求容器的容积时,要明确容器的高,如果容器破损,则容器底面到破损的最低处的距离才是能装物体的高。
(二)圆柱和圆锥
对应训练
1. 一个圆柱的底面半径是 1 dm,将它的侧面展开正好是一个正方形,这个圆柱的表面积是多少平方分米? 体积是多少立方分米?
(二)圆柱和圆锥
2. 一张长方形的铁皮(如图),剪下图中的阴影部分恰好可以做成一个油桶(接头处不算),这个油桶的容积是多少立方分米?
(二)圆柱和圆锥
■考点二 圆锥
图示
组成 圆锥是由一个底面和一个侧面两部分组成的。
特征 ①底面是一个圆。
②只有一条高。
③侧面是一个曲面,展开后是一个扇形。
(二)圆柱和圆锥
续表
表面积 S=6a2
体积 V= S底h= πr2h
容积 与体积的计算方法相同,但要从容器里面测量所需长度。
(二)圆柱和圆锥
典例培优
沙漏是古人用的一种计时仪器。下图这个沙漏里(装满沙子)的沙子一点点漏入下面空着的长方体木盒中,若沙子漏完了,均匀地铺在盒子中,那么在长方体木盒中会铺上大约多少厘米高的沙子呢?(结果保留两位小数)
(二)圆柱和圆锥
解析思路
规范作答
×3.14×(1.2÷2)2×1÷(3×2)=0.0628(dm)
0.0628 dm≈0.63 cm
答:在长方体木盒中会铺上大约 0.63 cm高的沙子。
(二)圆柱和圆锥
方法点拨
解决立体图形之间的转换问题时,要明确立体图形的容积、底面积和高之间的关系。
(二)圆柱和圆锥
对应训练
3. 一个正方体纸盒中恰好能放入一个体积为15.7 cm3 的圆锥,求正方体纸盒的体积。
(二)圆柱和圆锥
4. 下图圆柱的底面积是 113.04 cm2,从圆柱中挖去一个圆锥后,请计算剩余部分的体积。
(二)圆柱和圆锥
本版对应训练参考答案:
1.3.14×1×2=6.28(dm)
表面积:3.14×12×2+6.28×6.28=45.7184(dm2)
体积:3.14×12×6.28=19.7192(dm3)
2.d=20.56÷(1+1+3.14)=4(dm) 3.14×(4÷2)2×4=50.24(dm3)
3.解:设正方体纸盒的棱长为2a cm。
×3.14×a2×2a=15.7
a3=7.5
(2a)3=8a3=60(cm3)
(二)圆柱和圆锥
4. 圆锥:113.04×10× =376.8(cm3)
剩余部分:113.04×18-376.8=1657.92(cm3)
2025小升初六年级数学专题复习
立体图形
——圆柱和圆锥
思维导图
(二)圆柱和圆锥
圆
柱
和
圆
锥
图示
圆柱
组成
容积与体积的计算方法相同,但
要从容器里面测量所需长度。
S 侧=2πrh,S 表=S 侧+2S 底=2πrh+2πr2
表面积
特征
体积
V=S 底 h=πr2h
(二)圆柱和圆锥
圆
柱
和
圆
锥
图示
圆锥
组成
容积与体积的计算方法相同,但
要从容器里面测量所需长度。
特征
体积
V= S 底 h= πr2h
■考点一 圆柱
考点清单
(二)圆柱和圆锥
图示
组成 圆柱是由两个底面和一个侧面三部分组成的。
(二)圆柱和圆锥
特征 ①两个底面是完全相同的圆。
②有无数条高,所有的高都相等。
③侧面是一个曲面,沿高展开后是一个长方形或一个正方形。
表面积 S侧=2πrh,S表=S侧+2S底=2πrh+2πr2
体积 V=S底h=πr2h
容积 与体积的计算方法相同,但要从容器里面测量所需长度。
续表
(二)圆柱和圆锥
典例培优
一个圆柱形铁罐,从里面量得底面直径 6 cm,高 12 cm,在距铁罐口 3 cm 处破了一个洞,这个铁罐最多只能装水多少毫升?
(二)圆柱和圆锥
解析思路
规范作答 3.14×(6÷2)2×(12-3)=254.34(cm3)
254.34 cm3=254.34 mL
答:这个铁罐最多只能装水 254.34 mL。
方法点拨 求容器的容积时,要明确容器的高,如果容器破损,则容器底面到破损的最低处的距离才是能装物体的高。
(二)圆柱和圆锥
对应训练
1. 一个圆柱的底面半径是 1 dm,将它的侧面展开正好是一个正方形,这个圆柱的表面积是多少平方分米? 体积是多少立方分米?
(二)圆柱和圆锥
2. 一张长方形的铁皮(如图),剪下图中的阴影部分恰好可以做成一个油桶(接头处不算),这个油桶的容积是多少立方分米?
(二)圆柱和圆锥
■考点二 圆锥
图示
组成 圆锥是由一个底面和一个侧面两部分组成的。
特征 ①底面是一个圆。
②只有一条高。
③侧面是一个曲面,展开后是一个扇形。
(二)圆柱和圆锥
续表
表面积 S=6a2
体积 V= S底h= πr2h
容积 与体积的计算方法相同,但要从容器里面测量所需长度。
(二)圆柱和圆锥
典例培优
沙漏是古人用的一种计时仪器。下图这个沙漏里(装满沙子)的沙子一点点漏入下面空着的长方体木盒中,若沙子漏完了,均匀地铺在盒子中,那么在长方体木盒中会铺上大约多少厘米高的沙子呢?(结果保留两位小数)
(二)圆柱和圆锥
解析思路
规范作答
×3.14×(1.2÷2)2×1÷(3×2)=0.0628(dm)
0.0628 dm≈0.63 cm
答:在长方体木盒中会铺上大约 0.63 cm高的沙子。
(二)圆柱和圆锥
方法点拨
解决立体图形之间的转换问题时,要明确立体图形的容积、底面积和高之间的关系。
(二)圆柱和圆锥
对应训练
3. 一个正方体纸盒中恰好能放入一个体积为15.7 cm3 的圆锥,求正方体纸盒的体积。
(二)圆柱和圆锥
4. 下图圆柱的底面积是 113.04 cm2,从圆柱中挖去一个圆锥后,请计算剩余部分的体积。
(二)圆柱和圆锥
本版对应训练参考答案:
1.3.14×1×2=6.28(dm)
表面积:3.14×12×2+6.28×6.28=45.7184(dm2)
体积:3.14×12×6.28=19.7192(dm3)
2.d=20.56÷(1+1+3.14)=4(dm) 3.14×(4÷2)2×4=50.24(dm3)
3.解:设正方体纸盒的棱长为2a cm。
×3.14×a2×2a=15.7
a3=7.5
(2a)3=8a3=60(cm3)
(二)圆柱和圆锥
4. 圆锥:113.04×10× =376.8(cm3)
剩余部分:113.04×18-376.8=1657.92(cm3)
同课章节目录
