2025小升初六年级数学专题复习课件探索规律(共20张PPT)
文档属性
| 名称 | 2025小升初六年级数学专题复习课件探索规律(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 380.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
2025小升初六年级数学专题复习
探索规律
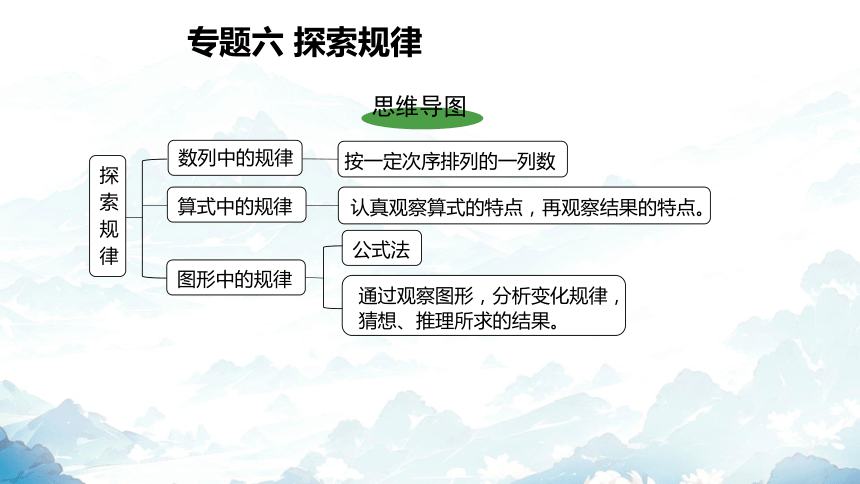
思维导图
专题六 探索规律
数列中的规律
认真观察算式的特点,再观察结果的特点。
按一定次序排列的一列数
算式中的规律
探
索
规
律
通过观察图形,分析变化规律,猜想、推理所求的结果。
图形中的规律
公式法
专题六 探索规律
方阵中的规律
实心方阵的数量关系:总数=最外层每边数×最外层每边数
探
索
规
律
四周数=(每边数-1)×4 每边数=四周数÷4+1
空心方阵的数量关系:总数=(最外层每边数-层数)×层数×4
搭配中的规律
加法原理
乘法原理
N=m1+m2+…+mn
N=m1×m2×…×mn
周期中的规律
关键是找出周期
■考点一 数列中的规律
考点清单
专题六 探索规律
定义 按一定次序排列的一列数。
常见 数列 ①规律蕴含在相邻两数的差或倍中;
②相邻两数中隐含规律;
③几项为一组,以组为单位找到规律;
④需要对数列进行分解,通过对比才能发现规律。
专题六 探索规律
典例培优
按规律填数: ( )、( )、 。
解析思路
专题六 探索规律
规范作答
方法点拨
根据分数中分母之间的关系、分子之间的关系,再综合思考整个分数之间的关系,找出规律,最后按规律解决问题。
专题六 探索规律
■考点二 算式中的规律
在数学算式中探索规律,应认真观察算式的特点,从而根据规律完成这一类题。
专题六 探索规律
典例培优 根据 3×4=12、33×34=1122、333×334=111222,推测 3333×3334=( )。
A. 11111222 B. 11122222
C. 11112222 D. 11111112
解析思路
两个因数的个位分别是 3 和 4,其他数位都是 3(除第一个算式外),每个因数增加一个3,则积分别增加一个 1 和一个 2,且 1 均在 2 的
左侧,且积中 1 和 2 的个数与因数的位数相同。
专题六 探索规律
规范作答 C
方法点拨
寻找数学算式的规律可以在算式的组成要素中去探索,也可以在算式的结果中去探索。
专题六 探索规律
■考点三 图形中的规律
1. 数图形的规律
数线段 的公式 (n-1)+…+2+1(n 为线段的总端点数)
数长方形 的公式 长边上的线段条数×宽边上的线段条数
数正方形 的公式 n2+(n-1)2+…+22+12(n 为正方形一边上的小格数)
专题六 探索规律
2. 图形的变化规律
先确定有几种图形,然后观察每种图形在不同组的位置变化,最后找出图形的排列规律。
(1)以组为单位按规律排列。
(2)同一组图形,通过不同的顺序排列。
(3)同一个图形通过平移或旋转排列。
3. 数与形结合的规律
在探索数与形结合的规律中,一方面需要考虑图形的特点,另一方面需要考虑数的排列规律。通过数形结合、对应等思想去解决问题。
专题六 探索规律
典例培优
一如图,按规律摆图形,第 n 个图形的周长是( )cm。(每个小正方形的边长是 1 cm)
A. 3n+4 B. 4n+2 C. 2n+4 D. 5n+2
解析思路
观察图形,几个长方形的宽不变,长分别是 1、2、3……即是第几个图形,长就是几,所以第 n 个图形的周长为 2(n+2)=2n+4。
规范作答 A
方法点拨 寻找数形结合的规律时,要先从图中找出变化的规律,再将其用算式表示出来。
专题六 探索规律
■考点四 方阵中的规律
类型 实心方阵 空心方阵
特点 方阵每边的人或物的数量相同;相邻两层,每边上的数量相差 2,即四边形四条边上的数量相差 8。 数量关系 相同点 四周数=(每边数-1)×4 每边数=四周数÷4+1 数量关系 不同点 总数=最外层每边数×最外层每边数 总数=(最外层每边数-层数)×层数×4
专题六 探索规律
典例培优
为迎接儿童节,学校举行团体操表演,六年级学生排成方阵,最外层每边站了 15 人,最外层一共有( )名学生。
解析思路
规范作答 56
方法点拨
判解决方阵问题时,要熟记数量关系。
专题六 探索规律
■考点五 搭配中的规律
搭配问题的解题思路类似于乘法原理,即完成一件事分成若干个步骤,每个步骤分别有 n1、n2、n3……种不同的方法,那么完成一件事情一共有 n1×n2×n3……种不同的方法。
专题六 探索规律
典例培优
如图,从甲地到丙地共有( )种不同
的行走路线。
解析思路
专题六 探索规律
规范作答 7
方法点拨
解决搭配问题时,要看题中给出的条件能否直接应用乘法,如果不能,可以分步计算。
专题六 探索规律
■考点六 周期中的规律
解答周期问题的关键是找出周期。 确定周期后用总量除以周期,如正好有整数个周期,结果为周期里的最后一个;如果比整数个周期多 n个,那么结果为下一个周期里的第 n 个;如果不是从第一个开始循环,可以从总数里减掉不是循环的个数后,再继续算。
专题六 探索规律
典例培优
一次大型运动会上,工作人员按照3 红 、 2 黄 、 1 绿 的 顺 序把气球穿起来装饰运动场,那么第 2022个气球是( )色的。
解析思路
气球按3 红、2 黄、1 绿排列,即 6 个气球为一组。 2022÷6=337(组),没有余数,则第2022 个气球是第 337 组的最后一个,是绿色的。
专题六 探索规律
规范作答 绿
方法点拨
解决周期问题时,关键是找到周期,然后用所求数据除以周期,如果没有余数,则是那一组的最后一个;如果有余数,则余数是几,所求就是
下一组的第几个。
2025小升初六年级数学专题复习
探索规律
思维导图
专题六 探索规律
数列中的规律
认真观察算式的特点,再观察结果的特点。
按一定次序排列的一列数
算式中的规律
探
索
规
律
通过观察图形,分析变化规律,猜想、推理所求的结果。
图形中的规律
公式法
专题六 探索规律
方阵中的规律
实心方阵的数量关系:总数=最外层每边数×最外层每边数
探
索
规
律
四周数=(每边数-1)×4 每边数=四周数÷4+1
空心方阵的数量关系:总数=(最外层每边数-层数)×层数×4
搭配中的规律
加法原理
乘法原理
N=m1+m2+…+mn
N=m1×m2×…×mn
周期中的规律
关键是找出周期
■考点一 数列中的规律
考点清单
专题六 探索规律
定义 按一定次序排列的一列数。
常见 数列 ①规律蕴含在相邻两数的差或倍中;
②相邻两数中隐含规律;
③几项为一组,以组为单位找到规律;
④需要对数列进行分解,通过对比才能发现规律。
专题六 探索规律
典例培优
按规律填数: ( )、( )、 。
解析思路
专题六 探索规律
规范作答
方法点拨
根据分数中分母之间的关系、分子之间的关系,再综合思考整个分数之间的关系,找出规律,最后按规律解决问题。
专题六 探索规律
■考点二 算式中的规律
在数学算式中探索规律,应认真观察算式的特点,从而根据规律完成这一类题。
专题六 探索规律
典例培优 根据 3×4=12、33×34=1122、333×334=111222,推测 3333×3334=( )。
A. 11111222 B. 11122222
C. 11112222 D. 11111112
解析思路
两个因数的个位分别是 3 和 4,其他数位都是 3(除第一个算式外),每个因数增加一个3,则积分别增加一个 1 和一个 2,且 1 均在 2 的
左侧,且积中 1 和 2 的个数与因数的位数相同。
专题六 探索规律
规范作答 C
方法点拨
寻找数学算式的规律可以在算式的组成要素中去探索,也可以在算式的结果中去探索。
专题六 探索规律
■考点三 图形中的规律
1. 数图形的规律
数线段 的公式 (n-1)+…+2+1(n 为线段的总端点数)
数长方形 的公式 长边上的线段条数×宽边上的线段条数
数正方形 的公式 n2+(n-1)2+…+22+12(n 为正方形一边上的小格数)
专题六 探索规律
2. 图形的变化规律
先确定有几种图形,然后观察每种图形在不同组的位置变化,最后找出图形的排列规律。
(1)以组为单位按规律排列。
(2)同一组图形,通过不同的顺序排列。
(3)同一个图形通过平移或旋转排列。
3. 数与形结合的规律
在探索数与形结合的规律中,一方面需要考虑图形的特点,另一方面需要考虑数的排列规律。通过数形结合、对应等思想去解决问题。
专题六 探索规律
典例培优
一如图,按规律摆图形,第 n 个图形的周长是( )cm。(每个小正方形的边长是 1 cm)
A. 3n+4 B. 4n+2 C. 2n+4 D. 5n+2
解析思路
观察图形,几个长方形的宽不变,长分别是 1、2、3……即是第几个图形,长就是几,所以第 n 个图形的周长为 2(n+2)=2n+4。
规范作答 A
方法点拨 寻找数形结合的规律时,要先从图中找出变化的规律,再将其用算式表示出来。
专题六 探索规律
■考点四 方阵中的规律
类型 实心方阵 空心方阵
特点 方阵每边的人或物的数量相同;相邻两层,每边上的数量相差 2,即四边形四条边上的数量相差 8。 数量关系 相同点 四周数=(每边数-1)×4 每边数=四周数÷4+1 数量关系 不同点 总数=最外层每边数×最外层每边数 总数=(最外层每边数-层数)×层数×4
专题六 探索规律
典例培优
为迎接儿童节,学校举行团体操表演,六年级学生排成方阵,最外层每边站了 15 人,最外层一共有( )名学生。
解析思路
规范作答 56
方法点拨
判解决方阵问题时,要熟记数量关系。
专题六 探索规律
■考点五 搭配中的规律
搭配问题的解题思路类似于乘法原理,即完成一件事分成若干个步骤,每个步骤分别有 n1、n2、n3……种不同的方法,那么完成一件事情一共有 n1×n2×n3……种不同的方法。
专题六 探索规律
典例培优
如图,从甲地到丙地共有( )种不同
的行走路线。
解析思路
专题六 探索规律
规范作答 7
方法点拨
解决搭配问题时,要看题中给出的条件能否直接应用乘法,如果不能,可以分步计算。
专题六 探索规律
■考点六 周期中的规律
解答周期问题的关键是找出周期。 确定周期后用总量除以周期,如正好有整数个周期,结果为周期里的最后一个;如果比整数个周期多 n个,那么结果为下一个周期里的第 n 个;如果不是从第一个开始循环,可以从总数里减掉不是循环的个数后,再继续算。
专题六 探索规律
典例培优
一次大型运动会上,工作人员按照3 红 、 2 黄 、 1 绿 的 顺 序把气球穿起来装饰运动场,那么第 2022个气球是( )色的。
解析思路
气球按3 红、2 黄、1 绿排列,即 6 个气球为一组。 2022÷6=337(组),没有余数,则第2022 个气球是第 337 组的最后一个,是绿色的。
专题六 探索规律
规范作答 绿
方法点拨
解决周期问题时,关键是找到周期,然后用所求数据除以周期,如果没有余数,则是那一组的最后一个;如果有余数,则余数是几,所求就是
下一组的第几个。
同课章节目录
