2025年中考数学一轮复习 15 四边形 小测验(含答案)
文档属性
| 名称 | 2025年中考数学一轮复习 15 四边形 小测验(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 15:33:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
15 四边形
分值:50分 时间30分钟
选择题(15分)
1、(2024·广东·模拟预测)若一个多边形的内角和是它的外角和的8倍,则该多边形的边数为( )
A.19 B.18 C.17 D.16
2、(2024·湖北·模拟预测)类比“赵爽弦图”,可类似的构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )
A. B. C. D.
3、(2024·广东·模拟预测)如图,D,E分别是 ABC的边,的中点,若 ADE的周长为6,则 ABC的周长为( )
A. B.3 C.12 D.36
4、(2024·广东·模拟预测)将一副三角尺在平行四边形按如图所示的方式摆放,设,则的度数为( )
A. B. C. D.
5、(2024·安徽·模拟预测)如图,矩形中,点在边上,平分,,分别是,的中点,,,则的值为( )
A. B. C. D.3
填空题(15分)
6、(2024·湖南·模拟预测)已知四边形的对角线垂直平分对角线于点,要使四边形为菱形,则可添加的条件是 (添加一个条件即可,不添加其他的点和线).
7、(2024·辽宁·中考真题)如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在直线上,若点的横坐标是8,为点的坐标为________
8、(2024·广东·模拟预测)如图,将一张长方形纸片沿折叠,使点A,B分别落在点,的位置.若,则 .
9、(2024·广西·中考真题)如图,两张宽度均为的纸条交叉叠放在一起,交叉形成的锐角为,则重合部分构成的四边形的周长为 .
10、(2024·陕西·模拟预测)如图,在矩形中,,在边上,,连接,则线段的最小长度为 .
简答题(20分)
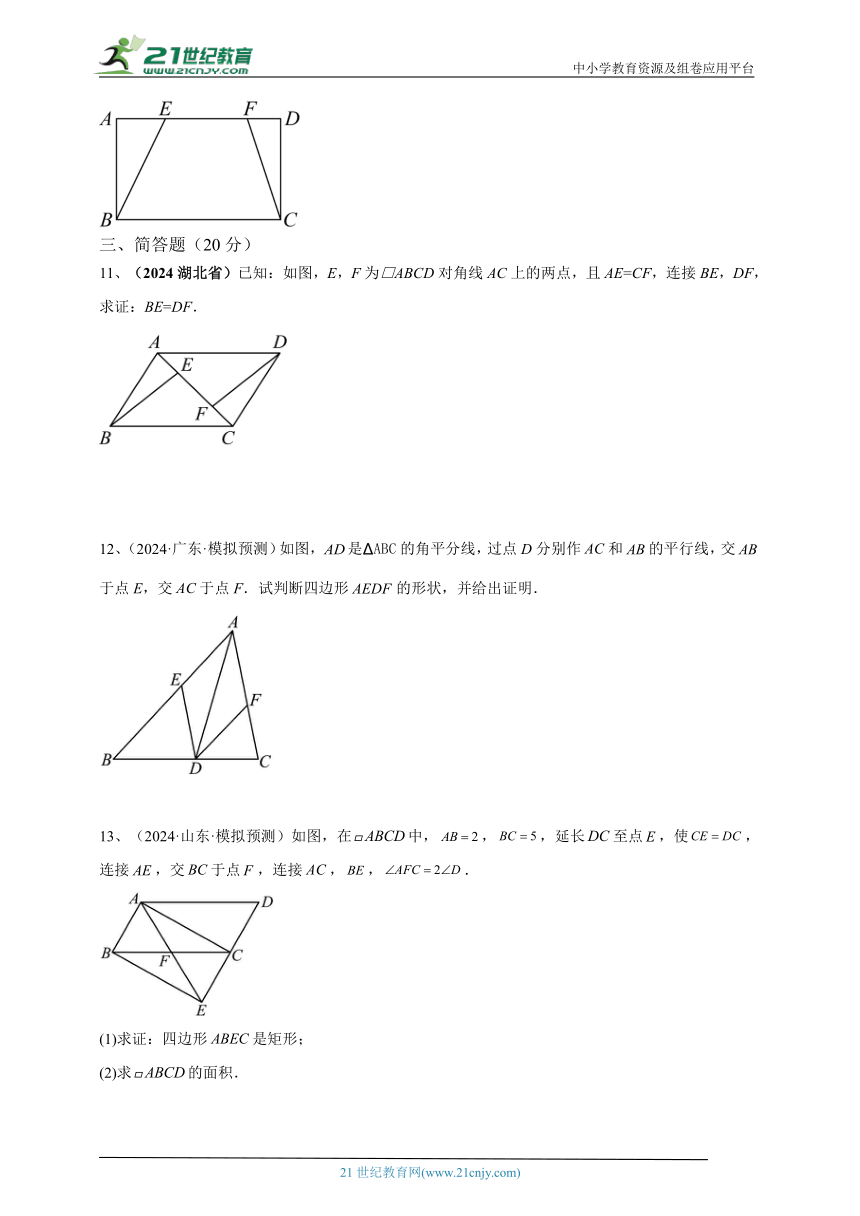
11、(2024湖北省)已知:如图,E,F为□ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
12、(2024·广东·模拟预测)如图,是 ABC的角平分线,过点D分别作和的平行线,交于点E,交于点F.试判断四边形的形状,并给出证明.
13、(2024·山东·模拟预测)如图,在中,,,延长至点,使,连接,交于点,连接,,.
(1)求证:四边形是矩形;
(2)求的面积.
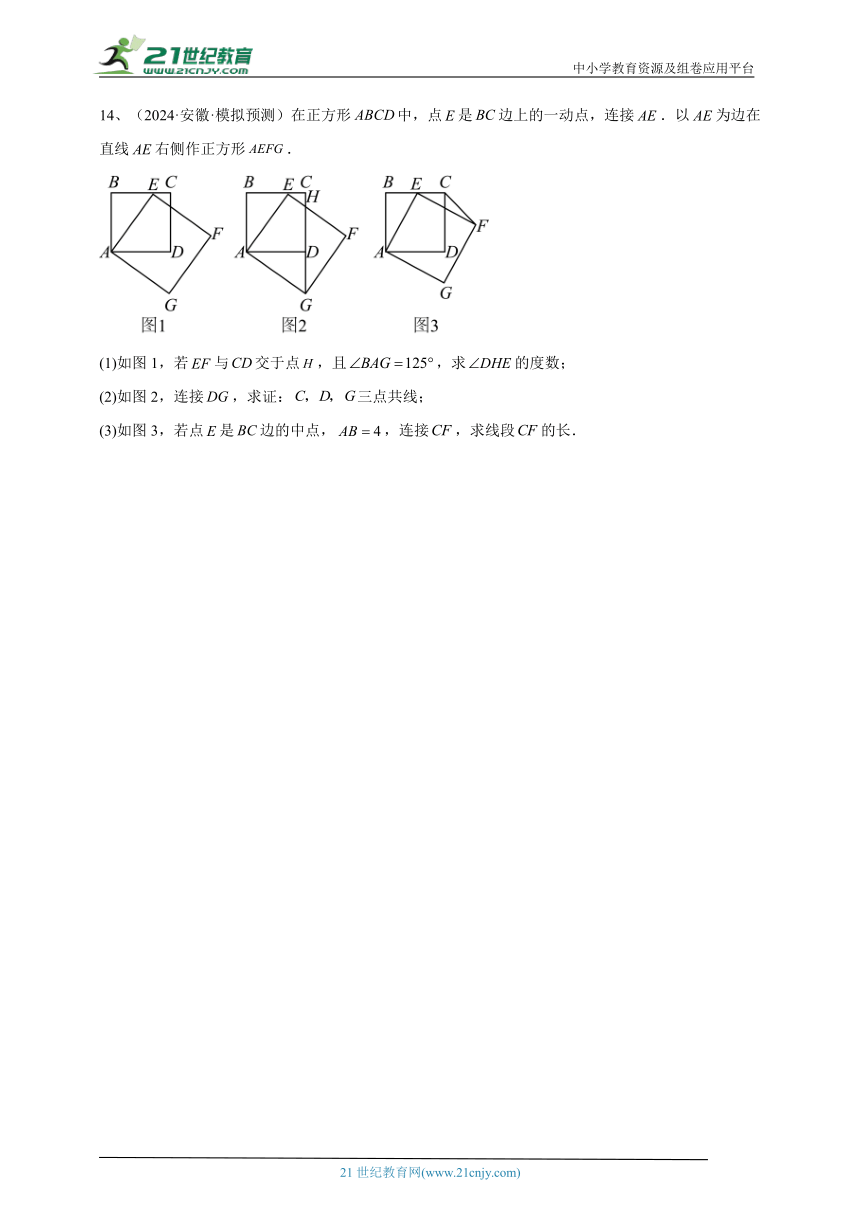
14、(2024·安徽·模拟预测)在正方形中,点是边上的一动点,连接.以为边在直线右侧作正方形.
(1)如图1,若与交于点,且,求的度数;
(2)如图2,连接,求证:三点共线;
(3)如图3,若点是边的中点,,连接,求线段的长.
答案:
一、选择题(15分)
1、(2024·广东·模拟预测)若一个多边形的内角和是它的外角和的8倍,则该多边形的边数为( )
A.19 B.18 C.17 D.16
解:设该多边形的边数为条,
则列方程为,
解得:,
故选B.
2、(2024·湖北·模拟预测)类比“赵爽弦图”,可类似的构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )
A. B. C. D.
解:如图所示,
正六边形的每个内角,
∴.
设,
∴,
根据勾股定理得.
根据题意可知,
∴.
作,交于点F,
∵是等边三角形,
∴.
根据勾股定理得,
∴,,
∴正六边形的面积,六个直角三角形的面积为,
∴此点取自小正六边形的概率是.
故选:A.
3、(2024·广东·模拟预测)如图,D,E分别是 ABC的边,的中点,若 ADE的周长为6,则 ABC的周长为( )
A. B.3 C.12 D.36
解:∵点分别是 ABC的边,的中点,
∴,即,
∵ ADE的周长为6,
∴,
∴的周长为,
故选:C.
4、(2024·广东·模拟预测)将一副三角尺在平行四边形按如图所示的方式摆放,设,则的度数为( )
A. B. C. D.
解:如图所示,过点G作,
由题意得,,则,
∴,
∴,,
∴,
∴,
故选:C.
5、(2024·安徽·模拟预测)如图,矩形中,点在边上,平分,,分别是,的中点,,,则的值为( )
A. B. C. D.3
解:四边形矩形,
∴,,
,
平分,
,
,
是等腰直角三角形,
,
是的中点,,
,
,
为的中点,,,
,
在中,,
,
,
,分别为,的中点,
是的中位线,
,
故选:D.
二、填空题(15分)
6、(2024·湖南·模拟预测)已知四边形的对角线垂直平分对角线于点,要使四边形为菱形,则可添加的条件是 (添加一个条件即可,不添加其他的点和线).
解:添加,理由如下:
∵四边形的对角线垂直平分对角线于点,
,
,
∴四边形是菱形,
故答案为:(答案不唯一).
7、(2024·辽宁·中考真题)如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在直线上,若点的横坐标是8,为点的坐标为________
解:过点B作轴,垂足为点D,
∵顶点在直线上,点的横坐标是8,
∴,即,
∴,
∵轴,
∴由勾股定理得:,
∵四边形是菱形,
∴轴,
∴将点B向左平移10个单位得到点C,
∴点,
8、(2024·广东·模拟预测)如图,将一张长方形纸片沿折叠,使点A,B分别落在点,的位置.若,则 .
解:∵四边形是矩形,
∴,
∴,
由折叠的性质得:,
∴,
故答案为:.
9、(2024·广西·中考真题)如图,两张宽度均为的纸条交叉叠放在一起,交叉形成的锐角为,则重合部分构成的四边形的周长为 .
解:过点作于,于,则,
∵两张纸条的对边平行,
∴,,
∴四边形是平行四边形,
又∵两张纸条的宽度相等,
∴,
∵,
∴,
∴四边形是菱形,
在中,,,
∴,
∴四边形的周长为,
故答案为:.
10、(2024·陕西·模拟预测)如图,在矩形中,,在边上,,连接,则线段的最小长度为 .
解:如图,取的中点,连接,作点关于的对称点,连接,
,
∵矩形中,,,
∴,,
∴四边形为平行四边形,
∴,即,
∵根据对称性可知,则,,
∵,
∴的最小长度:,
故答案为:.
三、简答题(20分)
11、(2024湖北省)已知:如图,E,F为□ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
解:利用SAS证明△AEB≌△CFD,再根据全等三角形的对应边相等即可得.
∵四边形ABCD是平行四边形,
∴AB//DC,AB=DC,
∴∠BAE=∠DCF,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(SAS),
∴BE=DF.
12、(2024·广东·模拟预测)如图,是的角平分线,过点D分别作和的平行线,交于点E,交于点F.试判断四边形的形状,并给出证明.
解:四边形是菱形,证明如下:
∵,
∴四边形是平行四边形,
∵是的角平分线,
∴,
又∵,
∴,
∴,
∴,
∴四边形是菱形.
13、(2024·山东·模拟预测)如图,在中,,,延长至点,使,连接,交于点,连接,,.
(1)求证:四边形是矩形;
(2)求的面积.
(1)证明:∵四边形是平行四边形,,
∴,,,
∵,
∴,
∴四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,
∴四边形是矩形;
(2)解:∵四边形是矩形,,,
∴,
∴,
∴,
∴的面积为.
14、(2024·安徽·模拟预测)在正方形中,点是边上的一动点,连接.以为边在直线右侧作正方形.
(1)如图1,若与交于点,且,求的度数;
(2)如图2,连接,求证:三点共线;
(3)如图3,若点是边的中点,,连接,求线段的长.
(1)解:在正方形中,;
在正方形中,,
,
,
则,
在四边形中,,
即,
则;
(2)证明:如图所示:
在正方形中,;
在正方形中,,
;;;;;
,
;;
,
,
即,
,
,即三点共线;
(3)解:过点作于点,如图所示:
,
在正方形中,;
在正方形中,,,
,
则,
在和中,
,
,
点是边的中点,,
,
则,
在中,,,
则由勾股定理可得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
15 四边形
分值:50分 时间30分钟
选择题(15分)
1、(2024·广东·模拟预测)若一个多边形的内角和是它的外角和的8倍,则该多边形的边数为( )
A.19 B.18 C.17 D.16
2、(2024·湖北·模拟预测)类比“赵爽弦图”,可类似的构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )
A. B. C. D.
3、(2024·广东·模拟预测)如图,D,E分别是 ABC的边,的中点,若 ADE的周长为6,则 ABC的周长为( )
A. B.3 C.12 D.36
4、(2024·广东·模拟预测)将一副三角尺在平行四边形按如图所示的方式摆放,设,则的度数为( )
A. B. C. D.
5、(2024·安徽·模拟预测)如图,矩形中,点在边上,平分,,分别是,的中点,,,则的值为( )
A. B. C. D.3
填空题(15分)
6、(2024·湖南·模拟预测)已知四边形的对角线垂直平分对角线于点,要使四边形为菱形,则可添加的条件是 (添加一个条件即可,不添加其他的点和线).
7、(2024·辽宁·中考真题)如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在直线上,若点的横坐标是8,为点的坐标为________
8、(2024·广东·模拟预测)如图,将一张长方形纸片沿折叠,使点A,B分别落在点,的位置.若,则 .
9、(2024·广西·中考真题)如图,两张宽度均为的纸条交叉叠放在一起,交叉形成的锐角为,则重合部分构成的四边形的周长为 .
10、(2024·陕西·模拟预测)如图,在矩形中,,在边上,,连接,则线段的最小长度为 .
简答题(20分)
11、(2024湖北省)已知:如图,E,F为□ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
12、(2024·广东·模拟预测)如图,是 ABC的角平分线,过点D分别作和的平行线,交于点E,交于点F.试判断四边形的形状,并给出证明.
13、(2024·山东·模拟预测)如图,在中,,,延长至点,使,连接,交于点,连接,,.
(1)求证:四边形是矩形;
(2)求的面积.
14、(2024·安徽·模拟预测)在正方形中,点是边上的一动点,连接.以为边在直线右侧作正方形.
(1)如图1,若与交于点,且,求的度数;
(2)如图2,连接,求证:三点共线;
(3)如图3,若点是边的中点,,连接,求线段的长.
答案:
一、选择题(15分)
1、(2024·广东·模拟预测)若一个多边形的内角和是它的外角和的8倍,则该多边形的边数为( )
A.19 B.18 C.17 D.16
解:设该多边形的边数为条,
则列方程为,
解得:,
故选B.
2、(2024·湖北·模拟预测)类比“赵爽弦图”,可类似的构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )
A. B. C. D.
解:如图所示,
正六边形的每个内角,
∴.
设,
∴,
根据勾股定理得.
根据题意可知,
∴.
作,交于点F,
∵是等边三角形,
∴.
根据勾股定理得,
∴,,
∴正六边形的面积,六个直角三角形的面积为,
∴此点取自小正六边形的概率是.
故选:A.
3、(2024·广东·模拟预测)如图,D,E分别是 ABC的边,的中点,若 ADE的周长为6,则 ABC的周长为( )
A. B.3 C.12 D.36
解:∵点分别是 ABC的边,的中点,
∴,即,
∵ ADE的周长为6,
∴,
∴的周长为,
故选:C.
4、(2024·广东·模拟预测)将一副三角尺在平行四边形按如图所示的方式摆放,设,则的度数为( )
A. B. C. D.
解:如图所示,过点G作,
由题意得,,则,
∴,
∴,,
∴,
∴,
故选:C.
5、(2024·安徽·模拟预测)如图,矩形中,点在边上,平分,,分别是,的中点,,,则的值为( )
A. B. C. D.3
解:四边形矩形,
∴,,
,
平分,
,
,
是等腰直角三角形,
,
是的中点,,
,
,
为的中点,,,
,
在中,,
,
,
,分别为,的中点,
是的中位线,
,
故选:D.
二、填空题(15分)
6、(2024·湖南·模拟预测)已知四边形的对角线垂直平分对角线于点,要使四边形为菱形,则可添加的条件是 (添加一个条件即可,不添加其他的点和线).
解:添加,理由如下:
∵四边形的对角线垂直平分对角线于点,
,
,
∴四边形是菱形,
故答案为:(答案不唯一).
7、(2024·辽宁·中考真题)如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在直线上,若点的横坐标是8,为点的坐标为________
解:过点B作轴,垂足为点D,
∵顶点在直线上,点的横坐标是8,
∴,即,
∴,
∵轴,
∴由勾股定理得:,
∵四边形是菱形,
∴轴,
∴将点B向左平移10个单位得到点C,
∴点,
8、(2024·广东·模拟预测)如图,将一张长方形纸片沿折叠,使点A,B分别落在点,的位置.若,则 .
解:∵四边形是矩形,
∴,
∴,
由折叠的性质得:,
∴,
故答案为:.
9、(2024·广西·中考真题)如图,两张宽度均为的纸条交叉叠放在一起,交叉形成的锐角为,则重合部分构成的四边形的周长为 .
解:过点作于,于,则,
∵两张纸条的对边平行,
∴,,
∴四边形是平行四边形,
又∵两张纸条的宽度相等,
∴,
∵,
∴,
∴四边形是菱形,
在中,,,
∴,
∴四边形的周长为,
故答案为:.
10、(2024·陕西·模拟预测)如图,在矩形中,,在边上,,连接,则线段的最小长度为 .
解:如图,取的中点,连接,作点关于的对称点,连接,
,
∵矩形中,,,
∴,,
∴四边形为平行四边形,
∴,即,
∵根据对称性可知,则,,
∵,
∴的最小长度:,
故答案为:.
三、简答题(20分)
11、(2024湖北省)已知:如图,E,F为□ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
解:利用SAS证明△AEB≌△CFD,再根据全等三角形的对应边相等即可得.
∵四边形ABCD是平行四边形,
∴AB//DC,AB=DC,
∴∠BAE=∠DCF,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(SAS),
∴BE=DF.
12、(2024·广东·模拟预测)如图,是的角平分线,过点D分别作和的平行线,交于点E,交于点F.试判断四边形的形状,并给出证明.
解:四边形是菱形,证明如下:
∵,
∴四边形是平行四边形,
∵是的角平分线,
∴,
又∵,
∴,
∴,
∴,
∴四边形是菱形.
13、(2024·山东·模拟预测)如图,在中,,,延长至点,使,连接,交于点,连接,,.
(1)求证:四边形是矩形;
(2)求的面积.
(1)证明:∵四边形是平行四边形,,
∴,,,
∵,
∴,
∴四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,
∴四边形是矩形;
(2)解:∵四边形是矩形,,,
∴,
∴,
∴,
∴的面积为.
14、(2024·安徽·模拟预测)在正方形中,点是边上的一动点,连接.以为边在直线右侧作正方形.
(1)如图1,若与交于点,且,求的度数;
(2)如图2,连接,求证:三点共线;
(3)如图3,若点是边的中点,,连接,求线段的长.
(1)解:在正方形中,;
在正方形中,,
,
,
则,
在四边形中,,
即,
则;
(2)证明:如图所示:
在正方形中,;
在正方形中,,
;;;;;
,
;;
,
,
即,
,
,即三点共线;
(3)解:过点作于点,如图所示:
,
在正方形中,;
在正方形中,,,
,
则,
在和中,
,
,
点是边的中点,,
,
则,
在中,,,
则由勾股定理可得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
