2025年中考数学一轮复习 16 相似三角形 小测验(含答案)
文档属性
| 名称 | 2025年中考数学一轮复习 16 相似三角形 小测验(含答案) | 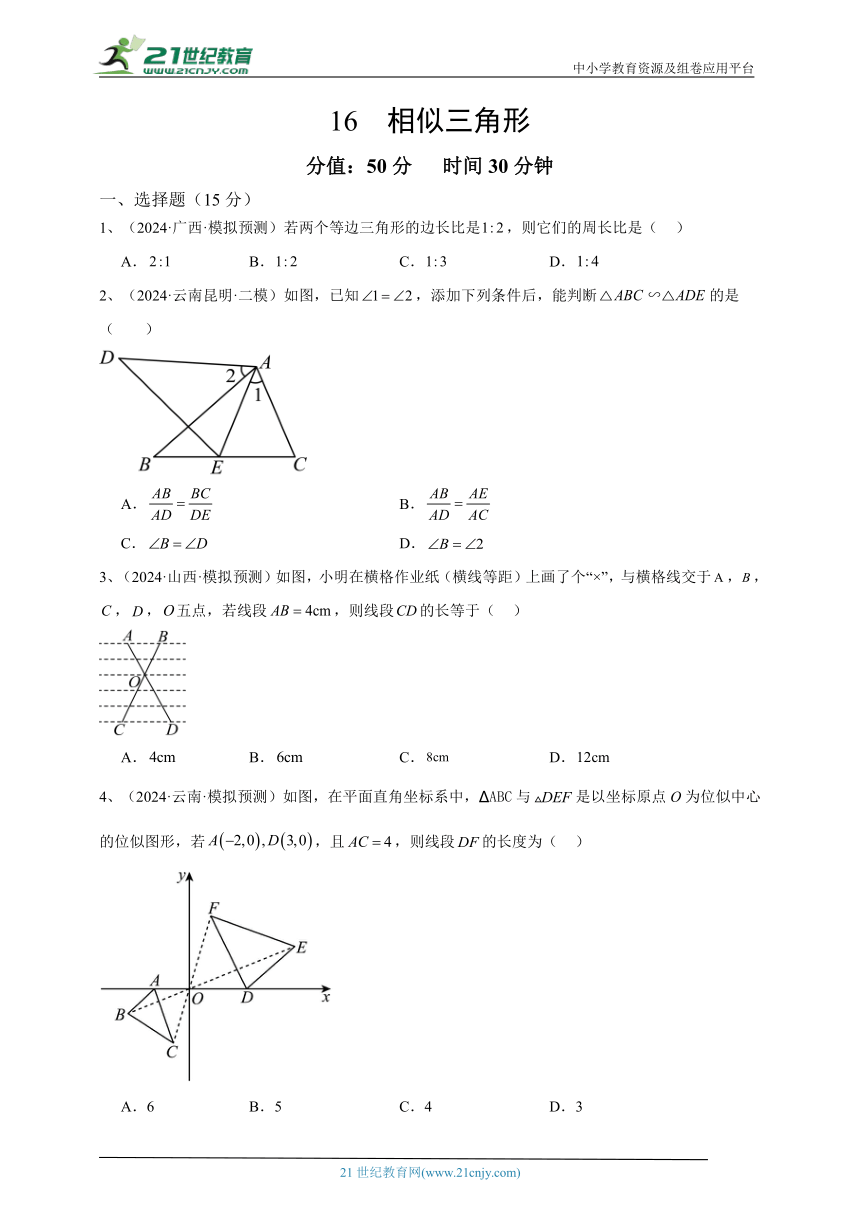 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 15:36:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
16 相似三角形
分值:50分 时间30分钟
选择题(15分)
1、(2024·广西·模拟预测)若两个等边三角形的边长比是,则它们的周长比是( )
A. B. C. D.
2、(2024·云南昆明·二模)如图,已知,添加下列条件后,能判断的是( )
A. B.
C. D.
3、(2024·山西·模拟预测)如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于,,,,五点,若线段,则线段的长等于( )
A. B. C. D.
4、(2024·云南·模拟预测)如图,在平面直角坐标系中, ABC与是以坐标原点O为位似中心的位似图形,若,且,则线段的长度为( )
A.6 B.5 C.4 D.3
5、(2024·广东·模拟预测)如图,在等腰 ABO中,,顶点A为反比例函数(其中)图像上的一点,点B在x轴正半轴上,过点B作,交反比例函数的图像于点C,连接交于点D,若,,则的面积为( )
A. B.6 C. D.5
填空题(15分)
6、(2024·广东·模拟预测)学习相似三角形后,小红利用灯光下自己的影子长度来测量一路灯的高度.如图,已知小红的身高是米,他在路灯下的影长为2米,小红距路灯灯杆的底部4米,则路灯灯泡距地面的高度是 米.
7、(2024·云南·模拟预测)如图,,,则为 .
8、(2024·海南·中考真题)如图是跷跷板示意图,支柱经过的中点O,与地面垂直于点M,,当跷跷板的一端A着地时,另一端B离地面的高度为 .
9、(2024·四川凉山·中考真题)如图,一块面积为的三角形硬纸板(记为 ABC)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是______
10、(2024·湖南·模拟预测)如图,在矩形中,分别是上的点(点分别不与点重合),且,则的最小值为 .
解答题(20分)
11、(2024·广东广州·中考真题)如图,点,分别在正方形的边,上,,,.求证:.
12、(2024·浙江·模拟预测)如图,在正五边形中,连结交于点F
(1)求的度数.
(2)已知,求的长.
13、(2024·广东·模拟预测)九年级(1)班课外活动小组想利用标杆测量佛山千灯湖市民广场醒狮雕塑的高度,见图(醒狮雕塑线条图).已知点A,C,E在同一直线上,标杆高度,标杆与雕塑的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求醒狮雕塑的高度.
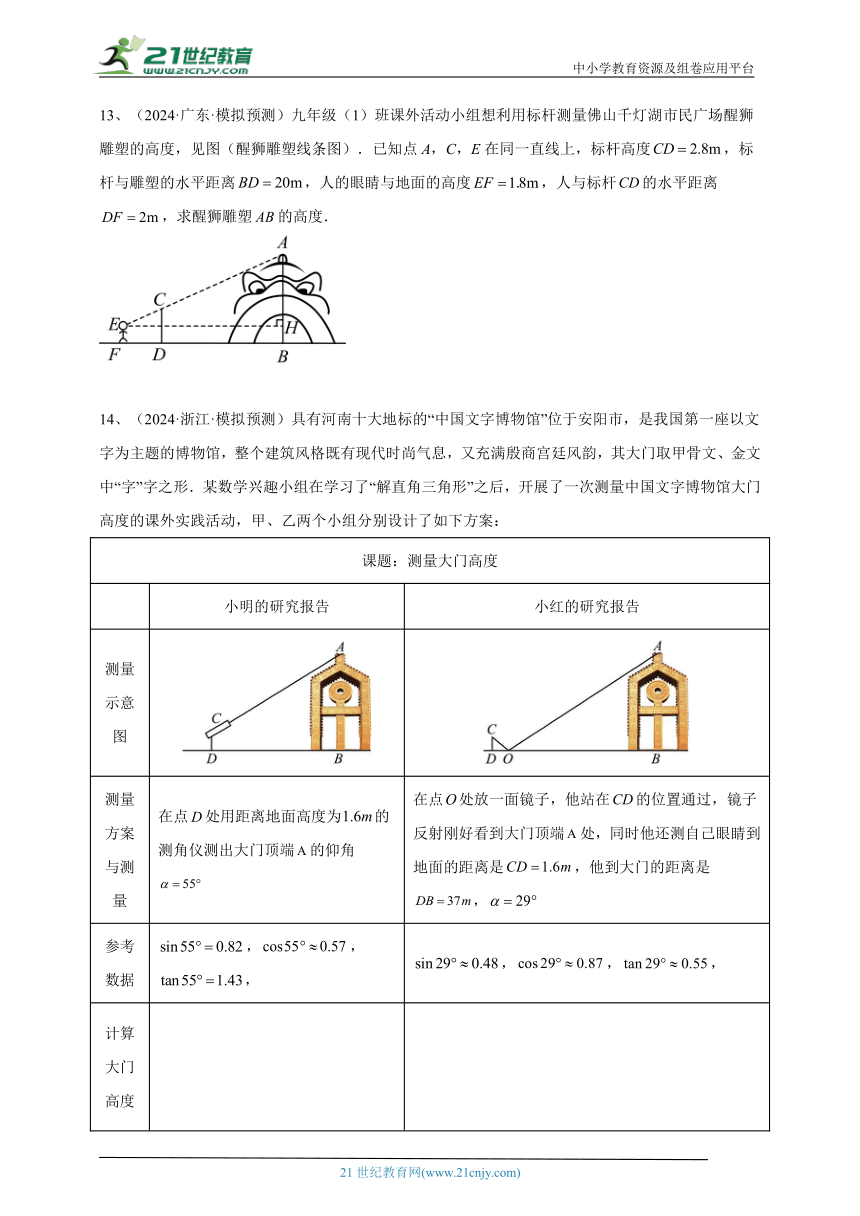
14、(2024·浙江·模拟预测)具有河南十大地标的“中国文字博物馆”位于安阳市,是我国第一座以文字为主题的博物馆,整个建筑风格既有现代时尚气息,又充满殷商宫廷风韵,其大门取甲骨文、金文中“字”字之形.某数学兴趣小组在学习了“解直角三角形”之后,开展了一次测量中国文字博物馆大门高度的课外实践活动,甲、乙两个小组分别设计了如下方案:
课题:测量大门高度
小明的研究报告 小红的研究报告
测量 示意图
测量方案与测量 在点处用距离地面高度为的测角仪测出大门顶端的仰角 在点处放一面镜子,他站在的位置通过,镜子反射刚好看到大门顶端处,同时他还测自己眼睛到地面的距离是,他到大门的距离是,
参考数据 ,,, ,,,
计算大门高度
(1)数学老师看了他们的测量方案后说:“其中一名同学的测量方案存在问题,不能得到测量结果.”你认为 的测量方案存在问题,并提出修改建议.
(2)结合小红的测量方案能计算出中华文字博物馆大门的高度吗?若能,请写出计算过程,并将结果精确到0.1米;若不能,请说明理由.
答案:
一、选择题(15分)
1、(2024·广西·模拟预测)若两个等边三角形的边长比是,则它们的周长比是( )
A. B. C. D.
解:∵两个等边三角形的边长比是,
∴两个三角形三边对应成比例,
∴两个等边三角形相似,
∴它们的周长比是,
故选B.
2、(2024·云南昆明·二模)如图,已知,添加下列条件后,能判断的是( )
A. B.
C. D.
解:∵,
∴,
、添加,不能判定,此选项不符合题意;
、添加,不能判定,此选项不符合题意;
、添加,利用“两角分别对应相等的两个三角形相似”能判定,此选项符合题意;
、添加,不能判定,此选项不符合题意.
故选:C.
3、(2024·山西·模拟预测)如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于,,,,五点,若线段,则线段的长等于( )
A. B. C. D.
解:如图,过点作于点,延长交于点,
∴,
∵作业纸中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
∴,
,
,
∴,即,
解得:,
经检验,是原方程的解且符合题意,
∴
故选:B.
4、(2024·云南·模拟预测)如图,在平面直角坐标系中,与是以坐标原点O为位似中心的位似图形,若,且,则线段的长度为( )
A.6 B.5 C.4 D.3
解:∵与是以坐标原点O为位似中心的位似图形,
∴,且,
∵,
∴,
∴,
∵,
∴;
故选A.
5、(2024·广东·模拟预测)如图,在等腰中,,顶点A为反比例函数(其中)图像上的一点,点B在x轴正半轴上,过点B作,交反比例函数的图像于点C,连接交于点D,若,,则的面积为( )
A. B.6 C. D.5
解:过点A作轴于点H,交于点E,
,
,
,
,
,
,
,
,
,
轴,轴,
,
,
,,
,
,,
设,则,,
,
,
故选:C.
二、填空题(15分)
6、(2024·广东·模拟预测)学习相似三角形后,小红利用灯光下自己的影子长度来测量一路灯的高度.如图,已知小红的身高是米,他在路灯下的影长为2米,小红距路灯灯杆的底部4米,则路灯灯泡距地面的高度是 米.
解:结合题意画出图形得:,,
,
,
小红的身高为米,他在路灯下的影子长为2米;小红距路灯杆底部为4米,
,,,
,
解得:,
则路灯灯泡距地面的高度是米.
故答案为:.
7、(2024·云南·模拟预测)如图,,,则为 .
解:,
,
相似比为,即,
,
;
故答案为:3.
8、(2024·海南·中考真题)如图是跷跷板示意图,支柱经过的中点O,与地面垂直于点M,,当跷跷板的一端A着地时,另一端B离地面的高度为 .
解:过点B作交的延长线于N,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴另一端B离地面的高度为.
故答案为:80.
9、(2024·四川凉山·中考真题)如图,一块面积为的三角形硬纸板(记为)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是______
解:∵一块面积为的三角形硬纸板(记为)平行于投影面时,在点光源的照射下形成的投影是,,
∴,
∴位似图形由三角形硬纸板与其灯光照射下的中心投影组成,相似比为,
∵三角形硬纸板的面积为,
∴,
∴的面积为.
10、(2024·湖南·模拟预测)如图,在矩形中,分别是上的点(点分别不与点重合),且,则的最小值为 .
解:分别以为边作平行四边形,连接,过点E作交于点G,
,
四边形是矩形,
,
矩形中,,
,
,
,,,
,
,
,
,即,
解得:,
四边形是平行四边形,
,
,
,
在中,由勾股定理得:
,
的最小值为,
的最小值为,
故答案为:.
三、解答题(20分)
11、(2024·广东广州·中考真题)如图,点,分别在正方形的边,上,,,.求证:.
解:,,
,
四边形是正方形,
,,
,,
又,
.
12、(2024·浙江·模拟预测)如图,在正五边形中,连结交于点F
(1)求的度数.
(2)已知,求的长.
(1)解:∵五边形是正五边形,
,,
∴,
同理可求,
∴.
(2)解:∵,
∴,
同理可证,
∴四边形是菱形,
,
同理,
∴,
∵,
,
,即,
设,则,
,即,
解得(舍去负值),
的长是.
13、(2024·广东·模拟预测)九年级(1)班课外活动小组想利用标杆测量佛山千灯湖市民广场醒狮雕塑的高度,见图(醒狮雕塑线条图).已知点A,C,E在同一直线上,标杆高度,标杆与雕塑的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求醒狮雕塑的高度.
解:如图所示,设线段与线段交于点G.
∵,
∴,四边形、是矩形,
∴,
∵,
∴,
,
∵,,
∴,,
∴,
∴,
∴
答:醒狮雕塑的高度为.
14、(2024·浙江·模拟预测)具有河南十大地标的“中国文字博物馆”位于安阳市,是我国第一座以文字为主题的博物馆,整个建筑风格既有现代时尚气息,又充满殷商宫廷风韵,其大门取甲骨文、金文中“字”字之形.某数学兴趣小组在学习了“解直角三角形”之后,开展了一次测量中国文字博物馆大门高度的课外实践活动,甲、乙两个小组分别设计了如下方案:
课题:测量大门高度
小明的研究报告 小红的研究报告
测量 示意图
测量方案与测量 在点处用距离地面高度为的测角仪测出大门顶端的仰角 在点处放一面镜子,他站在的位置通过,镜子反射刚好看到大门顶端处,同时他还测自己眼睛到地面的距离是,他到大门的距离是,
参考数据 ,,, ,,,
计算大门高度
(1)数学老师看了他们的测量方案后说:“其中一名同学的测量方案存在问题,不能得到测量结果.”你认为 的测量方案存在问题,并提出修改建议.
(2)结合小红的测量方案能计算出中华文字博物馆大门的高度吗?若能,请写出计算过程,并将结果精确到0.1米;若不能,请说明理由.
【答案】(1)小明
(2)能,理由见详解
【分析】(1)小明测量数据缺少测角仪与大门的距离,由此可判断存在问题的是小明的方案,修改建议只要再测量出测角仪与大门的距离即可;
(2)先利用三角函数关系用表示出和,再利用即可求出大门的高度.
本题是一道综合实践问题,考查解直角三角形仰角俯角问题,解答中涉及相似三角形的判定和性质,理解题意,利用直角三角形的边角关系是解题的关键.
【详解】(1)解: 小明测量数据缺少测角仪与大门的距离,
小明的测量方案存在问题,
修改建议:在方案中加上“测量出测角仪与大门的距离为____m,”即可;
故答案为:小明;
(2)解:能.
作出线段,,
由题意,知,,,
设
在中,
,
,
,
,
,,
,
,
,
,
,,,,
,
解得,
答:中华文字博物馆大门的高度约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
16 相似三角形
分值:50分 时间30分钟
选择题(15分)
1、(2024·广西·模拟预测)若两个等边三角形的边长比是,则它们的周长比是( )
A. B. C. D.
2、(2024·云南昆明·二模)如图,已知,添加下列条件后,能判断的是( )
A. B.
C. D.
3、(2024·山西·模拟预测)如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于,,,,五点,若线段,则线段的长等于( )
A. B. C. D.
4、(2024·云南·模拟预测)如图,在平面直角坐标系中, ABC与是以坐标原点O为位似中心的位似图形,若,且,则线段的长度为( )
A.6 B.5 C.4 D.3
5、(2024·广东·模拟预测)如图,在等腰 ABO中,,顶点A为反比例函数(其中)图像上的一点,点B在x轴正半轴上,过点B作,交反比例函数的图像于点C,连接交于点D,若,,则的面积为( )
A. B.6 C. D.5
填空题(15分)
6、(2024·广东·模拟预测)学习相似三角形后,小红利用灯光下自己的影子长度来测量一路灯的高度.如图,已知小红的身高是米,他在路灯下的影长为2米,小红距路灯灯杆的底部4米,则路灯灯泡距地面的高度是 米.
7、(2024·云南·模拟预测)如图,,,则为 .
8、(2024·海南·中考真题)如图是跷跷板示意图,支柱经过的中点O,与地面垂直于点M,,当跷跷板的一端A着地时,另一端B离地面的高度为 .
9、(2024·四川凉山·中考真题)如图,一块面积为的三角形硬纸板(记为 ABC)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是______
10、(2024·湖南·模拟预测)如图,在矩形中,分别是上的点(点分别不与点重合),且,则的最小值为 .
解答题(20分)
11、(2024·广东广州·中考真题)如图,点,分别在正方形的边,上,,,.求证:.
12、(2024·浙江·模拟预测)如图,在正五边形中,连结交于点F
(1)求的度数.
(2)已知,求的长.
13、(2024·广东·模拟预测)九年级(1)班课外活动小组想利用标杆测量佛山千灯湖市民广场醒狮雕塑的高度,见图(醒狮雕塑线条图).已知点A,C,E在同一直线上,标杆高度,标杆与雕塑的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求醒狮雕塑的高度.
14、(2024·浙江·模拟预测)具有河南十大地标的“中国文字博物馆”位于安阳市,是我国第一座以文字为主题的博物馆,整个建筑风格既有现代时尚气息,又充满殷商宫廷风韵,其大门取甲骨文、金文中“字”字之形.某数学兴趣小组在学习了“解直角三角形”之后,开展了一次测量中国文字博物馆大门高度的课外实践活动,甲、乙两个小组分别设计了如下方案:
课题:测量大门高度
小明的研究报告 小红的研究报告
测量 示意图
测量方案与测量 在点处用距离地面高度为的测角仪测出大门顶端的仰角 在点处放一面镜子,他站在的位置通过,镜子反射刚好看到大门顶端处,同时他还测自己眼睛到地面的距离是,他到大门的距离是,
参考数据 ,,, ,,,
计算大门高度
(1)数学老师看了他们的测量方案后说:“其中一名同学的测量方案存在问题,不能得到测量结果.”你认为 的测量方案存在问题,并提出修改建议.
(2)结合小红的测量方案能计算出中华文字博物馆大门的高度吗?若能,请写出计算过程,并将结果精确到0.1米;若不能,请说明理由.
答案:
一、选择题(15分)
1、(2024·广西·模拟预测)若两个等边三角形的边长比是,则它们的周长比是( )
A. B. C. D.
解:∵两个等边三角形的边长比是,
∴两个三角形三边对应成比例,
∴两个等边三角形相似,
∴它们的周长比是,
故选B.
2、(2024·云南昆明·二模)如图,已知,添加下列条件后,能判断的是( )
A. B.
C. D.
解:∵,
∴,
、添加,不能判定,此选项不符合题意;
、添加,不能判定,此选项不符合题意;
、添加,利用“两角分别对应相等的两个三角形相似”能判定,此选项符合题意;
、添加,不能判定,此选项不符合题意.
故选:C.
3、(2024·山西·模拟预测)如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于,,,,五点,若线段,则线段的长等于( )
A. B. C. D.
解:如图,过点作于点,延长交于点,
∴,
∵作业纸中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
∴,
,
,
∴,即,
解得:,
经检验,是原方程的解且符合题意,
∴
故选:B.
4、(2024·云南·模拟预测)如图,在平面直角坐标系中,与是以坐标原点O为位似中心的位似图形,若,且,则线段的长度为( )
A.6 B.5 C.4 D.3
解:∵与是以坐标原点O为位似中心的位似图形,
∴,且,
∵,
∴,
∴,
∵,
∴;
故选A.
5、(2024·广东·模拟预测)如图,在等腰中,,顶点A为反比例函数(其中)图像上的一点,点B在x轴正半轴上,过点B作,交反比例函数的图像于点C,连接交于点D,若,,则的面积为( )
A. B.6 C. D.5
解:过点A作轴于点H,交于点E,
,
,
,
,
,
,
,
,
,
轴,轴,
,
,
,,
,
,,
设,则,,
,
,
故选:C.
二、填空题(15分)
6、(2024·广东·模拟预测)学习相似三角形后,小红利用灯光下自己的影子长度来测量一路灯的高度.如图,已知小红的身高是米,他在路灯下的影长为2米,小红距路灯灯杆的底部4米,则路灯灯泡距地面的高度是 米.
解:结合题意画出图形得:,,
,
,
小红的身高为米,他在路灯下的影子长为2米;小红距路灯杆底部为4米,
,,,
,
解得:,
则路灯灯泡距地面的高度是米.
故答案为:.
7、(2024·云南·模拟预测)如图,,,则为 .
解:,
,
相似比为,即,
,
;
故答案为:3.
8、(2024·海南·中考真题)如图是跷跷板示意图,支柱经过的中点O,与地面垂直于点M,,当跷跷板的一端A着地时,另一端B离地面的高度为 .
解:过点B作交的延长线于N,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴另一端B离地面的高度为.
故答案为:80.
9、(2024·四川凉山·中考真题)如图,一块面积为的三角形硬纸板(记为)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是______
解:∵一块面积为的三角形硬纸板(记为)平行于投影面时,在点光源的照射下形成的投影是,,
∴,
∴位似图形由三角形硬纸板与其灯光照射下的中心投影组成,相似比为,
∵三角形硬纸板的面积为,
∴,
∴的面积为.
10、(2024·湖南·模拟预测)如图,在矩形中,分别是上的点(点分别不与点重合),且,则的最小值为 .
解:分别以为边作平行四边形,连接,过点E作交于点G,
,
四边形是矩形,
,
矩形中,,
,
,
,,,
,
,
,
,即,
解得:,
四边形是平行四边形,
,
,
,
在中,由勾股定理得:
,
的最小值为,
的最小值为,
故答案为:.
三、解答题(20分)
11、(2024·广东广州·中考真题)如图,点,分别在正方形的边,上,,,.求证:.
解:,,
,
四边形是正方形,
,,
,,
又,
.
12、(2024·浙江·模拟预测)如图,在正五边形中,连结交于点F
(1)求的度数.
(2)已知,求的长.
(1)解:∵五边形是正五边形,
,,
∴,
同理可求,
∴.
(2)解:∵,
∴,
同理可证,
∴四边形是菱形,
,
同理,
∴,
∵,
,
,即,
设,则,
,即,
解得(舍去负值),
的长是.
13、(2024·广东·模拟预测)九年级(1)班课外活动小组想利用标杆测量佛山千灯湖市民广场醒狮雕塑的高度,见图(醒狮雕塑线条图).已知点A,C,E在同一直线上,标杆高度,标杆与雕塑的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求醒狮雕塑的高度.
解:如图所示,设线段与线段交于点G.
∵,
∴,四边形、是矩形,
∴,
∵,
∴,
,
∵,,
∴,,
∴,
∴,
∴
答:醒狮雕塑的高度为.
14、(2024·浙江·模拟预测)具有河南十大地标的“中国文字博物馆”位于安阳市,是我国第一座以文字为主题的博物馆,整个建筑风格既有现代时尚气息,又充满殷商宫廷风韵,其大门取甲骨文、金文中“字”字之形.某数学兴趣小组在学习了“解直角三角形”之后,开展了一次测量中国文字博物馆大门高度的课外实践活动,甲、乙两个小组分别设计了如下方案:
课题:测量大门高度
小明的研究报告 小红的研究报告
测量 示意图
测量方案与测量 在点处用距离地面高度为的测角仪测出大门顶端的仰角 在点处放一面镜子,他站在的位置通过,镜子反射刚好看到大门顶端处,同时他还测自己眼睛到地面的距离是,他到大门的距离是,
参考数据 ,,, ,,,
计算大门高度
(1)数学老师看了他们的测量方案后说:“其中一名同学的测量方案存在问题,不能得到测量结果.”你认为 的测量方案存在问题,并提出修改建议.
(2)结合小红的测量方案能计算出中华文字博物馆大门的高度吗?若能,请写出计算过程,并将结果精确到0.1米;若不能,请说明理由.
【答案】(1)小明
(2)能,理由见详解
【分析】(1)小明测量数据缺少测角仪与大门的距离,由此可判断存在问题的是小明的方案,修改建议只要再测量出测角仪与大门的距离即可;
(2)先利用三角函数关系用表示出和,再利用即可求出大门的高度.
本题是一道综合实践问题,考查解直角三角形仰角俯角问题,解答中涉及相似三角形的判定和性质,理解题意,利用直角三角形的边角关系是解题的关键.
【详解】(1)解: 小明测量数据缺少测角仪与大门的距离,
小明的测量方案存在问题,
修改建议:在方案中加上“测量出测角仪与大门的距离为____m,”即可;
故答案为:小明;
(2)解:能.
作出线段,,
由题意,知,,,
设
在中,
,
,
,
,
,,
,
,
,
,
,,,,
,
解得,
答:中华文字博物馆大门的高度约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
