2025年中考数学一轮复习 17 锐角三角函数与解直角三角形 小测验(含答案)
文档属性
| 名称 | 2025年中考数学一轮复习 17 锐角三角函数与解直角三角形 小测验(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
17 锐角三角函数与解直角三角形
分值:50分 时间30分钟
选择题(15分)
1.(2024·石家庄桥西区模拟)如图,已知在Rt△ABC中,∠B=90°,则cos A= ( )
B. C. D.
2、(2024·唐山丰南区二模)如图,小明在点C处测得树的顶端A仰角为62°,测得BC=10米,则树的高AB(单位:米)为( )
A. B.
C.10tan 62° D.10sin 62°
3、 (2024甘肃临夏)如图,在中,,,则的长是( )
A. 3 B. 6 C. 8 D. 9
4、 (2024四川达州)如图,由8个全等的菱形组成的网格中,每个小菱形的边长均为2,,其中点,,都在格点上,则的值为( )
A. 2 B. C. D. 3
5、(2024安徽省)如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
填空题(15分)
6、(2024·唐山古冶区二模)四边形具有不稳定性.如图,将面积为5的矩形“推”成面积为4的平行四边形,则sin α= ;若α=30°,则平行四边形的面积为 .
7、(2024内蒙古赤峰)综合实践课上,航模小组用无人机测量古树的高度.如图,点C处与古树底部A处在同一水平面上,且米,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为,古树底部A的俯角为,则古树AB的高度约为________米(结果精确到0.1米;参考数据:,,).
8、(2024武汉市)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
9、 (2024江苏盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面的点P处,测得教学楼底端点A的俯角为,再将无人机沿教学楼方向水平飞行至点Q处,测得教学楼顶端点B的俯角为,则教学楼的高度约为________m.(精确到,参考数据:,,)
10、(2024江西省)将图所示的七巧板,拼成图所示的四边形,连接,则______.
解答题(20分)
11、(2024甘肃威武)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒垂直于地面,测角仪,在两侧,,点C与点E相距 (点C,H,E在同一条直线上),在D处测得简尖顶点A的仰角为,在F处测得筒尖顶点A的仰角为.求风电塔筒的高度.(参考数据:,,.)
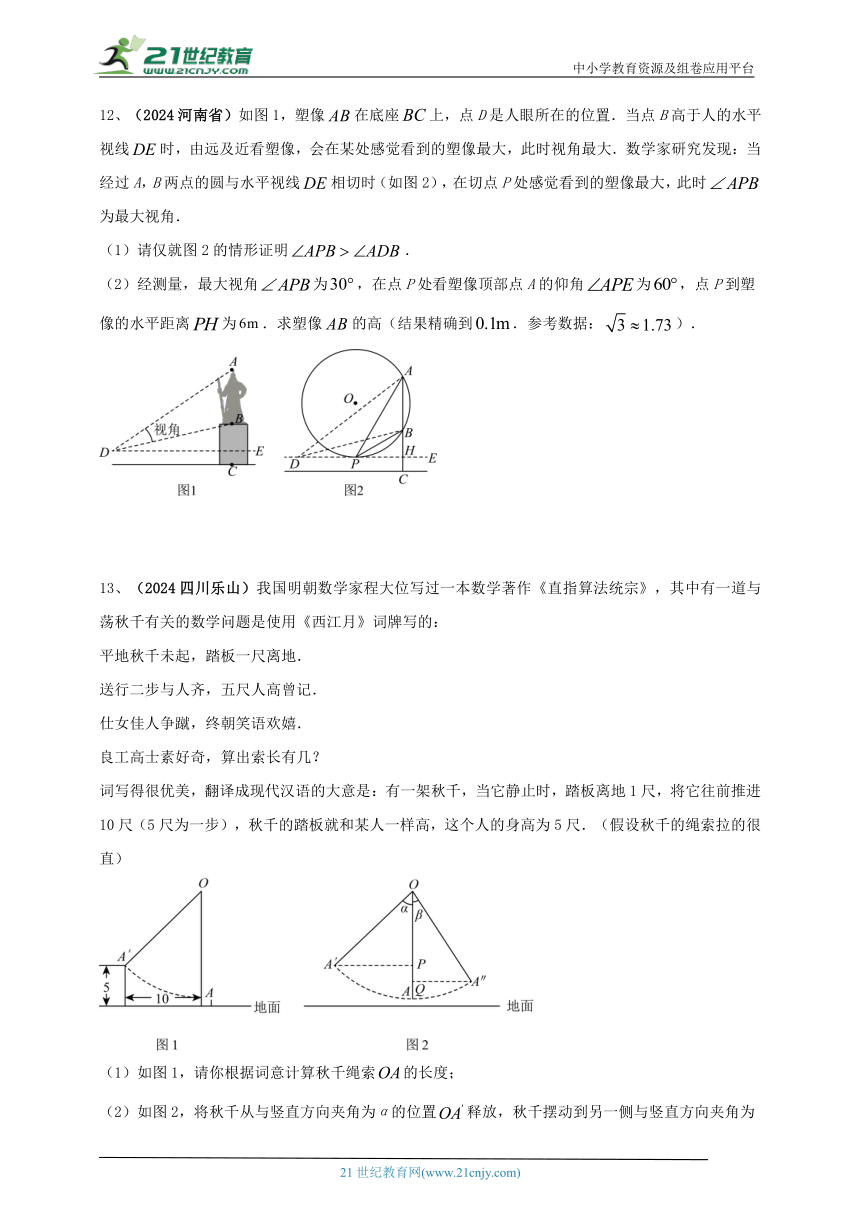
12、(2024河南省)如图1,塑像在底座上,点D是人眼所在的位置.当点B高于人的水平视线时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
(1)请仅就图2的情形证明.
(2)经测量,最大视角为,在点P处看塑像顶部点A的仰角为,点P到塑像的水平距离为.求塑像的高(结果精确到.参考数据:).
13、(2024四川乐山)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图1,请你根据词意计算秋千绳索的长度;
(2)如图2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
14、 (2024天津市)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点依次在同一条水平直线上,,垂足为.在处测得桥塔顶部的仰角()为,测得桥塔底部的俯角()为,又在处测得桥塔顶部的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).参考数据:.
答案
一、选择题(15分)
1.(2024·石家庄桥西区模拟)如图,已知在Rt△ABC中,∠B=90°,则cos A= ( )
B. C. D.
解析:∵∠B=90°,∴cos A=.故选B.
2、(2024·唐山丰南区二模)如图,小明在点C处测得树的顶端A仰角为62°,测得BC=10米,则树的高AB(单位:米)为( )
A. B.
C.10tan 62° D.10sin 62°
解析:由题意得,∠ABC=90°,∠ACB=62°,
在Rt△ABC中,BC=10米,
∴AB=BC·tan 62°=10tan 62°(米).故选C.
3、 (2024甘肃临夏)如图,在中,,,则的长是( )
A. 3 B. 6 C. 8 D. 9
解:如图,过点A作于点D.
∵,
∴.
在中,,
∴,
∴,
∴.
故选B.
4、 (2024四川达州)如图,由8个全等的菱形组成的网格中,每个小菱形的边长均为2,,其中点,,都在格点上,则的值为( )
A. 2 B. C. D. 3
解:如图所示,延长交格点于点,连接,分别在格点上,
依题意,,
∴
∴
又,
∴
∴
故选:B.
5、(2024安徽省)如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
解:过点作的延长线于点,则,
∵,,
∴,,
∴,,
∴为等腰直角三角形,
∴,
设,则,
在中,,
∴,
解得,(舍去),
∴,
∴,
故选:.
二、填空题(15分)
6、(2024·唐山古冶区二模)四边形具有不稳定性.如图,将面积为5的矩形“推”成面积为4的平行四边形,则sin α= ;若α=30°,则平行四边形的面积为 .
解析:如图,过点A作AH⊥BC,垂足为H,
∵AB·BC=5,AH·BC=4,
∴,
∴sin α=,
∵α=30°,
∴sin 30°=,
∴AH=AB,
∴平行四边形的面积为BC·AH=AB·BC=×5=.
7、(2024内蒙古赤峰)综合实践课上,航模小组用无人机测量古树的高度.如图,点C处与古树底部A处在同一水平面上,且米,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为,古树底部A的俯角为,则古树AB的高度约为________米(结果精确到0.1米;参考数据:,,).
解:如图,过点D作,交的延长线于点M,
∴四边形是矩形,
∴米,
∵,,,
∴是等腰直角三角形,
∴米,
在中,(米),
∴(米),
∴古树的高度约为米.
故答案为:.
8、(2024武汉市)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
解:延长交距水平地面的水平线于点D,如图,
由题可知,,
设,
∵
∴
∴
∴
∴
故答案为:51.
9、 (2024江苏盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面的点P处,测得教学楼底端点A的俯角为,再将无人机沿教学楼方向水平飞行至点Q处,测得教学楼顶端点B的俯角为,则教学楼的高度约为________m.(精确到,参考数据:,,)
解:如图,延长交直线于点H,则,
由题意知,
在中,,即,
解得,
,
,,
,
,
,
故答案为:17.
10、(2024江西省)将图所示的七巧板,拼成图所示的四边形,连接,则______.
解:如图,设等腰直角的直角边为,则,小正方形的边长为,
∴,
∴,
∴,
∴,
如图,过点作的延长线于点,则,,
由图()可得,,,
∴,,
∴,
∴,
故答案为:.
三、解答题(20分)
11、(2024甘肃威武)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒垂直于地面,测角仪,在两侧,,点C与点E相距 (点C,H,E在同一条直线上),在D处测得简尖顶点A的仰角为,在F处测得筒尖顶点A的仰角为.求风电塔筒的高度.(参考数据:,,.)
解:如图所示,过点作于G,连接,则四边形是矩形,
∴,,
∵,
∴,
由题意可得,
∴,
∴四边形是矩形,
∴,,
∴,
∴三点共线,
∴;
设,
在中,,
∴
∴;
在中,,
∴
∴;
∴,
解得,
∴,
∴,
∴风电塔筒的高度约为.
12、(2024河南省)如图1,塑像在底座上,点D是人眼所在的位置.当点B高于人的水平视线时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
(1)请仅就图2的情形证明.
(2)经测量,最大视角为,在点P处看塑像顶部点A的仰角为,点P到塑像的水平距离为.求塑像的高(结果精确到.参考数据:).
证明:如图,连接.
则.
∵,
∴.
【小问2详解】
解:在中,,.
∵,
∴.
∵,
∴.
在中,,
∴.
∴.
答:塑像的高约为.
13、(2024四川乐山)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图1,请你根据词意计算秋千绳索的长度;
(2)如图2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
解:如图,过点作,垂足为点B.
设秋千绳索的长度为x尺.
由题可知,,,,
∴.
在中,由勾股定理得:
∴.
解得.
答:秋千绳索的长度为尺.
【小问2详解】
能.
由题可知,,.
在中,,
同理,.
∵,
∴.
∴.
14、 (2024天津市)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点依次在同一条水平直线上,,垂足为.在处测得桥塔顶部的仰角()为,测得桥塔底部的俯角()为,又在处测得桥塔顶部的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).参考数据:.
解:设,由,得.
,垂足为,
.
在中,,
.
在中,,
.
.
得.
答:线段的长约为.
【小问2详解】
在中,,
.
.
答:桥塔的高度约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
17 锐角三角函数与解直角三角形
分值:50分 时间30分钟
选择题(15分)
1.(2024·石家庄桥西区模拟)如图,已知在Rt△ABC中,∠B=90°,则cos A= ( )
B. C. D.
2、(2024·唐山丰南区二模)如图,小明在点C处测得树的顶端A仰角为62°,测得BC=10米,则树的高AB(单位:米)为( )
A. B.
C.10tan 62° D.10sin 62°
3、 (2024甘肃临夏)如图,在中,,,则的长是( )
A. 3 B. 6 C. 8 D. 9
4、 (2024四川达州)如图,由8个全等的菱形组成的网格中,每个小菱形的边长均为2,,其中点,,都在格点上,则的值为( )
A. 2 B. C. D. 3
5、(2024安徽省)如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
填空题(15分)
6、(2024·唐山古冶区二模)四边形具有不稳定性.如图,将面积为5的矩形“推”成面积为4的平行四边形,则sin α= ;若α=30°,则平行四边形的面积为 .
7、(2024内蒙古赤峰)综合实践课上,航模小组用无人机测量古树的高度.如图,点C处与古树底部A处在同一水平面上,且米,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为,古树底部A的俯角为,则古树AB的高度约为________米(结果精确到0.1米;参考数据:,,).
8、(2024武汉市)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
9、 (2024江苏盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面的点P处,测得教学楼底端点A的俯角为,再将无人机沿教学楼方向水平飞行至点Q处,测得教学楼顶端点B的俯角为,则教学楼的高度约为________m.(精确到,参考数据:,,)
10、(2024江西省)将图所示的七巧板,拼成图所示的四边形,连接,则______.
解答题(20分)
11、(2024甘肃威武)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒垂直于地面,测角仪,在两侧,,点C与点E相距 (点C,H,E在同一条直线上),在D处测得简尖顶点A的仰角为,在F处测得筒尖顶点A的仰角为.求风电塔筒的高度.(参考数据:,,.)
12、(2024河南省)如图1,塑像在底座上,点D是人眼所在的位置.当点B高于人的水平视线时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
(1)请仅就图2的情形证明.
(2)经测量,最大视角为,在点P处看塑像顶部点A的仰角为,点P到塑像的水平距离为.求塑像的高(结果精确到.参考数据:).
13、(2024四川乐山)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图1,请你根据词意计算秋千绳索的长度;
(2)如图2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
14、 (2024天津市)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点依次在同一条水平直线上,,垂足为.在处测得桥塔顶部的仰角()为,测得桥塔底部的俯角()为,又在处测得桥塔顶部的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).参考数据:.
答案
一、选择题(15分)
1.(2024·石家庄桥西区模拟)如图,已知在Rt△ABC中,∠B=90°,则cos A= ( )
B. C. D.
解析:∵∠B=90°,∴cos A=.故选B.
2、(2024·唐山丰南区二模)如图,小明在点C处测得树的顶端A仰角为62°,测得BC=10米,则树的高AB(单位:米)为( )
A. B.
C.10tan 62° D.10sin 62°
解析:由题意得,∠ABC=90°,∠ACB=62°,
在Rt△ABC中,BC=10米,
∴AB=BC·tan 62°=10tan 62°(米).故选C.
3、 (2024甘肃临夏)如图,在中,,,则的长是( )
A. 3 B. 6 C. 8 D. 9
解:如图,过点A作于点D.
∵,
∴.
在中,,
∴,
∴,
∴.
故选B.
4、 (2024四川达州)如图,由8个全等的菱形组成的网格中,每个小菱形的边长均为2,,其中点,,都在格点上,则的值为( )
A. 2 B. C. D. 3
解:如图所示,延长交格点于点,连接,分别在格点上,
依题意,,
∴
∴
又,
∴
∴
故选:B.
5、(2024安徽省)如图,在中,,点在的延长线上,且,则的长是( )
A. B. C. D.
解:过点作的延长线于点,则,
∵,,
∴,,
∴,,
∴为等腰直角三角形,
∴,
设,则,
在中,,
∴,
解得,(舍去),
∴,
∴,
故选:.
二、填空题(15分)
6、(2024·唐山古冶区二模)四边形具有不稳定性.如图,将面积为5的矩形“推”成面积为4的平行四边形,则sin α= ;若α=30°,则平行四边形的面积为 .
解析:如图,过点A作AH⊥BC,垂足为H,
∵AB·BC=5,AH·BC=4,
∴,
∴sin α=,
∵α=30°,
∴sin 30°=,
∴AH=AB,
∴平行四边形的面积为BC·AH=AB·BC=×5=.
7、(2024内蒙古赤峰)综合实践课上,航模小组用无人机测量古树的高度.如图,点C处与古树底部A处在同一水平面上,且米,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为,古树底部A的俯角为,则古树AB的高度约为________米(结果精确到0.1米;参考数据:,,).
解:如图,过点D作,交的延长线于点M,
∴四边形是矩形,
∴米,
∵,,,
∴是等腰直角三角形,
∴米,
在中,(米),
∴(米),
∴古树的高度约为米.
故答案为:.
8、(2024武汉市)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
解:延长交距水平地面的水平线于点D,如图,
由题可知,,
设,
∵
∴
∴
∴
∴
故答案为:51.
9、 (2024江苏盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面的点P处,测得教学楼底端点A的俯角为,再将无人机沿教学楼方向水平飞行至点Q处,测得教学楼顶端点B的俯角为,则教学楼的高度约为________m.(精确到,参考数据:,,)
解:如图,延长交直线于点H,则,
由题意知,
在中,,即,
解得,
,
,,
,
,
,
故答案为:17.
10、(2024江西省)将图所示的七巧板,拼成图所示的四边形,连接,则______.
解:如图,设等腰直角的直角边为,则,小正方形的边长为,
∴,
∴,
∴,
∴,
如图,过点作的延长线于点,则,,
由图()可得,,,
∴,,
∴,
∴,
故答案为:.
三、解答题(20分)
11、(2024甘肃威武)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒垂直于地面,测角仪,在两侧,,点C与点E相距 (点C,H,E在同一条直线上),在D处测得简尖顶点A的仰角为,在F处测得筒尖顶点A的仰角为.求风电塔筒的高度.(参考数据:,,.)
解:如图所示,过点作于G,连接,则四边形是矩形,
∴,,
∵,
∴,
由题意可得,
∴,
∴四边形是矩形,
∴,,
∴,
∴三点共线,
∴;
设,
在中,,
∴
∴;
在中,,
∴
∴;
∴,
解得,
∴,
∴,
∴风电塔筒的高度约为.
12、(2024河南省)如图1,塑像在底座上,点D是人眼所在的位置.当点B高于人的水平视线时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B两点的圆与水平视线相切时(如图2),在切点P处感觉看到的塑像最大,此时为最大视角.
(1)请仅就图2的情形证明.
(2)经测量,最大视角为,在点P处看塑像顶部点A的仰角为,点P到塑像的水平距离为.求塑像的高(结果精确到.参考数据:).
证明:如图,连接.
则.
∵,
∴.
【小问2详解】
解:在中,,.
∵,
∴.
∵,
∴.
在中,,
∴.
∴.
答:塑像的高约为.
13、(2024四川乐山)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图1,请你根据词意计算秋千绳索的长度;
(2)如图2,将秋千从与竖直方向夹角为α的位置释放,秋千摆动到另一侧与竖直方向夹角为β的地方,两次位置的高度差.根据上述条件能否求出秋千绳索的长度?如果能,请用含α、β和h的式子表示;如果不能,请说明理由.
解:如图,过点作,垂足为点B.
设秋千绳索的长度为x尺.
由题可知,,,,
∴.
在中,由勾股定理得:
∴.
解得.
答:秋千绳索的长度为尺.
【小问2详解】
能.
由题可知,,.
在中,,
同理,.
∵,
∴.
∴.
14、 (2024天津市)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点依次在同一条水平直线上,,垂足为.在处测得桥塔顶部的仰角()为,测得桥塔底部的俯角()为,又在处测得桥塔顶部的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).参考数据:.
解:设,由,得.
,垂足为,
.
在中,,
.
在中,,
.
.
得.
答:线段的长约为.
【小问2详解】
在中,,
.
.
答:桥塔的高度约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
