小升初解决问题专题01:分数应用题-2024-2025学年数学六年级下册苏教版(含解析)
文档属性
| 名称 | 小升初解决问题专题01:分数应用题-2024-2025学年数学六年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 517.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 17:03:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初解决问题专题01:分数应用题
1.希望小学有男生560人,女生人数是男生人数的,男生比女生少多少人?
2.一项工程甲单独做15天完成,乙单独做12天完成,现他们合做若干天后,剩下的由乙单独做3天才能完成,甲、乙合做了多少天?
3.我国人均水资源只有2300立方米,仅为世界平均水平的,是全球人均水资源最贫乏的国家之一。据统计,我国660个城市中,有30%的城市供水不足,在这些供水不足的城市中,又有的城市严重缺水。这些城市中,严重缺水的城市有多少个?
4.朝阳农场收获一批蔬菜,如果用小汽车运输,12次才能运完;如果用大卡车运输,需要运6次;如果两辆车一起运,多少次才能运完?
5.某厂第一车间的人数比第二车间人数的少30人,如果从第二车间调10人到第一车间,这时第一车间的人数是第二车间人数的。原来两个车间各有多少人?
6.一项工程,甲单独做10天完成,乙单独做15天完成,两人合作需要多少天完成这项工程的?
7.六(1)班原来女生占全班人数的。新学期转出了4名女生,这时女生占全班人数的。六(1)班现在有女生多少人?
8.果果和妈妈一起去超市,买洗漱用品花了总钱数的少100元,买小食品花了余下的多20元,又买了一个580元的饮水机,正好花完所带的钱,果果妈妈一共带了多少钱?
9.青山饲养场今年养鸡和鸭共6300只,其中鸡的只数是鸭的,青山饲养场今年养鸡和鸭各多少只?
10.儿童的负重最好不要超过本人体重的,如果长期背负过重物体,会导致腰痛、背痛,严重的甚至会妨碍骨骼生长。你觉得王明的书包超重吗?为什么?
11.“中国天眼”超越著名的美国天文望远镜阿雷西博,成为全球最大且最灵敏的射电望远镜,这意味着人类向宇宙未知地带探索的眼力更加深邃,眼界更加开阔。阿雷西博天文望远镜的直径为350米,比“中国天眼”的直径短,你能求出“中国天眼”的直径吗?
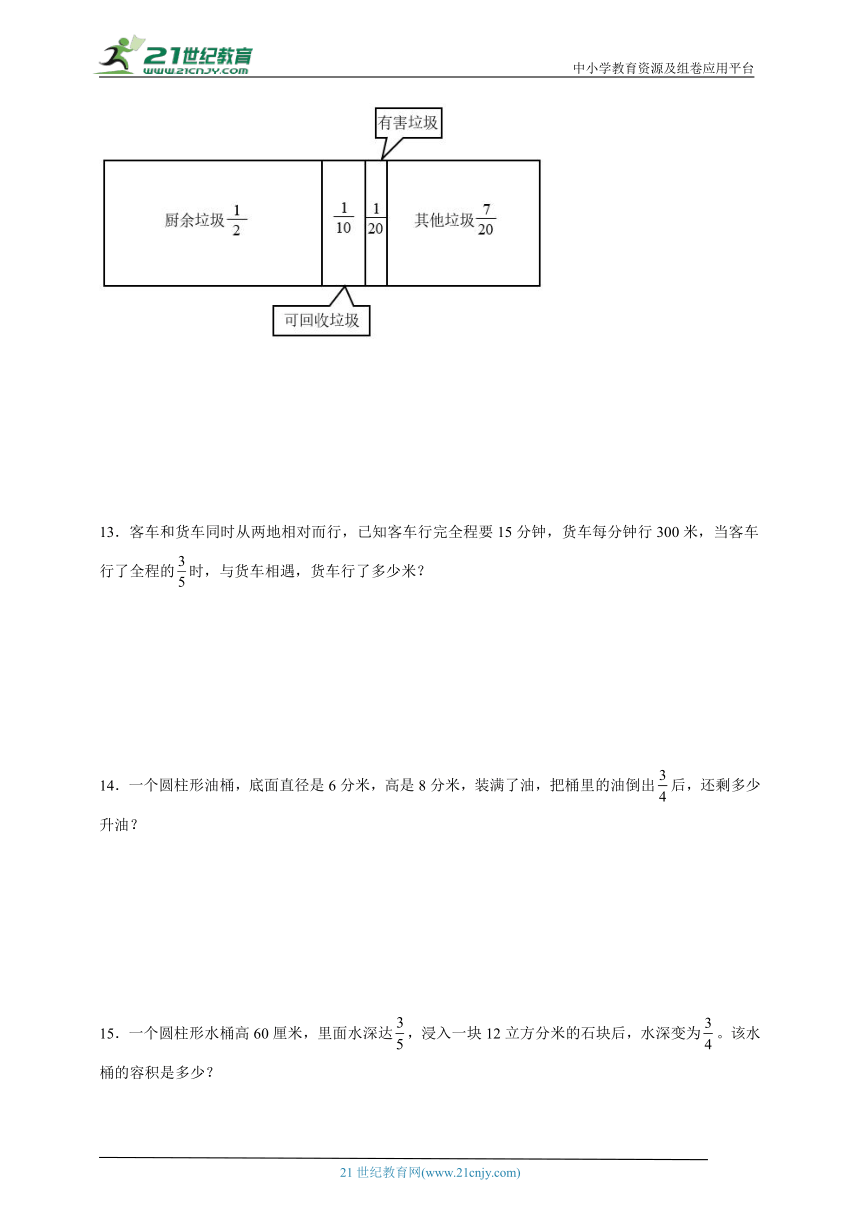
12.按照《北京市生活垃圾条例》规定,生活垃圾按厨余垃圾、有害垃圾、可回收物、其他垃圾分为四类。如图是某小区对产生的生活垃圾做的一项统计。这个小区产生的厨余垃圾、可回收物和其他垃圾一共占生活垃圾的几分之几?
13.客车和货车同时从两地相对而行,已知客车行完全程要15分钟,货车每分钟行300米,当客车行了全程的时,与货车相遇,货车行了多少米?
14.一个圆柱形油桶,底面直径是6分米,高是8分米,装满了油,把桶里的油倒出后,还剩多少升油?
15.一个圆柱形水桶高60厘米,里面水深达,浸入一块12立方分米的石块后,水深变为。该水桶的容积是多少?
16.解放路小学六年级有学生306人,选出男生的和12名女生参加区上组织的“六一”儿童节文艺汇演,选好后剩下的男、女生人数恰巧一样多。解放路小学六年级男、女生各多少人?
17.有一个圆锥形容器,它的底面直径是2分米,高是15厘米,把它装满水后,全部倒入从里面量长是12厘米、宽是10厘米的长方体水槽中,水面的高度正好是水槽高的,这个水槽的高是多少厘米?(得数精确到十分位)
18.东风机械厂有两个车间,甲车间人数是乙车间人数的,如果从乙车间调18人到甲车间,则两个车间人数相等,甲、乙两个车间原来各有多少人?
19.为响应“绿水青山就是金山银山”号召,学校组织五、六年级积极开展植树活动。两个年级共植树96棵,其中五年级植树棵数是六年级的。五、六年级各植树多少棵?
20.甲、乙两个工程队合修一条水渠,甲工程队先修了4500米后,乙工程队修了剩下的,还剩2000米。这条水渠长多少米?
21.每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。笑笑家为了节约用水,做了一个无盖圆柱形铁皮水桶蓄水,高10分米,底面直径是高的,做这个水桶至少要用多少平方分米的铁皮?
22.为保障疫情期间的医疗物资供应,全国各地医疗物资生产企业加班加点生产,某企业接到生产一批防护服的任务,第一天生产的套数与总套数的比是1∶5,第二天生产了660套防护服,两天完成的套数比未完成的套数少。这批防护服的生产任务共是多少套?
23.一批水果,卖出这批水果的,这时剩下的比卖出的多150千克。这批水果原来一共多少千克?
24.习爷爷提出“绿水青山就是金山银山”。科研人员在西北某沙漠的一个区域种植胡杨800棵,种植沙柳的是胡杨棵数的,又是沙枣棵数的,这个区域种植沙枣树多少棵?
1.70人
【分析】把男生人数看作单位“1”,女生人数是男生人数的,用乘法计算。得出女生人数,再减男生人数即可。
【详解】
(人)
答:男生比女生少70人。
2.5天
【分析】将这项工程的工作量当作单位“1”,则甲、乙的工作效率分别、,则乙单独做3天能完成总工作量×3=,其余的1-由他们合做完成,则根据工作量÷工作效率=工作时间可知,甲、乙合做的天数为(1-)÷()。
【详解】(1-×3)÷()
=(1-×3)÷()
=(1-×3)÷
=(1-)÷
=÷
=×
=
=5(天)
答:甲、乙合做了5天。
3.66个
【分析】用我们城市总个数乘30%,得出供水不足的城市个数,再乘,即为严重缺水的城市有多少个,据此解答。
【详解】
(个)
答:这些城市中,严重缺水的城市有66个。
【点睛】解答本题的关键是要掌握已知一个数,求它的几分之几是多少,用乘法计算;求一个数的百分之几是多少,用乘法计算。
4.4次
【分析】把这批蔬菜看作单位“1”,根据工作总量÷工作时间=工作效率,据此分别求出小汽车的工作效率为,大卡车的工作效率为,再根据工作总量÷工作效率之和=工作时间,据此进行计算即可。
【详解】1÷(+)
=1÷
=4(次)
答:如果两辆车一起运,4次才能运完。
【点睛】本题考查工程问题,明确工作总量、工作时间和工作效率之间的关系是解题的关键。
5.原来第一车间有170人,第二车间有250人
【分析】根据“第一车间的人数比第二车间人数的少30人”,可知第二车间人数第一车间人数;又“从第二车间调10人到第一车间,这时第一车间的人数是第二车间人数的”,可知第一车间人数(第二车间人数;据此可设原来第二车间有人,那么第一车间就有人;进而列方程得解。
【详解】解:设原来第二车间有人,那么第一车间就有人。
第一车间有:(人)。
答:原来第一车间有170人,第二车间有250人。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可。
6.4天
【分析】将工作总量看作单位“1”,时间分之一可以看作效率,这项工程的÷两队效率和=合作天数,据此列式解答。
【详解】÷(+)
=÷
=×6
=4(天)
答:两人合作需要4天完成这项工程的。
【点睛】关键是理解工作效率、工作时间、工作总量之间的关系。
7.20人
【分析】由题意可知,将不变量看作单位“1”,男生人数不变,所以将男生人数看作单位“1”,则原来的女生人数占男生人数的,现在的女生人数占男生人数的,根据部分的量÷所对应的分率=单位“1”的量,求出男生人数,再进一步求出女生人数即可。
【详解】4÷(-)
=4÷(-)
=4÷
=30(人)
30×=30×=20(人)
答:六(1)班现在有女生20人。
【点睛】本题考查分数除法,明确将不变的量看作单位“1”是解题的关键。
8.1000元
【分析】先把用完总钱数的后剩下的钱数看作单位“1”,饮水机的钱数加上多出的20元刚好占单位“1”的(1-),根据“量÷对应的分率”求出用完总钱数的后剩下的钱数,再把妈妈一共带的钱数看作单位“1”,从剩下的钱数里面拿出100元给洗漱用品花的钱数,则(900-100)元占全部钱数的(1-),根据“量÷对应的分率”求出妈妈带的总钱数,据此解答。
【详解】
(580+20)÷(1-)
=600÷
=900(元)
(900-100)÷(1-)
=800÷
=1000(元)
答:果果妈妈一共带了1000元钱。
【点睛】本题属于比较复杂的分数除法应用题,两个分数的单位“1”不相同,找出量和对应的分率是解答题目的关键。
9.鸡:2800只;鸭:3500只
【分析】将鸭子的数量看成单位“1”,鸡的只数是鸭的,则6300只对应鸭子的数量的(1+)=,根据分数除法的意义,用6300÷即可求出鸭子的数量;再用总数量减去鸭子的数量,即可求出鸡的数量,据此解答。
【详解】6300÷(1+)
=6300÷
=3500(只)
6300-3500=2800(只)
答:青山饲养场今年养鸡2800只,养鸭3500只。
【点睛】此题考查了分数除法的应用,找出与已知量对应的分率是解答此类问题的关键。
10.超重;不超重的书包质量为4.5千克,王明的书包质量超过了4.5千克,所以书包超重。
【分析】先用分数乘法求出王明体重的,再和书包的质量比较大小,如果结果大于5千克,书包不超重,如果结果小于5千克,书包超重,据此解答。
【详解】30×=4.5(千克)
因为5千克>4.5千克,所以书包超重。
答:书包超重,因为不超重的书包质量为4.5千克,王明的书包质量超过了4.5千克,所以书包超重。
【点睛】已知一个数,求这个数的几分之几是多少用分数乘法计算。
11.500米
【分析】根据题意,阿雷西博天文望远镜的直径比“中国天眼”的直径短,把“中国天眼”的直径看作单位“1”,阿雷西博天文望远镜的直径是“中国天眼”的直径的(1-),单位“1”未知,用阿雷西博天文望远镜的直径除以(1-),即可求出“中国天眼”的直径。
【详解】350÷(1-)
=350÷
=350×
=500(米)
答:“中国天眼”的直径是500米。
【点睛】本题考查分数除法的意义及应用,明确已知比一个数多或少几分之几是多少,求这个数,用除法计算。
12.
【分析】把生活垃圾看作单位“1”,根据加法的意义,用加法求出厨余垃圾、可回收物、其他垃圾占生活垃圾的分率之和即可。
【详解】
答:这个小区产生的厨余垃圾、可回收物和其他垃圾一共占生活垃圾的。
【点睛】本题考查分数加法的应用,掌握异分母分数加法的计算法则是解题的关键。
13.2700米
【分析】由题意可知,两车相遇时,客车和货车行驶的时间是一样的,然后把两地的距离看作单位“1”,根据路程÷时间=速度,据此可求出客车的速度是,然后再根据路程÷速度=时间,据此求出客车行驶的时间,最后根据速度×时间=路程,据此出货车行驶的距离。
【详解】÷=9(分钟)
300×9=2700(米)
答:与货车相遇,货车行了2700米。
【点睛】本题考查路程、时间和速度之间的关系,明确两车相遇时,客车和货车行驶的时间是一样的是解题的关键。
14.56.52升
【分析】根据圆柱的体积公式:底面积×高,把数代入即可求出圆柱形油桶的体积,再根据1立方分米=1升,转换单位,由于倒出桶里的后,单位“1”是桶里的量,单位“1”已知,用乘法,用桶里的量×,之后再用桶里的量减去用掉的即可求出剩下的。
【详解】3.14×(6÷2)2×8
=3.14×9×8
=226.08(立方分米)
226.08立方分米=226.08升
226.08×=169.56(升)
226.08-169.56=56.52(升)
答:还剩56.52升。
【点睛】本题主要考查圆柱的体积公式,熟练掌握它的体积公式并灵活运用,同时要注意体积和容积的换算。
15.80立方分米
【分析】根据圆柱的体积(容积)公式V=Sh,水桶的底面积不变,所以高的比等于体积的比,把水桶的高看作单位“1”,原来的水深占水桶高的,浸入一块12立方分米的石块后,水深变为。据此可以求出水面上升的高占水桶高的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】12÷(-)
=12÷
=80(立方分米)
答:该水桶的容积是80立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
16.男生:154人;女生:152人
【分析】设男生有x人,则女生有(306-x)人,选出男生的是x人,剩下的男生有(x-x)人,选出12名女生,女生还剩(306-x-12)人,剩下的男生和女生人数一样,列方程:x-x=306-x-12,解方程,即可解答。
【详解】解:设男生有x人,女生有(306-x)人。
x-x=306-x-12
x+x=294
x=294
x=294÷
x=294×
x=154
女生有:306-154=152(人)
答:解放路小学六年级男生有154人,女生有152人。
【点睛】根据方程的实际应用,利用男生人数、女生人数和总人数之间的关系,设出未知数,找出相关的量,列方程,解方程。
17.26.2厘米
【分析】根据圆锥的体积公式:V=Sh,据此求出水的体积,然后根据长方体的体积公式:V=abh,据此求出水面的高度,水面的高度正好是水槽高的,根据除法的意义,用除法解答即可。
【详解】2分米=20厘米
×3.14×(20÷2)2×15÷(12×10)÷
=×3.14×100×15÷120÷
=1570÷120÷
=1570÷(120×)
=1570÷60
≈26.2(厘米)
答:这个水槽的高是26.2厘米。
【点睛】本题考查圆锥和长方体的体积,熟记公式是解题的关键。
18.甲车间原来有60人,乙车间原来有96人
【分析】把乙车间原来的人数看作单位“1”,由题意可知,乙车间比甲车间多2个18人,即(18×2)人,这(18×2)人正好是乙车间人数的(1-),根据分数除法的意义,用(18×2)人除以(1-),就是乙车间原来的人数。再根据分数乘法的意义,用乙车间原来的人数乘,就是甲车间原来的人数。
【详解】18×2÷(1-)
=36÷
=96(人)
96×=60(人)
答:甲车间原来有60人,乙车间原来有96人。
【点睛】此题是考查分数乘、除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
19.40棵;56棵
【分析】把六年级植树棵数看作单位“1”,则五年级植树棵数是,两个年级植树棵数是(1+),根据分数除法的意义,用两个年级共植树棵数除以(1+),就是六年级植树棵数;再根据分数乘法的意义,用六年级植树棵数乘,就是五年级植树棵数。
【详解】96÷(1+)
=96÷
=56(棵)
56×=40(棵)
答:五年级植树40棵,六年级植树56棵。
【点睛】此题是考查分数乘、除法的意义及应用。求一个数的几分之几是多少,用这个数乘分率;已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率。
20.11500米
【分析】把甲工程队先修后剩下的长度看作单位“1”,甲工程队先修了4500米后,乙工程队修了剩下的,还剩2000米,那么可知2000米占甲工程队先修后剩下的长度的(1-),用除法计算即可求出甲工程队先修后剩下的长度,然后再加上甲工程队先修的4500米,即可求出这条水渠长多少米。
【详解】2000÷(1-)+4500
=2000÷+4500
=7000+4500
=11500(米)
答:这条水渠长11500米。
【点睛】本题关键是把甲工程队先修后剩下的长度看作单位“1”,求出甲工程队先修后剩下的长度是解题的关键。
21.138.16平方分米
【分析】因为底面直径是高的,高是8分米,所以底面直径为:10×=4(分米)。因为是无盖水桶,所以它的表面积等于圆柱的侧面积加上底面积即可。
【详解】10×=4(分米)
3.14×4×10+3.14×(4÷2)2
=125.6+12.56
=138.16(平方分米)
答:这个水桶至少要用铁皮138.16平方分米。
【点睛】本题的解答关键在于先求出底面直径,再根据圆柱的表面积公式即可解答。
22.2700套
【分析】设这批防护服的生产任务一共是x套,第一天生产的套数与总套数的比是1∶5,第一天生产x(套),根据等量关系:两天完成的套数=未完成的套数×(1-),列方程解答即可。
【详解】解:设这批防护服的生产任务一共是x套。
x+660=(x-x-660)×(1-)
x+660=(x-660)×
x+660=x-528
x=1188
x=2700
答:这批防护服的生产任务一共是2700套。
【点睛】本题主要考查了比及分数的应用,关键是根据等量关系:两天完成的套数=未完成的套数×(1-),列方程。
23.750千克
【分析】把这批水果的千克数看作单位“1”,卖出这批水果的,剩下这批水果的(1-),由此可知150千克相当于这批水果的(1--),根据已知一个数的几分之几是多少,求这个数,用除法求出这批水果的千克数即可。
【详解】150÷(1--)
=150÷
=750(千克)
答:这批水果原来一共750千克。
【点睛】此题属于基本的分数四则复合应用题,解题的关键是正确找出单位“1”和150千克对应的分率。
24.600棵
【分析】把胡杨的棵数看作单位“1”,单位“1”已知,根据分数乘法的意义,用800乘求出沙柳的棵数,接着把沙枣的棵数看作单位“1”,单位“1”未知,根据分数除法的意义,用沙柳的棵数除以,即可求出沙枣树的棵数。
【详解】800×÷
=500÷
=600(棵)
答:这个区域种植沙枣树600棵。
【点睛】此题主要考查分数乘除法的意义,注意前后两个单位“1”的不同。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初解决问题专题01:分数应用题
1.希望小学有男生560人,女生人数是男生人数的,男生比女生少多少人?
2.一项工程甲单独做15天完成,乙单独做12天完成,现他们合做若干天后,剩下的由乙单独做3天才能完成,甲、乙合做了多少天?
3.我国人均水资源只有2300立方米,仅为世界平均水平的,是全球人均水资源最贫乏的国家之一。据统计,我国660个城市中,有30%的城市供水不足,在这些供水不足的城市中,又有的城市严重缺水。这些城市中,严重缺水的城市有多少个?
4.朝阳农场收获一批蔬菜,如果用小汽车运输,12次才能运完;如果用大卡车运输,需要运6次;如果两辆车一起运,多少次才能运完?
5.某厂第一车间的人数比第二车间人数的少30人,如果从第二车间调10人到第一车间,这时第一车间的人数是第二车间人数的。原来两个车间各有多少人?
6.一项工程,甲单独做10天完成,乙单独做15天完成,两人合作需要多少天完成这项工程的?
7.六(1)班原来女生占全班人数的。新学期转出了4名女生,这时女生占全班人数的。六(1)班现在有女生多少人?
8.果果和妈妈一起去超市,买洗漱用品花了总钱数的少100元,买小食品花了余下的多20元,又买了一个580元的饮水机,正好花完所带的钱,果果妈妈一共带了多少钱?
9.青山饲养场今年养鸡和鸭共6300只,其中鸡的只数是鸭的,青山饲养场今年养鸡和鸭各多少只?
10.儿童的负重最好不要超过本人体重的,如果长期背负过重物体,会导致腰痛、背痛,严重的甚至会妨碍骨骼生长。你觉得王明的书包超重吗?为什么?
11.“中国天眼”超越著名的美国天文望远镜阿雷西博,成为全球最大且最灵敏的射电望远镜,这意味着人类向宇宙未知地带探索的眼力更加深邃,眼界更加开阔。阿雷西博天文望远镜的直径为350米,比“中国天眼”的直径短,你能求出“中国天眼”的直径吗?
12.按照《北京市生活垃圾条例》规定,生活垃圾按厨余垃圾、有害垃圾、可回收物、其他垃圾分为四类。如图是某小区对产生的生活垃圾做的一项统计。这个小区产生的厨余垃圾、可回收物和其他垃圾一共占生活垃圾的几分之几?
13.客车和货车同时从两地相对而行,已知客车行完全程要15分钟,货车每分钟行300米,当客车行了全程的时,与货车相遇,货车行了多少米?
14.一个圆柱形油桶,底面直径是6分米,高是8分米,装满了油,把桶里的油倒出后,还剩多少升油?
15.一个圆柱形水桶高60厘米,里面水深达,浸入一块12立方分米的石块后,水深变为。该水桶的容积是多少?
16.解放路小学六年级有学生306人,选出男生的和12名女生参加区上组织的“六一”儿童节文艺汇演,选好后剩下的男、女生人数恰巧一样多。解放路小学六年级男、女生各多少人?
17.有一个圆锥形容器,它的底面直径是2分米,高是15厘米,把它装满水后,全部倒入从里面量长是12厘米、宽是10厘米的长方体水槽中,水面的高度正好是水槽高的,这个水槽的高是多少厘米?(得数精确到十分位)
18.东风机械厂有两个车间,甲车间人数是乙车间人数的,如果从乙车间调18人到甲车间,则两个车间人数相等,甲、乙两个车间原来各有多少人?
19.为响应“绿水青山就是金山银山”号召,学校组织五、六年级积极开展植树活动。两个年级共植树96棵,其中五年级植树棵数是六年级的。五、六年级各植树多少棵?
20.甲、乙两个工程队合修一条水渠,甲工程队先修了4500米后,乙工程队修了剩下的,还剩2000米。这条水渠长多少米?
21.每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。笑笑家为了节约用水,做了一个无盖圆柱形铁皮水桶蓄水,高10分米,底面直径是高的,做这个水桶至少要用多少平方分米的铁皮?
22.为保障疫情期间的医疗物资供应,全国各地医疗物资生产企业加班加点生产,某企业接到生产一批防护服的任务,第一天生产的套数与总套数的比是1∶5,第二天生产了660套防护服,两天完成的套数比未完成的套数少。这批防护服的生产任务共是多少套?
23.一批水果,卖出这批水果的,这时剩下的比卖出的多150千克。这批水果原来一共多少千克?
24.习爷爷提出“绿水青山就是金山银山”。科研人员在西北某沙漠的一个区域种植胡杨800棵,种植沙柳的是胡杨棵数的,又是沙枣棵数的,这个区域种植沙枣树多少棵?
1.70人
【分析】把男生人数看作单位“1”,女生人数是男生人数的,用乘法计算。得出女生人数,再减男生人数即可。
【详解】
(人)
答:男生比女生少70人。
2.5天
【分析】将这项工程的工作量当作单位“1”,则甲、乙的工作效率分别、,则乙单独做3天能完成总工作量×3=,其余的1-由他们合做完成,则根据工作量÷工作效率=工作时间可知,甲、乙合做的天数为(1-)÷()。
【详解】(1-×3)÷()
=(1-×3)÷()
=(1-×3)÷
=(1-)÷
=÷
=×
=
=5(天)
答:甲、乙合做了5天。
3.66个
【分析】用我们城市总个数乘30%,得出供水不足的城市个数,再乘,即为严重缺水的城市有多少个,据此解答。
【详解】
(个)
答:这些城市中,严重缺水的城市有66个。
【点睛】解答本题的关键是要掌握已知一个数,求它的几分之几是多少,用乘法计算;求一个数的百分之几是多少,用乘法计算。
4.4次
【分析】把这批蔬菜看作单位“1”,根据工作总量÷工作时间=工作效率,据此分别求出小汽车的工作效率为,大卡车的工作效率为,再根据工作总量÷工作效率之和=工作时间,据此进行计算即可。
【详解】1÷(+)
=1÷
=4(次)
答:如果两辆车一起运,4次才能运完。
【点睛】本题考查工程问题,明确工作总量、工作时间和工作效率之间的关系是解题的关键。
5.原来第一车间有170人,第二车间有250人
【分析】根据“第一车间的人数比第二车间人数的少30人”,可知第二车间人数第一车间人数;又“从第二车间调10人到第一车间,这时第一车间的人数是第二车间人数的”,可知第一车间人数(第二车间人数;据此可设原来第二车间有人,那么第一车间就有人;进而列方程得解。
【详解】解:设原来第二车间有人,那么第一车间就有人。
第一车间有:(人)。
答:原来第一车间有170人,第二车间有250人。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为,另一个未知数用含的式子来表示,进而列并解方程即可。
6.4天
【分析】将工作总量看作单位“1”,时间分之一可以看作效率,这项工程的÷两队效率和=合作天数,据此列式解答。
【详解】÷(+)
=÷
=×6
=4(天)
答:两人合作需要4天完成这项工程的。
【点睛】关键是理解工作效率、工作时间、工作总量之间的关系。
7.20人
【分析】由题意可知,将不变量看作单位“1”,男生人数不变,所以将男生人数看作单位“1”,则原来的女生人数占男生人数的,现在的女生人数占男生人数的,根据部分的量÷所对应的分率=单位“1”的量,求出男生人数,再进一步求出女生人数即可。
【详解】4÷(-)
=4÷(-)
=4÷
=30(人)
30×=30×=20(人)
答:六(1)班现在有女生20人。
【点睛】本题考查分数除法,明确将不变的量看作单位“1”是解题的关键。
8.1000元
【分析】先把用完总钱数的后剩下的钱数看作单位“1”,饮水机的钱数加上多出的20元刚好占单位“1”的(1-),根据“量÷对应的分率”求出用完总钱数的后剩下的钱数,再把妈妈一共带的钱数看作单位“1”,从剩下的钱数里面拿出100元给洗漱用品花的钱数,则(900-100)元占全部钱数的(1-),根据“量÷对应的分率”求出妈妈带的总钱数,据此解答。
【详解】
(580+20)÷(1-)
=600÷
=900(元)
(900-100)÷(1-)
=800÷
=1000(元)
答:果果妈妈一共带了1000元钱。
【点睛】本题属于比较复杂的分数除法应用题,两个分数的单位“1”不相同,找出量和对应的分率是解答题目的关键。
9.鸡:2800只;鸭:3500只
【分析】将鸭子的数量看成单位“1”,鸡的只数是鸭的,则6300只对应鸭子的数量的(1+)=,根据分数除法的意义,用6300÷即可求出鸭子的数量;再用总数量减去鸭子的数量,即可求出鸡的数量,据此解答。
【详解】6300÷(1+)
=6300÷
=3500(只)
6300-3500=2800(只)
答:青山饲养场今年养鸡2800只,养鸭3500只。
【点睛】此题考查了分数除法的应用,找出与已知量对应的分率是解答此类问题的关键。
10.超重;不超重的书包质量为4.5千克,王明的书包质量超过了4.5千克,所以书包超重。
【分析】先用分数乘法求出王明体重的,再和书包的质量比较大小,如果结果大于5千克,书包不超重,如果结果小于5千克,书包超重,据此解答。
【详解】30×=4.5(千克)
因为5千克>4.5千克,所以书包超重。
答:书包超重,因为不超重的书包质量为4.5千克,王明的书包质量超过了4.5千克,所以书包超重。
【点睛】已知一个数,求这个数的几分之几是多少用分数乘法计算。
11.500米
【分析】根据题意,阿雷西博天文望远镜的直径比“中国天眼”的直径短,把“中国天眼”的直径看作单位“1”,阿雷西博天文望远镜的直径是“中国天眼”的直径的(1-),单位“1”未知,用阿雷西博天文望远镜的直径除以(1-),即可求出“中国天眼”的直径。
【详解】350÷(1-)
=350÷
=350×
=500(米)
答:“中国天眼”的直径是500米。
【点睛】本题考查分数除法的意义及应用,明确已知比一个数多或少几分之几是多少,求这个数,用除法计算。
12.
【分析】把生活垃圾看作单位“1”,根据加法的意义,用加法求出厨余垃圾、可回收物、其他垃圾占生活垃圾的分率之和即可。
【详解】
答:这个小区产生的厨余垃圾、可回收物和其他垃圾一共占生活垃圾的。
【点睛】本题考查分数加法的应用,掌握异分母分数加法的计算法则是解题的关键。
13.2700米
【分析】由题意可知,两车相遇时,客车和货车行驶的时间是一样的,然后把两地的距离看作单位“1”,根据路程÷时间=速度,据此可求出客车的速度是,然后再根据路程÷速度=时间,据此求出客车行驶的时间,最后根据速度×时间=路程,据此出货车行驶的距离。
【详解】÷=9(分钟)
300×9=2700(米)
答:与货车相遇,货车行了2700米。
【点睛】本题考查路程、时间和速度之间的关系,明确两车相遇时,客车和货车行驶的时间是一样的是解题的关键。
14.56.52升
【分析】根据圆柱的体积公式:底面积×高,把数代入即可求出圆柱形油桶的体积,再根据1立方分米=1升,转换单位,由于倒出桶里的后,单位“1”是桶里的量,单位“1”已知,用乘法,用桶里的量×,之后再用桶里的量减去用掉的即可求出剩下的。
【详解】3.14×(6÷2)2×8
=3.14×9×8
=226.08(立方分米)
226.08立方分米=226.08升
226.08×=169.56(升)
226.08-169.56=56.52(升)
答:还剩56.52升。
【点睛】本题主要考查圆柱的体积公式,熟练掌握它的体积公式并灵活运用,同时要注意体积和容积的换算。
15.80立方分米
【分析】根据圆柱的体积(容积)公式V=Sh,水桶的底面积不变,所以高的比等于体积的比,把水桶的高看作单位“1”,原来的水深占水桶高的,浸入一块12立方分米的石块后,水深变为。据此可以求出水面上升的高占水桶高的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】12÷(-)
=12÷
=80(立方分米)
答:该水桶的容积是80立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式。
16.男生:154人;女生:152人
【分析】设男生有x人,则女生有(306-x)人,选出男生的是x人,剩下的男生有(x-x)人,选出12名女生,女生还剩(306-x-12)人,剩下的男生和女生人数一样,列方程:x-x=306-x-12,解方程,即可解答。
【详解】解:设男生有x人,女生有(306-x)人。
x-x=306-x-12
x+x=294
x=294
x=294÷
x=294×
x=154
女生有:306-154=152(人)
答:解放路小学六年级男生有154人,女生有152人。
【点睛】根据方程的实际应用,利用男生人数、女生人数和总人数之间的关系,设出未知数,找出相关的量,列方程,解方程。
17.26.2厘米
【分析】根据圆锥的体积公式:V=Sh,据此求出水的体积,然后根据长方体的体积公式:V=abh,据此求出水面的高度,水面的高度正好是水槽高的,根据除法的意义,用除法解答即可。
【详解】2分米=20厘米
×3.14×(20÷2)2×15÷(12×10)÷
=×3.14×100×15÷120÷
=1570÷120÷
=1570÷(120×)
=1570÷60
≈26.2(厘米)
答:这个水槽的高是26.2厘米。
【点睛】本题考查圆锥和长方体的体积,熟记公式是解题的关键。
18.甲车间原来有60人,乙车间原来有96人
【分析】把乙车间原来的人数看作单位“1”,由题意可知,乙车间比甲车间多2个18人,即(18×2)人,这(18×2)人正好是乙车间人数的(1-),根据分数除法的意义,用(18×2)人除以(1-),就是乙车间原来的人数。再根据分数乘法的意义,用乙车间原来的人数乘,就是甲车间原来的人数。
【详解】18×2÷(1-)
=36÷
=96(人)
96×=60(人)
答:甲车间原来有60人,乙车间原来有96人。
【点睛】此题是考查分数乘、除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
19.40棵;56棵
【分析】把六年级植树棵数看作单位“1”,则五年级植树棵数是,两个年级植树棵数是(1+),根据分数除法的意义,用两个年级共植树棵数除以(1+),就是六年级植树棵数;再根据分数乘法的意义,用六年级植树棵数乘,就是五年级植树棵数。
【详解】96÷(1+)
=96÷
=56(棵)
56×=40(棵)
答:五年级植树40棵,六年级植树56棵。
【点睛】此题是考查分数乘、除法的意义及应用。求一个数的几分之几是多少,用这个数乘分率;已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率。
20.11500米
【分析】把甲工程队先修后剩下的长度看作单位“1”,甲工程队先修了4500米后,乙工程队修了剩下的,还剩2000米,那么可知2000米占甲工程队先修后剩下的长度的(1-),用除法计算即可求出甲工程队先修后剩下的长度,然后再加上甲工程队先修的4500米,即可求出这条水渠长多少米。
【详解】2000÷(1-)+4500
=2000÷+4500
=7000+4500
=11500(米)
答:这条水渠长11500米。
【点睛】本题关键是把甲工程队先修后剩下的长度看作单位“1”,求出甲工程队先修后剩下的长度是解题的关键。
21.138.16平方分米
【分析】因为底面直径是高的,高是8分米,所以底面直径为:10×=4(分米)。因为是无盖水桶,所以它的表面积等于圆柱的侧面积加上底面积即可。
【详解】10×=4(分米)
3.14×4×10+3.14×(4÷2)2
=125.6+12.56
=138.16(平方分米)
答:这个水桶至少要用铁皮138.16平方分米。
【点睛】本题的解答关键在于先求出底面直径,再根据圆柱的表面积公式即可解答。
22.2700套
【分析】设这批防护服的生产任务一共是x套,第一天生产的套数与总套数的比是1∶5,第一天生产x(套),根据等量关系:两天完成的套数=未完成的套数×(1-),列方程解答即可。
【详解】解:设这批防护服的生产任务一共是x套。
x+660=(x-x-660)×(1-)
x+660=(x-660)×
x+660=x-528
x=1188
x=2700
答:这批防护服的生产任务一共是2700套。
【点睛】本题主要考查了比及分数的应用,关键是根据等量关系:两天完成的套数=未完成的套数×(1-),列方程。
23.750千克
【分析】把这批水果的千克数看作单位“1”,卖出这批水果的,剩下这批水果的(1-),由此可知150千克相当于这批水果的(1--),根据已知一个数的几分之几是多少,求这个数,用除法求出这批水果的千克数即可。
【详解】150÷(1--)
=150÷
=750(千克)
答:这批水果原来一共750千克。
【点睛】此题属于基本的分数四则复合应用题,解题的关键是正确找出单位“1”和150千克对应的分率。
24.600棵
【分析】把胡杨的棵数看作单位“1”,单位“1”已知,根据分数乘法的意义,用800乘求出沙柳的棵数,接着把沙枣的棵数看作单位“1”,单位“1”未知,根据分数除法的意义,用沙柳的棵数除以,即可求出沙枣树的棵数。
【详解】800×÷
=500÷
=600(棵)
答:这个区域种植沙枣树600棵。
【点睛】此题主要考查分数乘除法的意义,注意前后两个单位“1”的不同。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
