小升初解决问题专题07:平面图形应用题-2024-2025学年数学六年级下册苏教版(含解析)
文档属性
| 名称 | 小升初解决问题专题07:平面图形应用题-2024-2025学年数学六年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 17:10:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初解决问题专题07:平面图形应用题
1.(1)学校要给会议桌桌面贴上保护膜,至少需要保护膜多少平方米?
(2)开会时每个人需要0.5米宽的位置就坐,这张会议桌大约能坐多少人?
2.王叔叔承包了一块长150米,宽80米的果园种苹果树,株距4米,行距5米。
(1)这个果园能种多少棵苹果树?
(2)平均每棵苹果树能产苹果25千克,每千克苹果批发价为4.6元,果园产的苹果全部按上面的价格售出,王叔叔能收入多少元?
3.新建成的净瓶山新桥桥梁及引道全长约1016米,一辆汽车的轮子半径为40厘米,若每秒钟转6圈,1分钟能完全通过这座桥吗?
4.如图,每个小正方形都相同,涂色部分是一个直角三角形,它的周长是60厘米,这个三角形的面积是多少平方厘米?
5.中心广场摆了一个直径10米的圆形花坛,为了美观,园艺师给花坛围了一圈栅栏,这圈栅栏的长度是多少米?(取3.14)
6.春节要到了,妈妈想给家里的圆桌配上一张大小完全相同的垫子。在实际购买时,她该如何告诉销售人员她家圆桌面的大小呢?怎么能得到想要的数据呢?请帮妈妈想想办法,写出你的思考过程。
(1)用什么数据描述桌面的大小呢?
(2)如何得到想要的数据?
7.淘淘有一个半径为10厘米的鲜花饼,他把鲜花饼切成若干个大小相同的小扇形,分给其他小朋友吃。奇奇取走3块以后(如下图所示),剩下的这块鲜花饼一个面的周长有多少厘米?
8.如下图,已知厘米,厘米,三角形和三角形的面积各占长方形面积的,求三角形的面积。
9.淘气家有一张可折叠的餐桌,把四周折叠的部分收起来,是一张正方形餐桌;把四周折叠的部分撑开,是一张圆形餐桌,这时圆形餐桌的直径是2米。
(1)这张圆形餐桌的面积是多少?
(2)如果一个人需要0.5米的位置就餐,这张圆形餐桌大约坐多少人?
(3)如果在正方形餐桌内放一个最大的转盘(如图),这个转盘有多大?
10.如图,平行四边形的周长是51厘米,以为底边时,高为7厘米;以为底时,高为10厘米,求平行四边形的面积。
11.一只羊被30米长的绳子拴在了正方形建筑物的一个顶点上,建筑物的边长是20米,周围全是草地。这只羊能吃到草的草地面积是多少平方米?(π≈3)
12.在学校的科技小制作活动中,有两个机器人在进行移动操作。一个机器人的形状是直径为10厘米的圆形,另一个是边长为10厘米的正方形。它们在一条长轨道上,初始时两者相距28厘米。正方形机器人每秒移动4厘米,圆形机器人比正方形机器人快40%。
(1)当圆形机器人和正方形机器人刚好完全接触(重叠面积最大时),没有重合部分的面积是多少?
(2)正方形和圆形同时开始运动,经过多少秒后恰好完全分开?
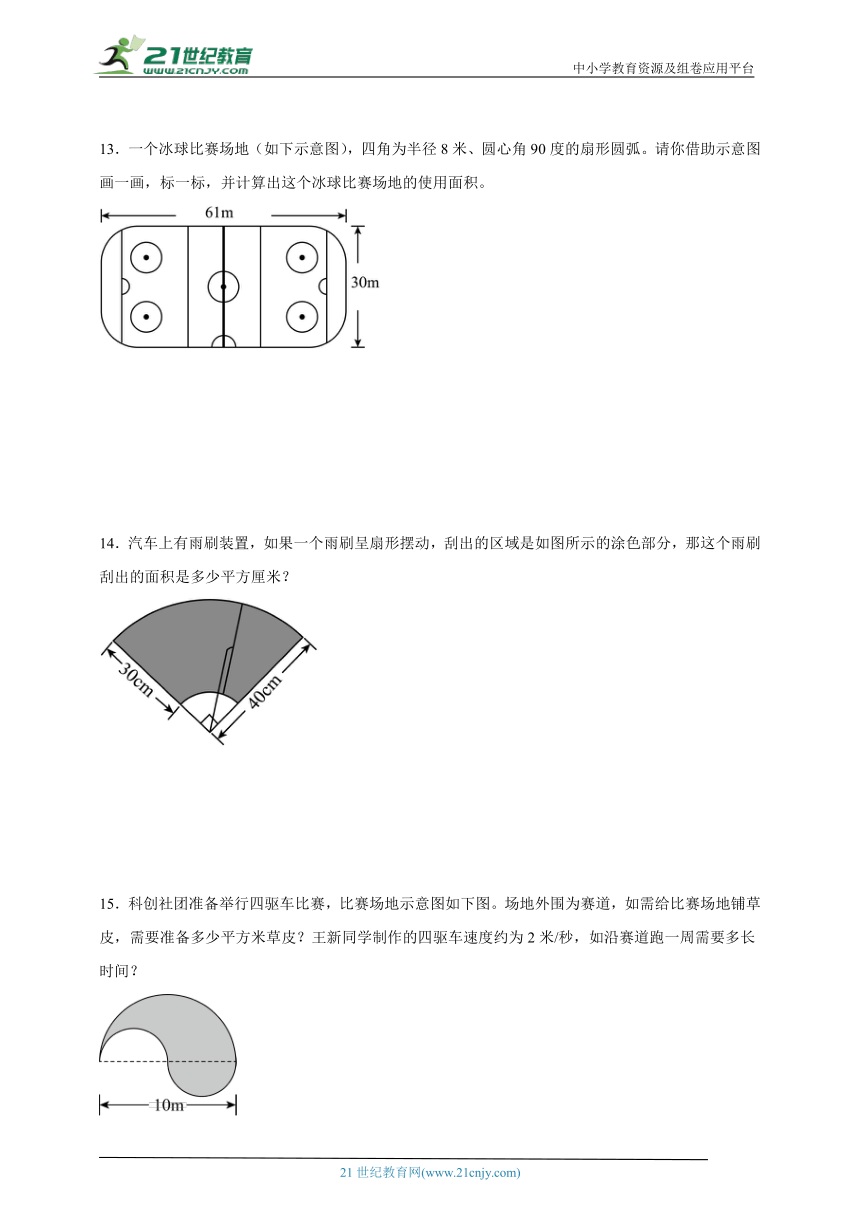
13.一个冰球比赛场地(如下示意图),四角为半径8米、圆心角90度的扇形圆弧。请你借助示意图画一画,标一标,并计算出这个冰球比赛场地的使用面积。
14.汽车上有雨刷装置,如果一个雨刷呈扇形摆动,刮出的区域是如图所示的涂色部分,那这个雨刷刮出的面积是多少平方厘米?
15.科创社团准备举行四驱车比赛,比赛场地示意图如下图。场地外围为赛道,如需给比赛场地铺草皮,需要准备多少平方米草皮?王新同学制作的四驱车速度约为2米/秒,如沿赛道跑一周需要多长时间?
16.如下图,在半圆形空地上有一个三角形区域种植郁金香。郁金香的种植面积为12平方米,其余部分铺草坪。草坪的面积是多少平方米?
17.某款车上安装的雨刷是在一个摆臂上安装胶条,只有胶条才能把挡风玻璃上的灰尘刷干净,如图所示。这款车上雨刷摆臂长度60厘米,胶条长度是40厘米,摇摆角度是180°,那么这种雨刷能刷到的面积是多少平方厘米?
18.乐乐很喜欢用圆规来绘制一些图案,这天她用圆规在方格纸上画了一片“花瓣儿”。已知小方格纸的边长是10厘米,请你算算看:
(1)这片“花瓣儿”的周长是多少厘米?
(2)求这片“花瓣儿”的面积。
19.在乐客商场停车场的出入口有车辆出入的起落杆(如图),当车进出时或出时这根起落杆就要完成一次升降运动。欢欢的爸爸在商场购完物开车出停车场后,这时起落杆A点总共移动了多少米?
20.学校运动会举行200米赛跑,相邻两跑道如图所示,弯道为半圆形,每根跑道宽为1.2米。体育老师在画场地时,要保证两人跑的距离相等,应让外跑道的运动员前移多少米?
21.下图中正方形的边长是6厘米,分别以正方形的边长为半径和直径,作扇形、圆,求阴影部分的面积。(π取3.14)
22.一个长方形的周长是56厘米,长和宽的比是5∶2。这个长方形的长和宽分别是多少厘米?面积是多少平方厘米?
23.在下图中,长方形的面积和圆的面积相等,已知阴影部分的面积是9.42平方厘米,求长方形的长是多少?阴影部分的周长是多少?
24.下图阴影部分的面积是30平方厘米,求环形的面积(大圆与小圆面积差)。
1.(1)11.14平方米
(2)28人
【分析】(1)通过平移,两边可以拼成一个圆,保护膜的面积=圆的面积+长方形面积,圆的面积=圆周率×半径的平方,长方形面积=长×宽,据此列式解答;
(2)会议桌的周长=圆的周长+长方形的长×2,圆的周长=圆周率×直径,据此求出会议桌的周长,会议桌的周长÷每个人需要的宽度=坐的人数,结果用去尾法保留整数。
【详解】(1)3.14×(2÷2)2+4×2
=3.14×12+8
=3.14×1+8
=3.14+8
=11.14(平方米)
答:至少需要保护膜11.14平方米。
(2)3.14×2+4×2
=6.28+8
=14.28(米)
14.28÷0.5≈28(人)
答:这张会议桌大约能坐28人。
2.(1)600棵
(2)69000元
【分析】(1)根据长方形面积公式:面积=长×宽,代入数据,求出果园的占地面积;用株距×行距,求出每棵苹果树占地面积,再用果园占地面积÷每棵苹果树占地面积,求出这个果园能种苹果树的棵数。
(2)用每棵苹果树能产苹果的重量×苹果树的棵数,求出一共能产苹果的重量,再根据总价=单价×数量,用每千克苹果批发价×一共能产苹果的重量,即可解答。
【详解】(1)(150×80)÷(4×5)
=12000÷20
=600(棵)
答:这个果园能种600棵苹果树。
(2)4.6×(25×600)
=4.6×15000
=69000(元)
答:王叔叔能收入69000元。
3.不能
【分析】根据圆周长公式:C=2πr,代入数据即可求出轮子1圈的周长,再乘6即可求出1秒钟轮子走过的周长,已知1分钟有60秒,则用1秒钟轮子走过的周长×60即可求出1分钟轮子走过的总长度,再把单位换算成米,然后和1016比较即可。
【详解】1分钟=60秒
2×3.14×40×6×60
=251.2×6×60
=90432(厘米)
90432厘米=904.32米
904.32米<1016米
答:1分钟不能完全通过这座桥。
4.150平方厘米
【分析】根据题意可知,每个小正方形都相同,所以三条边的比是3∶4∶5,再根据按比分配的方法,求出这个直角三角形的两条直角边的长度,再根据“三角形的面积=底×高÷2”,把数据代入公式解答。
【详解】三角形三条边的比为:3∶4∶5。
60×
=60×
=15(厘米)
60×
=60×
=20(厘米)
15×20÷2
=300÷2
=150(平方厘米)
答:这个三角形的面积是150平方厘米。
5.31.4米
【分析】求这圈栅栏的长度就是求圆形花坛的周长,已知圆形花坛的直径利用“”求出圆形花坛的周长,据此解答。
【详解】3.14×10=31.4(米)
答:这圈栅栏的长度是31.4米。
6.(1)直径
(2)见详解
【分析】(1)根据题意,要给圆桌配上一张大小完全相同的垫子,根据圆的特性“在同一个圆内,所有的直径相等;圆内的所有线段中,直径最长”,购买垫子时,告诉销售人员圆桌的直径即可买到合适的垫子。
(2)想得到圆桌的直径,可以根据“直径是圆内最长的线段”,用米尺测量出圆桌的直径;也可以测量出圆桌的周长,再利用圆的周长公式C=πd,得到圆桌的直径。
【详解】(1)用圆桌的直径来描述桌布的大小。
(2)先用绳子绕圆桌边缘一周,再用卷尺测量绳子的长度,也就是桌子的周长;然后根据圆的直径=周长÷π,得到圆桌的直径。(答案不唯一)
7.67.1厘米
【分析】由图可知,整个圆被平均分成了12份,奇奇取走之后还剩下(12-3)份,图中曲线部分长度占整个圆周长的,利用“”求出曲线部分的长度,最后加上2条半径的长度,据此解答。
【详解】(12-3)÷12
=9÷12
=
=
=
=
=
=67.1(厘米)
答:剩下的这块鲜花饼一个面的周长有67.1厘米。
8.平方厘米
【分析】利用“长方形面积=长×宽”求出长方形的面积,再将长方形看作单位“1”,将长方形面积乘,求出三角形ABE、三角形ADF的面积。三角形面积=底×高÷2,那么将三角形ABE面积乘2除以底AB,即可求出高BE。同理,用三角形ADF面积乘2除以底AD,即可求出高DF。用BC减去BE,求出CE。用CD减去DF,求出CF。再根据三角形面积公式求出三角形CEF的面积。将长方形面积减去三角形ABE、三角形ADF和三角形CEF的面积,即可求出三角形AEF的面积。
【详解】长方形面积:10×6=60(平方厘米)
三角形ABE或三角形ADF的面积:60×=20(平方厘米)
BE:20×2÷6=(厘米)
DF:20×2÷10=4(厘米)
CE:10-=(厘米)
CF:6-4=2(厘米)
三角形CEF面积:×2÷2=(平方厘米)
三角形AEF面积:60-20-20-=(平方厘米)
答:三角形的面积是平方厘米。
【点睛】掌握三角形的面积公式,以及长方形的面积公式,是解答本题的关键。
9.(1)3.14平方米
(2)12人
(3)1.57平方米
【分析】(1)半径=直径÷2,据此求出半径长度;圆的面积=π×半径×半径,代入数值求出圆形餐桌的面积即可;
(2)圆的周长=直径×π,据此求出圆形桌的周长,再用周长除以一个人占的数量,除不尽时用去尾法保留整数,即可求出这张圆形餐桌大约能坐多少人;
(3)如图所示,圆形转盘的直径就是正方形的边长,半径就是边长,圆的面积=π×半径×半径,所以圆盘面积=π×边长×边长=×边长×边长,而边长×边长=正方形面积,所以圆盘面积=×正方形面积;连接正方形的对角线,分成4个相同的小三角形,对角线就是圆的直径,也就是2米,小三角的底是对角线的一半,也就是1米,高也是对角线的一半,也是1米,根据三角形的面积=底×高÷2求出一个小三角形的面积,再乘4就是正方形的面积。最后把正方形面积乘即可求出圆盘面积。
【详解】(1)2÷2=1(米)
3.14×1×1=3.14(平方米)
答:这张圆形餐桌的面积是3.14平方米。
(2)3.14×2=6.28(米)
6.28÷0.5=12.56≈12(人)
答:这张圆形餐桌大约坐12人。
(3)2÷2=1(米)
1×1÷2×4=2(平方米)
×2=1.57(平方米)
答:这个转盘有1.57平方米。
10.105平方厘米
【分析】根据平行四边形的面积=底×高,由题意可知,CD×7=BC×10,假设它们的积为1,用1分别除以7和10,再用商列比并化简,可分别得CD和BC的比,根据比的应用,用51除以2再除以CD和BC对应的份数和,得到每份的长度,再用每份长度乘BC对应的份数,得BC的长,再代入面积公式计算即可。
【详解】假设CD×7=BC×10=1
CD∶BC=
(厘米)
(平方厘米)
则平行四边形的面积是105平方厘米。
【点睛】根据等量关系CD×7=BC×10,确定CD和BC的比,转化为比的应用题。
11.2175平方米
【分析】如下图,正方形建筑物的边长是20米,羊被30米长的绳子拴在了正方形建筑物的一个顶点上,那么羊吃草的面积=半径为30米的圆的面积+2个半径为(30-20)米的圆的面积;根据圆的面积公式S=πr2,代入数据计算即可求解。
【详解】3×302×+3×(30-20)2××2
=3×900×+3×102××2
=2025+3×100××2
=2025+150
=2175(平方米)
答:这只羊能吃到草的草地面积是2175平方米。
12.(1)21.5平方厘米
(2)5秒
【分析】(1)重叠时,圆在正方形内,相当于正方形内画一个最大的圆,求没有重合部分的面积,就是用正方形面积-圆的面积;根据正方形面积公式:面积=边长×边长,圆的面积公式:面积=π×半径2,代入数据,即可解答。
(2)把正方形机器人的速度看作单位“1”,圆形机器人的速度是正方形机器人速度的(1+40%),用正方形机器人的速度×(1+40%),求出圆形机器人的速度。求经过多少秒后恰好完全分开,先求出正方形机器人走过的路程与圆形机器人走过的路程和,正方形机器人与圆形机器人相距的距离+正方形机器人的边长的长度+圆形机器人的直径的长度,就是两个机器人完全分开后的路程,再根据时间=路程÷速度,用正方形机器人走过的路程与圆形机器人走过的路程和÷正方形机器人的速度与圆形机器人的速度和,即可解答。
【详解】(1)10×10-3.14×(10÷2)2
=10×10-3.14×52
=100-3.14×25
=100-78.5
=21.5(平方厘米)
答:没有重合部分的面积是21.5平方厘米。
(2)4×(1+40%)
=4×140%
=5.6(厘米)
(28+10+10)÷(4+5.6)
=(38+10)÷9.6
=48÷9.6
=5(秒)
答:经过5秒后恰好完全分开。
【点睛】解答本题的关键是求出正方形机器人与圆形机器人走过的路程。
13.图见详解;1774.96平方米
【分析】如下图,把这个冰球场地分成4个半径为8米的圆、中间是一个长61米、宽(30-8-8)米的长方形、上下是两个完全一样的长为(61-8-8)米、宽为8米的长方形;根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】如图:
3.14×82××4
=3.14×64××4
=200.96(平方米)
61×(30-8-8)
=61×14
=854(平方米)
(61-8-8)×8×2
=45×8×2
=720(平方米)
200.96+854+720
=1054.96+720
=1774.96(平方米)
答:这个冰球比赛场地的使用面积是1774.96平方米。
14.1177.5平方厘米
【分析】这个雨刷刮出的面积等于以40厘米为半径的圆面积的减去以(40-30)厘米为半径的圆面积的,根据圆的面积=×半径的平方,代入数据解答即可。
【详解】40-30=10(厘米)
3.14××-3.14××
=3.14×1600×-3.14×100×
=3.14×400-3.14×25
=1256-78.5
=1177.5(平方厘米)
答:这个雨刷刮出的面积是1177.5平方厘米。
15.39.25平方米;15.7秒
【分析】观察图形可知:比赛场地是一个不规则图形,右下角的小半圆可以填补到左边的空白半圆处,这样比赛场地就变为一个以10米为直径的半圆,根据圆的面积=πr2,求出圆的面积,再除以2即可求出需要草皮的面积。
观察图形可知:比赛场地周长的上半部分是以10米为直径的圆的周长的一半,下半部分的两条半圆弧可以组成以(10÷2)米为直径的圆。根据圆的周长=πd,分别求出两部分的长度,再把它们相加可以求出比赛场地的周长。最后根据路程÷速度=时间,用场地的周长除以2,即可求出沿赛道跑一周需要多长时间。
【详解】(10÷2)2×3.14÷2
=52×3.14÷2
=25×3.14÷2
=39.25(平方米)
10×3.14÷2+10÷2×3.14
=15.7+15.7
=31.4(米)
31.4÷2=15.7(秒)
答:需要准备39.25平方米草皮;沿赛道跑一周需要15.7秒。
16.
25.68平方米
【分析】观察可知,草坪的面积等于半圆面积减三角形面积,已知三角形是直角等腰三角形,两条直角边都等于半圆的半径,根据的逆运算,用三角形面积乘2得到r2,再根据圆的面积公式,圆的面积除以2可得到半圆的面积,代入数据计算即可得解。
【详解】r2=(平方米)
(平方米)
答:草坪的面积是25.68平方米。
17.
5024平方厘米
【分析】雨刷摇摆角度是180°,求雨刷能刷到的面积,就是一个环形面积的一半,环形的,,根据环形的面积公式,用环形的面积再除以2即可得解。
【详解】60-40=20(厘米)
(平方厘米)
答:这种雨刷能刷到的面积是5024平方厘米。
18.(1)62.8厘米;(2)114平方厘米
【分析】(1)看图可知,花瓣的周长是由两个半径是10厘米的四分之一圆的弧长,以及一个半径是(10×2)厘米的四分之一圆的弧长。圆周长=2πr,据此先求出半径是10厘米圆的周长,再除以4乘2,求出两个半径是10厘米的四分之一圆的弧长。再根据圆周长公式求出半径是(10×2)厘米圆的周长,再除以4,求出半径是(10×2)厘米的四分之一圆的弧长。将这两部分相加,即可求出这片“花瓣儿”的周长。
(2)如图:连接大正方形左下角和右上角的顶点,画出一条对角线。根据画好的图可知,这片花瓣在对角线上方的部分是可以剪拼到左下方的。圆面积=πr2,据此求出半径是(10×2)厘米圆的面积。将圆面积除以4,求出四分之一圆的面积。三角形面积=底×高÷2,据此求出三角形的面积。将四分之一圆的面积减去三角形的面积,即可求出花瓣的面积。
【详解】(1)2×3.14×10÷4×2+2×3.14×(10×2)÷4
=2×3.14×10÷4×2+2×3.14×20÷4
=62.8÷4×2+125.6÷4
=31.4+31.4
=62.8(厘米)
答:这片“花瓣儿”的周长是62.8厘米。
(2)如图:
10×2=20(厘米)
3.14×202÷4-20×20÷2
=3.14×400÷4-20×20÷2
=314-200
=114(平方厘米)
答:这片“花瓣儿”的面积是114平方厘米。
19.10.99米
【分析】根据题意,起落杆完成一次升降运动,起落杆A点移动了2个半径为3.5米的圆周长的;根据圆的周长公式C=2πr,代入数据计算求出起落杆A点总共移动的长度。
【详解】2×3.14×3.5××2=10.99(米)
答:这时起落杆A点总共移动了10.99米。
20.3.768米
【分析】观察图形可知,200米赛跑的直道长度一定,但相邻内、外半圆的圆弧长度有差距,所以相邻跑道的起跑线的差距等于相邻内、外半圆的圆弧长度差。
根据圆的周长公式C=2πr可知,半圆弧长=2πr÷2=πr,相邻外半圆与内半圆的圆弧长之差为πR-πr=π(R-r),已知跑道宽为1.2米,即R-r=1.2米,由此得出,200米赛跑相邻跑道的起跑线的差距=π×跑道宽,代入数据计算即可得解。
【详解】3.14×1.2=3.768(米)
答:应让外跑道的运动员前移3.768米。
21.11.61平方厘米
【分析】
如图所示,在一个正方形里面有一个最大的圆,这个圆的直径是这个正方形的边长。可以观察发现正方形减去圆,剩下正方形四个角上一模一样的图形(S1),每一个S1的面积=(正方形的面积-圆的面积)÷4,根据正方形的面积=边长×边长、圆的面积=计算出一个S1的面积;根据各部分之间的关系,可知阴影部分的面积=(正方形的面积-半径是6厘米圆的面积-S1)×2,据此代入数值计算即可。
【详解】6×6=36(平方厘米)
(平方厘米)
S1面积:(36-28.26)÷4
=7.74÷4
=1.935 (平方厘米)
阴影部分面积:(36--1.935)×2
=(36- 28.26-1.935)×2
=5.805×2
=11.61(平方厘米)
答:阴影部分的面积为11.61平方厘米。
【点睛】找出如何得出阴影部分面积的方法,再利用基础图形的公式计算。
22.20厘米;8厘米;160平方厘米
【分析】长方形的周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数=一份数,一份数分别乘长和宽的对应份数,即可求出长和宽,再根据长方形面积=长×宽,即可求出面积。
【详解】56÷2÷(5+2)
=28÷7
=4(厘米)
4×5=20(厘米)
4×2=8(厘米)
20×8=160(平方厘米)
答:这个长方形的长和宽分别是20厘米、8厘米,面积是160平方厘米。
23.6.28厘米;15.74厘米
【分析】由题可知,长方形的面积和圆的面积相等,阴影部分的面积是9.42平方厘米,则阴影部分占整个圆的,用阴影部分的面积除以,求出圆和长方形的面积,又知长方形的宽等于圆的半径,根据圆的面积=πr2,求出圆的半径,再用长方形的面积除以宽,求出长方形的长;阴影部分的周长由四部分组成:圆周长的,长方形的长,长方形的宽以及长方形长与宽之间的差;根据圆的周长=2πr,分别计算出圆周长的、长方形长与宽之间的差,最后将四部分相加,得到阴影部分的周长。
【详解】9.42÷
=9.42×
=12.56(平方厘米)
12.56÷3.14=4
4=2×2
所以圆的半径是2厘米。
12.56÷2=6.28(厘米)
3.14×2×2×
=6.28×2×
=12.56×
=3.14(厘米)
6.28-2=4.28(厘米)
3.14+6.28+2+4.28
=9.42+2+4.28
=11.42+4.28
=15.7(厘米)
答:长方形的长是6.28厘米,阴影部分的周长是15.74厘米。
24.94.2平方厘米
【分析】观察可知,阴影部分的面积就是大正方形与小正方形的面积差,即,根据环形的面积=,代入数据计算即可得解。
【详解】(平方厘米)
答:环形的面积是94.2平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初解决问题专题07:平面图形应用题
1.(1)学校要给会议桌桌面贴上保护膜,至少需要保护膜多少平方米?
(2)开会时每个人需要0.5米宽的位置就坐,这张会议桌大约能坐多少人?
2.王叔叔承包了一块长150米,宽80米的果园种苹果树,株距4米,行距5米。
(1)这个果园能种多少棵苹果树?
(2)平均每棵苹果树能产苹果25千克,每千克苹果批发价为4.6元,果园产的苹果全部按上面的价格售出,王叔叔能收入多少元?
3.新建成的净瓶山新桥桥梁及引道全长约1016米,一辆汽车的轮子半径为40厘米,若每秒钟转6圈,1分钟能完全通过这座桥吗?
4.如图,每个小正方形都相同,涂色部分是一个直角三角形,它的周长是60厘米,这个三角形的面积是多少平方厘米?
5.中心广场摆了一个直径10米的圆形花坛,为了美观,园艺师给花坛围了一圈栅栏,这圈栅栏的长度是多少米?(取3.14)
6.春节要到了,妈妈想给家里的圆桌配上一张大小完全相同的垫子。在实际购买时,她该如何告诉销售人员她家圆桌面的大小呢?怎么能得到想要的数据呢?请帮妈妈想想办法,写出你的思考过程。
(1)用什么数据描述桌面的大小呢?
(2)如何得到想要的数据?
7.淘淘有一个半径为10厘米的鲜花饼,他把鲜花饼切成若干个大小相同的小扇形,分给其他小朋友吃。奇奇取走3块以后(如下图所示),剩下的这块鲜花饼一个面的周长有多少厘米?
8.如下图,已知厘米,厘米,三角形和三角形的面积各占长方形面积的,求三角形的面积。
9.淘气家有一张可折叠的餐桌,把四周折叠的部分收起来,是一张正方形餐桌;把四周折叠的部分撑开,是一张圆形餐桌,这时圆形餐桌的直径是2米。
(1)这张圆形餐桌的面积是多少?
(2)如果一个人需要0.5米的位置就餐,这张圆形餐桌大约坐多少人?
(3)如果在正方形餐桌内放一个最大的转盘(如图),这个转盘有多大?
10.如图,平行四边形的周长是51厘米,以为底边时,高为7厘米;以为底时,高为10厘米,求平行四边形的面积。
11.一只羊被30米长的绳子拴在了正方形建筑物的一个顶点上,建筑物的边长是20米,周围全是草地。这只羊能吃到草的草地面积是多少平方米?(π≈3)
12.在学校的科技小制作活动中,有两个机器人在进行移动操作。一个机器人的形状是直径为10厘米的圆形,另一个是边长为10厘米的正方形。它们在一条长轨道上,初始时两者相距28厘米。正方形机器人每秒移动4厘米,圆形机器人比正方形机器人快40%。
(1)当圆形机器人和正方形机器人刚好完全接触(重叠面积最大时),没有重合部分的面积是多少?
(2)正方形和圆形同时开始运动,经过多少秒后恰好完全分开?
13.一个冰球比赛场地(如下示意图),四角为半径8米、圆心角90度的扇形圆弧。请你借助示意图画一画,标一标,并计算出这个冰球比赛场地的使用面积。
14.汽车上有雨刷装置,如果一个雨刷呈扇形摆动,刮出的区域是如图所示的涂色部分,那这个雨刷刮出的面积是多少平方厘米?
15.科创社团准备举行四驱车比赛,比赛场地示意图如下图。场地外围为赛道,如需给比赛场地铺草皮,需要准备多少平方米草皮?王新同学制作的四驱车速度约为2米/秒,如沿赛道跑一周需要多长时间?
16.如下图,在半圆形空地上有一个三角形区域种植郁金香。郁金香的种植面积为12平方米,其余部分铺草坪。草坪的面积是多少平方米?
17.某款车上安装的雨刷是在一个摆臂上安装胶条,只有胶条才能把挡风玻璃上的灰尘刷干净,如图所示。这款车上雨刷摆臂长度60厘米,胶条长度是40厘米,摇摆角度是180°,那么这种雨刷能刷到的面积是多少平方厘米?
18.乐乐很喜欢用圆规来绘制一些图案,这天她用圆规在方格纸上画了一片“花瓣儿”。已知小方格纸的边长是10厘米,请你算算看:
(1)这片“花瓣儿”的周长是多少厘米?
(2)求这片“花瓣儿”的面积。
19.在乐客商场停车场的出入口有车辆出入的起落杆(如图),当车进出时或出时这根起落杆就要完成一次升降运动。欢欢的爸爸在商场购完物开车出停车场后,这时起落杆A点总共移动了多少米?
20.学校运动会举行200米赛跑,相邻两跑道如图所示,弯道为半圆形,每根跑道宽为1.2米。体育老师在画场地时,要保证两人跑的距离相等,应让外跑道的运动员前移多少米?
21.下图中正方形的边长是6厘米,分别以正方形的边长为半径和直径,作扇形、圆,求阴影部分的面积。(π取3.14)
22.一个长方形的周长是56厘米,长和宽的比是5∶2。这个长方形的长和宽分别是多少厘米?面积是多少平方厘米?
23.在下图中,长方形的面积和圆的面积相等,已知阴影部分的面积是9.42平方厘米,求长方形的长是多少?阴影部分的周长是多少?
24.下图阴影部分的面积是30平方厘米,求环形的面积(大圆与小圆面积差)。
1.(1)11.14平方米
(2)28人
【分析】(1)通过平移,两边可以拼成一个圆,保护膜的面积=圆的面积+长方形面积,圆的面积=圆周率×半径的平方,长方形面积=长×宽,据此列式解答;
(2)会议桌的周长=圆的周长+长方形的长×2,圆的周长=圆周率×直径,据此求出会议桌的周长,会议桌的周长÷每个人需要的宽度=坐的人数,结果用去尾法保留整数。
【详解】(1)3.14×(2÷2)2+4×2
=3.14×12+8
=3.14×1+8
=3.14+8
=11.14(平方米)
答:至少需要保护膜11.14平方米。
(2)3.14×2+4×2
=6.28+8
=14.28(米)
14.28÷0.5≈28(人)
答:这张会议桌大约能坐28人。
2.(1)600棵
(2)69000元
【分析】(1)根据长方形面积公式:面积=长×宽,代入数据,求出果园的占地面积;用株距×行距,求出每棵苹果树占地面积,再用果园占地面积÷每棵苹果树占地面积,求出这个果园能种苹果树的棵数。
(2)用每棵苹果树能产苹果的重量×苹果树的棵数,求出一共能产苹果的重量,再根据总价=单价×数量,用每千克苹果批发价×一共能产苹果的重量,即可解答。
【详解】(1)(150×80)÷(4×5)
=12000÷20
=600(棵)
答:这个果园能种600棵苹果树。
(2)4.6×(25×600)
=4.6×15000
=69000(元)
答:王叔叔能收入69000元。
3.不能
【分析】根据圆周长公式:C=2πr,代入数据即可求出轮子1圈的周长,再乘6即可求出1秒钟轮子走过的周长,已知1分钟有60秒,则用1秒钟轮子走过的周长×60即可求出1分钟轮子走过的总长度,再把单位换算成米,然后和1016比较即可。
【详解】1分钟=60秒
2×3.14×40×6×60
=251.2×6×60
=90432(厘米)
90432厘米=904.32米
904.32米<1016米
答:1分钟不能完全通过这座桥。
4.150平方厘米
【分析】根据题意可知,每个小正方形都相同,所以三条边的比是3∶4∶5,再根据按比分配的方法,求出这个直角三角形的两条直角边的长度,再根据“三角形的面积=底×高÷2”,把数据代入公式解答。
【详解】三角形三条边的比为:3∶4∶5。
60×
=60×
=15(厘米)
60×
=60×
=20(厘米)
15×20÷2
=300÷2
=150(平方厘米)
答:这个三角形的面积是150平方厘米。
5.31.4米
【分析】求这圈栅栏的长度就是求圆形花坛的周长,已知圆形花坛的直径利用“”求出圆形花坛的周长,据此解答。
【详解】3.14×10=31.4(米)
答:这圈栅栏的长度是31.4米。
6.(1)直径
(2)见详解
【分析】(1)根据题意,要给圆桌配上一张大小完全相同的垫子,根据圆的特性“在同一个圆内,所有的直径相等;圆内的所有线段中,直径最长”,购买垫子时,告诉销售人员圆桌的直径即可买到合适的垫子。
(2)想得到圆桌的直径,可以根据“直径是圆内最长的线段”,用米尺测量出圆桌的直径;也可以测量出圆桌的周长,再利用圆的周长公式C=πd,得到圆桌的直径。
【详解】(1)用圆桌的直径来描述桌布的大小。
(2)先用绳子绕圆桌边缘一周,再用卷尺测量绳子的长度,也就是桌子的周长;然后根据圆的直径=周长÷π,得到圆桌的直径。(答案不唯一)
7.67.1厘米
【分析】由图可知,整个圆被平均分成了12份,奇奇取走之后还剩下(12-3)份,图中曲线部分长度占整个圆周长的,利用“”求出曲线部分的长度,最后加上2条半径的长度,据此解答。
【详解】(12-3)÷12
=9÷12
=
=
=
=
=
=67.1(厘米)
答:剩下的这块鲜花饼一个面的周长有67.1厘米。
8.平方厘米
【分析】利用“长方形面积=长×宽”求出长方形的面积,再将长方形看作单位“1”,将长方形面积乘,求出三角形ABE、三角形ADF的面积。三角形面积=底×高÷2,那么将三角形ABE面积乘2除以底AB,即可求出高BE。同理,用三角形ADF面积乘2除以底AD,即可求出高DF。用BC减去BE,求出CE。用CD减去DF,求出CF。再根据三角形面积公式求出三角形CEF的面积。将长方形面积减去三角形ABE、三角形ADF和三角形CEF的面积,即可求出三角形AEF的面积。
【详解】长方形面积:10×6=60(平方厘米)
三角形ABE或三角形ADF的面积:60×=20(平方厘米)
BE:20×2÷6=(厘米)
DF:20×2÷10=4(厘米)
CE:10-=(厘米)
CF:6-4=2(厘米)
三角形CEF面积:×2÷2=(平方厘米)
三角形AEF面积:60-20-20-=(平方厘米)
答:三角形的面积是平方厘米。
【点睛】掌握三角形的面积公式,以及长方形的面积公式,是解答本题的关键。
9.(1)3.14平方米
(2)12人
(3)1.57平方米
【分析】(1)半径=直径÷2,据此求出半径长度;圆的面积=π×半径×半径,代入数值求出圆形餐桌的面积即可;
(2)圆的周长=直径×π,据此求出圆形桌的周长,再用周长除以一个人占的数量,除不尽时用去尾法保留整数,即可求出这张圆形餐桌大约能坐多少人;
(3)如图所示,圆形转盘的直径就是正方形的边长,半径就是边长,圆的面积=π×半径×半径,所以圆盘面积=π×边长×边长=×边长×边长,而边长×边长=正方形面积,所以圆盘面积=×正方形面积;连接正方形的对角线,分成4个相同的小三角形,对角线就是圆的直径,也就是2米,小三角的底是对角线的一半,也就是1米,高也是对角线的一半,也是1米,根据三角形的面积=底×高÷2求出一个小三角形的面积,再乘4就是正方形的面积。最后把正方形面积乘即可求出圆盘面积。
【详解】(1)2÷2=1(米)
3.14×1×1=3.14(平方米)
答:这张圆形餐桌的面积是3.14平方米。
(2)3.14×2=6.28(米)
6.28÷0.5=12.56≈12(人)
答:这张圆形餐桌大约坐12人。
(3)2÷2=1(米)
1×1÷2×4=2(平方米)
×2=1.57(平方米)
答:这个转盘有1.57平方米。
10.105平方厘米
【分析】根据平行四边形的面积=底×高,由题意可知,CD×7=BC×10,假设它们的积为1,用1分别除以7和10,再用商列比并化简,可分别得CD和BC的比,根据比的应用,用51除以2再除以CD和BC对应的份数和,得到每份的长度,再用每份长度乘BC对应的份数,得BC的长,再代入面积公式计算即可。
【详解】假设CD×7=BC×10=1
CD∶BC=
(厘米)
(平方厘米)
则平行四边形的面积是105平方厘米。
【点睛】根据等量关系CD×7=BC×10,确定CD和BC的比,转化为比的应用题。
11.2175平方米
【分析】如下图,正方形建筑物的边长是20米,羊被30米长的绳子拴在了正方形建筑物的一个顶点上,那么羊吃草的面积=半径为30米的圆的面积+2个半径为(30-20)米的圆的面积;根据圆的面积公式S=πr2,代入数据计算即可求解。
【详解】3×302×+3×(30-20)2××2
=3×900×+3×102××2
=2025+3×100××2
=2025+150
=2175(平方米)
答:这只羊能吃到草的草地面积是2175平方米。
12.(1)21.5平方厘米
(2)5秒
【分析】(1)重叠时,圆在正方形内,相当于正方形内画一个最大的圆,求没有重合部分的面积,就是用正方形面积-圆的面积;根据正方形面积公式:面积=边长×边长,圆的面积公式:面积=π×半径2,代入数据,即可解答。
(2)把正方形机器人的速度看作单位“1”,圆形机器人的速度是正方形机器人速度的(1+40%),用正方形机器人的速度×(1+40%),求出圆形机器人的速度。求经过多少秒后恰好完全分开,先求出正方形机器人走过的路程与圆形机器人走过的路程和,正方形机器人与圆形机器人相距的距离+正方形机器人的边长的长度+圆形机器人的直径的长度,就是两个机器人完全分开后的路程,再根据时间=路程÷速度,用正方形机器人走过的路程与圆形机器人走过的路程和÷正方形机器人的速度与圆形机器人的速度和,即可解答。
【详解】(1)10×10-3.14×(10÷2)2
=10×10-3.14×52
=100-3.14×25
=100-78.5
=21.5(平方厘米)
答:没有重合部分的面积是21.5平方厘米。
(2)4×(1+40%)
=4×140%
=5.6(厘米)
(28+10+10)÷(4+5.6)
=(38+10)÷9.6
=48÷9.6
=5(秒)
答:经过5秒后恰好完全分开。
【点睛】解答本题的关键是求出正方形机器人与圆形机器人走过的路程。
13.图见详解;1774.96平方米
【分析】如下图,把这个冰球场地分成4个半径为8米的圆、中间是一个长61米、宽(30-8-8)米的长方形、上下是两个完全一样的长为(61-8-8)米、宽为8米的长方形;根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】如图:
3.14×82××4
=3.14×64××4
=200.96(平方米)
61×(30-8-8)
=61×14
=854(平方米)
(61-8-8)×8×2
=45×8×2
=720(平方米)
200.96+854+720
=1054.96+720
=1774.96(平方米)
答:这个冰球比赛场地的使用面积是1774.96平方米。
14.1177.5平方厘米
【分析】这个雨刷刮出的面积等于以40厘米为半径的圆面积的减去以(40-30)厘米为半径的圆面积的,根据圆的面积=×半径的平方,代入数据解答即可。
【详解】40-30=10(厘米)
3.14××-3.14××
=3.14×1600×-3.14×100×
=3.14×400-3.14×25
=1256-78.5
=1177.5(平方厘米)
答:这个雨刷刮出的面积是1177.5平方厘米。
15.39.25平方米;15.7秒
【分析】观察图形可知:比赛场地是一个不规则图形,右下角的小半圆可以填补到左边的空白半圆处,这样比赛场地就变为一个以10米为直径的半圆,根据圆的面积=πr2,求出圆的面积,再除以2即可求出需要草皮的面积。
观察图形可知:比赛场地周长的上半部分是以10米为直径的圆的周长的一半,下半部分的两条半圆弧可以组成以(10÷2)米为直径的圆。根据圆的周长=πd,分别求出两部分的长度,再把它们相加可以求出比赛场地的周长。最后根据路程÷速度=时间,用场地的周长除以2,即可求出沿赛道跑一周需要多长时间。
【详解】(10÷2)2×3.14÷2
=52×3.14÷2
=25×3.14÷2
=39.25(平方米)
10×3.14÷2+10÷2×3.14
=15.7+15.7
=31.4(米)
31.4÷2=15.7(秒)
答:需要准备39.25平方米草皮;沿赛道跑一周需要15.7秒。
16.
25.68平方米
【分析】观察可知,草坪的面积等于半圆面积减三角形面积,已知三角形是直角等腰三角形,两条直角边都等于半圆的半径,根据的逆运算,用三角形面积乘2得到r2,再根据圆的面积公式,圆的面积除以2可得到半圆的面积,代入数据计算即可得解。
【详解】r2=(平方米)
(平方米)
答:草坪的面积是25.68平方米。
17.
5024平方厘米
【分析】雨刷摇摆角度是180°,求雨刷能刷到的面积,就是一个环形面积的一半,环形的,,根据环形的面积公式,用环形的面积再除以2即可得解。
【详解】60-40=20(厘米)
(平方厘米)
答:这种雨刷能刷到的面积是5024平方厘米。
18.(1)62.8厘米;(2)114平方厘米
【分析】(1)看图可知,花瓣的周长是由两个半径是10厘米的四分之一圆的弧长,以及一个半径是(10×2)厘米的四分之一圆的弧长。圆周长=2πr,据此先求出半径是10厘米圆的周长,再除以4乘2,求出两个半径是10厘米的四分之一圆的弧长。再根据圆周长公式求出半径是(10×2)厘米圆的周长,再除以4,求出半径是(10×2)厘米的四分之一圆的弧长。将这两部分相加,即可求出这片“花瓣儿”的周长。
(2)如图:连接大正方形左下角和右上角的顶点,画出一条对角线。根据画好的图可知,这片花瓣在对角线上方的部分是可以剪拼到左下方的。圆面积=πr2,据此求出半径是(10×2)厘米圆的面积。将圆面积除以4,求出四分之一圆的面积。三角形面积=底×高÷2,据此求出三角形的面积。将四分之一圆的面积减去三角形的面积,即可求出花瓣的面积。
【详解】(1)2×3.14×10÷4×2+2×3.14×(10×2)÷4
=2×3.14×10÷4×2+2×3.14×20÷4
=62.8÷4×2+125.6÷4
=31.4+31.4
=62.8(厘米)
答:这片“花瓣儿”的周长是62.8厘米。
(2)如图:
10×2=20(厘米)
3.14×202÷4-20×20÷2
=3.14×400÷4-20×20÷2
=314-200
=114(平方厘米)
答:这片“花瓣儿”的面积是114平方厘米。
19.10.99米
【分析】根据题意,起落杆完成一次升降运动,起落杆A点移动了2个半径为3.5米的圆周长的;根据圆的周长公式C=2πr,代入数据计算求出起落杆A点总共移动的长度。
【详解】2×3.14×3.5××2=10.99(米)
答:这时起落杆A点总共移动了10.99米。
20.3.768米
【分析】观察图形可知,200米赛跑的直道长度一定,但相邻内、外半圆的圆弧长度有差距,所以相邻跑道的起跑线的差距等于相邻内、外半圆的圆弧长度差。
根据圆的周长公式C=2πr可知,半圆弧长=2πr÷2=πr,相邻外半圆与内半圆的圆弧长之差为πR-πr=π(R-r),已知跑道宽为1.2米,即R-r=1.2米,由此得出,200米赛跑相邻跑道的起跑线的差距=π×跑道宽,代入数据计算即可得解。
【详解】3.14×1.2=3.768(米)
答:应让外跑道的运动员前移3.768米。
21.11.61平方厘米
【分析】
如图所示,在一个正方形里面有一个最大的圆,这个圆的直径是这个正方形的边长。可以观察发现正方形减去圆,剩下正方形四个角上一模一样的图形(S1),每一个S1的面积=(正方形的面积-圆的面积)÷4,根据正方形的面积=边长×边长、圆的面积=计算出一个S1的面积;根据各部分之间的关系,可知阴影部分的面积=(正方形的面积-半径是6厘米圆的面积-S1)×2,据此代入数值计算即可。
【详解】6×6=36(平方厘米)
(平方厘米)
S1面积:(36-28.26)÷4
=7.74÷4
=1.935 (平方厘米)
阴影部分面积:(36--1.935)×2
=(36- 28.26-1.935)×2
=5.805×2
=11.61(平方厘米)
答:阴影部分的面积为11.61平方厘米。
【点睛】找出如何得出阴影部分面积的方法,再利用基础图形的公式计算。
22.20厘米;8厘米;160平方厘米
【分析】长方形的周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数=一份数,一份数分别乘长和宽的对应份数,即可求出长和宽,再根据长方形面积=长×宽,即可求出面积。
【详解】56÷2÷(5+2)
=28÷7
=4(厘米)
4×5=20(厘米)
4×2=8(厘米)
20×8=160(平方厘米)
答:这个长方形的长和宽分别是20厘米、8厘米,面积是160平方厘米。
23.6.28厘米;15.74厘米
【分析】由题可知,长方形的面积和圆的面积相等,阴影部分的面积是9.42平方厘米,则阴影部分占整个圆的,用阴影部分的面积除以,求出圆和长方形的面积,又知长方形的宽等于圆的半径,根据圆的面积=πr2,求出圆的半径,再用长方形的面积除以宽,求出长方形的长;阴影部分的周长由四部分组成:圆周长的,长方形的长,长方形的宽以及长方形长与宽之间的差;根据圆的周长=2πr,分别计算出圆周长的、长方形长与宽之间的差,最后将四部分相加,得到阴影部分的周长。
【详解】9.42÷
=9.42×
=12.56(平方厘米)
12.56÷3.14=4
4=2×2
所以圆的半径是2厘米。
12.56÷2=6.28(厘米)
3.14×2×2×
=6.28×2×
=12.56×
=3.14(厘米)
6.28-2=4.28(厘米)
3.14+6.28+2+4.28
=9.42+2+4.28
=11.42+4.28
=15.7(厘米)
答:长方形的长是6.28厘米,阴影部分的周长是15.74厘米。
24.94.2平方厘米
【分析】观察可知,阴影部分的面积就是大正方形与小正方形的面积差,即,根据环形的面积=,代入数据计算即可得解。
【详解】(平方厘米)
答:环形的面积是94.2平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
