第17章勾股定理能力提升卷(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第17章勾股定理能力提升卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.以下列各组数为边长,可以构成直角三角形的是( )
A.2,3,4 B.3,4,5 C.6,8,15 D.5,12,17
2.一个直角三角形的两边长分别为6和8,则斜边长为( )
A.10 B.8 C.或8 D.10或8
3.若直角三角形的两直角边长分别为,,且满足,则该直角三角形的第三边长为( )
A.3 B.4 C. D.5
4.下列命题是假命题的是( )
A.在中,若,则是直角三角形
B.在中,若,则是直角三角形
C.在中,若,则是直角三角形
D.在中,若,则是等腰直角三角形
5.如图,以直角三角形的斜边为边构造正方形,则该正方形的对角线长为( )
A. B. C. D.
6.如图,在数轴上点所对应的数为3,,以为圆心,为半径的圆弧交数轴于点,则点在数轴上所对应的数是( )
A. B. C. D.
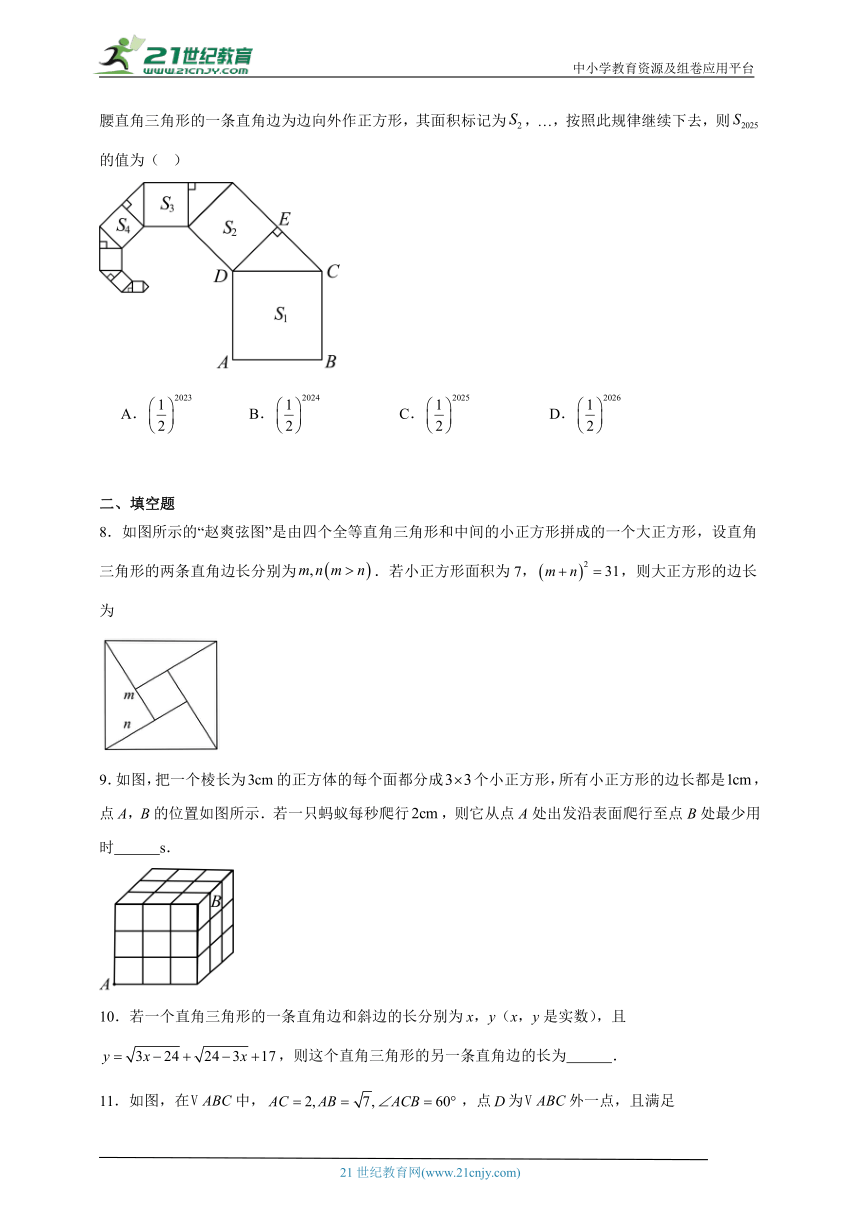
7.如图,正方形的边长为,其面积标记为,以为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为( )
A. B. C. D.
二、填空题
8.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,设直角三角形的两条直角边长分别为.若小正方形面积为7,,则大正方形的边长为
9.如图,把一个棱长为的正方体的每个面都分成个小正方形,所有小正方形的边长都是,点A,B的位置如图所示.若一只蚂蚁每秒爬行,则它从点A处出发沿表面爬行至点B处最少用时 s.
10.若一个直角三角形的一条直角边和斜边的长分别为x,y(x,y是实数),且,则这个直角三角形的另一条直角边的长为 .
11.如图,在中,,点为外一点,且满足,则的长为 .
12.如图,在中,于点,,,,则的面积为 .
13.围棋在我国古代称为“弈”、春秋战国时期、围棋已在社会上广泛流传了.图中截取了围棋棋盘的一部分,若每个小正方形的边长均为1,则两枚棋子之间的距离为 .
14.已知,在内,连接,其中是边长为2的等边三角形,是等腰三角形,则三角形的面积是 .
三、解答题
15.如图,在中,,点,分别是,上的点,连接并延长交的延长线于点.
(1)求证:.
(2)求证:是等腰三角形.
16.如图,台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为、,且,过点作于点,以台风中心为圆心,半径为的圆形区域内为受影响区域,台风的速度为.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.
17.某学校为防止雨天地滑,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,每平方米地毯25元,需要花费多少钱地毯才能铺满所有台阶.(假设地毯在铺的过程中没有损耗)
18.如图,四边形中,点在上,连接、,,,.
(1)求证:;
(2)若,,,求的长.
19.在中,,是的角平分线.
(1)如图①,过点D作交于点G,求证:是等腰三角形.
(2)如图②,若,求的长.
20.已知,在中,,在外取一点P,连接、,使得,,连接,过点A作于点H.
(1)如图1,若,求的度数;
(2)如图2,若点P在边左侧,请写出线段、、三者之间的数量关系,并说明理由;
(3)如图3,若点P在边右侧,,,求的面积.
《第17章勾股定理能力提升卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 B D D A C B D
1.B
【分析】本题考查了勾股定理的逆定理,根据勾股定理的逆定理和三角形三边关系进行计算,逐一判断即可解答.
【详解】解:A.,,
,
不能构成直角三角形,故选项不符合题意;
B.,,
,
能构成直角三角形,故选项不符合题意;
C.,
不能构成三角形,故选项不符合题意;
D.,
不能构成三角形,故选项不符合题意;
故选:B.
2.D
【分析】本题考查了勾股定理、二次根式的化简,熟练掌握勾股定理是解题关键.分两种情况:①当6和8都是直角三角形的直角边长时,利用勾股定理求解即可得;②当6是直角边长,8是斜边长时,利用勾股定理求出另一直角边长,由此即可得.
【详解】解:①当6和8都是直角三角形的直角边长时,斜边长为;
②当6是直角边长,8是斜边长时,另一直角边长为,符合题意;
综上,斜边长为10或8,
故选:D.
3.D
【分析】本题考查了非负数的性质,勾股定理.先根据非负数的性质求出m与n的长,再根据勾股定理计算即可.
【详解】解:由题意得,,,
解得:,,
∵,是直角三角形的两直角边,
∴直角三角形的第三条边长为.
故选D.
4.A
【分析】本题考查了勾股定理的逆定理、平方差公式、等腰三角形的判定、三角形的内角和定理等知识,熟练掌握勾股定理的逆定理是解题关键.根据三角形的内角和定理可得的大小,由此即可判断选项A是假命题;根据勾股定理的逆定理即可判断选项B是真命题;根据三角形的内角和定理可得的大小,由此即可判断选项C是真命题;根据勾股定理的逆定理、等腰三角形的判定即可判断选项D是真命题.
【详解】解:A、若,
∴,,,
∴不是直角三角形,则此项是假命题;
B、若,
∴,即,
∴是直角三角形,则此项是真命题;
C、若,
∴,,,
∴是直角三角形,则此项是真命题;
D、若,
∴设,则,,
∴,且,
∴是等腰直角三角形,则此项是真命题;
故选:A.
5.C
【分析】本题考查的是正方形的性质及勾股定理的应用,掌握勾股定理求解直角三角形的边长是解题的关键.先由勾股定理求解直角三角形的斜边长为,再根据勾股定理求正方形的对角线长即可.
【详解】解:如图,由勾股定理得,直角三角形的斜边长为,
正方形的边长为,
正方形的对角线长为,
故选:C.
6.B
【分析】本题考查了实数与数轴,勾股定理,掌握直角三角形两直角边的平方和等于斜边的平方是解题的关键.
根据勾股定理求出的长度,得到的长度,即可得到点在数轴上所对应的数.
【详解】解:∵,,,
,
,
点在数轴上所对应的数是,
故选:B.
7.D
【分析】本题考查了勾股定理.根据等腰直角三角形的性质结合勾股定理以及三角形的面积公式可得出部分、、、的值,根据面积的变化即可找出变化规律“”,依此规律即可解决问题.
【详解】解:如图所示,
是等腰直角三角形,
,,
,
,
即等腰直角三角形的直角边为斜边的倍,
,
,
,
,
,
,
,
故选:D.
8.
【分析】本题考查了与弦图有关的勾股定理得应用,完全平方公式的应用,根据小正方形面积为7得出,结合,得出,即可得出结果.
【详解】解:∵小正方形面积为7,
∴,
∴
又∵,
∴
∴得,
∴,
∴大正方形的边长为.
故答案为:.
9.
【分析】本题考查了展开与折叠,勾股定理;
分两种情况对正方体进行展开,然后利用勾股定理计算出最短路径,进而可得答案.
【详解】解:分两种情况讨论:
①如图1,展开底面与右面,由勾股定理,得;
②如图2,展开前面与上面,由勾股定理,得.
∵,
∴最短路径长为5cm,
∴这只蚂蚁从点A处出发沿表面爬行至点B处最少用时.
故答案为:.
10.15
【分析】本题考查了二次根式有意义的条件,勾股定理;
根据二次根式有意义的条件得出,求出x,y,再利用勾股定理即可求出这个直角三角形的另一条直角边的长.
【详解】解:根据二次根式有意义可得:且,
∴,
∴,
∴,
∴这个直角三角形的另一条直角边的长为:,
故答案为:.
11.
【分析】此题考查全等三角形的判定与性质、直角三角形、勾股定理.作于点,于点,交的延长线于点,则,先由两条平行线之间的距离处处相等得到,再证明得到,然后在中由求出,,,,再利用得到,接着利用勾股定理依次求出,,,于是得到问题的答案.
【详解】解:作于点,于点,交的延长线于点,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
12.33
【分析】本题考查全等三角形的判定及性质,勾股定理,作平分,过点作,可证,,得,,,在中,,在中,,即,求得,即可求解.
【详解】解:作平分,过点作,
∴,
∵,
∴,
∵,,即,
∴
∴,
同理,
∴,,
∵,
∴在中,,
在中,,即,
解得,
∴,
故答案为:33.
13.
【分析】本题考查勾股定理,利用网格特点找直角三角形即可求解.
【详解】解:如图,,
由勾股定理可得:,
故答案为:.
14.或1或2
【分析】本题考查了等边三角形的性质,等腰三角形的性质及勾股定理的应用,解题的关键是巧妙运用分类讨论思想结合勾股定理解决问题.根据题意可求得的长及,分三种情况讨论:当时,当时,当时,利用勾股定理即可求解.
【详解】解:∵是边长为2的等边三角形,
∴,,则,
当时,过点作,则为等腰直角三角形,
∴,
在中,,即,
∴;
当时,则为等腰直角三角形,
∴,
在中,,即,
∴;
当时,则为等腰直角三角形,
∴;
综上所诉,的面积为或1或2,
故答案为:或1或2.
15.(1)见解析
(2)见解析
【分析】此题考查了勾股定理的逆定理、等腰三角形的判定和性质等知识,熟练掌握勾股定理逆定理是关键.
(1)根据勾股定理的逆定理进行证明即可;
(2)利用等腰三角形的判定和性质、直角三角形两锐角互余、对顶角相等进行证明即可.
【详解】(1)证明:,
.
是直角三角形,.
.
(2),
.
,
.
.
,
.
.
是等腰三角形.
16.(1)监测点A与监测点B之间的距离为
(2)海港C会受到此次台风的影响,台风影响该海港8小时
【分析】本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.
(1)利用勾股定理求出即可;
(2)利用三角形面积得出的长,进而得出海港是否受台风影响;若受影响,利用勾股定理得出以及的长,进而得出台风影响该海港持续的时间.
【详解】(1)解:在中,,,
,
答:监测点与监测点之间的距离为;
(2)解:海港受台风影响,
理由:,,
,
,
,
以台风中心为圆心周围以内为受影响区域,
海港会受到此次台风的影响,
以为圆心,长为半径画弧,交于,,
则时,正好影响港口,
在中,,
,
台风的速度为,
.
答:台风影响该海港持续的时间为8小时.
17.(1)的长为;
(2)元
【分析】本题考查了勾股定理的应用,利用勾股定理求出的长度是解题的关键.
(1)由勾股定理列式计算即可;
(2)由长方形面积公式计算即可.
【详解】(1)解:∵,,,
,
答:的长为;
(2)解:地毯长为:,
∴地毯的面积为,
每平方米地毯25元,
需要花费(元);
答:需要花费元地毯才能铺满所有台阶.
18.(1)证明见解析
(2)
【分析】本题主要考查全等三角形的判定和性质,勾股定理,掌握全等三角形的判定方法是解题的关键.
(1)根据角的和与差得,然后利用即可证明结论;
(2)根据全等三角形的性质得,,然后利用勾股定理求得,然后利用线段的和差即可解答.
【详解】(1)证明:,
,
,
在和中
;
(2)解:
,
,
中,
.
19.(1)见解析
(2)3
【分析】(1)先根据是的角平分线得出,再由得出,据此得出结论;
(2)先根据勾股定理求出的长,过点D作于点E,由角平分线的性质得出,故可得出,再次运用勾股定理即可得到答案.
【详解】(1)证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴,
即是等腰三角形;
(2)解:∵,,,
∴,
过点D作于点E,
∵是的角平分线.
∴,
在与中,
,
∴,
∴,
设,则,,,
在中,,即,
解得,
∴.
【点睛】本题考查的是勾股定理,角平分线的定义,角平分线的性质,平行线的性质,全等三角形的判定与性质,熟知以上知识是解题的关键.
20.(1)
(2),理由见解析
(3)
【分析】(1)设,则,得到,结合等腰三角形性质得到,,再利用三角形内角和定理建立方程求解,即可解题;
(2)在上取,记与交于点,结合等腰三角形性质证明,作于点,利用全等三角形性质,以及三角形外角性质进而证明,再结合全等三角形性质求解,即可解题.
(3)在上取,由(2)同理可证,,利用全等三角形性质,以及等腰三角形性质得到,结合勾股定理逆定理推出,再利用等腰直角三角形性质得到为与的交点,作,延长交于点,进而证明,结合全等三角形性质得到,进而得到,最后利用三角形面积公式求解,即可解题.
【详解】(1)解:,
设,则,
,
,
,
,
,
,
,
解得,
的度数为;
(2)解:,理由如下:
在上取,记与交于点,
,,
,
,,
,
,,
作于点,
,,
,
于点H,
,
,
,
,,
,
;
(3)解:在上取,
由(2)同理可证,,
,,
于点H, ,
,
,,
,
,
,
,
,
,
,
为与的交点,
,
,
作,延长交于点,
,,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形性质和判定,三角形内角和定理,全等三角形性质和判定,三角形外角性质,平行线性质,勾股定理逆定理,解题的关键在于作辅助线构造全等三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第17章勾股定理能力提升卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.以下列各组数为边长,可以构成直角三角形的是( )
A.2,3,4 B.3,4,5 C.6,8,15 D.5,12,17
2.一个直角三角形的两边长分别为6和8,则斜边长为( )
A.10 B.8 C.或8 D.10或8
3.若直角三角形的两直角边长分别为,,且满足,则该直角三角形的第三边长为( )
A.3 B.4 C. D.5
4.下列命题是假命题的是( )
A.在中,若,则是直角三角形
B.在中,若,则是直角三角形
C.在中,若,则是直角三角形
D.在中,若,则是等腰直角三角形
5.如图,以直角三角形的斜边为边构造正方形,则该正方形的对角线长为( )
A. B. C. D.
6.如图,在数轴上点所对应的数为3,,以为圆心,为半径的圆弧交数轴于点,则点在数轴上所对应的数是( )
A. B. C. D.
7.如图,正方形的边长为,其面积标记为,以为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为( )
A. B. C. D.
二、填空题
8.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,设直角三角形的两条直角边长分别为.若小正方形面积为7,,则大正方形的边长为
9.如图,把一个棱长为的正方体的每个面都分成个小正方形,所有小正方形的边长都是,点A,B的位置如图所示.若一只蚂蚁每秒爬行,则它从点A处出发沿表面爬行至点B处最少用时 s.
10.若一个直角三角形的一条直角边和斜边的长分别为x,y(x,y是实数),且,则这个直角三角形的另一条直角边的长为 .
11.如图,在中,,点为外一点,且满足,则的长为 .
12.如图,在中,于点,,,,则的面积为 .
13.围棋在我国古代称为“弈”、春秋战国时期、围棋已在社会上广泛流传了.图中截取了围棋棋盘的一部分,若每个小正方形的边长均为1,则两枚棋子之间的距离为 .
14.已知,在内,连接,其中是边长为2的等边三角形,是等腰三角形,则三角形的面积是 .
三、解答题
15.如图,在中,,点,分别是,上的点,连接并延长交的延长线于点.
(1)求证:.
(2)求证:是等腰三角形.
16.如图,台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为、,且,过点作于点,以台风中心为圆心,半径为的圆形区域内为受影响区域,台风的速度为.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.
17.某学校为防止雨天地滑,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,每平方米地毯25元,需要花费多少钱地毯才能铺满所有台阶.(假设地毯在铺的过程中没有损耗)
18.如图,四边形中,点在上,连接、,,,.
(1)求证:;
(2)若,,,求的长.
19.在中,,是的角平分线.
(1)如图①,过点D作交于点G,求证:是等腰三角形.
(2)如图②,若,求的长.
20.已知,在中,,在外取一点P,连接、,使得,,连接,过点A作于点H.
(1)如图1,若,求的度数;
(2)如图2,若点P在边左侧,请写出线段、、三者之间的数量关系,并说明理由;
(3)如图3,若点P在边右侧,,,求的面积.
《第17章勾股定理能力提升卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7
答案 B D D A C B D
1.B
【分析】本题考查了勾股定理的逆定理,根据勾股定理的逆定理和三角形三边关系进行计算,逐一判断即可解答.
【详解】解:A.,,
,
不能构成直角三角形,故选项不符合题意;
B.,,
,
能构成直角三角形,故选项不符合题意;
C.,
不能构成三角形,故选项不符合题意;
D.,
不能构成三角形,故选项不符合题意;
故选:B.
2.D
【分析】本题考查了勾股定理、二次根式的化简,熟练掌握勾股定理是解题关键.分两种情况:①当6和8都是直角三角形的直角边长时,利用勾股定理求解即可得;②当6是直角边长,8是斜边长时,利用勾股定理求出另一直角边长,由此即可得.
【详解】解:①当6和8都是直角三角形的直角边长时,斜边长为;
②当6是直角边长,8是斜边长时,另一直角边长为,符合题意;
综上,斜边长为10或8,
故选:D.
3.D
【分析】本题考查了非负数的性质,勾股定理.先根据非负数的性质求出m与n的长,再根据勾股定理计算即可.
【详解】解:由题意得,,,
解得:,,
∵,是直角三角形的两直角边,
∴直角三角形的第三条边长为.
故选D.
4.A
【分析】本题考查了勾股定理的逆定理、平方差公式、等腰三角形的判定、三角形的内角和定理等知识,熟练掌握勾股定理的逆定理是解题关键.根据三角形的内角和定理可得的大小,由此即可判断选项A是假命题;根据勾股定理的逆定理即可判断选项B是真命题;根据三角形的内角和定理可得的大小,由此即可判断选项C是真命题;根据勾股定理的逆定理、等腰三角形的判定即可判断选项D是真命题.
【详解】解:A、若,
∴,,,
∴不是直角三角形,则此项是假命题;
B、若,
∴,即,
∴是直角三角形,则此项是真命题;
C、若,
∴,,,
∴是直角三角形,则此项是真命题;
D、若,
∴设,则,,
∴,且,
∴是等腰直角三角形,则此项是真命题;
故选:A.
5.C
【分析】本题考查的是正方形的性质及勾股定理的应用,掌握勾股定理求解直角三角形的边长是解题的关键.先由勾股定理求解直角三角形的斜边长为,再根据勾股定理求正方形的对角线长即可.
【详解】解:如图,由勾股定理得,直角三角形的斜边长为,
正方形的边长为,
正方形的对角线长为,
故选:C.
6.B
【分析】本题考查了实数与数轴,勾股定理,掌握直角三角形两直角边的平方和等于斜边的平方是解题的关键.
根据勾股定理求出的长度,得到的长度,即可得到点在数轴上所对应的数.
【详解】解:∵,,,
,
,
点在数轴上所对应的数是,
故选:B.
7.D
【分析】本题考查了勾股定理.根据等腰直角三角形的性质结合勾股定理以及三角形的面积公式可得出部分、、、的值,根据面积的变化即可找出变化规律“”,依此规律即可解决问题.
【详解】解:如图所示,
是等腰直角三角形,
,,
,
,
即等腰直角三角形的直角边为斜边的倍,
,
,
,
,
,
,
,
故选:D.
8.
【分析】本题考查了与弦图有关的勾股定理得应用,完全平方公式的应用,根据小正方形面积为7得出,结合,得出,即可得出结果.
【详解】解:∵小正方形面积为7,
∴,
∴
又∵,
∴
∴得,
∴,
∴大正方形的边长为.
故答案为:.
9.
【分析】本题考查了展开与折叠,勾股定理;
分两种情况对正方体进行展开,然后利用勾股定理计算出最短路径,进而可得答案.
【详解】解:分两种情况讨论:
①如图1,展开底面与右面,由勾股定理,得;
②如图2,展开前面与上面,由勾股定理,得.
∵,
∴最短路径长为5cm,
∴这只蚂蚁从点A处出发沿表面爬行至点B处最少用时.
故答案为:.
10.15
【分析】本题考查了二次根式有意义的条件,勾股定理;
根据二次根式有意义的条件得出,求出x,y,再利用勾股定理即可求出这个直角三角形的另一条直角边的长.
【详解】解:根据二次根式有意义可得:且,
∴,
∴,
∴,
∴这个直角三角形的另一条直角边的长为:,
故答案为:.
11.
【分析】此题考查全等三角形的判定与性质、直角三角形、勾股定理.作于点,于点,交的延长线于点,则,先由两条平行线之间的距离处处相等得到,再证明得到,然后在中由求出,,,,再利用得到,接着利用勾股定理依次求出,,,于是得到问题的答案.
【详解】解:作于点,于点,交的延长线于点,则,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
12.33
【分析】本题考查全等三角形的判定及性质,勾股定理,作平分,过点作,可证,,得,,,在中,,在中,,即,求得,即可求解.
【详解】解:作平分,过点作,
∴,
∵,
∴,
∵,,即,
∴
∴,
同理,
∴,,
∵,
∴在中,,
在中,,即,
解得,
∴,
故答案为:33.
13.
【分析】本题考查勾股定理,利用网格特点找直角三角形即可求解.
【详解】解:如图,,
由勾股定理可得:,
故答案为:.
14.或1或2
【分析】本题考查了等边三角形的性质,等腰三角形的性质及勾股定理的应用,解题的关键是巧妙运用分类讨论思想结合勾股定理解决问题.根据题意可求得的长及,分三种情况讨论:当时,当时,当时,利用勾股定理即可求解.
【详解】解:∵是边长为2的等边三角形,
∴,,则,
当时,过点作,则为等腰直角三角形,
∴,
在中,,即,
∴;
当时,则为等腰直角三角形,
∴,
在中,,即,
∴;
当时,则为等腰直角三角形,
∴;
综上所诉,的面积为或1或2,
故答案为:或1或2.
15.(1)见解析
(2)见解析
【分析】此题考查了勾股定理的逆定理、等腰三角形的判定和性质等知识,熟练掌握勾股定理逆定理是关键.
(1)根据勾股定理的逆定理进行证明即可;
(2)利用等腰三角形的判定和性质、直角三角形两锐角互余、对顶角相等进行证明即可.
【详解】(1)证明:,
.
是直角三角形,.
.
(2),
.
,
.
.
,
.
.
是等腰三角形.
16.(1)监测点A与监测点B之间的距离为
(2)海港C会受到此次台风的影响,台风影响该海港8小时
【分析】本题考查的是勾股定理在实际生活中的运用,解答此类题目的关键是构造出直角三角形,再利用勾股定理解答.
(1)利用勾股定理求出即可;
(2)利用三角形面积得出的长,进而得出海港是否受台风影响;若受影响,利用勾股定理得出以及的长,进而得出台风影响该海港持续的时间.
【详解】(1)解:在中,,,
,
答:监测点与监测点之间的距离为;
(2)解:海港受台风影响,
理由:,,
,
,
,
以台风中心为圆心周围以内为受影响区域,
海港会受到此次台风的影响,
以为圆心,长为半径画弧,交于,,
则时,正好影响港口,
在中,,
,
台风的速度为,
.
答:台风影响该海港持续的时间为8小时.
17.(1)的长为;
(2)元
【分析】本题考查了勾股定理的应用,利用勾股定理求出的长度是解题的关键.
(1)由勾股定理列式计算即可;
(2)由长方形面积公式计算即可.
【详解】(1)解:∵,,,
,
答:的长为;
(2)解:地毯长为:,
∴地毯的面积为,
每平方米地毯25元,
需要花费(元);
答:需要花费元地毯才能铺满所有台阶.
18.(1)证明见解析
(2)
【分析】本题主要考查全等三角形的判定和性质,勾股定理,掌握全等三角形的判定方法是解题的关键.
(1)根据角的和与差得,然后利用即可证明结论;
(2)根据全等三角形的性质得,,然后利用勾股定理求得,然后利用线段的和差即可解答.
【详解】(1)证明:,
,
,
在和中
;
(2)解:
,
,
中,
.
19.(1)见解析
(2)3
【分析】(1)先根据是的角平分线得出,再由得出,据此得出结论;
(2)先根据勾股定理求出的长,过点D作于点E,由角平分线的性质得出,故可得出,再次运用勾股定理即可得到答案.
【详解】(1)证明:∵是的角平分线,
∴,
∵,
∴,
∴,
∴,
即是等腰三角形;
(2)解:∵,,,
∴,
过点D作于点E,
∵是的角平分线.
∴,
在与中,
,
∴,
∴,
设,则,,,
在中,,即,
解得,
∴.
【点睛】本题考查的是勾股定理,角平分线的定义,角平分线的性质,平行线的性质,全等三角形的判定与性质,熟知以上知识是解题的关键.
20.(1)
(2),理由见解析
(3)
【分析】(1)设,则,得到,结合等腰三角形性质得到,,再利用三角形内角和定理建立方程求解,即可解题;
(2)在上取,记与交于点,结合等腰三角形性质证明,作于点,利用全等三角形性质,以及三角形外角性质进而证明,再结合全等三角形性质求解,即可解题.
(3)在上取,由(2)同理可证,,利用全等三角形性质,以及等腰三角形性质得到,结合勾股定理逆定理推出,再利用等腰直角三角形性质得到为与的交点,作,延长交于点,进而证明,结合全等三角形性质得到,进而得到,最后利用三角形面积公式求解,即可解题.
【详解】(1)解:,
设,则,
,
,
,
,
,
,
,
解得,
的度数为;
(2)解:,理由如下:
在上取,记与交于点,
,,
,
,,
,
,,
作于点,
,,
,
于点H,
,
,
,
,,
,
;
(3)解:在上取,
由(2)同理可证,,
,,
于点H, ,
,
,,
,
,
,
,
,
,
,
为与的交点,
,
,
作,延长交于点,
,,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形性质和判定,三角形内角和定理,全等三角形性质和判定,三角形外角性质,平行线性质,勾股定理逆定理,解题的关键在于作辅助线构造全等三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
