第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版(含解析)
文档属性
| 名称 | 第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 17:47:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一次函数的图象经过第一、二、四象限,则( )
A. B. C. D.
2.已知点,都在直线上,则与的大小关系为( )
A. B. C. D.无法确定
3.小王的妈妈即将出国旅行.出发前,小王帮妈妈查询了当地的气温,抵达目的地当日气温是华氏度()我国常用的摄氏温标.和华氏温标满足一次函数关系:,那么小王应建议妈妈抵达目的地时穿( )
A.春季服装 B.夏季服装 C.秋季服装 D.冬季服装
4.温度是影响声音传播速度的一个关键因素.在大多数情况下,随着温度的升高,声速会增大.根据实验测量和理论计算可知,声音在淡水中的传播速度与温度之间满足一次函数关系,部分数据如下表所示,则v与t之间的函数关系式为( )
温度 20 25 30
声速 1480 1505 1530
A. B. C. D.
5.在平面直角坐标系中,一次函数的图象与两坐标轴所围成的三角形的面积为( )
A. B. C. D.
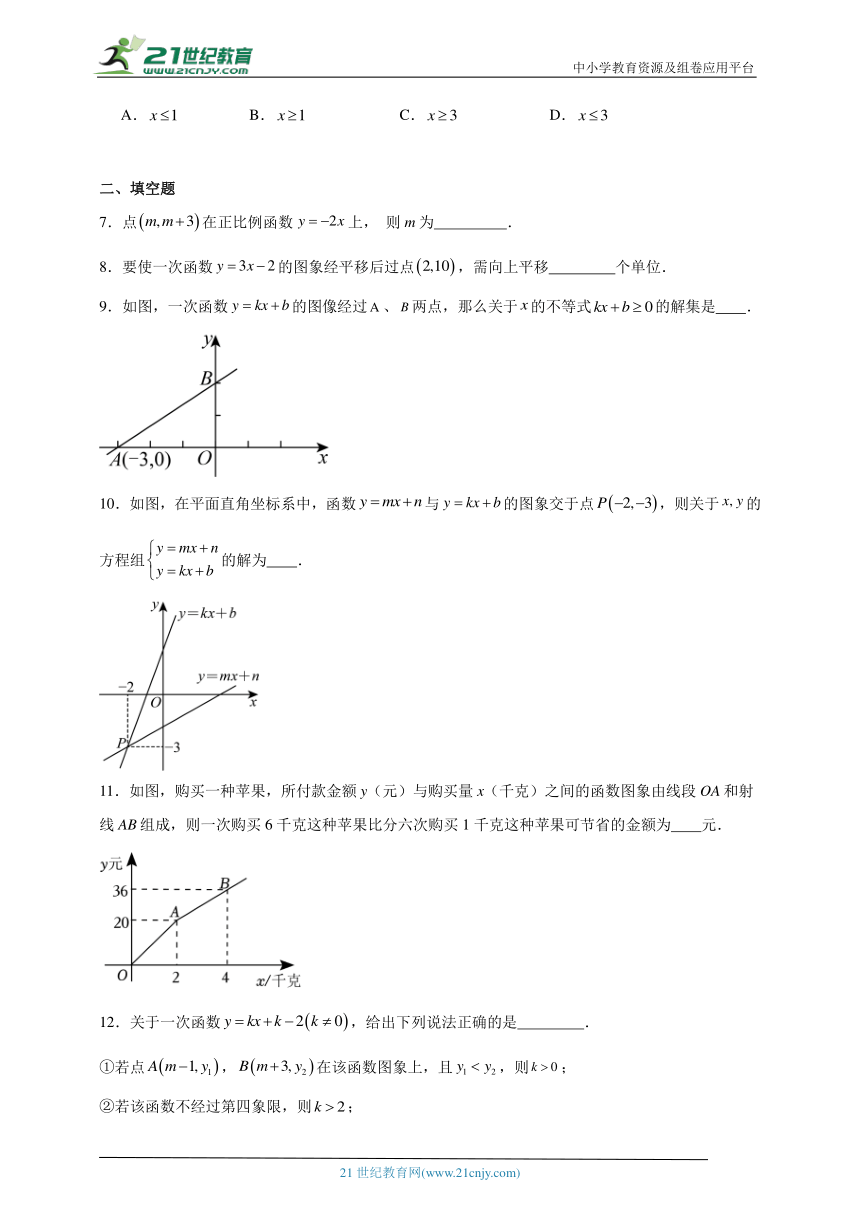
6.如图,在平面直角坐标系中,若直线与直线相交于点P,则不等式的解集是( )
A. B. C. D.
二、填空题
7.点在正比例函数上, 则m为 .
8.要使一次函数的图象经平移后过点,需向上平移 个单位.
9.如图,一次函数的图像经过、两点,那么关于的不等式的解集是 .
10.如图,在平面直角坐标系中,函数与的图象交于点,则关于的方程组的解为 .
11.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为 元.
12.关于一次函数,给出下列说法正确的是 .
①若点,在该函数图象上,且,则;
②若该函数不经过第四象限,则;
③该函数可以看成正比例函数先向左平移一个单位,再向下平移2个单位得到:
④该函数恒过定点.
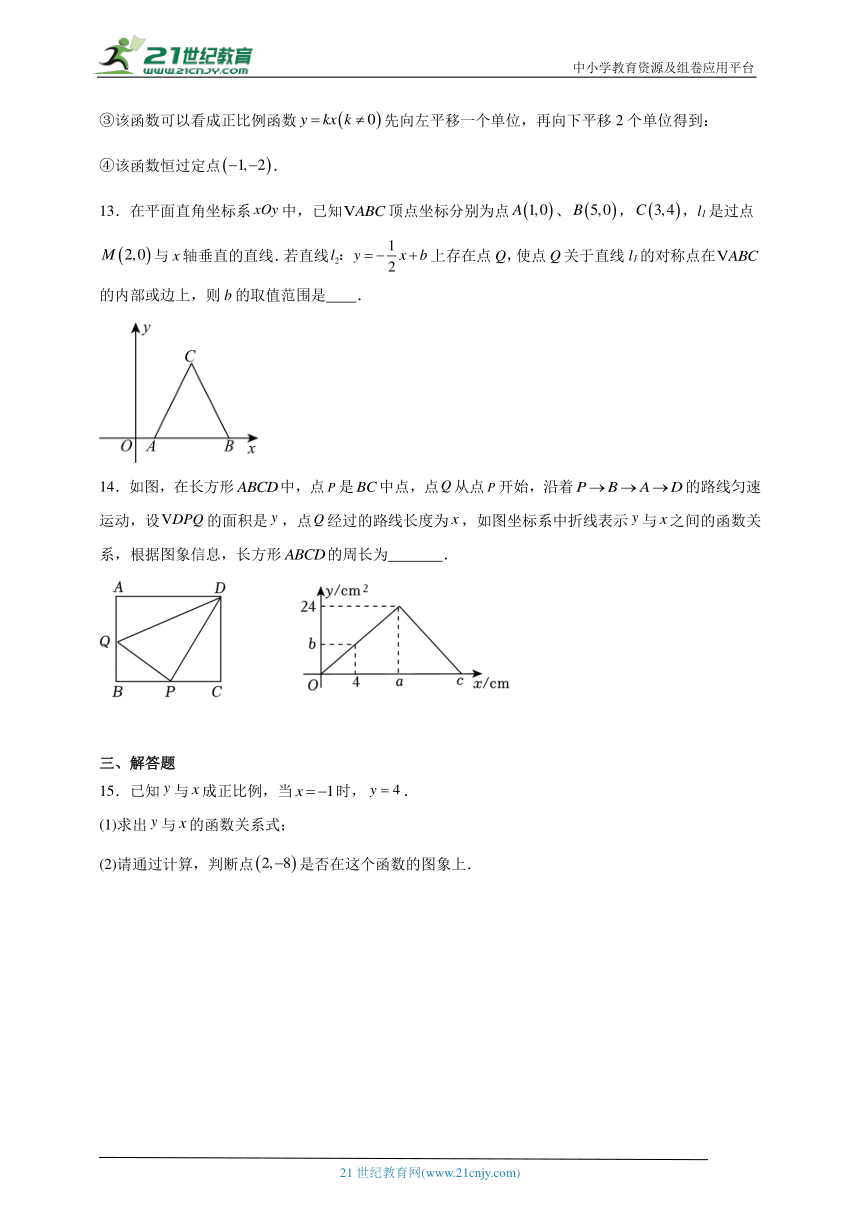
13.在平面直角坐标系中,已知顶点坐标分别为点、,,l1是过点与x轴垂直的直线.若直线上存在点Q,使点Q关于直线l1的对称点在的内部或边上,则b的取值范围是 .
14.如图,在长方形中,点是中点,点从点开始,沿着的路线匀速运动,设的面积是,点经过的路线长度为,如图坐标系中折线表示与之间的函数关系,根据图象信息,长方形的周长为 .
三、解答题
15.已知与成正比例,当时,.
(1)求出与的函数关系式;
(2)请通过计算,判断点是否在这个函数的图象上.
16.如图,在平面直角坐标系中,直线的函数表达式为,直线的函数表达式为
(1)若直线与直线有交点,求的面积;
(2)在(1)的条件下,y轴上是否存在点P,使得的面积与的面积相等?若存在,请求出点P的坐标;若不存在,请说明理由.
17.《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:A款哪吒玩偶的进货单价比B款哪吒玩偶少5元,花500元购进A款哪吒玩偶的数量与花750元购进B款哪吒玩偶的数量相同.
(1)问: A、B两款的进货单价分别是多少元?
(2)小洋决定将A款玩偶的销售单价定为12元,将B款玩偶的销售单价定为20元,小洋打算要花费1000元购进A、B两款玩偶若干个,且A款的数量不小于B款的一半,请你根据计算说明,当A、B两款各购进多少时,小洋获得的总利润最高,最高为多少?
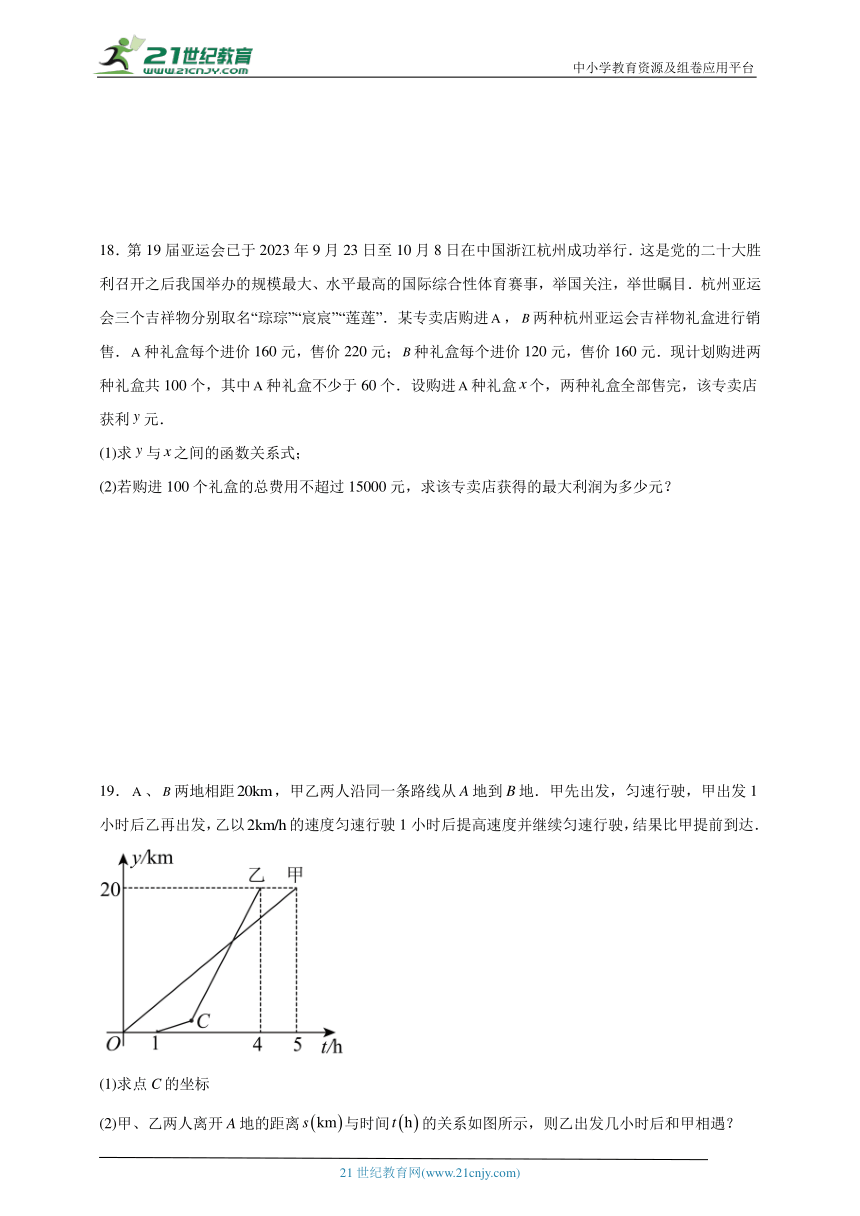
18.第19届亚运会已于2023年9月23日至10月8日在中国浙江杭州成功举行.这是党的二十大胜利召开之后我国举办的规模最大、水平最高的国际综合性体育赛事,举国关注,举世瞩目.杭州亚运会三个吉祥物分别取名“琮琮”“宸宸”“莲莲”.某专卖店购进,两种杭州亚运会吉祥物礼盒进行销售.种礼盒每个进价160元,售价220元;种礼盒每个进价120元,售价160元.现计划购进两种礼盒共100个,其中种礼盒不少于60个.设购进种礼盒个,两种礼盒全部售完,该专卖店获利元.
(1)求与之间的函数关系式;
(2)若购进100个礼盒的总费用不超过15000元,求该专卖店获得的最大利润为多少元?
19.、两地相距,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.
(1)求点C的坐标
(2)甲、乙两人离开A地的距离与时间的关系如图所示,则乙出发几小时后和甲相遇?
20.如图1,在同一平面直角坐标系中,直线与直线相交于点,与轴交于点,直线与轴交于点.
(1)填空: ___________, ___________, ___________;
(2)如图2,点为线段上一动点,将沿直线翻折得到,线段交轴于点.
①当点落在轴上时,求点的坐标;
②若为直角三角形,求点的坐标.
《第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 D B D D D B
1.D
【分析】本题考查了一次函数图象与系数的关系,牢记“的图象在一、二、四象限”是解题的关键.
根据一次函数图象和性质进行判断即可.
【详解】解:∵一次函数的图象经过第一、二、四象限,
∴.
故选:D.
2.B
【分析】本题考查的是一次函数图象上点的坐标特点,分别把点,代入直线,求出,的值,再比较大小即可.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
【详解】解:点,都在直线上,
,.
,
.
故选:B.
3.D
【分析】本题考查了一次函数的应用,代入,,求得抵达目的地时的摄氏温度范围是解题的关键.
【详解】解:当时,,解得:,
当时,,解得:,
即:抵达目的地时的摄氏温度范围是.
这个温度范围比较低,属于冬季的温度范围,所以小王应建议妈妈抵达目的地时穿冬季服装,
故选:D.
4.D
【分析】本题考查了一次函数的应用,熟练掌握待定系数法是解题关键.根据点和,利用待定系数法求解即可得.
【详解】解:设与之间的函数关系式为,
将点和代入得:,
解得,
则与之间的函数关系式为,
故选:D.
5.D
【分析】本题考查了一次函数与坐标轴的交点,几何图形面积的计算,掌握一次函数图象的性质是解题的关键.
根据一次函数图象与坐标轴的交点,几何图形面积的计算公式计算即可.
【详解】解:一次函数,当时,,当时,,
∴,
故选:D .
6.B
【分析】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线在x轴上(或下)方部分所有的点的横坐标所构成的集合.观察函数图象得到当时,函数的图象都在的图象下方,所以不等式的解集为.
【详解】解:当时,函数的图象都在的图象下方,
所以不等式的解集为.
故选:B.
7.
【分析】此题考查了正比例的性质,把点的坐标代入即可求出答案.
【详解】解:∵点在正比例函数上,
∴
解得,
故答案为:
8.
【分析】本题考查的是一次函数图象的平移,利用待定系数法求解一次函数的解析式,掌握一次函数的平移规律是解题的关键.由直线向上平移个单位,其图象经过点,把代入平移后的解析式:即可得到答案.
【详解】解:设直线向上平移个单位,其图象经过点,
点在的图象上,
,
,
故答案为:
9.
【分析】本题考查了一次函数与一元一次不等式,根据函数图象即可得解,采用数形结合的思想是解此题的关键.
【详解】解:由图象可得,关于的不等式的解集是,
故答案为:.
10.
【分析】本题考查了两直线交点求二元一次方程组的解,理解两直线交点的含义是解题的关键.
根据两直线交点得到对应二元一次方程组的解即可.
【详解】解:∵函数与的图象交于点,
∴关于的方程组的解为,
故答案为: .
11.8
【分析】观察函数图象找出点的坐标,利用待定系数法求出线段和设的函数关系式,比较y值大小即可.
【详解】解:设y关于x的函数关系式为,
当时,将代入中得:
,
解得:,
∴;
当时,将代入中得:
,
解得:,
∴;
当时,,
当时,,
(元).
故答案为:8.
【点睛】本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,观察函数图象找出点的坐标,利用待定系数法求出线段和射线的函数关系式是解题的关键.
12.①③④
【分析】本题考查一次函数的定义、一次函数的图象与性质.根据一次函数的相关性质逐项分析求解即可.
【详解】解:若点,在该函数图象上,且,
,
y随x的增大而增大,则,说法正确,故①符合题意;
若该函数不经过第四象限,则,
,原说法错误,故②不符合题意;
正比例函数先向左平移一个单位,再向下平移2个单位得到,即,说法正确,故③符合题意;
令,则该函数恒过定点,说法正确,故④符合题意;
故符合题意的有①③④,
故答案为:①③④.
13.
【分析】本题考查了一次函数图象与系数的关系,一次函数图象上点的坐标特征,坐标与图形变化—对称,数形结合是解题的关键.
求得直线经过点关于直线的对称点时的的值,求得直线经过点关于直线的对称点时的的值,结合图形即可求解.
【详解】解:∵点,是过点与x轴垂直的直线,
∴关于直线的对称点为关于直线的对称点为,
如图,当经过点时,则,
解得,
当直线经过点时,则,解得,
故由图形可知,若直线上存在点,使点关于直线的对称点在的内部或边上,
则的取值范围是.
故答案为:.
14.
【分析】本题考查了根据函数图象获取信息,理解点的运动,函数图象中点的含义是解题的关键.
根据点的运动,函数图形的信息可得,当点运动到点时,,即,则,当点从点运动到点时,的面积是,可得,根据长方形的周长计算公式即可求解.
【详解】解:点是中点,点从点开始,沿着的路线匀速运动,
当点运动到点时,,即,
∴,
∴,
当点从点运动到点时,的面积是,
∴,
解得,,
∴长方形的周长为,
故答案为: .
15.(1)
(2)点在函数的图象上
【分析】本题考查了待定系数法求正比例函数解析式,也考查了正比例函数的性质.
(1)根据成正比例的定义,设,然后把已知的一组对应值代入求出k,从而得到y与x的函数关系式;
(2)利用(1)中的解析式,计算自变量为2对应的函数值,若函数值等于,则可判断点在这个函数的图象上.
【详解】(1)解:设,
把,代入得,
解得,
∴;
(2)解:∵时,,
∴点在函数的图象上.
16.(1)
(2)存在,点P的坐标为或
【分析】此题主要考查了一次函数的图象和性质,三角形的面积,熟练掌握待定系数法求一次函数的解析式,三角形的面积公式是解决问题的关键.
过点C作于点E,于点D,将点代入得,则直线的表达式为,进而可求出点,点,则,,再根据点得,,据此可得的面积;
先求出,设点P的坐标为,则,进而得,进而得,由此解出或,则点P的坐标为或
【详解】(1)解:过点C作于点E,于点D,如图所示:
线与直线有交点,
,
解得:,
直线的表达式为:,
对于,当时,,
当时,,解得:,
点,点,
,,
点,
,
;
(2)存在.
,,
,
点P在y轴上,
设点P的坐标为,
,
,
当的面积与的面积相等时,
,
,
或,
点P的坐标为或,
即当点的坐标为或时,的面积与的面积相等.
17.(1)A款的进货单价是10元,则B款的进货单价是15元
(2)购进A款25个,购进B款50个时,获得的总利润最高,最高为300元
【分析】本题考查分式方程的应用、一元一次不等式的应用、一次函数的应用,理解题意是解答的关键.
(1)设A款的进货单价是元,则B款的进货单价是元,根据题意列分式方程求解即可;
(2)设购进B款个,先根据“A款的数量不小于B款的一半”求得;再设总利润为,则,然后利用一次函数的性质求解即可.
【详解】(1)解:设A款的进货单价是元,则B款的进货单价是元,
根据题意,可得,
解得,
经检验,是该方程的解,
∴,
答:A款的进货单价是10元,则B款的进货单价是15元;
(2)解:设购进B款个,则购进A款个,
又A款的数量不小于B款的一半,
,
解得:,
设总利润为,则,
,
∴随的增大而增大,
当取得最大整数解50时,取得最大值,最大值为,
此时,则,
答:购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
18.(1)
(2)5500元
【分析】本题考查了一次函数的应用,一元一次不等式组的应用.
(1)根据利润等于单件利润乘以数量建立函数关系式即可;
(2)先求出自变量的取值范围,再根据一次函数增减性求最值.
【详解】(1)解:由题知,
与的函数表达式为.
(2)解:由题知
由(1)知
,
随的增大而增大,
当时,有最大值,(元).
19.(1)
(2)
【分析】(1)由题意得,点C的横坐标为,点C的纵坐标为,由此即可得出点C的坐标;
(2)设甲离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得;由“乙以的速度匀速行驶1小时后提高速度并继续匀速行驶”可知,乙的速度在和内是不同的,需要分别求解:设内乙离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得内函数解析式为,设内乙离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得内函数解析式为,综上所述,;依题意,联立方程组,得,解方程组即可求出的值,进而可求出乙出发几小时后和甲相遇.
【详解】(1)解:由题意得:
点C的横坐标为:,
点C的纵坐标为:,
点C的坐标为;
(2)解:设甲离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
,
乙以的速度匀速行驶1小时后提高速度并继续匀速行驶,
乙的速度在和内是不同的,需要分别求解,
设内乙离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
内函数解析式为,
设内乙离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
内函数解析式为,
综上所述,,
依题意,联立方程组,得:
,
解得:,
,
答:乙出发小时后和甲相遇.
【点睛】本题主要考查了一次函数的实际应用(行程问题),求一次函数解析式,两直线的交点与二元一次方程组的解,写出直角坐标系中点的坐标,从函数的图象获取信息,解二元一次方程组等知识点,能够从函数图象中获取正确信息并熟练掌握待定系数法求一次函数解析式是解题的关键.
20.(1),,
(2)①;②或
【分析】(1)把代入,求出,得直线,再把代入,求出,得点的坐标,最后把代入,求出;
(2)①过点作轴于点,作轴于点,求出,再求出,可得,即可得答案;②分两种情况讨论,当时,求出,得,得,得点坐标;当时,设,则,由勾股定理得:,求出,得点坐标.
【详解】(1)解:把代入得:,
解得:,
直线,
把代入得:
解得:,
,
把代入得:,
解得:.
故答案为:,,;
(2)①由(1)知直线,
令,则,
解得:
点,
如图,过点作轴于点,作轴于点,则,,
,
,
,
点的坐标为;
②如下图,
当时,由翻折得:,
,
,
,
,
点的坐标为;
如下图,
当时,,
设,则,
在中,由勾股定理得:,即,
解得:,
,
点的坐标为,
综上,点的坐标为或.
【点睛】此题考查了一次函数,勾股定理,等腰直角三角形的判定与性质,翻折的性质,解题的关键是作辅助线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一次函数的图象经过第一、二、四象限,则( )
A. B. C. D.
2.已知点,都在直线上,则与的大小关系为( )
A. B. C. D.无法确定
3.小王的妈妈即将出国旅行.出发前,小王帮妈妈查询了当地的气温,抵达目的地当日气温是华氏度()我国常用的摄氏温标.和华氏温标满足一次函数关系:,那么小王应建议妈妈抵达目的地时穿( )
A.春季服装 B.夏季服装 C.秋季服装 D.冬季服装
4.温度是影响声音传播速度的一个关键因素.在大多数情况下,随着温度的升高,声速会增大.根据实验测量和理论计算可知,声音在淡水中的传播速度与温度之间满足一次函数关系,部分数据如下表所示,则v与t之间的函数关系式为( )
温度 20 25 30
声速 1480 1505 1530
A. B. C. D.
5.在平面直角坐标系中,一次函数的图象与两坐标轴所围成的三角形的面积为( )
A. B. C. D.
6.如图,在平面直角坐标系中,若直线与直线相交于点P,则不等式的解集是( )
A. B. C. D.
二、填空题
7.点在正比例函数上, 则m为 .
8.要使一次函数的图象经平移后过点,需向上平移 个单位.
9.如图,一次函数的图像经过、两点,那么关于的不等式的解集是 .
10.如图,在平面直角坐标系中,函数与的图象交于点,则关于的方程组的解为 .
11.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买6千克这种苹果比分六次购买1千克这种苹果可节省的金额为 元.
12.关于一次函数,给出下列说法正确的是 .
①若点,在该函数图象上,且,则;
②若该函数不经过第四象限,则;
③该函数可以看成正比例函数先向左平移一个单位,再向下平移2个单位得到:
④该函数恒过定点.
13.在平面直角坐标系中,已知顶点坐标分别为点、,,l1是过点与x轴垂直的直线.若直线上存在点Q,使点Q关于直线l1的对称点在的内部或边上,则b的取值范围是 .
14.如图,在长方形中,点是中点,点从点开始,沿着的路线匀速运动,设的面积是,点经过的路线长度为,如图坐标系中折线表示与之间的函数关系,根据图象信息,长方形的周长为 .
三、解答题
15.已知与成正比例,当时,.
(1)求出与的函数关系式;
(2)请通过计算,判断点是否在这个函数的图象上.
16.如图,在平面直角坐标系中,直线的函数表达式为,直线的函数表达式为
(1)若直线与直线有交点,求的面积;
(2)在(1)的条件下,y轴上是否存在点P,使得的面积与的面积相等?若存在,请求出点P的坐标;若不存在,请说明理由.
17.《哪吒2魔童闹海》票房大卖,周边玩偶热销.小洋在网上开设相关周边专卖店,一次,小洋发现一张进货单上的一个信息是:A款哪吒玩偶的进货单价比B款哪吒玩偶少5元,花500元购进A款哪吒玩偶的数量与花750元购进B款哪吒玩偶的数量相同.
(1)问: A、B两款的进货单价分别是多少元?
(2)小洋决定将A款玩偶的销售单价定为12元,将B款玩偶的销售单价定为20元,小洋打算要花费1000元购进A、B两款玩偶若干个,且A款的数量不小于B款的一半,请你根据计算说明,当A、B两款各购进多少时,小洋获得的总利润最高,最高为多少?
18.第19届亚运会已于2023年9月23日至10月8日在中国浙江杭州成功举行.这是党的二十大胜利召开之后我国举办的规模最大、水平最高的国际综合性体育赛事,举国关注,举世瞩目.杭州亚运会三个吉祥物分别取名“琮琮”“宸宸”“莲莲”.某专卖店购进,两种杭州亚运会吉祥物礼盒进行销售.种礼盒每个进价160元,售价220元;种礼盒每个进价120元,售价160元.现计划购进两种礼盒共100个,其中种礼盒不少于60个.设购进种礼盒个,两种礼盒全部售完,该专卖店获利元.
(1)求与之间的函数关系式;
(2)若购进100个礼盒的总费用不超过15000元,求该专卖店获得的最大利润为多少元?
19.、两地相距,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.
(1)求点C的坐标
(2)甲、乙两人离开A地的距离与时间的关系如图所示,则乙出发几小时后和甲相遇?
20.如图1,在同一平面直角坐标系中,直线与直线相交于点,与轴交于点,直线与轴交于点.
(1)填空: ___________, ___________, ___________;
(2)如图2,点为线段上一动点,将沿直线翻折得到,线段交轴于点.
①当点落在轴上时,求点的坐标;
②若为直角三角形,求点的坐标.
《第19章一次函数能力提升卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 D B D D D B
1.D
【分析】本题考查了一次函数图象与系数的关系,牢记“的图象在一、二、四象限”是解题的关键.
根据一次函数图象和性质进行判断即可.
【详解】解:∵一次函数的图象经过第一、二、四象限,
∴.
故选:D.
2.B
【分析】本题考查的是一次函数图象上点的坐标特点,分别把点,代入直线,求出,的值,再比较大小即可.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
【详解】解:点,都在直线上,
,.
,
.
故选:B.
3.D
【分析】本题考查了一次函数的应用,代入,,求得抵达目的地时的摄氏温度范围是解题的关键.
【详解】解:当时,,解得:,
当时,,解得:,
即:抵达目的地时的摄氏温度范围是.
这个温度范围比较低,属于冬季的温度范围,所以小王应建议妈妈抵达目的地时穿冬季服装,
故选:D.
4.D
【分析】本题考查了一次函数的应用,熟练掌握待定系数法是解题关键.根据点和,利用待定系数法求解即可得.
【详解】解:设与之间的函数关系式为,
将点和代入得:,
解得,
则与之间的函数关系式为,
故选:D.
5.D
【分析】本题考查了一次函数与坐标轴的交点,几何图形面积的计算,掌握一次函数图象的性质是解题的关键.
根据一次函数图象与坐标轴的交点,几何图形面积的计算公式计算即可.
【详解】解:一次函数,当时,,当时,,
∴,
故选:D .
6.B
【分析】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线在x轴上(或下)方部分所有的点的横坐标所构成的集合.观察函数图象得到当时,函数的图象都在的图象下方,所以不等式的解集为.
【详解】解:当时,函数的图象都在的图象下方,
所以不等式的解集为.
故选:B.
7.
【分析】此题考查了正比例的性质,把点的坐标代入即可求出答案.
【详解】解:∵点在正比例函数上,
∴
解得,
故答案为:
8.
【分析】本题考查的是一次函数图象的平移,利用待定系数法求解一次函数的解析式,掌握一次函数的平移规律是解题的关键.由直线向上平移个单位,其图象经过点,把代入平移后的解析式:即可得到答案.
【详解】解:设直线向上平移个单位,其图象经过点,
点在的图象上,
,
,
故答案为:
9.
【分析】本题考查了一次函数与一元一次不等式,根据函数图象即可得解,采用数形结合的思想是解此题的关键.
【详解】解:由图象可得,关于的不等式的解集是,
故答案为:.
10.
【分析】本题考查了两直线交点求二元一次方程组的解,理解两直线交点的含义是解题的关键.
根据两直线交点得到对应二元一次方程组的解即可.
【详解】解:∵函数与的图象交于点,
∴关于的方程组的解为,
故答案为: .
11.8
【分析】观察函数图象找出点的坐标,利用待定系数法求出线段和设的函数关系式,比较y值大小即可.
【详解】解:设y关于x的函数关系式为,
当时,将代入中得:
,
解得:,
∴;
当时,将代入中得:
,
解得:,
∴;
当时,,
当时,,
(元).
故答案为:8.
【点睛】本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,观察函数图象找出点的坐标,利用待定系数法求出线段和射线的函数关系式是解题的关键.
12.①③④
【分析】本题考查一次函数的定义、一次函数的图象与性质.根据一次函数的相关性质逐项分析求解即可.
【详解】解:若点,在该函数图象上,且,
,
y随x的增大而增大,则,说法正确,故①符合题意;
若该函数不经过第四象限,则,
,原说法错误,故②不符合题意;
正比例函数先向左平移一个单位,再向下平移2个单位得到,即,说法正确,故③符合题意;
令,则该函数恒过定点,说法正确,故④符合题意;
故符合题意的有①③④,
故答案为:①③④.
13.
【分析】本题考查了一次函数图象与系数的关系,一次函数图象上点的坐标特征,坐标与图形变化—对称,数形结合是解题的关键.
求得直线经过点关于直线的对称点时的的值,求得直线经过点关于直线的对称点时的的值,结合图形即可求解.
【详解】解:∵点,是过点与x轴垂直的直线,
∴关于直线的对称点为关于直线的对称点为,
如图,当经过点时,则,
解得,
当直线经过点时,则,解得,
故由图形可知,若直线上存在点,使点关于直线的对称点在的内部或边上,
则的取值范围是.
故答案为:.
14.
【分析】本题考查了根据函数图象获取信息,理解点的运动,函数图象中点的含义是解题的关键.
根据点的运动,函数图形的信息可得,当点运动到点时,,即,则,当点从点运动到点时,的面积是,可得,根据长方形的周长计算公式即可求解.
【详解】解:点是中点,点从点开始,沿着的路线匀速运动,
当点运动到点时,,即,
∴,
∴,
当点从点运动到点时,的面积是,
∴,
解得,,
∴长方形的周长为,
故答案为: .
15.(1)
(2)点在函数的图象上
【分析】本题考查了待定系数法求正比例函数解析式,也考查了正比例函数的性质.
(1)根据成正比例的定义,设,然后把已知的一组对应值代入求出k,从而得到y与x的函数关系式;
(2)利用(1)中的解析式,计算自变量为2对应的函数值,若函数值等于,则可判断点在这个函数的图象上.
【详解】(1)解:设,
把,代入得,
解得,
∴;
(2)解:∵时,,
∴点在函数的图象上.
16.(1)
(2)存在,点P的坐标为或
【分析】此题主要考查了一次函数的图象和性质,三角形的面积,熟练掌握待定系数法求一次函数的解析式,三角形的面积公式是解决问题的关键.
过点C作于点E,于点D,将点代入得,则直线的表达式为,进而可求出点,点,则,,再根据点得,,据此可得的面积;
先求出,设点P的坐标为,则,进而得,进而得,由此解出或,则点P的坐标为或
【详解】(1)解:过点C作于点E,于点D,如图所示:
线与直线有交点,
,
解得:,
直线的表达式为:,
对于,当时,,
当时,,解得:,
点,点,
,,
点,
,
;
(2)存在.
,,
,
点P在y轴上,
设点P的坐标为,
,
,
当的面积与的面积相等时,
,
,
或,
点P的坐标为或,
即当点的坐标为或时,的面积与的面积相等.
17.(1)A款的进货单价是10元,则B款的进货单价是15元
(2)购进A款25个,购进B款50个时,获得的总利润最高,最高为300元
【分析】本题考查分式方程的应用、一元一次不等式的应用、一次函数的应用,理解题意是解答的关键.
(1)设A款的进货单价是元,则B款的进货单价是元,根据题意列分式方程求解即可;
(2)设购进B款个,先根据“A款的数量不小于B款的一半”求得;再设总利润为,则,然后利用一次函数的性质求解即可.
【详解】(1)解:设A款的进货单价是元,则B款的进货单价是元,
根据题意,可得,
解得,
经检验,是该方程的解,
∴,
答:A款的进货单价是10元,则B款的进货单价是15元;
(2)解:设购进B款个,则购进A款个,
又A款的数量不小于B款的一半,
,
解得:,
设总利润为,则,
,
∴随的增大而增大,
当取得最大整数解50时,取得最大值,最大值为,
此时,则,
答:购进A款25个,购进B款50个时,获得的总利润最高,最高为300元.
18.(1)
(2)5500元
【分析】本题考查了一次函数的应用,一元一次不等式组的应用.
(1)根据利润等于单件利润乘以数量建立函数关系式即可;
(2)先求出自变量的取值范围,再根据一次函数增减性求最值.
【详解】(1)解:由题知,
与的函数表达式为.
(2)解:由题知
由(1)知
,
随的增大而增大,
当时,有最大值,(元).
19.(1)
(2)
【分析】(1)由题意得,点C的横坐标为,点C的纵坐标为,由此即可得出点C的坐标;
(2)设甲离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得;由“乙以的速度匀速行驶1小时后提高速度并继续匀速行驶”可知,乙的速度在和内是不同的,需要分别求解:设内乙离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得内函数解析式为,设内乙离开A地的距离与时间之间的函数解析式为,将,代入,得,解得,于是可得内函数解析式为,综上所述,;依题意,联立方程组,得,解方程组即可求出的值,进而可求出乙出发几小时后和甲相遇.
【详解】(1)解:由题意得:
点C的横坐标为:,
点C的纵坐标为:,
点C的坐标为;
(2)解:设甲离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
,
乙以的速度匀速行驶1小时后提高速度并继续匀速行驶,
乙的速度在和内是不同的,需要分别求解,
设内乙离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
内函数解析式为,
设内乙离开A地的距离与时间之间的函数解析式为,
将,代入,得:
,
解得:,
内函数解析式为,
综上所述,,
依题意,联立方程组,得:
,
解得:,
,
答:乙出发小时后和甲相遇.
【点睛】本题主要考查了一次函数的实际应用(行程问题),求一次函数解析式,两直线的交点与二元一次方程组的解,写出直角坐标系中点的坐标,从函数的图象获取信息,解二元一次方程组等知识点,能够从函数图象中获取正确信息并熟练掌握待定系数法求一次函数解析式是解题的关键.
20.(1),,
(2)①;②或
【分析】(1)把代入,求出,得直线,再把代入,求出,得点的坐标,最后把代入,求出;
(2)①过点作轴于点,作轴于点,求出,再求出,可得,即可得答案;②分两种情况讨论,当时,求出,得,得,得点坐标;当时,设,则,由勾股定理得:,求出,得点坐标.
【详解】(1)解:把代入得:,
解得:,
直线,
把代入得:
解得:,
,
把代入得:,
解得:.
故答案为:,,;
(2)①由(1)知直线,
令,则,
解得:
点,
如图,过点作轴于点,作轴于点,则,,
,
,
,
点的坐标为;
②如下图,
当时,由翻折得:,
,
,
,
,
点的坐标为;
如下图,
当时,,
设,则,
在中,由勾股定理得:,即,
解得:,
,
点的坐标为,
综上,点的坐标为或.
【点睛】此题考查了一次函数,勾股定理,等腰直角三角形的判定与性质,翻折的性质,解题的关键是作辅助线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
