人教A版(2019)必修第一册2.2 基本不等式 课件(共14张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册2.2 基本不等式 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 793.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
基本不等式
第24届国际数学家大会在北京召开
这是数学界的奥林匹克盛会.
本次大会
所使用的会标
据《周髀算经》记载,
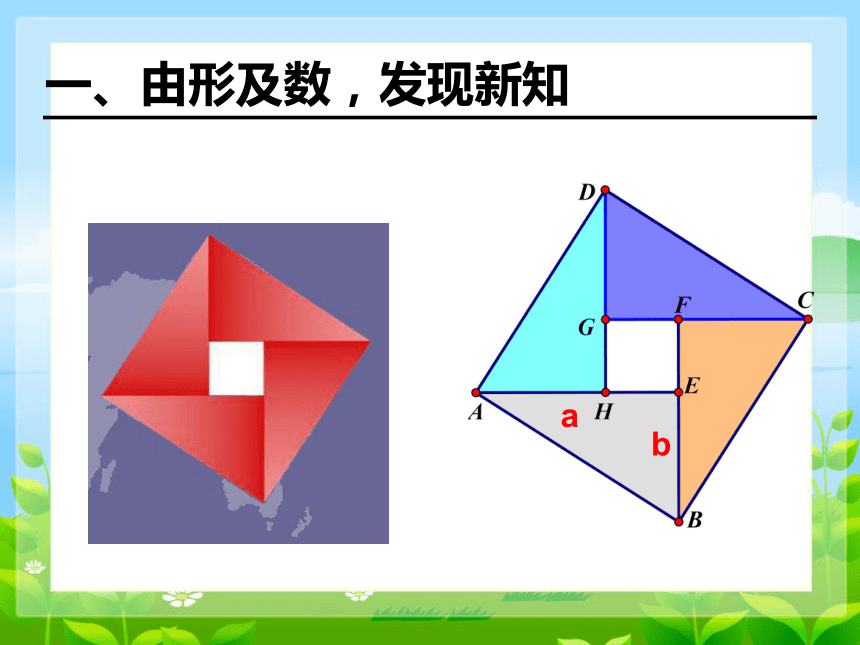
这是三国时期吴国的赵爽设计的勾股圆方图,
又称赵爽“弦图”,
通过此图最早证明了勾股定理。
a
b
一、由形及数,发现新知
你还能给出其它的证明方法吗?
二、理性分析,构建新知
证明:要证
只要证
要证①,只要证
要证②,只要证
显然, ③是成立的
当且仅当a=b时,③中的等号成立
分析法
你能从几何角度
对不等式进一步证明吗?
三、以形助数,理解新知
基本不等式的意义
发散提升
在直角三角形中
斜边中线大于斜边的高
在圆中
半径大于等于弦长的一半
两个正数的
等差中项大于等于等比中项
算数平均数大于几何平均数
例:判断下列问题的真假
四、简单应用,加深理解
(1)若 则 ,
当且仅当 ,即 时取等号. ( )
(2)若 则 ,
当且仅当 ,即 时取等号. ( )
例:判断下列问题的真假
四、简单应用,加深理解
(3)若 则 ,
当且仅当 ,即 时取等号. ( )
(4)若 ,则 ,
当且仅当 ,即 时取等号. ( )
能力提升
直观的
抽象的
相互联系的
图形
数
物理
半径不小于弦长的一半
算数平均数不小于
几何平均数
?
发散的
数学的思考问题
总结分享
谢谢
基本不等式
第24届国际数学家大会在北京召开
这是数学界的奥林匹克盛会.
本次大会
所使用的会标
据《周髀算经》记载,
这是三国时期吴国的赵爽设计的勾股圆方图,
又称赵爽“弦图”,
通过此图最早证明了勾股定理。
a
b
一、由形及数,发现新知
你还能给出其它的证明方法吗?
二、理性分析,构建新知
证明:要证
只要证
要证①,只要证
要证②,只要证
显然, ③是成立的
当且仅当a=b时,③中的等号成立
分析法
你能从几何角度
对不等式进一步证明吗?
三、以形助数,理解新知
基本不等式的意义
发散提升
在直角三角形中
斜边中线大于斜边的高
在圆中
半径大于等于弦长的一半
两个正数的
等差中项大于等于等比中项
算数平均数大于几何平均数
例:判断下列问题的真假
四、简单应用,加深理解
(1)若 则 ,
当且仅当 ,即 时取等号. ( )
(2)若 则 ,
当且仅当 ,即 时取等号. ( )
例:判断下列问题的真假
四、简单应用,加深理解
(3)若 则 ,
当且仅当 ,即 时取等号. ( )
(4)若 ,则 ,
当且仅当 ,即 时取等号. ( )
能力提升
直观的
抽象的
相互联系的
图形
数
物理
半径不小于弦长的一半
算数平均数不小于
几何平均数
?
发散的
数学的思考问题
总结分享
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
