勾股定理
图片预览




文档简介
课件17张PPT。14.1 勾股定理(2)---勾股定理的证明 两千多年来,人们对勾股定理的证明颇感兴趣。因为这个定理太贴近人们的生活实际,以致于古往今来,下至平民百姓,上至帝王总统都愿意探讨它的证明,因此不断涌现新的证法。下面我们一起学习几种证明勾股定理的方法。勾股定理:
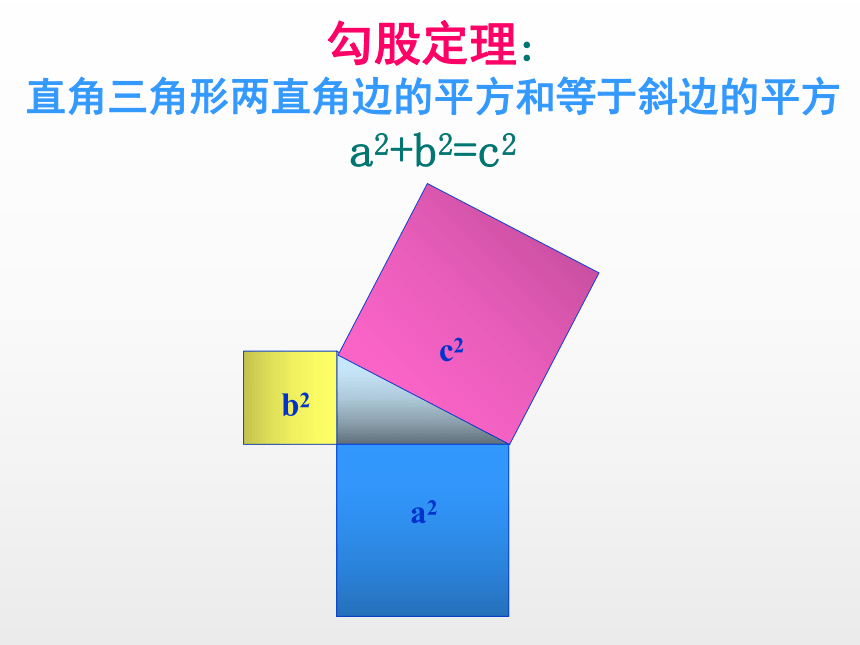
直角三角形两直角边的平方和等于斜边的平方
a2+b2=c2
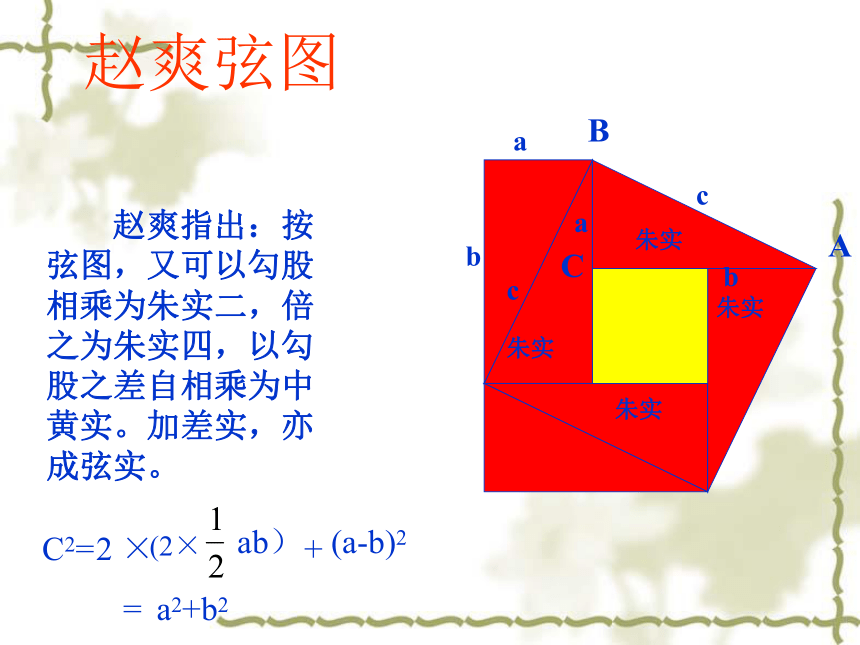
赵爽的“弦图” 早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”。
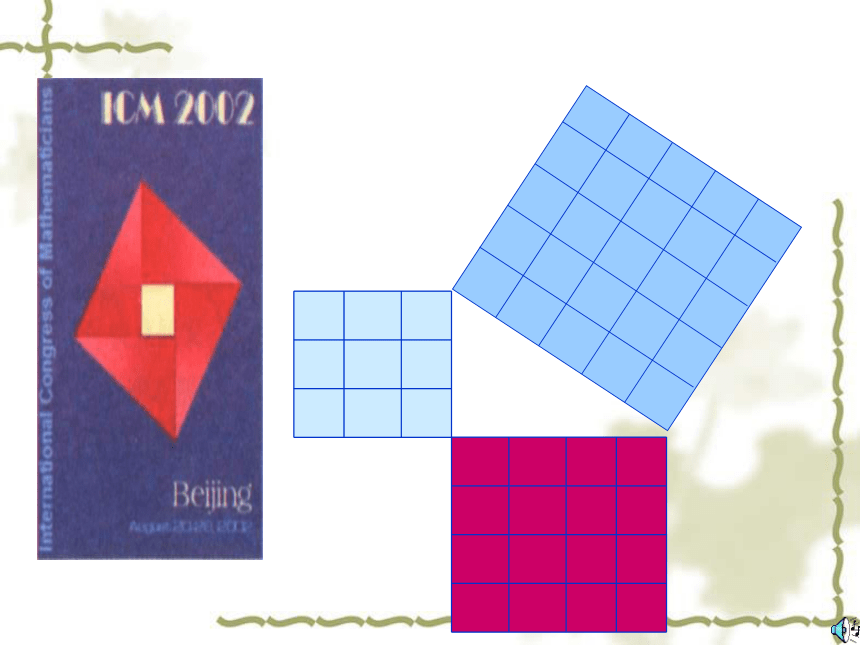
在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
思考:你能验证吗? 赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实。加差实,亦成弦实。赵爽弦图朱实朱实朱实C朱实C2=(2×ab)+(a-b)2a2+b2=2 ×(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证法一(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证法二 在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么,只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。证 法 3 (a + b)(b + a) =
a2 +
? a2 + b2 = c2aabbcc 伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟∟∟c2+ 2( )+ ab + b2 = c2abab ? a2 + b2 = c2a2b2a2c2毕达哥拉斯证法证 法 4: 你还想知道勾股定理的其它证法吗? 请上网查询,你一定会有精彩的发现。若你再能写一点有关勾股定理的小文章,那就更漂亮了。1、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活2、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离40应用知识回归生活课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。1这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?作业:P54_----55
1、4、5
赵爽的“弦图” 早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”。
在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
思考:你能验证吗? 赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实。加差实,亦成弦实。赵爽弦图朱实朱实朱实C朱实C2=(2×ab)+(a-b)2a2+b2=2 ×(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证法一(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证法二 在1876年一个周末的傍晚,美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么,只见一个小男孩正俯着身子,用树枝在地上画一个直角三角形,于是伽菲尔德便问,你们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别是3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少呢?”伽菲尔德不假思索地回答到:“那斜边的平方,一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?……”伽菲尔德一时语塞,无法解释了,心理很不是滋味。于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。证 法 3 (a + b)(b + a) =
a2 +
? a2 + b2 = c2aabbcc 伽菲尔德经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
∟∟∟c2+ 2( )+ ab + b2 = c2abab ? a2 + b2 = c2a2b2a2c2毕达哥拉斯证法证 法 4: 你还想知道勾股定理的其它证法吗? 请上网查询,你一定会有精彩的发现。若你再能写一点有关勾股定理的小文章,那就更漂亮了。1、如图,受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?应用知识回归生活2、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离40应用知识回归生活课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。1这节课你学到了什么知识?小 结:3、你还有什么疑惑或没有弄懂的地方?2 运用“勾股定理”应注意什么问题?作业:P54_----55
1、4、5
