【专项培优】北师大版数学七年级下册(2024)第四章三角形(含答案)
文档属性
| 名称 | 【专项培优】北师大版数学七年级下册(2024)第四章三角形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项培优】北师大版数学七年级下册(2024)第四章三角形
一、单选题
1.(2021七下·本溪期末)画△ABC的边BC上的高,下列画法正确的是( )
A. B.
C. D.
2.(2023九下·番禺期末)若长度分别是2,3,a的三条线段能组成一个三角形,则a的取值不可能是( )
A.1 B.2 C.3 D.4
3.(2024七下·南海月考)下列各组长度的线段为边,能构成三角形的是( )
A.、、 B.、、
C.、、 D.、、
4.(2024七下·子洲期末)在中,若,,则( )
A. B. C. D.
5.一定能确定△ABC≌△DEF的条件是 ( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.∠A=∠E,AB=EF,∠B=∠D
C.∠A=∠D,AB=DE,∠B=∠E D.AB=DE, BC=EF,∠A=∠D
二、填空题
6.(2019七下·海州期中)如图, ∥m,∠1=120°,∠A=55°,则∠ACB的大小是 .
7.(2023八上·袁州月考)如图,已知,,,,四点在一条直线上,若,,则的长是 .
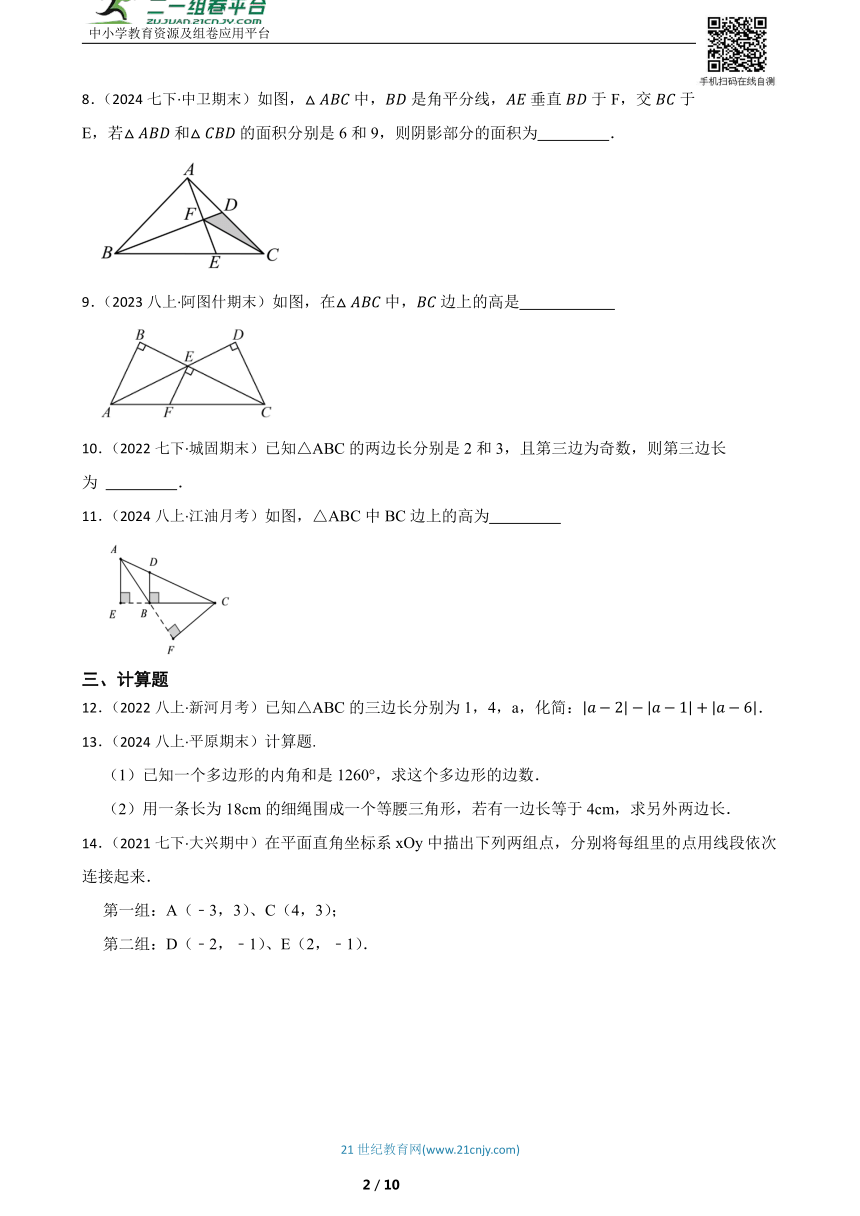
8.(2024七下·中卫期末)如图,中,是角平分线,垂直于F,交于E,若和的面积分别是6和9,则阴影部分的面积为 .
9.(2023八上·阿图什期末)如图,在中,边上的高是
10.(2022七下·城固期末)已知△ABC的两边长分别是2和3,且第三边为奇数,则第三边长为 .
11.(2024八上·江油月考)如图,△ABC中BC边上的高为
三、计算题
12.(2022八上·新河月考)已知△ABC的三边长分别为1,4,a,化简:.
13.(2024八上·平原期末)计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
14.(2021七下·大兴期中)在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
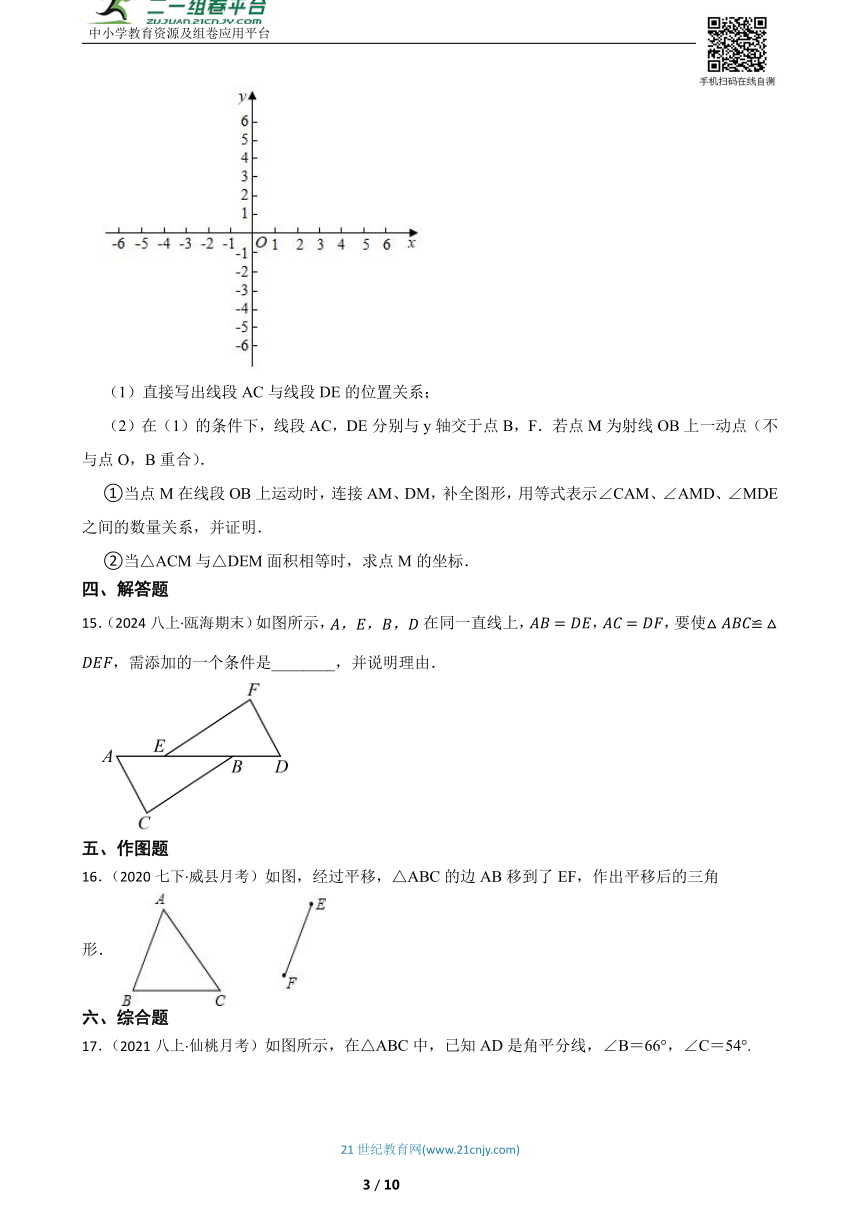
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
四、解答题
15.(2024八上·瓯海期末)如图所示,在同一直线上,,,要使,需添加的一个条件是________,并说明理由.
五、作图题
16.(2020七下·威县月考)如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.
六、综合题
17.(2021八上·仙桃月考)如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
18.(2020八上·颍州期末)如图,点 , , , 在一条直线上, , , .
求证:
(1) ;
(2) .
19.(2020八上·周口期中)某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
七、实践探究题
20.(2023八上·江城期中)[问题情境]
在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如题24图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D.
[探索发现]
(1)当∠A=60°时,求证:∠CBD=∠A.
(2)”快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系.
①当∠A=40°时,∠CBD= 度;
②当∠A=x°时,∠CBD= 度(用含x的代数式表示).
(3)[操作探究]
”智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变.请写出它们的关系,并说明理由.
答案解析部分
1.【答案】C
【知识点】三角形的角平分线、中线和高
2.【答案】A
【知识点】三角形三边关系
3.【答案】D
【知识点】三角形三边关系
4.【答案】A
【知识点】三角形内角和定理
5.【答案】C
【知识点】三角形全等的判定
6.【答案】65°
【知识点】平行线的性质;三角形内角和定理
7.【答案】5
【知识点】三角形全等及其性质
8.【答案】
【知识点】三角形的角平分线、中线和高
9.【答案】线段
【知识点】三角形的角平分线、中线和高
10.【答案】3
【知识点】三角形三边关系
11.【答案】AE
【知识点】三角形的角平分线、中线和高
12.【答案】
【知识点】三角形三边关系;化简含绝对值有理数
13.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
14.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
15.【答案】解:∵在同一直线上,,,
∴可添加条件:,理由如下:
在和中,
,
∴(SAS),
故答案为:.
【知识点】三角形全等的判定
16.【答案】如图所示:
【知识点】尺规作图-作三角形
17.【答案】(1)解:∵在△ABC中,∠B=66°,∠C=54°,∴∠BAC=180°-∠B-∠C=60°.∵AD是∠BAC的平分线,
∴∠BAD= ∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°
(2)解:∵∠CAD= ∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°
【知识点】三角形内角和定理
18.【答案】(1)证明: ,
,
,
在 和 中,
,
,
;
(2)证明:由(1)得: ,
,
.
【知识点】三角形全等的判定-SSS
19.【答案】(1)5
(2)解:由作法知,BC=DC,∠ABC=∠EDC=90°,
在△ABC和△EDC中, ,
∴△ABC≌△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
【知识点】全等三角形的应用
20.【答案】(1)证明:∵AM∥BN,
∴∠A+∠ABN= 180°.
又∵∠A=60°,
∴∠ABN=180°-∠A=180°-60°=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN.
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=×120°= 60°.
∴∠CBD=∠A
(2)70;(90-)
(3)解:∠APB=2∠ADB.理由如下:
∵BD平分∠PBN,
∴∠PBN=2∠NBD.
∵AM∥BN,
∴∠PBN=∠APB,∠NBD=∠ADB.
∴∠APB= =2∠ADB.
【知识点】平行线的性质;三角形内角和定理;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 10
【专项培优】北师大版数学七年级下册(2024)第四章三角形
一、单选题
1.(2021七下·本溪期末)画△ABC的边BC上的高,下列画法正确的是( )
A. B.
C. D.
2.(2023九下·番禺期末)若长度分别是2,3,a的三条线段能组成一个三角形,则a的取值不可能是( )
A.1 B.2 C.3 D.4
3.(2024七下·南海月考)下列各组长度的线段为边,能构成三角形的是( )
A.、、 B.、、
C.、、 D.、、
4.(2024七下·子洲期末)在中,若,,则( )
A. B. C. D.
5.一定能确定△ABC≌△DEF的条件是 ( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.∠A=∠E,AB=EF,∠B=∠D
C.∠A=∠D,AB=DE,∠B=∠E D.AB=DE, BC=EF,∠A=∠D
二、填空题
6.(2019七下·海州期中)如图, ∥m,∠1=120°,∠A=55°,则∠ACB的大小是 .
7.(2023八上·袁州月考)如图,已知,,,,四点在一条直线上,若,,则的长是 .
8.(2024七下·中卫期末)如图,中,是角平分线,垂直于F,交于E,若和的面积分别是6和9,则阴影部分的面积为 .
9.(2023八上·阿图什期末)如图,在中,边上的高是
10.(2022七下·城固期末)已知△ABC的两边长分别是2和3,且第三边为奇数,则第三边长为 .
11.(2024八上·江油月考)如图,△ABC中BC边上的高为
三、计算题
12.(2022八上·新河月考)已知△ABC的三边长分别为1,4,a,化简:.
13.(2024八上·平原期末)计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
14.(2021七下·大兴期中)在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
四、解答题
15.(2024八上·瓯海期末)如图所示,在同一直线上,,,要使,需添加的一个条件是________,并说明理由.
五、作图题
16.(2020七下·威县月考)如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.
六、综合题
17.(2021八上·仙桃月考)如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
18.(2020八上·颍州期末)如图,点 , , , 在一条直线上, , , .
求证:
(1) ;
(2) .
19.(2020八上·周口期中)某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
七、实践探究题
20.(2023八上·江城期中)[问题情境]
在综合实践课上,老师组织班上的同学开展了探究两角之间数量关系的数学活动,如题24图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,且分别交射线AM于点C,D.
[探索发现]
(1)当∠A=60°时,求证:∠CBD=∠A.
(2)”快乐小组”经过探索后发现:不断改变∠A的度数,∠CBD与∠A始终存在某种数量关系.
①当∠A=40°时,∠CBD= 度;
②当∠A=x°时,∠CBD= 度(用含x的代数式表示).
(3)[操作探究]
”智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变.请写出它们的关系,并说明理由.
答案解析部分
1.【答案】C
【知识点】三角形的角平分线、中线和高
2.【答案】A
【知识点】三角形三边关系
3.【答案】D
【知识点】三角形三边关系
4.【答案】A
【知识点】三角形内角和定理
5.【答案】C
【知识点】三角形全等的判定
6.【答案】65°
【知识点】平行线的性质;三角形内角和定理
7.【答案】5
【知识点】三角形全等及其性质
8.【答案】
【知识点】三角形的角平分线、中线和高
9.【答案】线段
【知识点】三角形的角平分线、中线和高
10.【答案】3
【知识点】三角形三边关系
11.【答案】AE
【知识点】三角形的角平分线、中线和高
12.【答案】
【知识点】三角形三边关系;化简含绝对值有理数
13.【答案】(1)9;(2)7 cm ,7 cm.
【知识点】三角形三边关系
14.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
15.【答案】解:∵在同一直线上,,,
∴可添加条件:,理由如下:
在和中,
,
∴(SAS),
故答案为:.
【知识点】三角形全等的判定
16.【答案】如图所示:
【知识点】尺规作图-作三角形
17.【答案】(1)解:∵在△ABC中,∠B=66°,∠C=54°,∴∠BAC=180°-∠B-∠C=60°.∵AD是∠BAC的平分线,
∴∠BAD= ∠BAC=30°.
在△ABD中,∠B=66°,∠BAD=30°,
∴∠ADB=180°-∠B-∠BAD=84°
(2)解:∵∠CAD= ∠BAC=30°,DE⊥AC,
∴∠ADE=90°-∠EAD=60°
【知识点】三角形内角和定理
18.【答案】(1)证明: ,
,
,
在 和 中,
,
,
;
(2)证明:由(1)得: ,
,
.
【知识点】三角形全等的判定-SSS
19.【答案】(1)5
(2)解:由作法知,BC=DC,∠ABC=∠EDC=90°,
在△ABC和△EDC中, ,
∴△ABC≌△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
【知识点】全等三角形的应用
20.【答案】(1)证明:∵AM∥BN,
∴∠A+∠ABN= 180°.
又∵∠A=60°,
∴∠ABN=180°-∠A=180°-60°=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN.
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=×120°= 60°.
∴∠CBD=∠A
(2)70;(90-)
(3)解:∠APB=2∠ADB.理由如下:
∵BD平分∠PBN,
∴∠PBN=2∠NBD.
∵AM∥BN,
∴∠PBN=∠APB,∠NBD=∠ADB.
∴∠APB= =2∠ADB.
【知识点】平行线的性质;三角形内角和定理;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 10
同课章节目录
