第九章图形的变换章节期中复习(含解析)
文档属性
| 名称 | 第九章图形的变换章节期中复习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 820.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 21:11:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章图形的变换章节期中复习苏科版2024—2025学年七年级下册
一、选择题
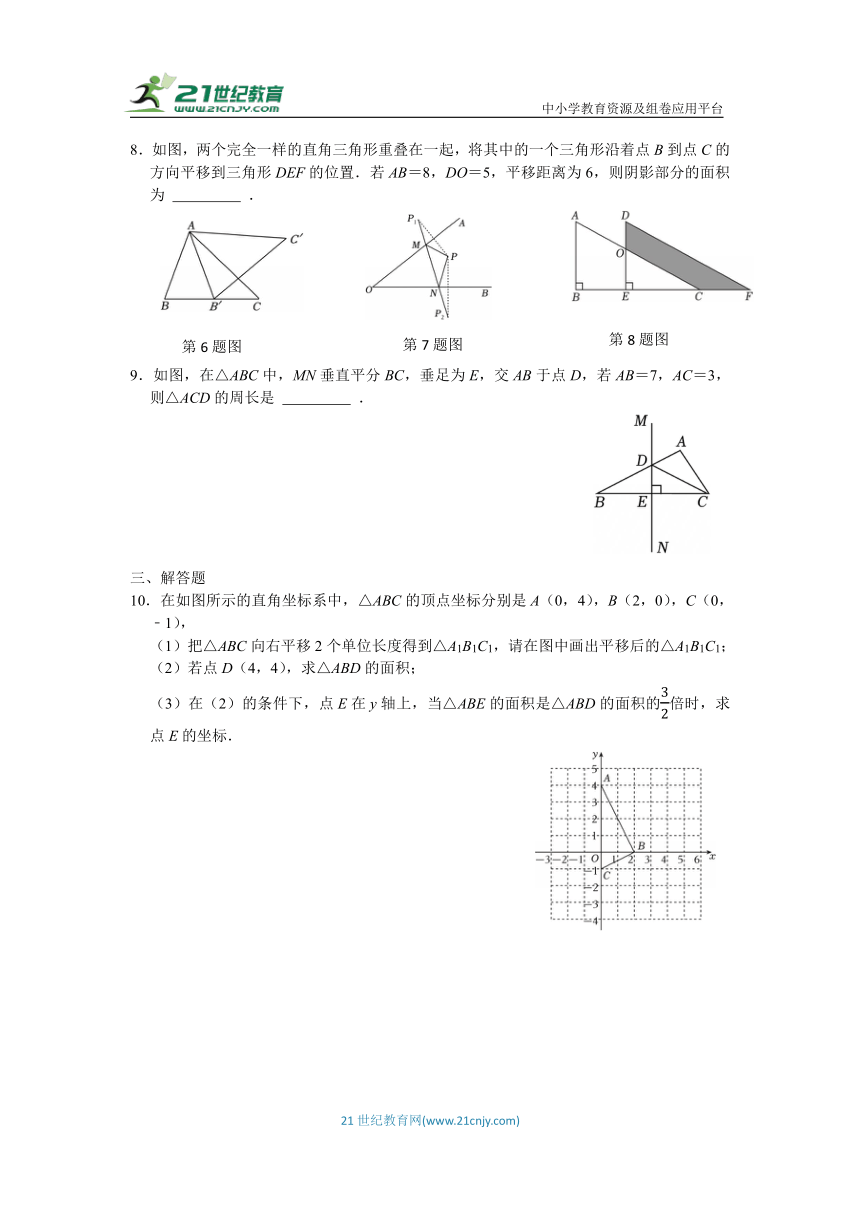
1.如图,将△ABC向右平移得到△DEF,且点B,E,C,F在同一条直线上,若EC=2,BF=8,则AD的长为( )
A.2 B.3 C.5 D.6
2.围棋起源于中国,距今已有4000多年的历史,小萍与人工智能机器人进行了围棋人机对战.截取对战棋谱中的四个部分,由黑白棋子摆成的图案是轴对称图形的是( )
A. B. C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图,MP、NQ,分别是AB,AC的垂直平分线,若△AMN的周长为10,则BC的长为( )
A.8 B.10 C.12 D.20
5.如图,△ABC绕点A逆时针旋转20°得到△AB′C′,点C恰好落在B′C′上,则∠ACB的度数为( )
A.60° B.70° C.80° D.90°
二、填空题
6.如图,将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,已知∠BAC=70°,则∠C′= .
7.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是3cm,则P1P2的长为 .
8.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到三角形DEF的位置.若AB=8,DO=5,平移距离为6,则阴影部分的面积为 .
9.如图,在△ABC中,MN垂直平分BC,垂足为E,交AB于点D,若AB=7,AC=3,则△ACD的周长是 .
三、解答题
10.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,4),B(2,0),C(0,﹣1),
(1)把△ABC向右平移2个单位长度得到△A1B1C1,请在图中画出平移后的△A1B1C1;
(2)若点D(4,4),求△ABD的面积;
(3)在(2)的条件下,点E在y轴上,当△ABE的面积是△ABD的面积的倍时,求点E的坐标.
11.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
12.如图,方格纸上每个小方格的边长都是1,△ABC与△A1B1C1成中心对称.
(1)画出对称中心O;
(2)画出将△A1B1C1向上平移6个单位长度得到的△A2B2C2;
(3)△A2B2C2绕点C2按顺时针方向至少旋转多少度,才能与△CC1C2重合?
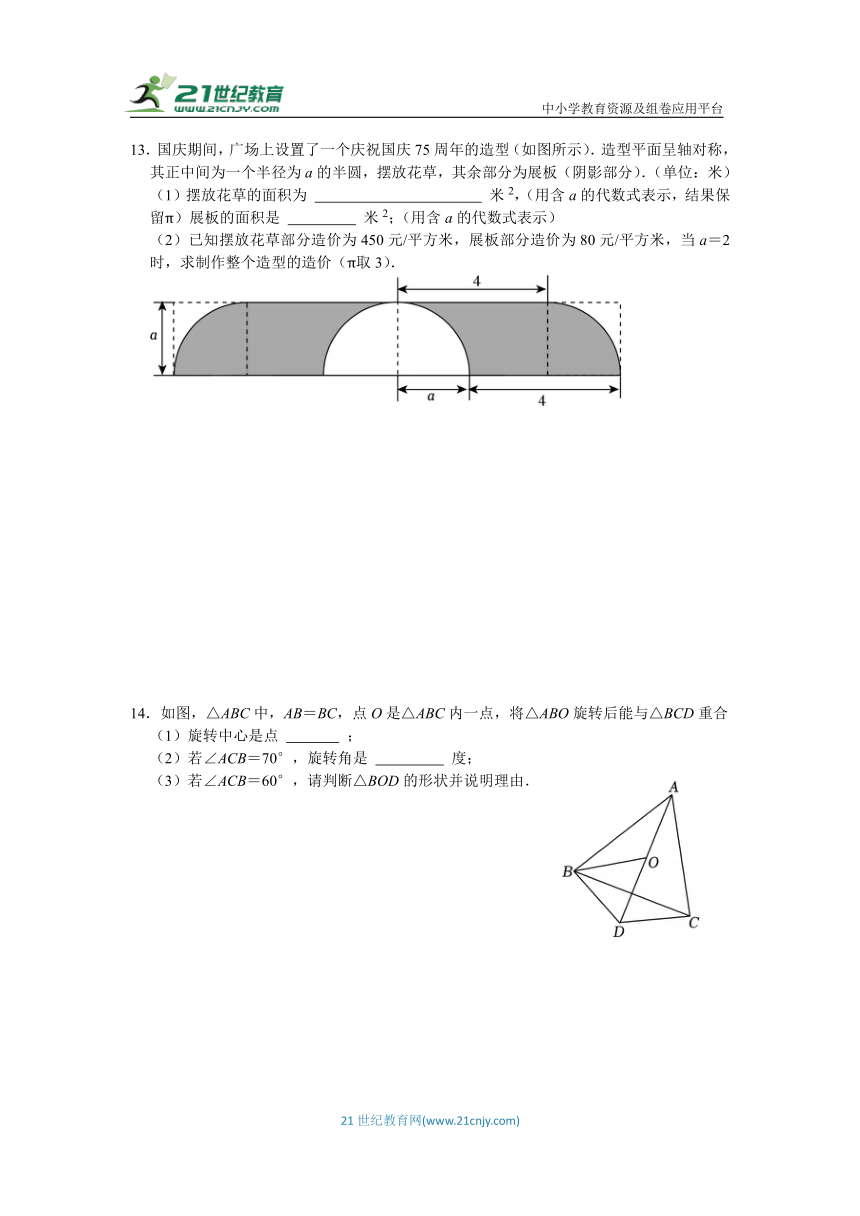
13.国庆期间,广场上设置了一个庆祝国庆75周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为a的半圆,摆放花草,其余部分为展板(阴影部分).(单位:米)
(1)摆放花草的面积为 米2,(用含a的代数式表示,结果保留π)展板的面积是 米2;(用含a的代数式表示)
(2)已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,当a=2时,求制作整个造型的造价(π取3).
14.如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合
(1)旋转中心是点 ;
(2)若∠ACB=70°,旋转角是 度;
(3)若∠ACB=60°,请判断△BOD的形状并说明理由.
15.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
16.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC,BC于点M、N.
(1)如图1,若∠BAC=112°,求∠EAN的度数;
(2)如图2,若∠BAC=82°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
参考答案
一、选择题
1.【解答】解:∵△DEF是由△ABC向右平移得到,
∴BC=EF,AD=BE,
∴BE=CF=(8﹣2)÷2=3,
∴AD=BE=3.
故选:B.
2.【解答】解:A、C、D中的图形不是轴对称图形,故A、C、D不符合题意;
B图形是轴对称图形,故B符合题意.
故选:B.
3.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
4.【解答】解:∵MP,NQ分别是AB,AC的垂直平分线,
∴AM=BM,AN=CN,
∵△AMN的周长为10,
∴AM+MN+AN=10,
∴BM+MN+CN=10,
即BC=10.
故选:B.
5.【解答】解:∵△ABC绕点A逆时针旋转20°得到△AB′C′,
∴∠CAC'=20°,AC=AC',∠ACB=∠C',
∴∠ACB=∠C'80°,
故选:C.
二、填空题
6.【解答】解:∵将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,
∴∠BAB'=30°,AB=AB',∠C=∠C',
∴∠ABB'=∠AB'B=(180°﹣30°)÷2=75°,
∵∠BAC=70°,
∴∠B'AC=∠BAC﹣∠BAB'=70°﹣30°=40°,
∴∠C=∠AB'B﹣∠B'AC=75°﹣40°=35°,
∴∠C'=35°.
故答案为:35°.
7.【解答】解:∵P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N,
∴MP=MP1,NP=NP2,
∵△PMN的周长是3cm,
∴MP+MN+NP=3cm,
∴P1P2=MP1+MN+NP2=MP+MN+NP=3cm.
故答案为:3cm.
8.【解答】解:由平移的性质知,BE=6,DE=AB=8,
∴OE=DE﹣DO=8﹣5=3,
由平移可知,S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO(AB+OE) BE(8+3)×6=33.
故答案为:33.
9.【解答】解:∵MN垂直平分BC,
∴DB=DC,
∵AB=7,AC=3,
∴△ACD的周长=AC+AD+DC=AC+AD+DB=AC+AB=3+7=10,
故答案为:10.
三、解答题
10.【解答】解:(1)如图1,△A1B1C1即为所求;
(2)如图2,
由网格可知AD=4,
∴△ABD的面积为;
(3)∵点E在y轴上,
∴设E(0,y),则AE=|y﹣4|,
由(2)得:△ABD的面积为8,
∵△ABE的面积是△ABD的面积的倍,
∴△ABE的面积是,
∴,
解得y=16或﹣8,
∴点E的坐标为(0,16)或(0,﹣8).
11.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
12.【解答】解:(1)连接AA1,BB1,CC1,交于点O,
则点O即为所求.
(2)如图,△A2B2C2即为所求.
(3)连接CC2,C1C2,
由图可知,△A2B2C2绕点C2按顺时针方向至少旋转90°,才能与△CC1C2重合.
13.【解答】解:(1)摆放花草的面积为米2,展板的面积是8a米2;
故答案为:,8a;
(2)造价为:3980(元).
答:制作整个造型的造价为3980元.
14.【解答】解:(1)旋转中心是点B,
故答案为:B;
(2)∵AB=BC,
∴∠BAC=∠ACB=70°,
∴∠ABC=180°﹣∠BAC﹣∠ACB=40°,
∵将△ABO旋转后能与△BCD重合,
∴∠ABO=∠CBD,
∴∠OBC+∠ABO=∠OBC+∠CBD=∠ABC=40°,
∵旋转角是40度,
故答案为:40;
(3)△BOD是等边三角形,
∵AB=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵将△ABO旋转后能与△BCD重合,
∴BD=BO,
∵∠OBD=∠ABC=60°,
∴△BOD是等边三角形.
15.【解答】解:(1)∵l1是线段AB的垂直平分线,
∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,
∴EA=EC,
∵△ADE的周长为6,
∴AD+DE+AE=6,
∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,
∴OA=OB,
∵l2是线段AC的垂直平分线,
OA=OC,
∴OB=OC,
∵△OBC的周长为16,BC=6,
∴OB+OC=10,
∴OA=OB=OC=5.
16.【解答】解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,
=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=68°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=112°﹣68°=44°;
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC,
=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=98°,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=98°﹣82°=16°;
(3)当0°<α<90°时,∠EAN=180°﹣2α;
当180°>α>90°时,∠EAN=2α﹣180°.
21世纪教育网(www.21cnjy.com)
第九章图形的变换章节期中复习苏科版2024—2025学年七年级下册
一、选择题
1.如图,将△ABC向右平移得到△DEF,且点B,E,C,F在同一条直线上,若EC=2,BF=8,则AD的长为( )
A.2 B.3 C.5 D.6
2.围棋起源于中国,距今已有4000多年的历史,小萍与人工智能机器人进行了围棋人机对战.截取对战棋谱中的四个部分,由黑白棋子摆成的图案是轴对称图形的是( )
A. B. C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图,MP、NQ,分别是AB,AC的垂直平分线,若△AMN的周长为10,则BC的长为( )
A.8 B.10 C.12 D.20
5.如图,△ABC绕点A逆时针旋转20°得到△AB′C′,点C恰好落在B′C′上,则∠ACB的度数为( )
A.60° B.70° C.80° D.90°
二、填空题
6.如图,将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,已知∠BAC=70°,则∠C′= .
7.如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是3cm,则P1P2的长为 .
8.如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点B到点C的方向平移到三角形DEF的位置.若AB=8,DO=5,平移距离为6,则阴影部分的面积为 .
9.如图,在△ABC中,MN垂直平分BC,垂足为E,交AB于点D,若AB=7,AC=3,则△ACD的周长是 .
三、解答题
10.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,4),B(2,0),C(0,﹣1),
(1)把△ABC向右平移2个单位长度得到△A1B1C1,请在图中画出平移后的△A1B1C1;
(2)若点D(4,4),求△ABD的面积;
(3)在(2)的条件下,点E在y轴上,当△ABE的面积是△ABD的面积的倍时,求点E的坐标.
11.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为20,求BC的长.
12.如图,方格纸上每个小方格的边长都是1,△ABC与△A1B1C1成中心对称.
(1)画出对称中心O;
(2)画出将△A1B1C1向上平移6个单位长度得到的△A2B2C2;
(3)△A2B2C2绕点C2按顺时针方向至少旋转多少度,才能与△CC1C2重合?
13.国庆期间,广场上设置了一个庆祝国庆75周年的造型(如图所示).造型平面呈轴对称,其正中间为一个半径为a的半圆,摆放花草,其余部分为展板(阴影部分).(单位:米)
(1)摆放花草的面积为 米2,(用含a的代数式表示,结果保留π)展板的面积是 米2;(用含a的代数式表示)
(2)已知摆放花草部分造价为450元/平方米,展板部分造价为80元/平方米,当a=2时,求制作整个造型的造价(π取3).
14.如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合
(1)旋转中心是点 ;
(2)若∠ACB=70°,旋转角是 度;
(3)若∠ACB=60°,请判断△BOD的形状并说明理由.
15.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
16.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC,BC于点M、N.
(1)如图1,若∠BAC=112°,求∠EAN的度数;
(2)如图2,若∠BAC=82°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出用α表示∠EAN大小的代数式.
参考答案
一、选择题
1.【解答】解:∵△DEF是由△ABC向右平移得到,
∴BC=EF,AD=BE,
∴BE=CF=(8﹣2)÷2=3,
∴AD=BE=3.
故选:B.
2.【解答】解:A、C、D中的图形不是轴对称图形,故A、C、D不符合题意;
B图形是轴对称图形,故B符合题意.
故选:B.
3.【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、既是轴对称图形,又是中心对称图形,符合题意;
故选:D.
4.【解答】解:∵MP,NQ分别是AB,AC的垂直平分线,
∴AM=BM,AN=CN,
∵△AMN的周长为10,
∴AM+MN+AN=10,
∴BM+MN+CN=10,
即BC=10.
故选:B.
5.【解答】解:∵△ABC绕点A逆时针旋转20°得到△AB′C′,
∴∠CAC'=20°,AC=AC',∠ACB=∠C',
∴∠ACB=∠C'80°,
故选:C.
二、填空题
6.【解答】解:∵将△ABC绕点A逆时针旋转30°得到△AB′C′,且B′恰好落在边BC上,
∴∠BAB'=30°,AB=AB',∠C=∠C',
∴∠ABB'=∠AB'B=(180°﹣30°)÷2=75°,
∵∠BAC=70°,
∴∠B'AC=∠BAC﹣∠BAB'=70°﹣30°=40°,
∴∠C=∠AB'B﹣∠B'AC=75°﹣40°=35°,
∴∠C'=35°.
故答案为:35°.
7.【解答】解:∵P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N,
∴MP=MP1,NP=NP2,
∵△PMN的周长是3cm,
∴MP+MN+NP=3cm,
∴P1P2=MP1+MN+NP2=MP+MN+NP=3cm.
故答案为:3cm.
8.【解答】解:由平移的性质知,BE=6,DE=AB=8,
∴OE=DE﹣DO=8﹣5=3,
由平移可知,S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO(AB+OE) BE(8+3)×6=33.
故答案为:33.
9.【解答】解:∵MN垂直平分BC,
∴DB=DC,
∵AB=7,AC=3,
∴△ACD的周长=AC+AD+DC=AC+AD+DB=AC+AB=3+7=10,
故答案为:10.
三、解答题
10.【解答】解:(1)如图1,△A1B1C1即为所求;
(2)如图2,
由网格可知AD=4,
∴△ABD的面积为;
(3)∵点E在y轴上,
∴设E(0,y),则AE=|y﹣4|,
由(2)得:△ABD的面积为8,
∵△ABE的面积是△ABD的面积的倍,
∴△ABE的面积是,
∴,
解得y=16或﹣8,
∴点E的坐标为(0,16)或(0,﹣8).
11.【解答】解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(2)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(1)可知,DA=DB,FA=FC,
∴BC=DB+DF+FC=DA+DF+FA=20.
12.【解答】解:(1)连接AA1,BB1,CC1,交于点O,
则点O即为所求.
(2)如图,△A2B2C2即为所求.
(3)连接CC2,C1C2,
由图可知,△A2B2C2绕点C2按顺时针方向至少旋转90°,才能与△CC1C2重合.
13.【解答】解:(1)摆放花草的面积为米2,展板的面积是8a米2;
故答案为:,8a;
(2)造价为:3980(元).
答:制作整个造型的造价为3980元.
14.【解答】解:(1)旋转中心是点B,
故答案为:B;
(2)∵AB=BC,
∴∠BAC=∠ACB=70°,
∴∠ABC=180°﹣∠BAC﹣∠ACB=40°,
∵将△ABO旋转后能与△BCD重合,
∴∠ABO=∠CBD,
∴∠OBC+∠ABO=∠OBC+∠CBD=∠ABC=40°,
∵旋转角是40度,
故答案为:40;
(3)△BOD是等边三角形,
∵AB=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵将△ABO旋转后能与△BCD重合,
∴BD=BO,
∵∠OBD=∠ABC=60°,
∴△BOD是等边三角形.
15.【解答】解:(1)∵l1是线段AB的垂直平分线,
∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,
∴EA=EC,
∵△ADE的周长为6,
∴AD+DE+AE=6,
∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,
∴OA=OB,
∵l2是线段AC的垂直平分线,
OA=OC,
∴OB=OC,
∵△OBC的周长为16,BC=6,
∴OB+OC=10,
∴OA=OB=OC=5.
16.【解答】解:(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,
=∠BAC﹣(∠B+∠C),
在△ABC中,∠B+∠C=180°﹣∠BAC=68°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=112°﹣68°=44°;
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN﹣∠BAC,
=(∠B+∠C)﹣∠BAC,
在△ABC中,∠B+∠C=180°﹣∠BAC=98°,
∴∠EAN=∠BAE+∠CAN﹣∠BAC=98°﹣82°=16°;
(3)当0°<α<90°时,∠EAN=180°﹣2α;
当180°>α>90°时,∠EAN=2α﹣180°.
21世纪教育网(www.21cnjy.com)
同课章节目录
