第八章整式乘法章节期中复习(含解析)
文档属性
| 名称 | 第八章整式乘法章节期中复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 315.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章整式乘法章节期中复习苏科版2024—2025学年七年级下册
一、选择题
1.计算(a﹣b)(a+b)(a2+b2)(a4+b4)等于( )
A.a4﹣b4 B.a6+b6 C.a6﹣b6 D.a8﹣b8
2.若(x+2)(x﹣3)=x2+ax﹣6,则a的值为( )
A.﹣1 B.1 C.3 D.5
3.若a+b=0,ab=﹣11,则a2+b2的值是( )
A.﹣11 B.11 C.﹣22 D.22
4.下列运算正确的是( )
A.(﹣x﹣y)2=x2+2xy+y2 B.(﹣a﹣b) (a+b)=a2﹣b2
C.(m﹣3)(m+2)=m2﹣6 D.(a﹣b)2=a2﹣b2
5.下列整式乘法能用平方差公式计算的是( )
A.(2a+b)(a﹣2b) B.(b+2a)(2a﹣b)
C.(b﹣2a)(2a﹣b) D.(a﹣2b)(2b﹣a)
6.在下面的正方形分割方案中,可以验证(a+b)2=(a﹣b)2+4ab的图形是( )
A. B.
C. D.
7.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到a2+3ab+2b2=(a+2b)(a+b).若已知a2+b2+c2=69,ab+bc+ac=50,由图2所表示的数学等式,则a+b+c的值为( )
A.1 B.12 C.13 D.14
8.如图,在矩形ABCD中,AB=10,BC=5,点M和点N分别在AB和BC边上,并且AM﹣CN=1,分别以BM和BN为边向上、向右作正方形,两个正方形的面积分别为S1和S2,且S1+S2=50,则图中阴影部分的面积为( )
A.15 B.17
C.19 D.21
二、填空题
9.已知(m﹣n)2=32,(m+n)2=200,则m2+n2的值为 .
10.在长为(3a+2)、宽为(2a+3)的长方形铁皮上剪去一个边长为(a﹣1)的小正方形,则剩余部分的面积为 .
11.若代数式m2﹣km+1是一个完全平方式,则实数k= .
12.要使(x2+ax﹣1)(﹣2x3+x2)的展开式中不含x4项,则a的值为 .
三、解答题
13.简便运算:
(1)20242﹣2023×2025;
(2)186.72﹣2×186.7×86.7+86.72.
14.如图,某学校有一块长为(5a+b)m,宽为(2a+b)m的长方形土地,计划在阴影部分的区域进行绿化,中间修建一个边长为(a+b)m的正方形喷水池.
(1)用含a,b的代数式表示绿化面积;
(2)当a=1,b=2时,求绿化面积.
15.计算:
(1)(﹣2ab)(3a2﹣2ab﹣4b2);
(2)(2x﹣1)(x﹣4)﹣(x+3)(x+2).
16.在计算(2x+a)(x+b)时,甲错把b看成了6,得到的结果是2x2+8x﹣24,乙错把a看成了﹣a,得到的结果是2x2+14x+20.
(1)求a、b的值;
(2)求(2x+a)(x+b)的正确结果.
17.关于x的代数式(ax﹣3)(2x+1)﹣4x2+m化简后不含有x2项和常数项.
(1)求a和m的值.
(2)若an+mn=﹣5,求代数式﹣4n2+3m的值.
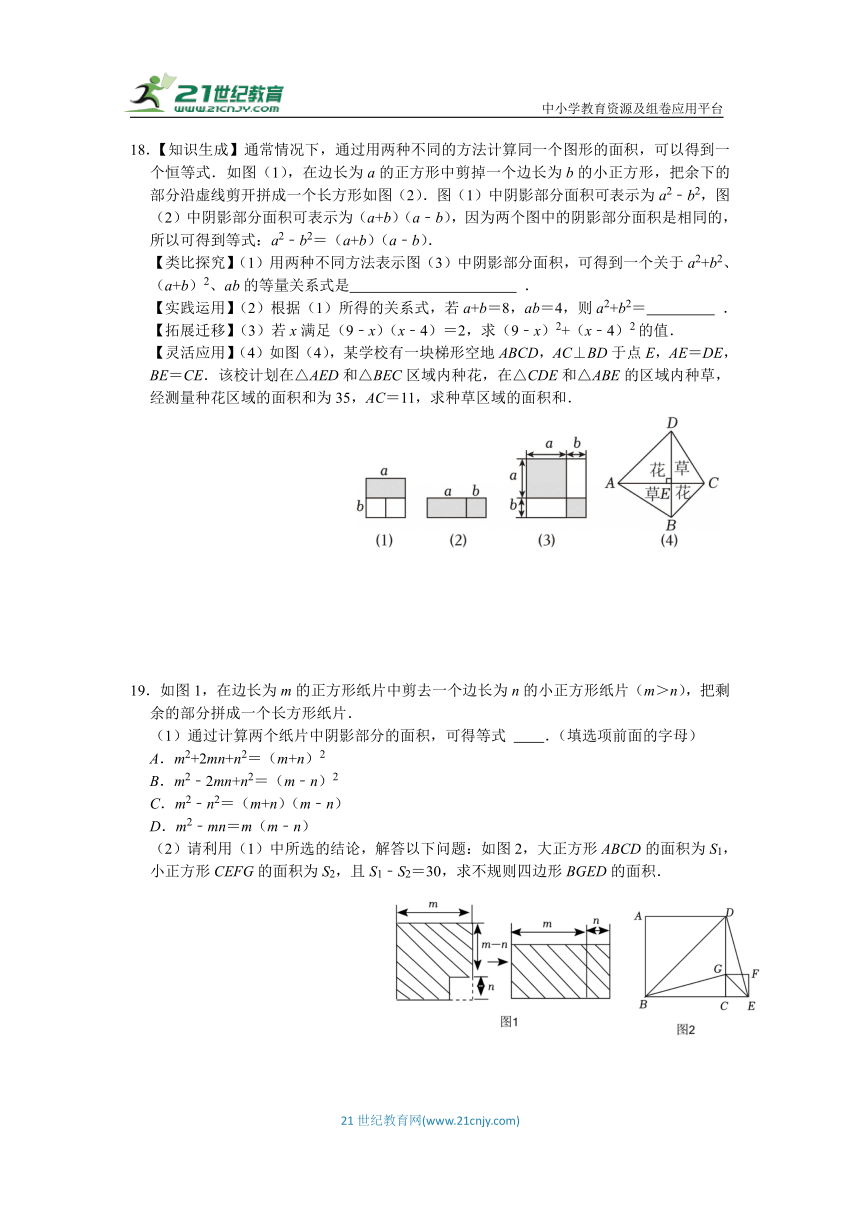
18.【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图(1),在边长为a的正方形中剪掉一个边长为b的小正方形,把余下的部分沿虚线剪开拼成一个长方形如图(2).图(1)中阴影部分面积可表示为a2﹣b2,图(2)中阴影部分面积可表示为(a+b)(a﹣b),因为两个图中的阴影部分面积是相同的,所以可得到等式:a2﹣b2=(a+b)(a﹣b).
【类比探究】(1)用两种不同方法表示图(3)中阴影部分面积,可得到一个关于a2+b2、(a+b)2、ab的等量关系式是 .
【实践运用】(2)根据(1)所得的关系式,若a+b=8,ab=4,则a2+b2= .
【拓展迁移】(3)若x满足(9﹣x)(x﹣4)=2,求(9﹣x)2+(x﹣4)2的值.
【灵活应用】(4)如图(4),某学校有一块梯形空地ABCD,AC⊥BD于点E,AE=DE,BE=CE.该校计划在△AED和△BEC区域内种花,在△CDE和△ABE的区域内种草,经测量种花区域的面积和为35,AC=11,求种草区域的面积和.
19.如图1,在边长为m的正方形纸片中剪去一个边长为n的小正方形纸片(m>n),把剩余的部分拼成一个长方形纸片.
(1)通过计算两个纸片中阴影部分的面积,可得等式 .(填选项前面的字母)
A.m2+2mn+n2=(m+n)2
B.m2﹣2mn+n2=(m﹣n)2
C.m2﹣n2=(m+n)(m﹣n)
D.m2﹣mn=m(m﹣n)
(2)请利用(1)中所选的结论,解答以下问题:如图2,大正方形ABCD的面积为S1,小正方形CEFG的面积为S2,且S1﹣S2=30,求不规则四边形BGED的面积.
参考答案
一、选择题
1.解:(a﹣b)(a+b)(a2+b2)(a4+b4)
=(a2﹣b2)(a2+b2)(a4+b4)
=(a4﹣b4)(a4+b4)
=a8﹣b8,
故选:D.
2.解:(x+2)(x﹣3)
=x2﹣3x+2x﹣6
=x2﹣x﹣6,
∵(x+2)(x﹣3)=x2+ax﹣6,
∴a=﹣1,
故选:A.
3.解:由条件可知(a+b)2=a2+b2+2ab=0,
∵ab=﹣11,
∴a2+b2+2×(﹣11)=0,
∴a2+b2=22,
故选:D.
4.解:A、(﹣x﹣y)2=x2+2xy+y2,正确;
B、(﹣a﹣b) (a+b)=﹣a2﹣b2﹣2ab,错误;
C、(m﹣3)(m+2)=m2﹣m﹣6,错误;
D、(a﹣b)2=a2+b2﹣2ab,错误,
故选:A.
5.解:(2a+b)(a﹣2b)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则A不符合题意,
(b+2a)(2a﹣b)是两式的和与相同两式的差的积,它能用平方差公式计算,则B符合题意,
(b﹣2a)(2a﹣b)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则C不符合题意,
(a﹣2b)(2b﹣a)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则D不符合题意,
故选:B.
6.解:∵由选项A可得a2﹣b2=(a+b)(a﹣b),
∴选项A不符合题意;
∵由选项B可得(a+b)2=a2+2ab+b2,
∴选项B不符合题意;
∵由选项C可得(a﹣b)2=a2﹣2ab+b2.
∴选项C不符合题意;
∵由选项D可得(a+b)2=(a﹣b)2+4ab,
∴选项D符合题意;
故选:D.
7.解:由图2可得(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
∴(a+b+c)2=a2+b2+c2+2(ab+bc+ac)=69+2×50=169,
又∵a+b+c>0,
∴a+b+c=13,
故选:C.
8.解:设AM=x,则CN=x﹣1,
∴BM=AB﹣AM=10﹣x,BN=5﹣(x﹣1)=6﹣x,
∵S1+S2=50,
∴(10﹣x)2+(6﹣x)2=50,
∴x=8或x=8(不合题意舍去),
∴,BN2,
∴图中阴影部分的面积为BM BN17,
故选:B.
二、填空题
9.解:(m﹣n)2=m2﹣2mn+n2=32①,
(m+n)2=m2+2mn+n2=200②,
②+①得,2m2+2n2=232,
解得:m2+n2=116.
故答案为:116.
10.解:根据题意得:(3a+2)(2a+3)﹣(a﹣1)2=6a2+9a+4a+6﹣a2+2a﹣1=5a2+15a+5,
故答案为5a2+15a+5.
11.解:∵代数式m2﹣km+1是一个完全平方式,
∴﹣k=±2×1=±2,
∴k=±2,
故答案为:±2.
12.解:∵多项式(x2+ax﹣1)(﹣2x3+x2)=﹣2x5+(1﹣2a)x4+(a+2)x3﹣x2不含x4项,
∴1﹣2a=0,
解得a.
故答案为:.
三、解答题
13.解:(1)20242﹣2023×2025
=20242﹣(2024﹣1)×(2024+1)
=20242﹣(20242﹣12)
=20242﹣20242+1
=1;
(2)186.72﹣2×186.7×86.7+86.72
=(186.7﹣86.7)2
=1002
=10000.
14.解:(1)S草坪=S长方形一S正方形=(5a+b)(2a+b)﹣(a+b)2=10a2+5ab+2ab+b2﹣a2﹣2ab﹣b2=9a2+5ab,
∴绿化面积为(9a2+5ab)平方米;
(2)当a=1,b=2时,
S草坪=9a2+5ab=9+10=19(平方米),
答:绿化面积为19平方米.
15.解:(1)(﹣2ab)(3a2﹣2ab﹣4b2)
=﹣6a3b+4a2b2+8ab3;
(2)(2x﹣1)(x﹣4)﹣(x+3)(x+2)
=2x2﹣8x﹣x+4﹣(x2+5x+6)
=2x2﹣9x+4﹣x2﹣5x﹣6
=x2﹣14x﹣2.
16.解:(1)∵甲错把b看成了6,
∴(2x+a)(x+6)=2x2+(12+a)x+6a,
又(2x+a)(x+6)=2x2+8x﹣24,
∴6a=﹣24,
∴a=﹣4.
∵乙错把a看成了﹣a,
∴(2x﹣a)(x+b)=2x2+(2b﹣a)x﹣ab,
又(2x﹣a)(x+b)=2x2+14x+20,
∴2b﹣a=14,
∵a=﹣4,
∴b=5.
故a=﹣4,b=5.
(2)由(1)得:(2x+a)(x+b)=(2x﹣4)(x+5)=2x2+6x﹣20.
17.解:(1)(ax﹣3)(2x+1)﹣4x2+m
=2ax2+ax﹣6x﹣3﹣4x2+m
=(2a﹣4)x2+(a﹣6)x+m﹣3,
∵化简后不含x2项和常数项,
∴2a﹣4=0,m﹣3=0,
解得:a=2,m=3;
(2)把a=2,m=3代入an+mn=﹣5,
∴2n+3n=﹣5,
∴n=﹣1,
∴﹣4n2+3m=﹣4×(﹣1)2+3×3=﹣4+9=5.
18.解:(1)根据图3可知,阴影部分的面积为两个正方形的面积和,即a2+b2,
∵大正方形的边长为(a+b),
∴大正方形的面积为(a+b)2,
∵两个空白矩形的面积和为2ab,
∴阴影部分的面积为(a+b)2﹣2ab,
故a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2=(a+b)2﹣2ab;
(2)∵a+b=8,ab=4,
∴a2+b2
=(a+b)2﹣2ab
=82﹣2×4
=64﹣8
=56;
(3)∵(9﹣x)+(x﹣4)=5,(9﹣x)(x﹣4)=2,
(9﹣x)2+(x﹣4)2
=[9﹣x+x﹣4]2﹣2(9﹣x)(x﹣4)
=52﹣2×2
=21;
(4)∵AC⊥BD,设AE=DE=p,BE=CE=q,
∴,,,,
∵种花区域的面积和为35,即,
∴p2+q2=70,
∵p+q=AE+CE=AC=11,
∴种草区域的面积和为S△CDE+S△ABE
=pq
=25.5.
19.解:(1)图1中,阴影部分可以看作两个正方形的面积差,即m2﹣n2,拼成长为(m+n),宽为(m﹣n)的长方形,因此面积为(m+n)(m﹣n),
因此m2﹣n2=(m+n)(m﹣n),
故选:C;
(2)设正方形ABCD的边长为a,正方形CEFG的边长为b,则S1=a2,S2=b2,
∵S1﹣S2=30,
∴a2﹣b2=30,
∴S不规则四边形BGED=S△BDG+S△EDG
=DG BC+DG CE
=DG (BC+CE)
=(a﹣b)(a+b)
=(a2﹣b2)
=×30
=15,
答:不规则四边形BGED的面积为15.
21世纪教育网(www.21cnjy.com)
第八章整式乘法章节期中复习苏科版2024—2025学年七年级下册
一、选择题
1.计算(a﹣b)(a+b)(a2+b2)(a4+b4)等于( )
A.a4﹣b4 B.a6+b6 C.a6﹣b6 D.a8﹣b8
2.若(x+2)(x﹣3)=x2+ax﹣6,则a的值为( )
A.﹣1 B.1 C.3 D.5
3.若a+b=0,ab=﹣11,则a2+b2的值是( )
A.﹣11 B.11 C.﹣22 D.22
4.下列运算正确的是( )
A.(﹣x﹣y)2=x2+2xy+y2 B.(﹣a﹣b) (a+b)=a2﹣b2
C.(m﹣3)(m+2)=m2﹣6 D.(a﹣b)2=a2﹣b2
5.下列整式乘法能用平方差公式计算的是( )
A.(2a+b)(a﹣2b) B.(b+2a)(2a﹣b)
C.(b﹣2a)(2a﹣b) D.(a﹣2b)(2b﹣a)
6.在下面的正方形分割方案中,可以验证(a+b)2=(a﹣b)2+4ab的图形是( )
A. B.
C. D.
7.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到a2+3ab+2b2=(a+2b)(a+b).若已知a2+b2+c2=69,ab+bc+ac=50,由图2所表示的数学等式,则a+b+c的值为( )
A.1 B.12 C.13 D.14
8.如图,在矩形ABCD中,AB=10,BC=5,点M和点N分别在AB和BC边上,并且AM﹣CN=1,分别以BM和BN为边向上、向右作正方形,两个正方形的面积分别为S1和S2,且S1+S2=50,则图中阴影部分的面积为( )
A.15 B.17
C.19 D.21
二、填空题
9.已知(m﹣n)2=32,(m+n)2=200,则m2+n2的值为 .
10.在长为(3a+2)、宽为(2a+3)的长方形铁皮上剪去一个边长为(a﹣1)的小正方形,则剩余部分的面积为 .
11.若代数式m2﹣km+1是一个完全平方式,则实数k= .
12.要使(x2+ax﹣1)(﹣2x3+x2)的展开式中不含x4项,则a的值为 .
三、解答题
13.简便运算:
(1)20242﹣2023×2025;
(2)186.72﹣2×186.7×86.7+86.72.
14.如图,某学校有一块长为(5a+b)m,宽为(2a+b)m的长方形土地,计划在阴影部分的区域进行绿化,中间修建一个边长为(a+b)m的正方形喷水池.
(1)用含a,b的代数式表示绿化面积;
(2)当a=1,b=2时,求绿化面积.
15.计算:
(1)(﹣2ab)(3a2﹣2ab﹣4b2);
(2)(2x﹣1)(x﹣4)﹣(x+3)(x+2).
16.在计算(2x+a)(x+b)时,甲错把b看成了6,得到的结果是2x2+8x﹣24,乙错把a看成了﹣a,得到的结果是2x2+14x+20.
(1)求a、b的值;
(2)求(2x+a)(x+b)的正确结果.
17.关于x的代数式(ax﹣3)(2x+1)﹣4x2+m化简后不含有x2项和常数项.
(1)求a和m的值.
(2)若an+mn=﹣5,求代数式﹣4n2+3m的值.
18.【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图(1),在边长为a的正方形中剪掉一个边长为b的小正方形,把余下的部分沿虚线剪开拼成一个长方形如图(2).图(1)中阴影部分面积可表示为a2﹣b2,图(2)中阴影部分面积可表示为(a+b)(a﹣b),因为两个图中的阴影部分面积是相同的,所以可得到等式:a2﹣b2=(a+b)(a﹣b).
【类比探究】(1)用两种不同方法表示图(3)中阴影部分面积,可得到一个关于a2+b2、(a+b)2、ab的等量关系式是 .
【实践运用】(2)根据(1)所得的关系式,若a+b=8,ab=4,则a2+b2= .
【拓展迁移】(3)若x满足(9﹣x)(x﹣4)=2,求(9﹣x)2+(x﹣4)2的值.
【灵活应用】(4)如图(4),某学校有一块梯形空地ABCD,AC⊥BD于点E,AE=DE,BE=CE.该校计划在△AED和△BEC区域内种花,在△CDE和△ABE的区域内种草,经测量种花区域的面积和为35,AC=11,求种草区域的面积和.
19.如图1,在边长为m的正方形纸片中剪去一个边长为n的小正方形纸片(m>n),把剩余的部分拼成一个长方形纸片.
(1)通过计算两个纸片中阴影部分的面积,可得等式 .(填选项前面的字母)
A.m2+2mn+n2=(m+n)2
B.m2﹣2mn+n2=(m﹣n)2
C.m2﹣n2=(m+n)(m﹣n)
D.m2﹣mn=m(m﹣n)
(2)请利用(1)中所选的结论,解答以下问题:如图2,大正方形ABCD的面积为S1,小正方形CEFG的面积为S2,且S1﹣S2=30,求不规则四边形BGED的面积.
参考答案
一、选择题
1.解:(a﹣b)(a+b)(a2+b2)(a4+b4)
=(a2﹣b2)(a2+b2)(a4+b4)
=(a4﹣b4)(a4+b4)
=a8﹣b8,
故选:D.
2.解:(x+2)(x﹣3)
=x2﹣3x+2x﹣6
=x2﹣x﹣6,
∵(x+2)(x﹣3)=x2+ax﹣6,
∴a=﹣1,
故选:A.
3.解:由条件可知(a+b)2=a2+b2+2ab=0,
∵ab=﹣11,
∴a2+b2+2×(﹣11)=0,
∴a2+b2=22,
故选:D.
4.解:A、(﹣x﹣y)2=x2+2xy+y2,正确;
B、(﹣a﹣b) (a+b)=﹣a2﹣b2﹣2ab,错误;
C、(m﹣3)(m+2)=m2﹣m﹣6,错误;
D、(a﹣b)2=a2+b2﹣2ab,错误,
故选:A.
5.解:(2a+b)(a﹣2b)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则A不符合题意,
(b+2a)(2a﹣b)是两式的和与相同两式的差的积,它能用平方差公式计算,则B符合题意,
(b﹣2a)(2a﹣b)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则C不符合题意,
(a﹣2b)(2b﹣a)不是两式的和与相同两式的差的积,它不能用平方差公式计算,则D不符合题意,
故选:B.
6.解:∵由选项A可得a2﹣b2=(a+b)(a﹣b),
∴选项A不符合题意;
∵由选项B可得(a+b)2=a2+2ab+b2,
∴选项B不符合题意;
∵由选项C可得(a﹣b)2=a2﹣2ab+b2.
∴选项C不符合题意;
∵由选项D可得(a+b)2=(a﹣b)2+4ab,
∴选项D符合题意;
故选:D.
7.解:由图2可得(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
∴(a+b+c)2=a2+b2+c2+2(ab+bc+ac)=69+2×50=169,
又∵a+b+c>0,
∴a+b+c=13,
故选:C.
8.解:设AM=x,则CN=x﹣1,
∴BM=AB﹣AM=10﹣x,BN=5﹣(x﹣1)=6﹣x,
∵S1+S2=50,
∴(10﹣x)2+(6﹣x)2=50,
∴x=8或x=8(不合题意舍去),
∴,BN2,
∴图中阴影部分的面积为BM BN17,
故选:B.
二、填空题
9.解:(m﹣n)2=m2﹣2mn+n2=32①,
(m+n)2=m2+2mn+n2=200②,
②+①得,2m2+2n2=232,
解得:m2+n2=116.
故答案为:116.
10.解:根据题意得:(3a+2)(2a+3)﹣(a﹣1)2=6a2+9a+4a+6﹣a2+2a﹣1=5a2+15a+5,
故答案为5a2+15a+5.
11.解:∵代数式m2﹣km+1是一个完全平方式,
∴﹣k=±2×1=±2,
∴k=±2,
故答案为:±2.
12.解:∵多项式(x2+ax﹣1)(﹣2x3+x2)=﹣2x5+(1﹣2a)x4+(a+2)x3﹣x2不含x4项,
∴1﹣2a=0,
解得a.
故答案为:.
三、解答题
13.解:(1)20242﹣2023×2025
=20242﹣(2024﹣1)×(2024+1)
=20242﹣(20242﹣12)
=20242﹣20242+1
=1;
(2)186.72﹣2×186.7×86.7+86.72
=(186.7﹣86.7)2
=1002
=10000.
14.解:(1)S草坪=S长方形一S正方形=(5a+b)(2a+b)﹣(a+b)2=10a2+5ab+2ab+b2﹣a2﹣2ab﹣b2=9a2+5ab,
∴绿化面积为(9a2+5ab)平方米;
(2)当a=1,b=2时,
S草坪=9a2+5ab=9+10=19(平方米),
答:绿化面积为19平方米.
15.解:(1)(﹣2ab)(3a2﹣2ab﹣4b2)
=﹣6a3b+4a2b2+8ab3;
(2)(2x﹣1)(x﹣4)﹣(x+3)(x+2)
=2x2﹣8x﹣x+4﹣(x2+5x+6)
=2x2﹣9x+4﹣x2﹣5x﹣6
=x2﹣14x﹣2.
16.解:(1)∵甲错把b看成了6,
∴(2x+a)(x+6)=2x2+(12+a)x+6a,
又(2x+a)(x+6)=2x2+8x﹣24,
∴6a=﹣24,
∴a=﹣4.
∵乙错把a看成了﹣a,
∴(2x﹣a)(x+b)=2x2+(2b﹣a)x﹣ab,
又(2x﹣a)(x+b)=2x2+14x+20,
∴2b﹣a=14,
∵a=﹣4,
∴b=5.
故a=﹣4,b=5.
(2)由(1)得:(2x+a)(x+b)=(2x﹣4)(x+5)=2x2+6x﹣20.
17.解:(1)(ax﹣3)(2x+1)﹣4x2+m
=2ax2+ax﹣6x﹣3﹣4x2+m
=(2a﹣4)x2+(a﹣6)x+m﹣3,
∵化简后不含x2项和常数项,
∴2a﹣4=0,m﹣3=0,
解得:a=2,m=3;
(2)把a=2,m=3代入an+mn=﹣5,
∴2n+3n=﹣5,
∴n=﹣1,
∴﹣4n2+3m=﹣4×(﹣1)2+3×3=﹣4+9=5.
18.解:(1)根据图3可知,阴影部分的面积为两个正方形的面积和,即a2+b2,
∵大正方形的边长为(a+b),
∴大正方形的面积为(a+b)2,
∵两个空白矩形的面积和为2ab,
∴阴影部分的面积为(a+b)2﹣2ab,
故a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2=(a+b)2﹣2ab;
(2)∵a+b=8,ab=4,
∴a2+b2
=(a+b)2﹣2ab
=82﹣2×4
=64﹣8
=56;
(3)∵(9﹣x)+(x﹣4)=5,(9﹣x)(x﹣4)=2,
(9﹣x)2+(x﹣4)2
=[9﹣x+x﹣4]2﹣2(9﹣x)(x﹣4)
=52﹣2×2
=21;
(4)∵AC⊥BD,设AE=DE=p,BE=CE=q,
∴,,,,
∵种花区域的面积和为35,即,
∴p2+q2=70,
∵p+q=AE+CE=AC=11,
∴种草区域的面积和为S△CDE+S△ABE
=pq
=25.5.
19.解:(1)图1中,阴影部分可以看作两个正方形的面积差,即m2﹣n2,拼成长为(m+n),宽为(m﹣n)的长方形,因此面积为(m+n)(m﹣n),
因此m2﹣n2=(m+n)(m﹣n),
故选:C;
(2)设正方形ABCD的边长为a,正方形CEFG的边长为b,则S1=a2,S2=b2,
∵S1﹣S2=30,
∴a2﹣b2=30,
∴S不规则四边形BGED=S△BDG+S△EDG
=DG BC+DG CE
=DG (BC+CE)
=(a﹣b)(a+b)
=(a2﹣b2)
=×30
=15,
答:不规则四边形BGED的面积为15.
21世纪教育网(www.21cnjy.com)
同课章节目录
