第十八章平行四边形章节期中复习(含解析)
文档属性
| 名称 | 第十八章平行四边形章节期中复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 518.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形章节期中复习人教版2024—2025学年八年级下册
一、选择题
1.如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
6.如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
8.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣3),则点A的坐标为 .
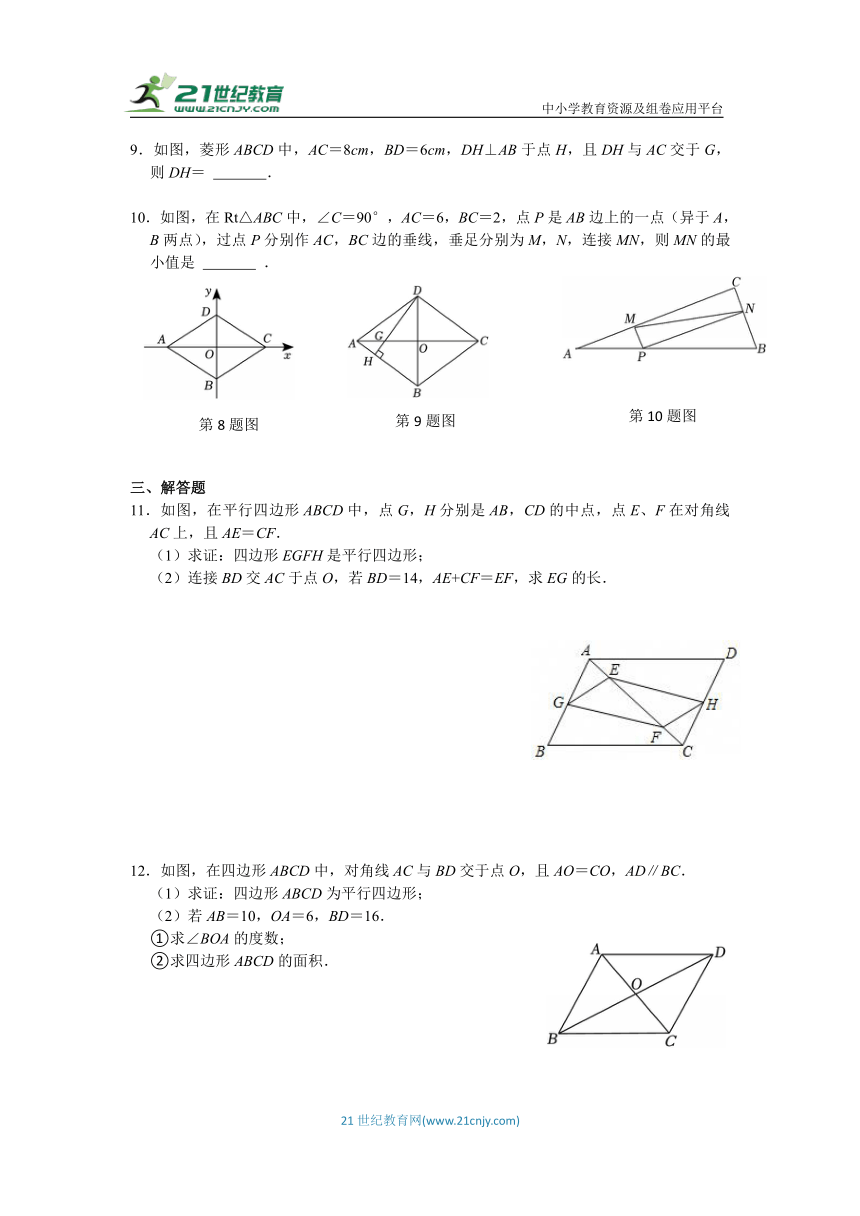
9.如图,菱形ABCD中,AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH= .
10.如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
三、解答题
11.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
12.如图,在四边形ABCD中,对角线AC与BD交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
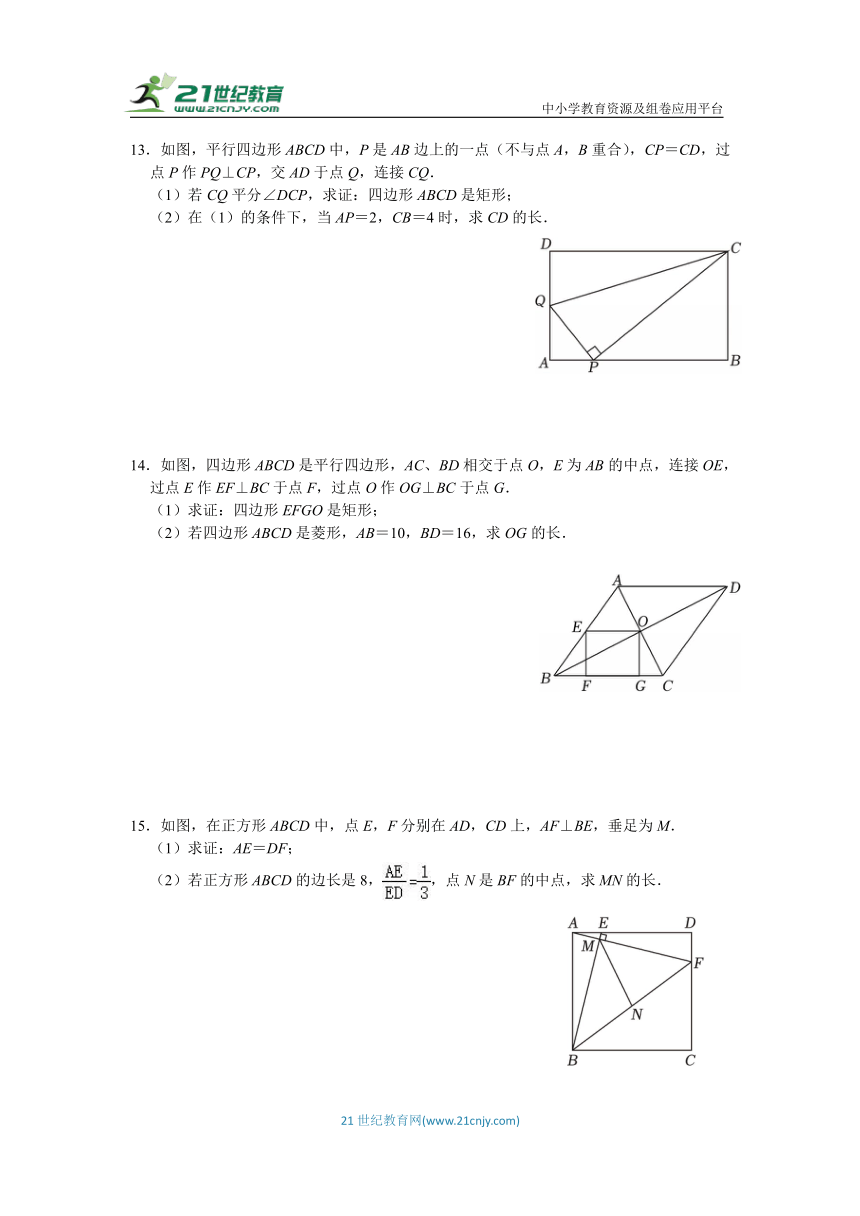
13.如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
14.如图,四边形ABCD是平行四边形,AC、BD相交于点O,E为AB的中点,连接OE,过点E作EF⊥BC于点F,过点O作OG⊥BC于点G.
(1)求证:四边形EFGO是矩形;
(2)若四边形ABCD是菱形,AB=10,BD=16,求OG的长.
15.如图,在正方形ABCD中,点E,F分别在AD,CD上,AF⊥BE,垂足为M.
(1)求证:AE=DF;
(2)若正方形ABCD的边长是8,,点N是BF的中点,求MN的长.
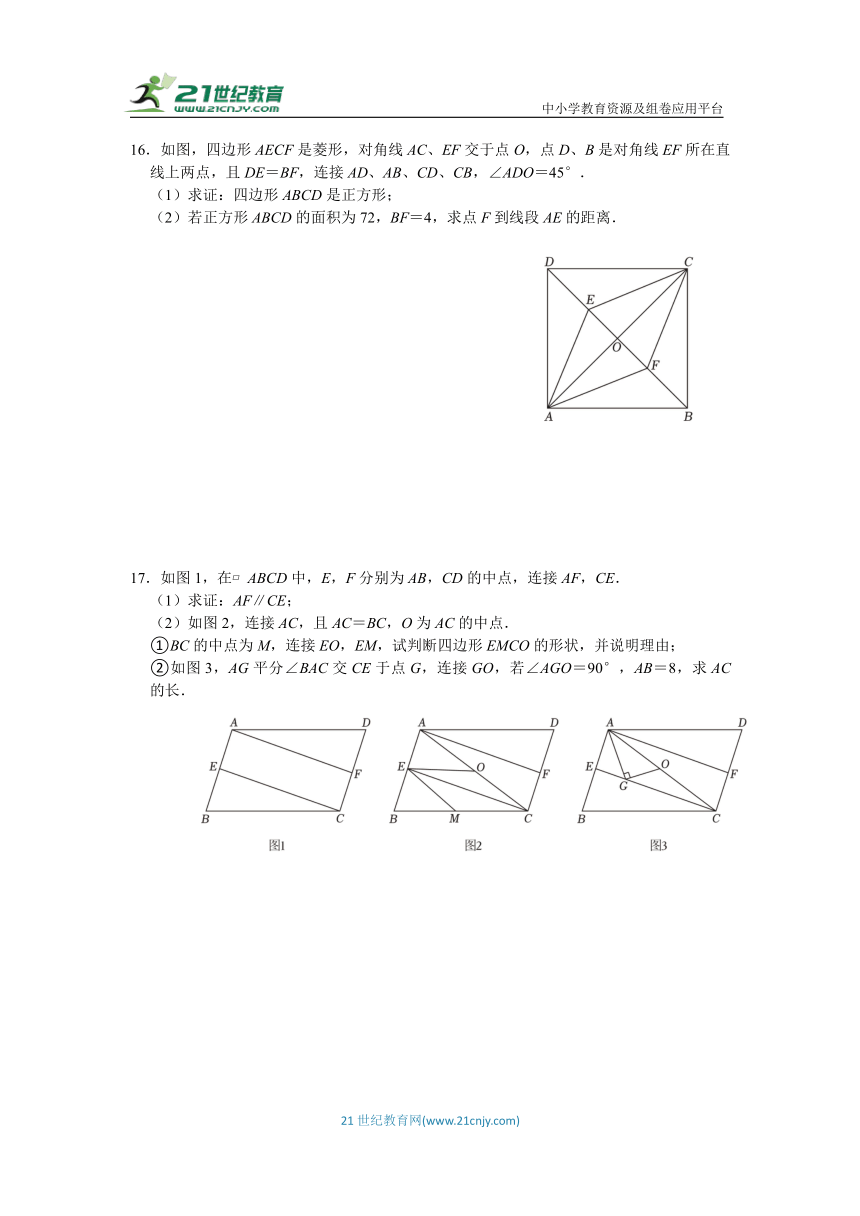
16.如图,四边形AECF是菱形,对角线AC、EF交于点O,点D、B是对角线EF所在直线上两点,且DE=BF,连接AD、AB、CD、CB,∠ADO=45°.
(1)求证:四边形ABCD是正方形;
(2)若正方形ABCD的面积为72,BF=4,求点F到线段AE的距离.
17.如图1,在 ABCD中,E,F分别为AB,CD的中点,连接AF,CE.
(1)求证:AF∥CE;
(2)如图2,连接AC,且AC=BC,O为AC的中点.
①BC的中点为M,连接EO,EM,试判断四边形EMCO的形状,并说明理由;
②如图3,AG平分∠BAC交CE于点G,连接GO,若∠AGO=90°,AB=8,求AC的长.
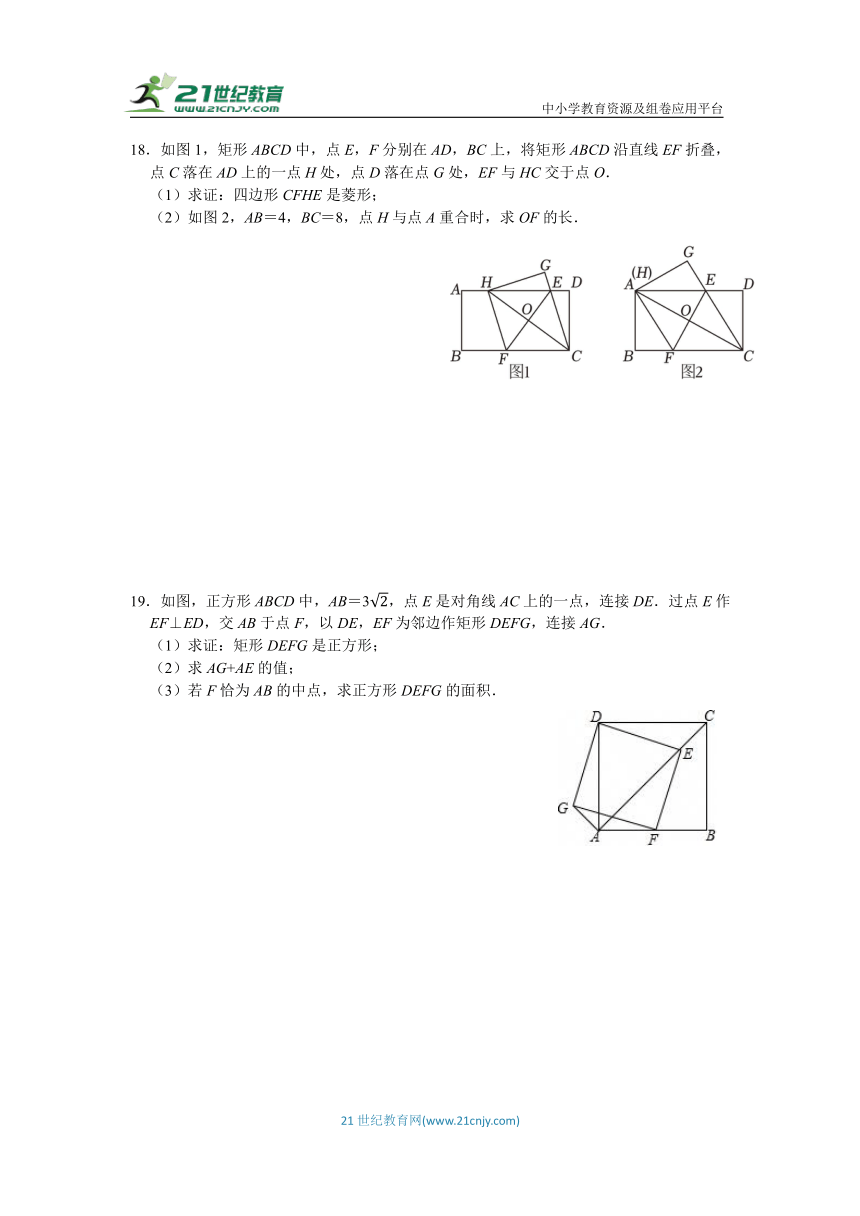
18.如图1,矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,EF与HC交于点O.
(1)求证:四边形CFHE是菱形;
(2)如图2,AB=4,BC=8,点H与点A重合时,求OF的长.
19.如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB的中点,求正方形DEFG的面积.
参考答案
一、选择题
1.【解答】解:A、∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、由AB∥DC,AD=BC,不能判定四边形ABCD是平行四边形,故选项C符合题意;
D、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故选项D不符合题意;
故选:C.
2.【解答】解:∵矩形的性质为:对边平行且相等,四个角都相等,对角线互相平分且相等,有两条对称轴,
菱形的性质为:四边相等,对边平行且相等,对角相等,对角线互相垂直平分,有两条对称轴,
∴菱形和矩形都具有的性质是:对边平行且相等,对角线互相平分,有两条对称轴,
故选:C.
3.【解答】解:A、对角线互相平分、垂直且相等的四边形是正方形,错误;
B、对角线互相平分、垂直的四边形是菱形,错误;
C、对角线互相平分的四边形是平行四边形,错误;
D、对角线相等的平行四边形是矩形,正确;
故选:D.
4.【解答】解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC,
∵∠ABD=∠CBD,
∴∠BDC=∠CBD,
∴BC=CD,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误,不符合题意;
B、∵∠ABC=90°,
∴平行四边形ABCD是矩形,故本选项正确,符合题意;
C、∵四边形ABCD是平行四边形,
∴当AC⊥BD时四边形ABCD是菱形,故本选项错误,不符合题意;
D、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误,不符合题意,不符合题意;
故选:B.
5.【解答】解:∵四边形ABCD是菱形,
∴AO=AC,BO=DB,AC⊥BD,AB=CB=CD=AD,
∵AC=8cm,BD=6cm,
∴AO=4cm,BO=3cm,
∴AB==5cm,
∴菱形ABCD的周长是:5cm×4=20cm,
故选:B.
6.【解答】解:因为一般四边形的中点四边形是平行四边形,
当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形,
故④选项正确,
故选:A.
二、填空题
7.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
8.【解答】解:四边形ABCD是菱形,∠ABC=120°,
∴,
∴∠BAO=30°,
∴AB=2OB,
∵点B的坐标为(0,﹣3),
∴OB=3,
∴AB=2OB=6,
∴,
∴点A的坐标为,
故答案为:.
9.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC8=4(cm),OB=ODBD6=3(cm),
在Rt△AOB中,由勾股定理得:AB5(cm),
∵S菱形ABCDAC BD=AB DH,
∴DH(cm),
故答案为:cm.
10.【解答】解:如图,连接PC.
在△ABC中,∠C=90°,AC=6,BC=2,
∴AB2,
∵PM⊥AC,PN⊥BC,
∴∠PMC=∠PNC=∠C=90°,
∴四边形PMCN是矩形,
∴MN=PC,
当PC⊥AB时,PC的值最小,
此时PC的最小值,
∴MN的最小值为,
故答案为:.
三、解答题
11.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB.
12.【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形;
(2)解:①∵BD=16,
OB=OD=8,
∵AB=10,OA=6,
∴AB2=OA2+OB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,∠BOA=90°,
∴BD⊥AC,
∵OA=6,
∴AC=12,
∴S四边形ABCDBD AC16×12=96.
13.【解答】(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∵EF⊥BC,OG⊥BC,
∴EF∥OG,∠EFG=90°,
∴四边形EFGO是平行四边形,
又∵∠EFG=90°,
∴平行四边形EFGO是矩形;
(2)解:∵四边形ABCD是菱形,BD=16,
∴BC=AB=10,OA=OC,OB=ODBD=8,AC⊥BD,
∴∠BOC=90°,
∴OC6,
由(1)可知,四边形EFGO是矩形,
∴∠OGF=90°,
∴OG⊥BC,
∴S△OBCBC OGOB OC,
∴OG4.8,
即OG的长为4.8.
15.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠BAE=∠ADF=90°,
∵AF⊥BE,
∴∠DAF+∠AEM=90°,
∵∠AEM+∠ABE=90°,
∴∠DAF=∠ABE,
∴△ABE≌△DAF(ASA),
∴AE=DF;
(2)解:∵,
∴ED=3AE,
∴AD=4AE=8,
∴AE=2=DF,
∴CF=6,
∴BF==10,
∵N是中点,∠BMF=90°,
∴MN==5.
16.【解答】(1)证明:∵菱形AECF的对角线AC和EF交于点O,
∴AC⊥EF,OA=OC,OE=OF,
∵BE=DF,
∴BO=DO,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∵∠ADO=45°,
∴∠DAO=∠ADO=45°,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是正方形;
(2)解:∵正方形ABCD的面积为72,
∴AC BD=72,
∴×4BO2=72,
∴BO=DO=CO=AO=6,
∴AC=12,
∵BF=4,
∴OF=2,
∵四边形ABCD是菱形,
∴EF=2EO=2OF=4,AC⊥EF,
∴菱形AFCE的面积=AC EF=24,
在Rt△AOE中,AE==2,
设点F到线段AE的距离为h,
∴AE h=24,
即2h=24,
∴h=.
即点F到线段AE的距离为.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E,F分别为AB,CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE;
(2)解:①四边形EMCO为菱形.理由:
∵O为AC的中点,E为AB的中点,
∴OE为△ABC的中位线,
∴OE∥BC,OE=BC.
∵E为AB的中点,BC的中点为M,
∴EM∥AC,EM=AC,
∴四边形EMCO为平行四边形.
∵AC=BC,
∴EO=EM,
∴四边形EMCO为菱形.
②过点O作OH⊥EC于点H,过点G作GM⊥AC于点M,如图,
∵AC=BC,E为AB的中点,
∴CE⊥AB,AE=AB=4.
∵AG平分∠BAC交CE于点G,
∴∠GAE=∠GAC,
∵GM⊥AC,GE⊥AB,
∴GE=GM.
在Rt△AEG和Rt△AMG中,
,
∴Rt△AEG≌Rt△AMG(HL),
∴AE=AM=4.
∵CE⊥AE,OH⊥EC,
∴OH∥AE,
∵O为AC的中点,
∴OH=AE=2.
∵∠AGO=90°,
∴∠AGE+∠OGC=90°,∠AGM+∠OGM=90°,
∵Rt△AEG≌Rt△AMG,
∴∠AGE=∠AGM,
∴∠OGM=∠OGH,
∵OM⊥GM,OH⊥GH,
∴OM=OH=2,
∴OA=AM+OM=6,
∵O为AC的中点,
∴AC=2OA=12.
18.【解答】(1)证明:在矩形ABCD中,AD∥BC,
即HE∥CF,
∴∠HEF=∠EFC,
由翻折可知:∠EFC=∠HFE,
∴∠HEF=∠HFE,
∴HE=HF,
∵FC=FH,
∴HE=CF,
∵EH∥CF,
∴四边形CFHE是平行四边形,
∵CF=FH,
∴四边形CFHE是菱形;
(2)解:点H与点A重合时,设BF=x,则AF=FC=BC﹣BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
∴CE=AF=8﹣x=5,
∵CD=AB=4,
∴DE===3,
如图,过点F作FM⊥AD于M,得矩形ABFM,矩形CDMF,
∴AM=BF,DM=CF,MF=AB=4,
∴ME=8﹣3﹣3=2,
由勾股定理得,EF===2,
∴OF=EF=.
19.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=3,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=6;
(3)解:连接DF,
∵四边形ABCD是正方形,
∴AB=AD=3,AB∥CD,
∵F是AB中点,
∴AF=FB,
∴DF,
∴正方形DEFG的面积DF2()2.
21世纪教育网(www.21cnjy.com)
第十八章平行四边形章节期中复习人教版2024—2025学年八年级下册
一、选择题
1.如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
6.如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
7.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
8.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣3),则点A的坐标为 .
9.如图,菱形ABCD中,AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH= .
10.如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
三、解答题
11.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
12.如图,在四边形ABCD中,对角线AC与BD交于点O,且AO=CO,AD∥BC.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=10,OA=6,BD=16.
①求∠BOA的度数;
②求四边形ABCD的面积.
13.如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
14.如图,四边形ABCD是平行四边形,AC、BD相交于点O,E为AB的中点,连接OE,过点E作EF⊥BC于点F,过点O作OG⊥BC于点G.
(1)求证:四边形EFGO是矩形;
(2)若四边形ABCD是菱形,AB=10,BD=16,求OG的长.
15.如图,在正方形ABCD中,点E,F分别在AD,CD上,AF⊥BE,垂足为M.
(1)求证:AE=DF;
(2)若正方形ABCD的边长是8,,点N是BF的中点,求MN的长.
16.如图,四边形AECF是菱形,对角线AC、EF交于点O,点D、B是对角线EF所在直线上两点,且DE=BF,连接AD、AB、CD、CB,∠ADO=45°.
(1)求证:四边形ABCD是正方形;
(2)若正方形ABCD的面积为72,BF=4,求点F到线段AE的距离.
17.如图1,在 ABCD中,E,F分别为AB,CD的中点,连接AF,CE.
(1)求证:AF∥CE;
(2)如图2,连接AC,且AC=BC,O为AC的中点.
①BC的中点为M,连接EO,EM,试判断四边形EMCO的形状,并说明理由;
②如图3,AG平分∠BAC交CE于点G,连接GO,若∠AGO=90°,AB=8,求AC的长.
18.如图1,矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,EF与HC交于点O.
(1)求证:四边形CFHE是菱形;
(2)如图2,AB=4,BC=8,点H与点A重合时,求OF的长.
19.如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB的中点,求正方形DEFG的面积.
参考答案
一、选择题
1.【解答】解:A、∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、由AB∥DC,AD=BC,不能判定四边形ABCD是平行四边形,故选项C符合题意;
D、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故选项D不符合题意;
故选:C.
2.【解答】解:∵矩形的性质为:对边平行且相等,四个角都相等,对角线互相平分且相等,有两条对称轴,
菱形的性质为:四边相等,对边平行且相等,对角相等,对角线互相垂直平分,有两条对称轴,
∴菱形和矩形都具有的性质是:对边平行且相等,对角线互相平分,有两条对称轴,
故选:C.
3.【解答】解:A、对角线互相平分、垂直且相等的四边形是正方形,错误;
B、对角线互相平分、垂直的四边形是菱形,错误;
C、对角线互相平分的四边形是平行四边形,错误;
D、对角线相等的平行四边形是矩形,正确;
故选:D.
4.【解答】解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC,
∵∠ABD=∠CBD,
∴∠BDC=∠CBD,
∴BC=CD,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误,不符合题意;
B、∵∠ABC=90°,
∴平行四边形ABCD是矩形,故本选项正确,符合题意;
C、∵四边形ABCD是平行四边形,
∴当AC⊥BD时四边形ABCD是菱形,故本选项错误,不符合题意;
D、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误,不符合题意,不符合题意;
故选:B.
5.【解答】解:∵四边形ABCD是菱形,
∴AO=AC,BO=DB,AC⊥BD,AB=CB=CD=AD,
∵AC=8cm,BD=6cm,
∴AO=4cm,BO=3cm,
∴AB==5cm,
∴菱形ABCD的周长是:5cm×4=20cm,
故选:B.
6.【解答】解:因为一般四边形的中点四边形是平行四边形,
当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形,
故④选项正确,
故选:A.
二、填空题
7.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
8.【解答】解:四边形ABCD是菱形,∠ABC=120°,
∴,
∴∠BAO=30°,
∴AB=2OB,
∵点B的坐标为(0,﹣3),
∴OB=3,
∴AB=2OB=6,
∴,
∴点A的坐标为,
故答案为:.
9.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC8=4(cm),OB=ODBD6=3(cm),
在Rt△AOB中,由勾股定理得:AB5(cm),
∵S菱形ABCDAC BD=AB DH,
∴DH(cm),
故答案为:cm.
10.【解答】解:如图,连接PC.
在△ABC中,∠C=90°,AC=6,BC=2,
∴AB2,
∵PM⊥AC,PN⊥BC,
∴∠PMC=∠PNC=∠C=90°,
∴四边形PMCN是矩形,
∴MN=PC,
当PC⊥AB时,PC的值最小,
此时PC的最小值,
∴MN的最小值为,
故答案为:.
三、解答题
11.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB.
12.【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴OB=OD,
∵OA=OC,
∴四边形ABCD为平行四边形;
(2)解:①∵BD=16,
OB=OD=8,
∵AB=10,OA=6,
∴AB2=OA2+OB2,
∴△AOB是直角三角形,
∴∠BOA=90°;
②由①可知,∠BOA=90°,
∴BD⊥AC,
∵OA=6,
∴AC=12,
∴S四边形ABCDBD AC16×12=96.
13.【解答】(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∵EF⊥BC,OG⊥BC,
∴EF∥OG,∠EFG=90°,
∴四边形EFGO是平行四边形,
又∵∠EFG=90°,
∴平行四边形EFGO是矩形;
(2)解:∵四边形ABCD是菱形,BD=16,
∴BC=AB=10,OA=OC,OB=ODBD=8,AC⊥BD,
∴∠BOC=90°,
∴OC6,
由(1)可知,四边形EFGO是矩形,
∴∠OGF=90°,
∴OG⊥BC,
∴S△OBCBC OGOB OC,
∴OG4.8,
即OG的长为4.8.
15.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠BAE=∠ADF=90°,
∵AF⊥BE,
∴∠DAF+∠AEM=90°,
∵∠AEM+∠ABE=90°,
∴∠DAF=∠ABE,
∴△ABE≌△DAF(ASA),
∴AE=DF;
(2)解:∵,
∴ED=3AE,
∴AD=4AE=8,
∴AE=2=DF,
∴CF=6,
∴BF==10,
∵N是中点,∠BMF=90°,
∴MN==5.
16.【解答】(1)证明:∵菱形AECF的对角线AC和EF交于点O,
∴AC⊥EF,OA=OC,OE=OF,
∵BE=DF,
∴BO=DO,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∵∠ADO=45°,
∴∠DAO=∠ADO=45°,
∴AO=DO,
∴AC=BD,
∴四边形ABCD是正方形;
(2)解:∵正方形ABCD的面积为72,
∴AC BD=72,
∴×4BO2=72,
∴BO=DO=CO=AO=6,
∴AC=12,
∵BF=4,
∴OF=2,
∵四边形ABCD是菱形,
∴EF=2EO=2OF=4,AC⊥EF,
∴菱形AFCE的面积=AC EF=24,
在Rt△AOE中,AE==2,
设点F到线段AE的距离为h,
∴AE h=24,
即2h=24,
∴h=.
即点F到线段AE的距离为.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E,F分别为AB,CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE;
(2)解:①四边形EMCO为菱形.理由:
∵O为AC的中点,E为AB的中点,
∴OE为△ABC的中位线,
∴OE∥BC,OE=BC.
∵E为AB的中点,BC的中点为M,
∴EM∥AC,EM=AC,
∴四边形EMCO为平行四边形.
∵AC=BC,
∴EO=EM,
∴四边形EMCO为菱形.
②过点O作OH⊥EC于点H,过点G作GM⊥AC于点M,如图,
∵AC=BC,E为AB的中点,
∴CE⊥AB,AE=AB=4.
∵AG平分∠BAC交CE于点G,
∴∠GAE=∠GAC,
∵GM⊥AC,GE⊥AB,
∴GE=GM.
在Rt△AEG和Rt△AMG中,
,
∴Rt△AEG≌Rt△AMG(HL),
∴AE=AM=4.
∵CE⊥AE,OH⊥EC,
∴OH∥AE,
∵O为AC的中点,
∴OH=AE=2.
∵∠AGO=90°,
∴∠AGE+∠OGC=90°,∠AGM+∠OGM=90°,
∵Rt△AEG≌Rt△AMG,
∴∠AGE=∠AGM,
∴∠OGM=∠OGH,
∵OM⊥GM,OH⊥GH,
∴OM=OH=2,
∴OA=AM+OM=6,
∵O为AC的中点,
∴AC=2OA=12.
18.【解答】(1)证明:在矩形ABCD中,AD∥BC,
即HE∥CF,
∴∠HEF=∠EFC,
由翻折可知:∠EFC=∠HFE,
∴∠HEF=∠HFE,
∴HE=HF,
∵FC=FH,
∴HE=CF,
∵EH∥CF,
∴四边形CFHE是平行四边形,
∵CF=FH,
∴四边形CFHE是菱形;
(2)解:点H与点A重合时,设BF=x,则AF=FC=BC﹣BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
∴CE=AF=8﹣x=5,
∵CD=AB=4,
∴DE===3,
如图,过点F作FM⊥AD于M,得矩形ABFM,矩形CDMF,
∴AM=BF,DM=CF,MF=AB=4,
∴ME=8﹣3﹣3=2,
由勾股定理得,EF===2,
∴OF=EF=.
19.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=3,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=6;
(3)解:连接DF,
∵四边形ABCD是正方形,
∴AB=AD=3,AB∥CD,
∵F是AB中点,
∴AF=FB,
∴DF,
∴正方形DEFG的面积DF2()2.
21世纪教育网(www.21cnjy.com)
同课章节目录
