18.2特殊平行四边形期中复习(含解析)
文档属性
| 名称 | 18.2特殊平行四边形期中复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 595.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2特殊平行四边形期中复习人教版2024—2025学年八年级下册
一、选择题
1.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=10,则CD=( )
A.10 B.6 C.8 D.5
2.如图, ABCD的对角线AC、BD相交于点O,添加一个条件,使得 ABCD是菱形,则下列选项不符合题意的是( )
A.AC=BD B.AC⊥BD C.AB=BC D.∠ABD=∠CBD
3.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
4.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
5.如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
6.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
7.下列说法正确的是( )
A.对角线互相垂直的平行四边形是正方形
B.一组对边平行另一组对边相等的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线互相垂直的四边形是菱形
8.如图,在Rt△ABC中,∠ACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点Q,若HF=FG,则的值是( )
A. B. C. D.
9.如图,点M是正方形ABCD边AB上一点,DN⊥CM于N,DN=2CN=2,则BN的长度为( )
A.2 B. C. D.
二、填空题
10.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD中点,OE=4,则菱形ABCD的周长为 .
11.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:
(1)△DOF≌△COE;
(2)CF=BE;
(3)四边形CEOF的面积为正方形ABCD面积的;
(4)OF2+OE2=EF2.其中正确的是 .
12.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
三、解答题
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
15.如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
16.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
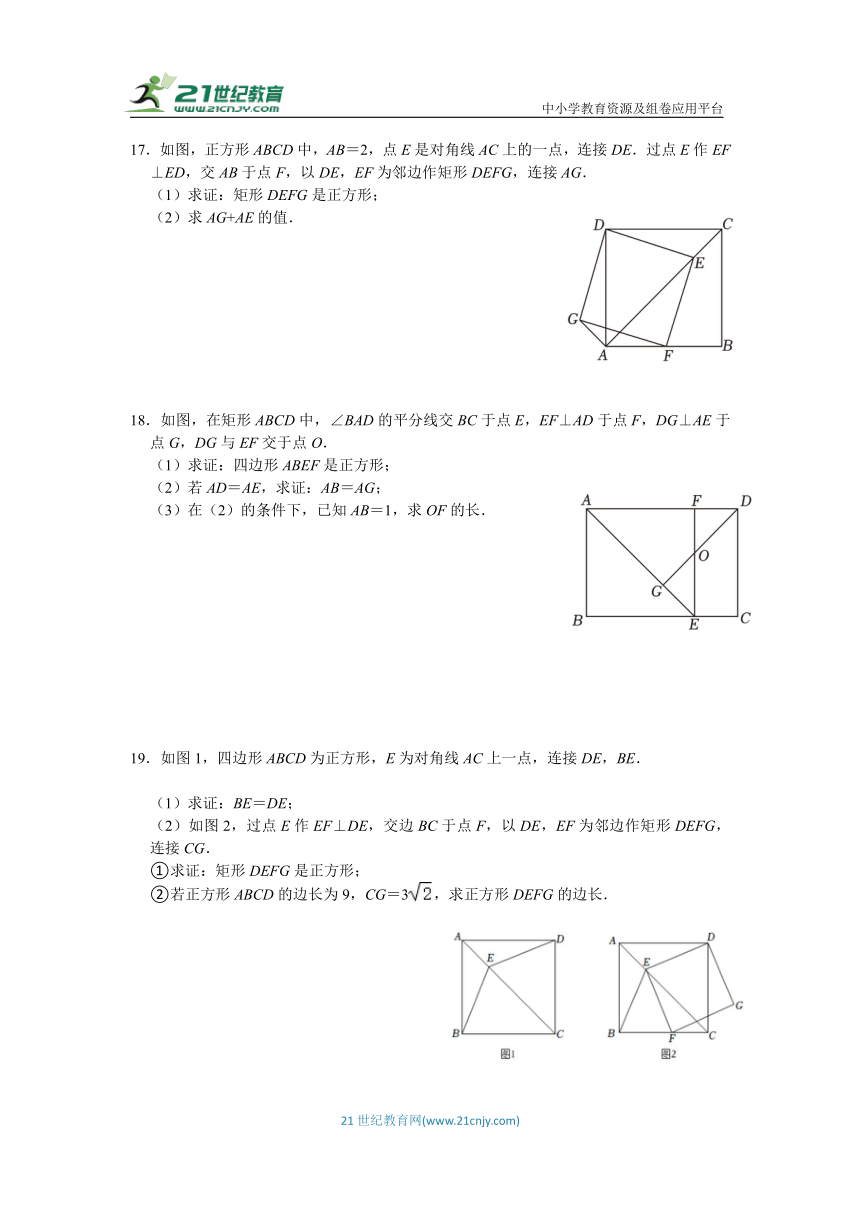
17.如图,正方形ABCD中,AB=2,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值.
18.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
19.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
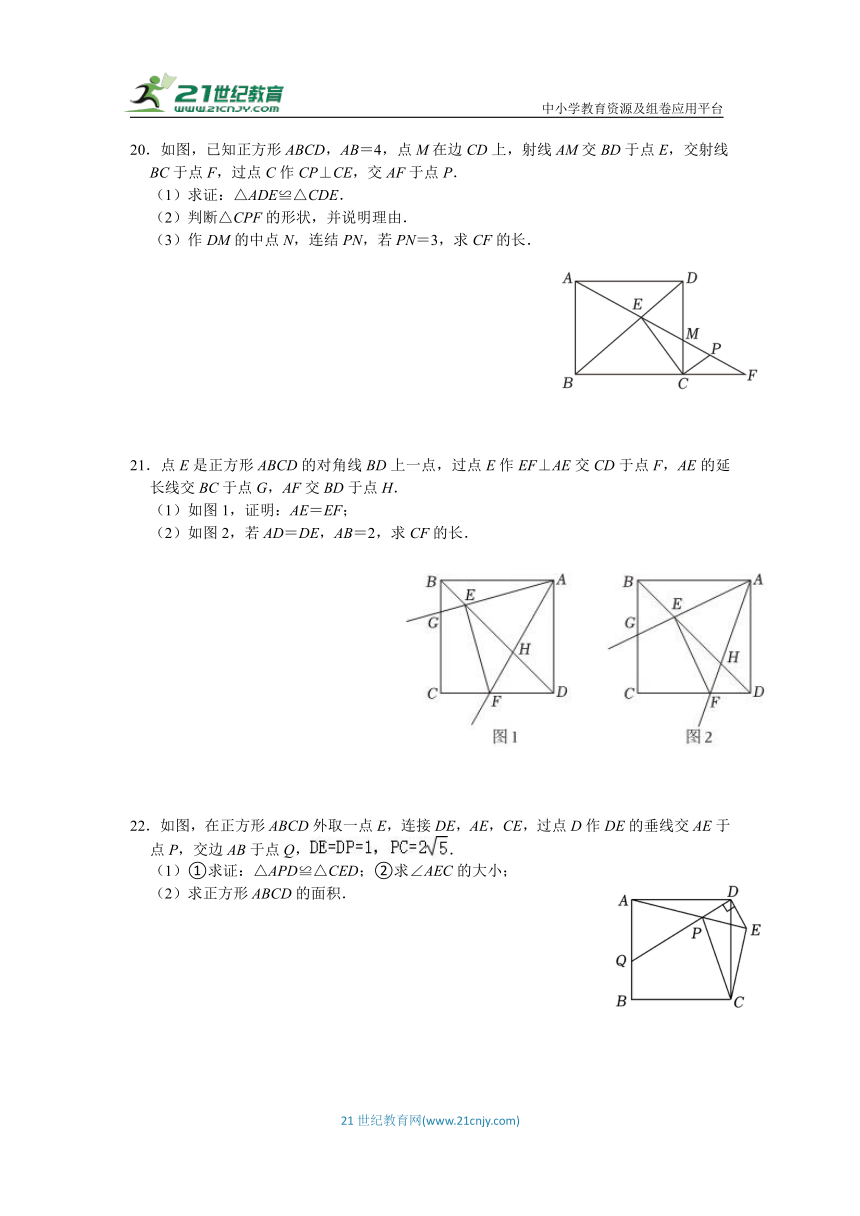
20.如图,已知正方形ABCD,AB=4,点M在边CD上,射线AM交BD于点E,交射线BC于点F,过点C作CP⊥CE,交AF于点P.
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连结PN,若PN=3,求CF的长.
21.点E是正方形ABCD的对角线BD上一点,过点E作EF⊥AE交CD于点F,AE的延长线交BC于点G,AF交BD于点H.
(1)如图1,证明:AE=EF;
(2)如图2,若AD=DE,AB=2,求CF的长.
22.如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,交边AB于点Q,.
(1)①求证:△APD≌△CED;②求∠AEC的大小;
(2)求正方形ABCD的面积.
23.已知正方形ABCD中,AB=3,且E为CD上的一动点,以AE为边作正方形AGFE,如图1所示,连接BE、GD.
(1)求证:BE=GD.
(2)如图2,延长GD、BE交于点Q,求证:BE⊥GD.
(3)若∠QED=60°,则DE的值是多少?
24.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH;
(2)求证:四边形AKFH是正方形;
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
参考答案
一、选择题
1.【解答】解:∵在Rt△ABC中,CD是斜边AB上的中线,且AB=10,
∴,
故选:D.
2.【解答】解:∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,但四边形ABCD不一定是菱形,
故A选项不符合题意;
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
故B选项符合题意;
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
故C选项符合题意;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴四边形ABCD是菱形,
故D选项符合题意,
故选:A.
3.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不符合题意;
B、是对角线相等,可推出平行四边形ABCD是矩形,故符合题意;
C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不符合题意;
D、无法判断.
故选:B.
4.【解答】解:A、对角线AC与BD互相垂直,AC=BD时,无法得出四边形ABCD是矩形,故此选项不合题意;
B、当AB=AD,CB=CD时,无法得到,四边形ABCD是菱形,故此选项不合题意;
C、当两条对角线AC与BD互相垂直,AB=AD=BC时,∴BO=DO,AO=CO,
∴四边形ABCD是平行四边形,
∵两条对角线AC与BD互相垂直,
∴平行四边形ABCD是菱形,故此选项正确;
D、当AC=BD,AD=AB时,无法得到四边形ABCD是正方形,故此选项不合题意;
故选:C.
5.【解答】解:∵四边形ABCD是菱形,CD=5,BD=8,
∴BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,
∴∠BOC=90°,
在Rt△OBC中,由勾股定理得:OC===3,
∴AC=2OC=6,
∵菱形ABCD的面积=AE BC=BD×AC=OB AC,
∴AE===,
故选:A.
6.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积=BC AP=AB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP=,
∴AP=EF=,
∴EF的最小值为,
故选:C.
7.【解答】解:A、对角线互相垂直且相等的平行四边形是正方形,所以A选项错误.
B、当一组对边平行,另一组对边相等时,该四边形可能为等腰梯形,故B选项错误.
C、由一组对边平行,一组对角相等可得另一组对边平行,所以是平行四边形,故C选项正确.
D、对角线互相垂直的平行四边形是菱形,所以D选项错误;
故选:C.
8.选:B.
9.【解答】解:如图,过点B作BE⊥CM于E,
∵DN⊥CM,BE⊥CM,
∴∠DNC=∠CEB=90°,
∴∠DCN+∠CDN=90°,
∵四边形ABCD是正方形,
∴DC=CB,∠ABC=∠BCD=90°,
∴∠DCN+∠BCE=90°,
∴∠CDN=∠BCE,
∴△DCN≌△CBE(AAS),
∴DN=CE,CN=BE,
∵DN=2CN=2,
∴CN=BE=1,CE=2,
∴EN=CE﹣CN=2﹣1=1,
∴EN=BE=1,
∵∠BEN=90°,
∴△BNE是等腰直角三角形,
∴BN=BE=.
故选:B.
二、填空题
10.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=4,且点E为线段AD的中点,
∴AD=2OE=8.
∴C菱形ABCD=4AD=4×8=32.
故答案为:32.
11.【解答】解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE+∠EOF=∠COF+∠DOF=90°,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的 ,故③正确;
④在Rt△ECF中,∠EOF=90°,根据勾股定理,得:OE2+OF2=EF2,故④正确;
综上所述,正确的是①②③④,
故答案为:①②③④.
12.【解答】解:答案为:.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
16.【解答】(1)证明:∵AF∥BC,
∴∠AFC=∠FCD,∠FAE=∠CDE,
∵点E是AD的中点,
∴AE=DE,
∴△FAE≌△CDE(AAS),
∴AF=CD,
∵点D是BC的中点,
∴BD=CD,
∴AF=BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD=BC,
∴四边形ADBF是菱形;
(2)解:∵四边形ADBF是菱形,
∴菱形ADBF的面积=2△ABD的面积,
∵点D是BC的中点,
∴△ABC的面积=2△ABD的面积,
∴菱形ADBF的面积=△ABC的面积=40,
∴AB AC=40,
∴×8 AC=40,
∴AC=10,
∴AC的长为10.
17.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N,
∵四边形ABCD是正方形,
∴∠EAD=∠EAB=45°,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=90°﹣∠MEF=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=2,∠GDE=∠ADC=90°,
∴∠ADG=90°﹣∠ADE=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∵正方形ABCD中,AC=AB=2,
∴AC=AB=2,
∴AE+AG=AE+EC=AC=2.
18.【解答】(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD=,∠DAG=∠ADG=45°,
∴DF=﹣1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF=﹣1.
∴OF=﹣1.
19.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=AC=AB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG===3,
∴DE=EG=3.
∴正方形DEFG的边长为3.
20.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)解:△CPF是等腰三角形,理由如下:
∵△ADE≌△CDE,
∴∠DAE=∠DCE,
又∵CP⊥CE,DC⊥CF,
∴∠DCE=∠PCF,
又∵AD∥BF,
∴∠DAE=∠CFP,
∴∠PCF=∠PFC,
∴CP=PF,
∴△CPF是等腰三角形;
(3)解:如图,连接DF,
∵∠PCF=∠PFC,
∴∠PCM=∠PMC,
∴PC=MP,
∴MP=PF,
又∵点N是DM的中点,
∴DF=2NP=6,
∴CF===2.
21.【解答】(1)证明:如图,连接CE.
∵四边形ABCD是正方形,
∴点A,C关于BD对称,
∴CE=AE,∠DCE=∠DAE.
∵∠AEF+∠FDA=180°,
∴∠EFD+∠EAD=180°,
又∠EFC+∠DFE=180°,
∴∠DCE=∠CFE,
∴EC=FE,
∴AE=FE;
(2)由四边形ABCD是正方形,
得AD=AB=2,∠EBA=∠EDF=45°,.
由AD=ED,
得AB=DE,∠EAD=∠DEA,
得∠BAD﹣∠DAE=∠FEA﹣∠DEA,即∠BAE=∠DEF,
得△EBA≌△FDE,
得,
得.
22.【解答】(1)①证明:∵DP⊥DE,
∴∠PDE=∠PDC+∠CDE=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠ADP+∠PDC=90°,AD=CD,
∴∠CDE=∠ADP,
在△APD和△CED中,
,
∴△APD≌△CED(SAS);
②解:∵△APD≌△CED,
∴∠APD=∠CED,
∵∠APD=∠PDE+∠DEP,∠CED=∠CEA+∠DEP,
∴∠PDE+∠DEP=∠CEA+∠DEP,
∴∠AEC=∠PDE=90°;
(2)解:过点C作CF⊥DE交DE延长线于点F,则∠EFC=90°,
∵∠PDE=90°,DE=DP=1,
∴∠DPE=∠DEP=45°,,
∵∠CEA=90°,
∴∠CEF=45°,
∵∠EFC=90°,
∴∠FCE=45°,
∴∠CEF=∠FCE,
∴EF=CF,
∴,
设EF=CF=x,
∴EF2+CF2=CE2,
∴,
∴x=3,
∴CF=EF=3,
在Rt△CDF中,CD2=CF2+DF2=32+(1+3)2=25,
∴正方形ABCD的面积为:CD2=25.
23.【解答】(1)证明:∵四边形ABCD,AEFG均为正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∵∠BAE+∠EAD=90°,∠EAD+∠DAG=90°,
∴∠BAE=∠DAG,
在△BAE和△DAG中,
,
∴△BAE≌△DAG(SAS),
∴BE=DG;
(2)证明:∵△BAE≌△DAG,
∴∠GDA=∠ABE,
∵AB∥CD,
∴∠ABE=∠CEB,
∴∠CEB=∠GDA,
∵∠CEB=∠DEQ,
∴∠DEQ=∠GDA,
又∵∠ADC=90°,∠GDA+∠QDE=90°,
∴∠QDE+∠DEQ=90°,
∴∠Q=90°,
∴BE⊥GD;
(3)解:∵∠QED=60°,
∴∠CEB=60°,
又∵AB=BC=3,
∴,
∴,
∴,
∴.
24.【解答】(1)证明:∵四边形ABCD和CEFG都是正方形,
∴AB=AD=DC=BC,GC=EC=FG=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS),
∴AK=AH;
(2)证明:∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形;
(3)解:∵四边形AKFH的面积为10,
∴KF=,
∵EF=CE=1,
∴KE=,
∴AB=KE=3,
∵BK=EF=1,
∴BE=BK+KE=4,
∴AE=,
故点A,E之间的距离为5.
21世纪教育网(www.21cnjy.com)
18.2特殊平行四边形期中复习人教版2024—2025学年八年级下册
一、选择题
1.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=10,则CD=( )
A.10 B.6 C.8 D.5
2.如图, ABCD的对角线AC、BD相交于点O,添加一个条件,使得 ABCD是菱形,则下列选项不符合题意的是( )
A.AC=BD B.AC⊥BD C.AB=BC D.∠ABD=∠CBD
3.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
4.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
5.如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
6.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A.5 B.4 C. D.3
7.下列说法正确的是( )
A.对角线互相垂直的平行四边形是正方形
B.一组对边平行另一组对边相等的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线互相垂直的四边形是菱形
8.如图,在Rt△ABC中,∠ACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点Q,若HF=FG,则的值是( )
A. B. C. D.
9.如图,点M是正方形ABCD边AB上一点,DN⊥CM于N,DN=2CN=2,则BN的长度为( )
A.2 B. C. D.
二、填空题
10.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD中点,OE=4,则菱形ABCD的周长为 .
11.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:
(1)△DOF≌△COE;
(2)CF=BE;
(3)四边形CEOF的面积为正方形ABCD面积的;
(4)OF2+OE2=EF2.其中正确的是 .
12.如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形ABCD的周长为 cm.
三、解答题
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
15.如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
16.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
17.如图,正方形ABCD中,AB=2,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值.
18.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
19.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
20.如图,已知正方形ABCD,AB=4,点M在边CD上,射线AM交BD于点E,交射线BC于点F,过点C作CP⊥CE,交AF于点P.
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连结PN,若PN=3,求CF的长.
21.点E是正方形ABCD的对角线BD上一点,过点E作EF⊥AE交CD于点F,AE的延长线交BC于点G,AF交BD于点H.
(1)如图1,证明:AE=EF;
(2)如图2,若AD=DE,AB=2,求CF的长.
22.如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,交边AB于点Q,.
(1)①求证:△APD≌△CED;②求∠AEC的大小;
(2)求正方形ABCD的面积.
23.已知正方形ABCD中,AB=3,且E为CD上的一动点,以AE为边作正方形AGFE,如图1所示,连接BE、GD.
(1)求证:BE=GD.
(2)如图2,延长GD、BE交于点Q,求证:BE⊥GD.
(3)若∠QED=60°,则DE的值是多少?
24.如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH;
(2)求证:四边形AKFH是正方形;
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
参考答案
一、选择题
1.【解答】解:∵在Rt△ABC中,CD是斜边AB上的中线,且AB=10,
∴,
故选:D.
2.【解答】解:∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,但四边形ABCD不一定是菱形,
故A选项不符合题意;
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
故B选项符合题意;
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
故C选项符合题意;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴四边形ABCD是菱形,
故D选项符合题意,
故选:A.
3.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不符合题意;
B、是对角线相等,可推出平行四边形ABCD是矩形,故符合题意;
C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不符合题意;
D、无法判断.
故选:B.
4.【解答】解:A、对角线AC与BD互相垂直,AC=BD时,无法得出四边形ABCD是矩形,故此选项不合题意;
B、当AB=AD,CB=CD时,无法得到,四边形ABCD是菱形,故此选项不合题意;
C、当两条对角线AC与BD互相垂直,AB=AD=BC时,∴BO=DO,AO=CO,
∴四边形ABCD是平行四边形,
∵两条对角线AC与BD互相垂直,
∴平行四边形ABCD是菱形,故此选项正确;
D、当AC=BD,AD=AB时,无法得到四边形ABCD是正方形,故此选项不合题意;
故选:C.
5.【解答】解:∵四边形ABCD是菱形,CD=5,BD=8,
∴BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,
∴∠BOC=90°,
在Rt△OBC中,由勾股定理得:OC===3,
∴AC=2OC=6,
∵菱形ABCD的面积=AE BC=BD×AC=OB AC,
∴AE===,
故选:A.
6.【解答】解:连接AP,
∵AB=6,AC=8,BC=10,
∴AB2+AC2=62+82=100,BC2=102=100,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∴当AP⊥BC时,AP有最小值,即EF有最小值,
∵△ABC的面积=BC AP=AB AC,
∴BC AP=AB AC,
∴10AP=6×8,
∴AP=,
∴AP=EF=,
∴EF的最小值为,
故选:C.
7.【解答】解:A、对角线互相垂直且相等的平行四边形是正方形,所以A选项错误.
B、当一组对边平行,另一组对边相等时,该四边形可能为等腰梯形,故B选项错误.
C、由一组对边平行,一组对角相等可得另一组对边平行,所以是平行四边形,故C选项正确.
D、对角线互相垂直的平行四边形是菱形,所以D选项错误;
故选:C.
8.选:B.
9.【解答】解:如图,过点B作BE⊥CM于E,
∵DN⊥CM,BE⊥CM,
∴∠DNC=∠CEB=90°,
∴∠DCN+∠CDN=90°,
∵四边形ABCD是正方形,
∴DC=CB,∠ABC=∠BCD=90°,
∴∠DCN+∠BCE=90°,
∴∠CDN=∠BCE,
∴△DCN≌△CBE(AAS),
∴DN=CE,CN=BE,
∵DN=2CN=2,
∴CN=BE=1,CE=2,
∴EN=CE﹣CN=2﹣1=1,
∴EN=BE=1,
∵∠BEN=90°,
∴△BNE是等腰直角三角形,
∴BN=BE=.
故选:B.
二、填空题
10.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=4,且点E为线段AD的中点,
∴AD=2OE=8.
∴C菱形ABCD=4AD=4×8=32.
故答案为:32.
11.【解答】解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE+∠EOF=∠COF+∠DOF=90°,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的 ,故③正确;
④在Rt△ECF中,∠EOF=90°,根据勾股定理,得:OE2+OF2=EF2,故④正确;
综上所述,正确的是①②③④,
故答案为:①②③④.
12.【解答】解:答案为:.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
16.【解答】(1)证明:∵AF∥BC,
∴∠AFC=∠FCD,∠FAE=∠CDE,
∵点E是AD的中点,
∴AE=DE,
∴△FAE≌△CDE(AAS),
∴AF=CD,
∵点D是BC的中点,
∴BD=CD,
∴AF=BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD=BC,
∴四边形ADBF是菱形;
(2)解:∵四边形ADBF是菱形,
∴菱形ADBF的面积=2△ABD的面积,
∵点D是BC的中点,
∴△ABC的面积=2△ABD的面积,
∴菱形ADBF的面积=△ABC的面积=40,
∴AB AC=40,
∴×8 AC=40,
∴AC=10,
∴AC的长为10.
17.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N,
∵四边形ABCD是正方形,
∴∠EAD=∠EAB=45°,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=90°﹣∠MEF=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=2,∠GDE=∠ADC=90°,
∴∠ADG=90°﹣∠ADE=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∵正方形ABCD中,AC=AB=2,
∴AC=AB=2,
∴AE+AG=AE+EC=AC=2.
18.【解答】(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD=,∠DAG=∠ADG=45°,
∴DF=﹣1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF=﹣1.
∴OF=﹣1.
19.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=AC=AB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG===3,
∴DE=EG=3.
∴正方形DEFG的边长为3.
20.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)解:△CPF是等腰三角形,理由如下:
∵△ADE≌△CDE,
∴∠DAE=∠DCE,
又∵CP⊥CE,DC⊥CF,
∴∠DCE=∠PCF,
又∵AD∥BF,
∴∠DAE=∠CFP,
∴∠PCF=∠PFC,
∴CP=PF,
∴△CPF是等腰三角形;
(3)解:如图,连接DF,
∵∠PCF=∠PFC,
∴∠PCM=∠PMC,
∴PC=MP,
∴MP=PF,
又∵点N是DM的中点,
∴DF=2NP=6,
∴CF===2.
21.【解答】(1)证明:如图,连接CE.
∵四边形ABCD是正方形,
∴点A,C关于BD对称,
∴CE=AE,∠DCE=∠DAE.
∵∠AEF+∠FDA=180°,
∴∠EFD+∠EAD=180°,
又∠EFC+∠DFE=180°,
∴∠DCE=∠CFE,
∴EC=FE,
∴AE=FE;
(2)由四边形ABCD是正方形,
得AD=AB=2,∠EBA=∠EDF=45°,.
由AD=ED,
得AB=DE,∠EAD=∠DEA,
得∠BAD﹣∠DAE=∠FEA﹣∠DEA,即∠BAE=∠DEF,
得△EBA≌△FDE,
得,
得.
22.【解答】(1)①证明:∵DP⊥DE,
∴∠PDE=∠PDC+∠CDE=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠ADP+∠PDC=90°,AD=CD,
∴∠CDE=∠ADP,
在△APD和△CED中,
,
∴△APD≌△CED(SAS);
②解:∵△APD≌△CED,
∴∠APD=∠CED,
∵∠APD=∠PDE+∠DEP,∠CED=∠CEA+∠DEP,
∴∠PDE+∠DEP=∠CEA+∠DEP,
∴∠AEC=∠PDE=90°;
(2)解:过点C作CF⊥DE交DE延长线于点F,则∠EFC=90°,
∵∠PDE=90°,DE=DP=1,
∴∠DPE=∠DEP=45°,,
∵∠CEA=90°,
∴∠CEF=45°,
∵∠EFC=90°,
∴∠FCE=45°,
∴∠CEF=∠FCE,
∴EF=CF,
∴,
设EF=CF=x,
∴EF2+CF2=CE2,
∴,
∴x=3,
∴CF=EF=3,
在Rt△CDF中,CD2=CF2+DF2=32+(1+3)2=25,
∴正方形ABCD的面积为:CD2=25.
23.【解答】(1)证明:∵四边形ABCD,AEFG均为正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∵∠BAE+∠EAD=90°,∠EAD+∠DAG=90°,
∴∠BAE=∠DAG,
在△BAE和△DAG中,
,
∴△BAE≌△DAG(SAS),
∴BE=DG;
(2)证明:∵△BAE≌△DAG,
∴∠GDA=∠ABE,
∵AB∥CD,
∴∠ABE=∠CEB,
∴∠CEB=∠GDA,
∵∠CEB=∠DEQ,
∴∠DEQ=∠GDA,
又∵∠ADC=90°,∠GDA+∠QDE=90°,
∴∠QDE+∠DEQ=90°,
∴∠Q=90°,
∴BE⊥GD;
(3)解:∵∠QED=60°,
∴∠CEB=60°,
又∵AB=BC=3,
∴,
∴,
∴,
∴.
24.【解答】(1)证明:∵四边形ABCD和CEFG都是正方形,
∴AB=AD=DC=BC,GC=EC=FG=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS),
∴AK=AH;
(2)证明:∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形;
(3)解:∵四边形AKFH的面积为10,
∴KF=,
∵EF=CE=1,
∴KE=,
∴AB=KE=3,
∵BK=EF=1,
∴BE=BK+KE=4,
∴AE=,
故点A,E之间的距离为5.
21世纪教育网(www.21cnjy.com)
同课章节目录
