人教版2024—2025学年八年级下册数学期中考试模拟试卷(含解析)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期中考试模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 643.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 17:45:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.以下列各组数为边长,能构成直角三角形的是( )
A.4、8、12 B.6、8、10 C.4、6、8 D.4、5、6
2.若在实数范围内有意义,则x的取值范围是( )
A.x<2024 B.x≤2024 C.x>2024 D.x≥2024
3.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )
A. B.13 C. D.
4.给出下列判断,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.有一条对角线平分一个内角的平行四边形为菱形
D.一组对边平行,另一组对边相等的四边形是平行四边形
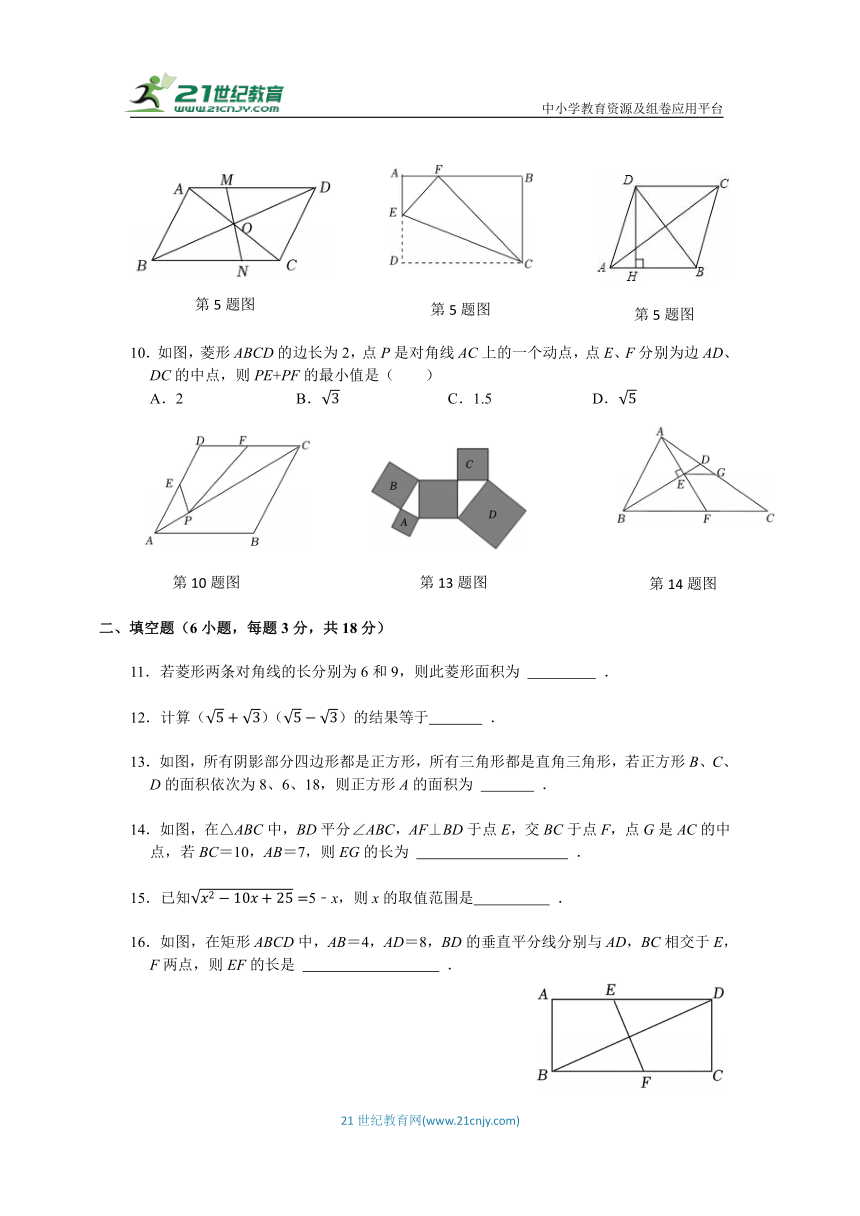
5.如图, ABCD中,点O是对角线AC,BD的交点,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则 ABCD的面积是( )
A.12 B.16 C.24 D.32
6.如图,在矩形ABCD纸片中,E为AD上一点,将△CDE沿CE翻折至△CFE.若点F恰好落在AB上,AB=10,BC=6,则EF=( )
A. B. C.2 D.
7.已知,则2xy的值为( )
A.﹣15 B.15 C. D.
8.若三角形的三边长分别为a、b、c,且满足(a﹣3)2+|b﹣4|0,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
9.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
10.如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE+PF的最小值是( )
A.2 B. C.1.5 D.
二、填空题(6小题,每题3分,共18分)
11.若菱形两条对角线的长分别为6和9,则此菱形面积为 .
12.计算()()的结果等于 .
13.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为8、6、18,则正方形A的面积为 .
14.如图,在△ABC中,BD平分∠ABC,AF⊥BD于点E,交BC于点F,点G是AC的中点,若BC=10,AB=7,则EG的长为 .
15.已知5﹣x,则x的取值范围是 .
16.如图,在矩形ABCD中,AB=4,AD=8,BD的垂直平分线分别与AD,BC相交于E,F两点,则EF的长是 .
第II卷
人教版2024—2025学年八年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1)﹣4; (2).
18.已知,.
(1)求a+b和ab的值;
(2)求a2+b2﹣3ab的值.
19.为了强化实践育人,有效开展劳动教育和综合实践活动,我市某中学现有一块四边形的空地ABCD,如图所示,学校决定开发该空地作为学生劳动实践基地.经学校课外实践活动小组测量得到:∠BAD=90°,AD=3m,AB=4m,BC=13m,CD=12m.根据你所学过的知识,解决下列问题:
(1)四边形ABCD的面积;
(2)点D到BC的距离.
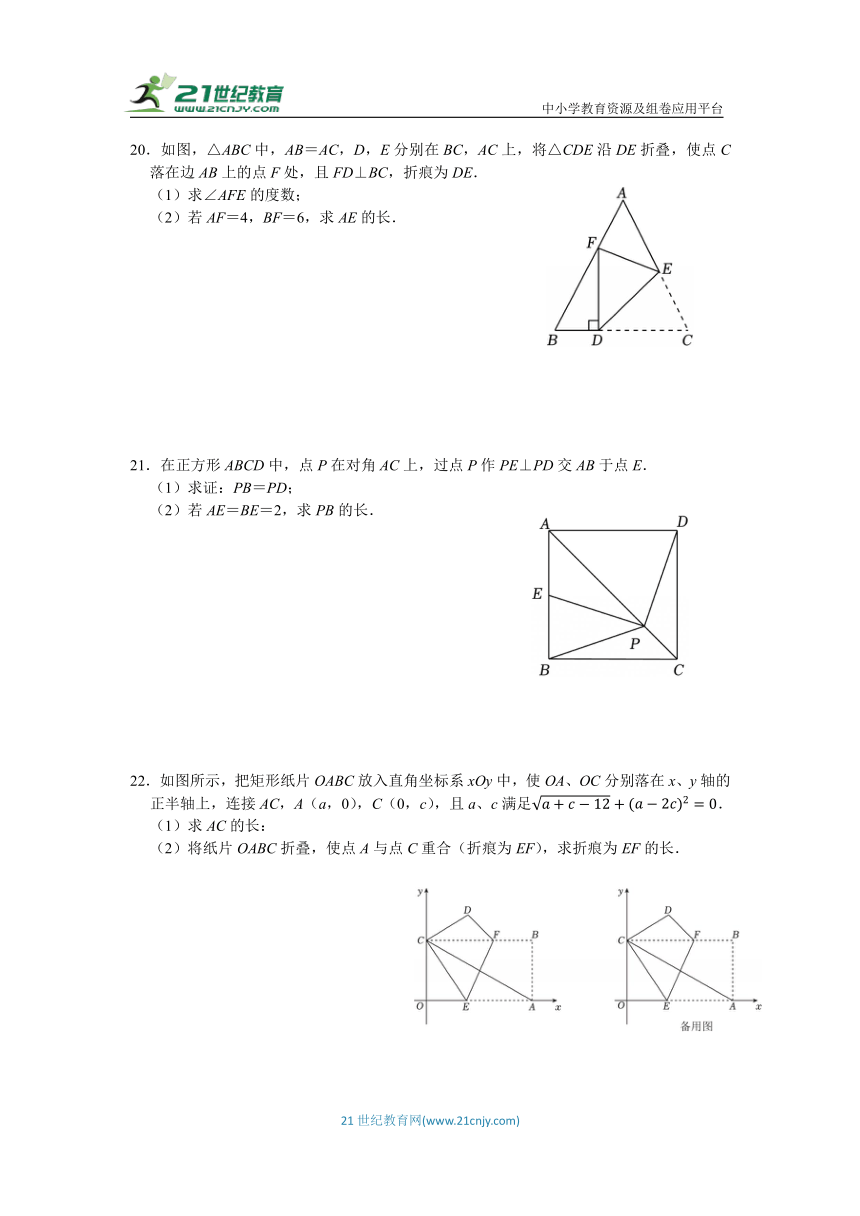
20.如图,△ABC中,AB=AC,D,E分别在BC,AC上,将△CDE沿DE折叠,使点C落在边AB上的点F处,且FD⊥BC,折痕为DE.
(1)求∠AFE的度数;
(2)若AF=4,BF=6,求AE的长.
21.在正方形ABCD中,点P在对角AC上,过点P作PE⊥PD交AB于点E.
(1)求证:PB=PD;
(2)若AE=BE=2,求PB的长.
22.如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,A(a,0),C(0,c),且a、c满足.
(1)求AC的长:
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折痕为EF的长.
23.任意一个无理数介于两个整数之间,我们定义,若无理数T:m<T<n,(其中m、n为连续的整数),则称无理数的“美好区间”为(m,n),如,所以的“美好区间”为(1,2).
(1)无理数的“美好区间”是 ;
(2)若一个无理数的“美好区间”为(m,n),且满足,其中是关于x,y的二元一次方程mx﹣ny=C的一组正整数解,求C的值.
(3)实数x,y,m满足如下关系式:(2x+3y+m)2+(3x+2y﹣3m)2,求m的算术平方根的“美好区间”.
24.若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.
(1)下列三组数是“快乐三数组”有 (填序号):
①3,4,7
②,,
③,1,
(2)若,,1(m≠0)构成“快乐三数组”,求m的值.
(3)如图,在四边形ADBC中,∠C=∠D=90°,BD=AD,连接对角线AB,若AB的长为c,∠C的两条邻边长分别为a,b,若c﹣a,b,c+a构成“快乐三数组”,且S△ABD﹣S△ABC=6,求AB的长.
25.如图,在平面直角坐标系中,菱形ABCD的顶点A,B的坐标分别是(0,8),(﹣6,0),顶点C在x轴上,顶点D在第一象限,对角线BD交AC于点E,交y轴于点F.
(1)求C,D两点的坐标;
(2)求EF的长;
(3)是否存在以P,B,E,C为顶点的四边形是矩形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1.【解答】解:A、因为42+82≠22,所以不能构成直角三角形;
B、因为62+82=102,所以能构成直角三角形;
C、因为42+62≠82,所以不能构成直角三角形;
D、因为42+52≠62,所以不能构成直角三角形.
故选:B.
2.【解答】解:由题意可知:x﹣2024≥0,
解得x≥2024.
故选:D.
3.【解答】解:∵直角三角形的两条直角边的长分别为5,12,
∴斜边为13.
设h为斜边上的高.
∵S△ABC5×1213h,
∴h.
故选:D.
4.【解答】解:A、对角线相等的平行四边形是矩形,故不符合题意;
B、对角线互相垂直且相等的平行四边形是正方形,故不符合题意;
C、有一条对角线平分一个内角的平行四边形为菱形,故符合题意;
D、一组对边平行,另一组对边相等的四边形不一定是平行四边形,故不符合题意;
故选:C.
5.【解答】解:∵四边形ABCD是平行四边形,点O是对角线AC,BD的交点,
∴四边形ABCD是中心对称图形,OB=OD,
∴S△CON=S△AOM,S△ABD=S△CBD,
∵S△AOD=S△AOM+S△DOM=2+4=6,
∴S△AOB=S△AOD=6,
∴S△ABD=S△AOB+S△AOD=12,
∴S ABCD=2S△ABD=24,
故选:C.
6.【解答】解:∵四边形ABCD是矩形,
∴CD=AB=10,AD=BC=6,∠A=∠B=90°,
由折叠的性质可得:CF=CD=AB=10,DE=EF,
∴,
∴AF=AB﹣BF=2,
设EF=x,则AE=AD﹣DE=6﹣x,
由勾股定理得:AE2+AF2=EF2,
∴(6﹣x)2+22=x2,
解得:,
∴,
故选:A.
7.【解答】解:要使有意义,则,
解得x,
故y=﹣3,
∴2xy=2(﹣3)=﹣15.
故选:A.
8.【解答】解:∵(a﹣3)2+|b﹣4|0,
∴a﹣3=0,b﹣4=0,c﹣5=0,
∴a=3,b=4,c=5,
∵32+42=52=25,
∴这个三角形是直角三角形.
故选:B.
9.【解答】解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB5,
∵S菱形ABCD,
∴,
∴DH,
故选:A.
10.【解答】解:如图,取AB的中点T,连接PT,FT.
∵四边形ABCD是菱形,
∴CD∥AB,CD=AB,
∵DF=CF,AT=TB,
∴DF=AT,DF∥AT,
∴四边形ADFT是平行四边形,
∴AD=FT=2,
∵四边形ABCD是菱形,AE=DE,AT=TB,
∴E,T关于AC对称,
∴PE=PT,
∴PE+PF=PT+PF,
∵PF+PT≥FT=2,
∴PE+PF≥2,
∴PE+PF的最小值为2.
故选:A.
二、填空题
11.【解答】解:菱形的面积为:.
故答案为:27.
12.【解答】解:原式=()2﹣()2
=5﹣3
=2,
故答案为:2.
13.【解答】解:由勾股定理,得正方形E的面积=正方形D的面积﹣正方形C的面积,正方形E的面积=正方形A的面积+正方形B的面积,
则正方形A的面积=18﹣6﹣8=4,
故答案为:4.
14.【解答】解:∵BD平分∠ABC,AF⊥BD,
∴∠ABE=∠FBE,∠AEB=∠FEB=90°,
∵BE=BE,
∴△ABE≌△FBE(ASA),
∴BF=AB=7,AE=EF,
∵BC=10,
∴CF=3,
∵点G是AC的中点,
∴AG=CG,
∴EG是△AFC的中位线,
∴EGCF,
故选:.
15.【解答】解:∵5﹣x,
∴5﹣x≥0,
解得:x≤5.
故答案为:x≤5.
16.【解答】解:如图,连接BE,DF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
∵EF垂直平分BD,
∴EF⊥BD,BO=DO,
在△BFO和△DEO中,
,
∴△BFO≌△DEO(AAS),
∴BF=DE,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
∴BF=BE=ED,
在Rt△ABE中,AB2+AE2=BE2,
∴42+(8﹣BE)2=BE2,
解得BE=5,
∴DE=5,
∵AB=4,AD=8,
∴BD4,
∴S菱形EBFD=DE ABEF BD,
∴5×44EF,
∴EF=2,
故答案为:.
三、解答题
17.【解答】解:(1)
;
(2)
=0.
18.【解答】解:(1)∵,,
∴,;
(2)由(1)得:a+b=6,ab=4,
∴a2+b2﹣3ab=(a+b)2﹣5ab=62﹣5×4=16.
19.【解答】解:(1)如图1,连接BD,
∵∠BAD=90°,AD=3m,AB=4m,
∴BD5(m),
∵52+122=132,
∴BD2+CD2=BC2,
∴△BDC是直角三角形,且∠BDC=90°,
∴S四边形ABCD=SRt△ABD+SRt△BDCAB ADBD CD(4×3+5×12)=36(m2),
答:四边形土地的面积为36m2;
(2)如图2,过点D作DE⊥BC于点E,
由(1)可知,△BDC是直角三角形,∠BDC=90°,
∴S△BDCBC DEBD CD,
∴DE(m),
答:点D到BC的距离为m.
20.【解答】解:(1)∵AB=AC
∴∠B=∠C,
∵折叠等腰三角形纸片ABC,使点C落在边AB上的点F处,
∴∠EFD=∠C,
∴∠B=∠EFD,
∴180°﹣∠B=180°﹣∠EFD,即∠BDF+∠BFD=∠AFE+∠BFD,
∴∠BDF=∠AFE,
∵FD⊥BC,
∴∠BDF=90°,
∴∠AFE=90°;
(2)∵AF=4,BF=6,
∴AB=AF+BF=10=AC,
设AE=x,则CE=10﹣x,
∵折叠等腰三角形纸片ABC,使点C落在边AB上的点F处,
∴EF=CE=10﹣x,
在Rt△AFE中,AF2+EF2=AE2,
∴42+(10﹣x)2=x2,
解得,
∴.
21.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAC=∠DAC,
∵AP=AP,
∴△PAB≌△PAD(SAS),
∴PB=PD;
(2)解:连接DE,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵PE⊥PD,
∴∠DPE=90°,
∴PE2+PD2=DE2=AE2+AD2=20,
∵∠DPE+∠BAD+∠PEA+∠PDA=360°,
∴∠PEA+∠PDA=180°.
∵∠PEA+∠PEB=180°,
∴∠PEB=∠PDA.
∵△PAB≌△PAD,
∴∠PBA=∠PDA.
∴∠PBA=∠PEB.
∴PE=PB.
∵PB=PD,
∴PE=PD.
∴PD2=10.
∴PB=PD.
22.【解答】解:(1)∵,
∴,
解得:,
∴OA=8,OC=4,
在Rt△AOC中,;
(2)由翻折得EA=EC,AC⊥EH,AH=HC,设EA=EC=x,则OE=8﹣x,
在Rt△COE中,由勾股定理得:x2=42+(8﹣x)2,
解得:x=5,
∵,
∴,
解得:,
∵四边形ABCO是矩形,
∴BC∥OA,
∴∠CFH=∠AEH,
∵∠CHF=∠AHE,AH=HC,
∴△CHF≌△AHE,
∴EH=HF,
∴.
23.【解答】解:(1)∵,
∴,
∴,
∴无理数的“美好区间”是(﹣4,﹣3),
故答案为:(﹣4,﹣3);
(2)∵m、n为连续的整数,是关于x,y的二元一次方程mx﹣ny=C的一组正整数解,
∴是正整数,m>0,
∵,
∴满足题意的m,n的值为:或,
∴或,
当时,C=8×8﹣9×3=64﹣27=37;
当或时,C=15×15﹣16×4=225﹣64=161,
综上可知:C的值为:37或161;
(3)∵(2x+3y+m)2+(3x+2y﹣3m)2,x+y﹣2024≥0,2024﹣x﹣y≥0,
∴x+y﹣2024=2024﹣x﹣y=0,
∴x+y=2024,
∵(2x+3y+m)2+(3x+2y﹣3m)2,
∴(2x+3y+m)2+(3x+2y﹣3m)2=0,
∵(2x+3y+m)2≥0,(3x+2y﹣3m)2≥0,
∴2x+3y+m=0①,3x+2y﹣3m=0②,
①+②得:5x+5y﹣2m=0,
5(x+y)﹣2m=0,
5×2024﹣2m=0,
解得:m=5060,
∴,
即,
∴m的算术平方根的“美好区间”为(71,72).
24.【解答】解:(1)①∵若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.,
∴3,4,7不是“快乐三数组”;
②∵,
∴,,是“快乐三数组”;
③∵,
∴,1,是“快乐三数组”,
故答案为:②③.
(2)若,,1(m≠0)构成“快乐三数组”,则:
,,
①当时,
解得,经检验是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
②时,
解得m=﹣2,经检验m=﹣2是该方程的根,此时,不是正数,不构成“快乐三数组”;
③时,
解得m=1,经检验m=1是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
综上所述:m=1或.
(3)∵∠C=∠D=90°,若AB的长为c,∠C的两条邻边长分别为a,b,
∴a2+b2=c2,且0<c﹣a<b<c+a
∴,
∵c﹣a,b,c+a构成“快乐三数组”,
∴,
∴
,
将a2+b2=c2代入上式,得:,
∴b=2a,
∴,
在Rt△ABD中,BD=AD,
由勾股定理得:AD2+BD2=AB2,
∴,
∴,
∵S△ABD﹣S△ABC=6,
∴,
解得或(不合题意,舍去),
∴AB=a=2.
25.【解答】解:(1)∵A(0,8),B(﹣6,0),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB,
∵四边形ABCD是菱形,
∴BC=AD=AB=10,AD∥BC,
∴OC=BC﹣OB=4,∠OAD=∠AOB=90°.
∴C(4,0),D(10,8).
(2)连接CF,
∵四边形ABCD是菱形,
∴AE=CE,BD⊥AC,
∴AF=CF,
∵∠AOC=90°,
∴AC,CE,
在Rt△OCF中,OF2+OC2=CF2,即(8﹣CF)2+42=CF2,
解得CF=5.
∴EF.
(3)存在.
∵BD⊥AC,
∴如图,当PB∥AC,PC∥BD时,四边形BECP的矩形,
取OA中点G,连接EG.
则OGOA=4,EGOC=2.
∴E(2,4),
由平移可知,将线段EC先向左平移8个单位再向下平移4个单位与线段BP重合(点C与点P重合),
∴P(﹣4,﹣4).
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.以下列各组数为边长,能构成直角三角形的是( )
A.4、8、12 B.6、8、10 C.4、6、8 D.4、5、6
2.若在实数范围内有意义,则x的取值范围是( )
A.x<2024 B.x≤2024 C.x>2024 D.x≥2024
3.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )
A. B.13 C. D.
4.给出下列判断,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直且相等的四边形是正方形
C.有一条对角线平分一个内角的平行四边形为菱形
D.一组对边平行,另一组对边相等的四边形是平行四边形
5.如图, ABCD中,点O是对角线AC,BD的交点,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则 ABCD的面积是( )
A.12 B.16 C.24 D.32
6.如图,在矩形ABCD纸片中,E为AD上一点,将△CDE沿CE翻折至△CFE.若点F恰好落在AB上,AB=10,BC=6,则EF=( )
A. B. C.2 D.
7.已知,则2xy的值为( )
A.﹣15 B.15 C. D.
8.若三角形的三边长分别为a、b、c,且满足(a﹣3)2+|b﹣4|0,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
9.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
10.如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE+PF的最小值是( )
A.2 B. C.1.5 D.
二、填空题(6小题,每题3分,共18分)
11.若菱形两条对角线的长分别为6和9,则此菱形面积为 .
12.计算()()的结果等于 .
13.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为8、6、18,则正方形A的面积为 .
14.如图,在△ABC中,BD平分∠ABC,AF⊥BD于点E,交BC于点F,点G是AC的中点,若BC=10,AB=7,则EG的长为 .
15.已知5﹣x,则x的取值范围是 .
16.如图,在矩形ABCD中,AB=4,AD=8,BD的垂直平分线分别与AD,BC相交于E,F两点,则EF的长是 .
第II卷
人教版2024—2025学年八年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1)﹣4; (2).
18.已知,.
(1)求a+b和ab的值;
(2)求a2+b2﹣3ab的值.
19.为了强化实践育人,有效开展劳动教育和综合实践活动,我市某中学现有一块四边形的空地ABCD,如图所示,学校决定开发该空地作为学生劳动实践基地.经学校课外实践活动小组测量得到:∠BAD=90°,AD=3m,AB=4m,BC=13m,CD=12m.根据你所学过的知识,解决下列问题:
(1)四边形ABCD的面积;
(2)点D到BC的距离.
20.如图,△ABC中,AB=AC,D,E分别在BC,AC上,将△CDE沿DE折叠,使点C落在边AB上的点F处,且FD⊥BC,折痕为DE.
(1)求∠AFE的度数;
(2)若AF=4,BF=6,求AE的长.
21.在正方形ABCD中,点P在对角AC上,过点P作PE⊥PD交AB于点E.
(1)求证:PB=PD;
(2)若AE=BE=2,求PB的长.
22.如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,A(a,0),C(0,c),且a、c满足.
(1)求AC的长:
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折痕为EF的长.
23.任意一个无理数介于两个整数之间,我们定义,若无理数T:m<T<n,(其中m、n为连续的整数),则称无理数的“美好区间”为(m,n),如,所以的“美好区间”为(1,2).
(1)无理数的“美好区间”是 ;
(2)若一个无理数的“美好区间”为(m,n),且满足,其中是关于x,y的二元一次方程mx﹣ny=C的一组正整数解,求C的值.
(3)实数x,y,m满足如下关系式:(2x+3y+m)2+(3x+2y﹣3m)2,求m的算术平方根的“美好区间”.
24.若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.
(1)下列三组数是“快乐三数组”有 (填序号):
①3,4,7
②,,
③,1,
(2)若,,1(m≠0)构成“快乐三数组”,求m的值.
(3)如图,在四边形ADBC中,∠C=∠D=90°,BD=AD,连接对角线AB,若AB的长为c,∠C的两条邻边长分别为a,b,若c﹣a,b,c+a构成“快乐三数组”,且S△ABD﹣S△ABC=6,求AB的长.
25.如图,在平面直角坐标系中,菱形ABCD的顶点A,B的坐标分别是(0,8),(﹣6,0),顶点C在x轴上,顶点D在第一象限,对角线BD交AC于点E,交y轴于点F.
(1)求C,D两点的坐标;
(2)求EF的长;
(3)是否存在以P,B,E,C为顶点的四边形是矩形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1.【解答】解:A、因为42+82≠22,所以不能构成直角三角形;
B、因为62+82=102,所以能构成直角三角形;
C、因为42+62≠82,所以不能构成直角三角形;
D、因为42+52≠62,所以不能构成直角三角形.
故选:B.
2.【解答】解:由题意可知:x﹣2024≥0,
解得x≥2024.
故选:D.
3.【解答】解:∵直角三角形的两条直角边的长分别为5,12,
∴斜边为13.
设h为斜边上的高.
∵S△ABC5×1213h,
∴h.
故选:D.
4.【解答】解:A、对角线相等的平行四边形是矩形,故不符合题意;
B、对角线互相垂直且相等的平行四边形是正方形,故不符合题意;
C、有一条对角线平分一个内角的平行四边形为菱形,故符合题意;
D、一组对边平行,另一组对边相等的四边形不一定是平行四边形,故不符合题意;
故选:C.
5.【解答】解:∵四边形ABCD是平行四边形,点O是对角线AC,BD的交点,
∴四边形ABCD是中心对称图形,OB=OD,
∴S△CON=S△AOM,S△ABD=S△CBD,
∵S△AOD=S△AOM+S△DOM=2+4=6,
∴S△AOB=S△AOD=6,
∴S△ABD=S△AOB+S△AOD=12,
∴S ABCD=2S△ABD=24,
故选:C.
6.【解答】解:∵四边形ABCD是矩形,
∴CD=AB=10,AD=BC=6,∠A=∠B=90°,
由折叠的性质可得:CF=CD=AB=10,DE=EF,
∴,
∴AF=AB﹣BF=2,
设EF=x,则AE=AD﹣DE=6﹣x,
由勾股定理得:AE2+AF2=EF2,
∴(6﹣x)2+22=x2,
解得:,
∴,
故选:A.
7.【解答】解:要使有意义,则,
解得x,
故y=﹣3,
∴2xy=2(﹣3)=﹣15.
故选:A.
8.【解答】解:∵(a﹣3)2+|b﹣4|0,
∴a﹣3=0,b﹣4=0,c﹣5=0,
∴a=3,b=4,c=5,
∵32+42=52=25,
∴这个三角形是直角三角形.
故选:B.
9.【解答】解:设AC交BD于O,
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB5,
∵S菱形ABCD,
∴,
∴DH,
故选:A.
10.【解答】解:如图,取AB的中点T,连接PT,FT.
∵四边形ABCD是菱形,
∴CD∥AB,CD=AB,
∵DF=CF,AT=TB,
∴DF=AT,DF∥AT,
∴四边形ADFT是平行四边形,
∴AD=FT=2,
∵四边形ABCD是菱形,AE=DE,AT=TB,
∴E,T关于AC对称,
∴PE=PT,
∴PE+PF=PT+PF,
∵PF+PT≥FT=2,
∴PE+PF≥2,
∴PE+PF的最小值为2.
故选:A.
二、填空题
11.【解答】解:菱形的面积为:.
故答案为:27.
12.【解答】解:原式=()2﹣()2
=5﹣3
=2,
故答案为:2.
13.【解答】解:由勾股定理,得正方形E的面积=正方形D的面积﹣正方形C的面积,正方形E的面积=正方形A的面积+正方形B的面积,
则正方形A的面积=18﹣6﹣8=4,
故答案为:4.
14.【解答】解:∵BD平分∠ABC,AF⊥BD,
∴∠ABE=∠FBE,∠AEB=∠FEB=90°,
∵BE=BE,
∴△ABE≌△FBE(ASA),
∴BF=AB=7,AE=EF,
∵BC=10,
∴CF=3,
∵点G是AC的中点,
∴AG=CG,
∴EG是△AFC的中位线,
∴EGCF,
故选:.
15.【解答】解:∵5﹣x,
∴5﹣x≥0,
解得:x≤5.
故答案为:x≤5.
16.【解答】解:如图,连接BE,DF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
∵EF垂直平分BD,
∴EF⊥BD,BO=DO,
在△BFO和△DEO中,
,
∴△BFO≌△DEO(AAS),
∴BF=DE,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
∴BF=BE=ED,
在Rt△ABE中,AB2+AE2=BE2,
∴42+(8﹣BE)2=BE2,
解得BE=5,
∴DE=5,
∵AB=4,AD=8,
∴BD4,
∴S菱形EBFD=DE ABEF BD,
∴5×44EF,
∴EF=2,
故答案为:.
三、解答题
17.【解答】解:(1)
;
(2)
=0.
18.【解答】解:(1)∵,,
∴,;
(2)由(1)得:a+b=6,ab=4,
∴a2+b2﹣3ab=(a+b)2﹣5ab=62﹣5×4=16.
19.【解答】解:(1)如图1,连接BD,
∵∠BAD=90°,AD=3m,AB=4m,
∴BD5(m),
∵52+122=132,
∴BD2+CD2=BC2,
∴△BDC是直角三角形,且∠BDC=90°,
∴S四边形ABCD=SRt△ABD+SRt△BDCAB ADBD CD(4×3+5×12)=36(m2),
答:四边形土地的面积为36m2;
(2)如图2,过点D作DE⊥BC于点E,
由(1)可知,△BDC是直角三角形,∠BDC=90°,
∴S△BDCBC DEBD CD,
∴DE(m),
答:点D到BC的距离为m.
20.【解答】解:(1)∵AB=AC
∴∠B=∠C,
∵折叠等腰三角形纸片ABC,使点C落在边AB上的点F处,
∴∠EFD=∠C,
∴∠B=∠EFD,
∴180°﹣∠B=180°﹣∠EFD,即∠BDF+∠BFD=∠AFE+∠BFD,
∴∠BDF=∠AFE,
∵FD⊥BC,
∴∠BDF=90°,
∴∠AFE=90°;
(2)∵AF=4,BF=6,
∴AB=AF+BF=10=AC,
设AE=x,则CE=10﹣x,
∵折叠等腰三角形纸片ABC,使点C落在边AB上的点F处,
∴EF=CE=10﹣x,
在Rt△AFE中,AF2+EF2=AE2,
∴42+(10﹣x)2=x2,
解得,
∴.
21.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAC=∠DAC,
∵AP=AP,
∴△PAB≌△PAD(SAS),
∴PB=PD;
(2)解:连接DE,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵PE⊥PD,
∴∠DPE=90°,
∴PE2+PD2=DE2=AE2+AD2=20,
∵∠DPE+∠BAD+∠PEA+∠PDA=360°,
∴∠PEA+∠PDA=180°.
∵∠PEA+∠PEB=180°,
∴∠PEB=∠PDA.
∵△PAB≌△PAD,
∴∠PBA=∠PDA.
∴∠PBA=∠PEB.
∴PE=PB.
∵PB=PD,
∴PE=PD.
∴PD2=10.
∴PB=PD.
22.【解答】解:(1)∵,
∴,
解得:,
∴OA=8,OC=4,
在Rt△AOC中,;
(2)由翻折得EA=EC,AC⊥EH,AH=HC,设EA=EC=x,则OE=8﹣x,
在Rt△COE中,由勾股定理得:x2=42+(8﹣x)2,
解得:x=5,
∵,
∴,
解得:,
∵四边形ABCO是矩形,
∴BC∥OA,
∴∠CFH=∠AEH,
∵∠CHF=∠AHE,AH=HC,
∴△CHF≌△AHE,
∴EH=HF,
∴.
23.【解答】解:(1)∵,
∴,
∴,
∴无理数的“美好区间”是(﹣4,﹣3),
故答案为:(﹣4,﹣3);
(2)∵m、n为连续的整数,是关于x,y的二元一次方程mx﹣ny=C的一组正整数解,
∴是正整数,m>0,
∵,
∴满足题意的m,n的值为:或,
∴或,
当时,C=8×8﹣9×3=64﹣27=37;
当或时,C=15×15﹣16×4=225﹣64=161,
综上可知:C的值为:37或161;
(3)∵(2x+3y+m)2+(3x+2y﹣3m)2,x+y﹣2024≥0,2024﹣x﹣y≥0,
∴x+y﹣2024=2024﹣x﹣y=0,
∴x+y=2024,
∵(2x+3y+m)2+(3x+2y﹣3m)2,
∴(2x+3y+m)2+(3x+2y﹣3m)2=0,
∵(2x+3y+m)2≥0,(3x+2y﹣3m)2≥0,
∴2x+3y+m=0①,3x+2y﹣3m=0②,
①+②得:5x+5y﹣2m=0,
5(x+y)﹣2m=0,
5×2024﹣2m=0,
解得:m=5060,
∴,
即,
∴m的算术平方根的“美好区间”为(71,72).
24.【解答】解:(1)①∵若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.,
∴3,4,7不是“快乐三数组”;
②∵,
∴,,是“快乐三数组”;
③∵,
∴,1,是“快乐三数组”,
故答案为:②③.
(2)若,,1(m≠0)构成“快乐三数组”,则:
,,
①当时,
解得,经检验是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
②时,
解得m=﹣2,经检验m=﹣2是该方程的根,此时,不是正数,不构成“快乐三数组”;
③时,
解得m=1,经检验m=1是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
综上所述:m=1或.
(3)∵∠C=∠D=90°,若AB的长为c,∠C的两条邻边长分别为a,b,
∴a2+b2=c2,且0<c﹣a<b<c+a
∴,
∵c﹣a,b,c+a构成“快乐三数组”,
∴,
∴
,
将a2+b2=c2代入上式,得:,
∴b=2a,
∴,
在Rt△ABD中,BD=AD,
由勾股定理得:AD2+BD2=AB2,
∴,
∴,
∵S△ABD﹣S△ABC=6,
∴,
解得或(不合题意,舍去),
∴AB=a=2.
25.【解答】解:(1)∵A(0,8),B(﹣6,0),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB,
∵四边形ABCD是菱形,
∴BC=AD=AB=10,AD∥BC,
∴OC=BC﹣OB=4,∠OAD=∠AOB=90°.
∴C(4,0),D(10,8).
(2)连接CF,
∵四边形ABCD是菱形,
∴AE=CE,BD⊥AC,
∴AF=CF,
∵∠AOC=90°,
∴AC,CE,
在Rt△OCF中,OF2+OC2=CF2,即(8﹣CF)2+42=CF2,
解得CF=5.
∴EF.
(3)存在.
∵BD⊥AC,
∴如图,当PB∥AC,PC∥BD时,四边形BECP的矩形,
取OA中点G,连接EG.
则OGOA=4,EGOC=2.
∴E(2,4),
由平移可知,将线段EC先向左平移8个单位再向下平移4个单位与线段BP重合(点C与点P重合),
∴P(﹣4,﹣4).
21世纪教育网(www.21cnjy.com)
同课章节目录
