第十七章勾股定理期中复习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理期中复习人教版2024—2025学年八年级下册
一、选择题
1.下列条件中,a、b、c分别为三角形的三边,不能判断△ABC为直角三角形的是( )
A.a2+b2=c2 B.a=2,b=3,c=4
C.a:b:c=1::3 D.∠A+∠B=∠C
2.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD为△ABC的高,则AD的长为( )
A. B. C. D.
4.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
5.如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=十尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,求折断处离地面的高度.设竹子折断处离地面x尺,根据题意,可列方程为( )
A.x2+62=102 B.(10﹣x)2+62=x2
C.x2+(10﹣x)2=62 D.x2+62=(10﹣x)2
6.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A. B.5cm C. D.7cm
二、填空题
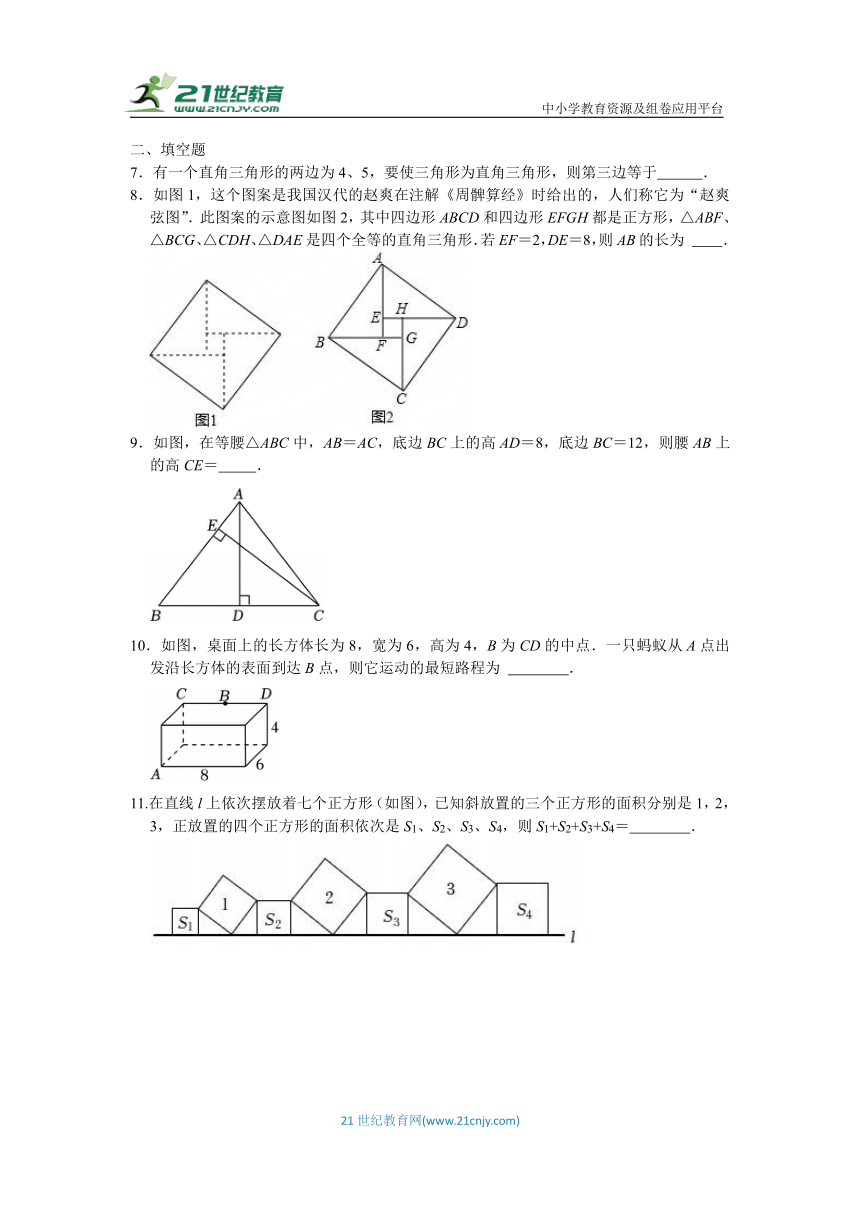
7.有一个直角三角形的两边为4、5,要使三角形为直角三角形,则第三边等于 .
8.如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为 .
9.如图,在等腰△ABC中,AB=AC,底边BC上的高AD=8,底边BC=12,则腰AB上的高CE= .
10.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为 .
11.在直线l上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= .
三、解答题
12.如图,武汉光谷为庆祝“两会”的召开,园艺工人要在二妃山一块Rt△ABC(∠ACB=90°)的空地上划出一个△ADC后,种植出如图中阴影部分图案的草坪.测得CD=1米,AD=2米,米,米.求图中阴影部分的面积.
13.某校为加强学生劳动教育,将劳动基地按班级进行分配,如图是八年级(4)班的劳动实践基地的示意图形状,经过班级同学共同努力,测得AB=4m,AD=3m,BC=12m,CD=13m,∠A=90°.
(1)求B、D之间的距离.
(2)该班计划将该区域全部种植向日葵,若种植向日葵每平方米成本为12元,则该班种植向日葵的成本为多少?
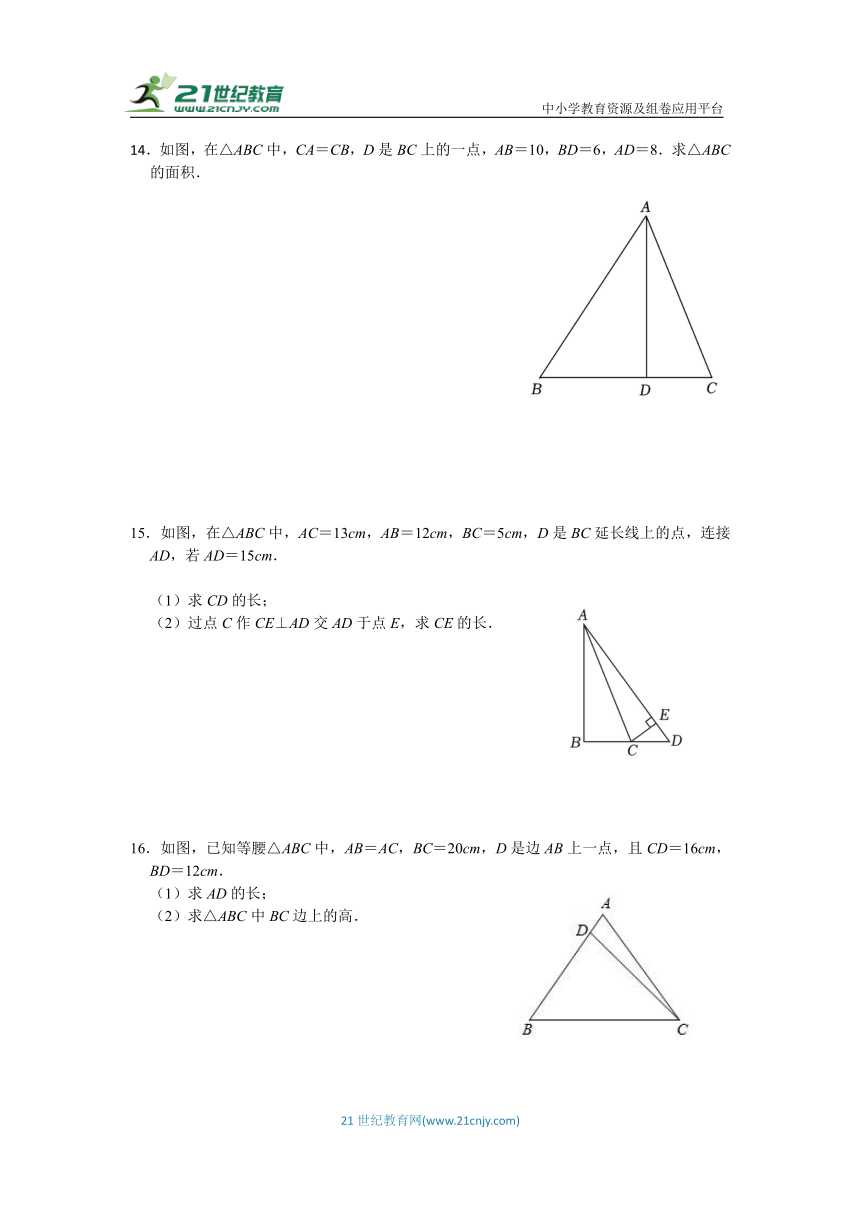
14.如图,在△ABC中,CA=CB,D是BC上的一点,AB=10,BD=6,AD=8.求△ABC的面积.
15.如图,在△ABC中,AC=13cm,AB=12cm,BC=5cm,D是BC延长线上的点,连接AD,若AD=15cm.
(1)求CD的长;
(2)过点C作CE⊥AD交AD于点E,求CE的长.
16.如图,已知等腰△ABC中,AB=AC,BC=20cm,D是边AB上一点,且CD=16cm,BD=12cm.
(1)求AD的长;
(2)求△ABC中BC边上的高.
17.如图,在一条笔直的东西方向的公路上有A、B两地,相距500米,且离公路不远处有一块山地C需要开发,已知C与A地的距离为300米,与B地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C周围半径260米范围内不得进入.
(1)山地C距离公路的垂直距离为多少米?
(2)在进行爆破时,A、B两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.
18.若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.
(1)下列三组数是“快乐三数组”有 ②③ (填序号):
①3,4,7
②,,
③,1,
(2)若,,1(m≠0)构成“快乐三数组”,求m的值.
(3)如图,在四边形ADBC中,∠C=∠D=90°,BD=AD,连接对角线AB,若AB的长为c,∠C的两条邻边长分别为a,b,若c﹣a,b,c+a构成“快乐三数组”,且S△ABD﹣S△ABC=6,求AB的长.
19.阅读材料:对于平面直角坐标系中的任意两点M1(x1,y1),M2(x2,y2),我们把叫做M1,M2两点间的距离,记作d(M1,M2).如A(﹣2,3),B(2,5),则.
请根据以上阅读材料,解答下列问题:
(1)①若,,直接写出d(A,B)的值;
②当A(a,1),B(﹣1,4)的距离d(A,B)=5时,求出a的值;
(2)①若在平面内有一点C(x,y),使式子有最小值,直接写出这个最小值;
②直接写出的最小值.
参考答案
一、选择题
1.【解答】解:A、∵a2+b2=c2,
∴△ABC是直角三角形,
故不符合题意;
B、∵a=2,b=3,c=4,32+22≠42,
∴△ABC不是直角三角形,
故符合题意;
C、∵a:b:c=1::3,a2+b2=c2,
∴△ABC是直角三角形,
故不符合题意;
D、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故不符合题意;
故选:B.
2.【解答】解:∵数轴上的点A,点C表示的实数分别是﹣2,1,
∴AC=1﹣(﹣2)=3,
在Rt△ABC中,由勾股定理得:AB,
∴点P表示的数为2,
故选:A.
3.【解答】解:由勾股定理得:BC,
∵S△ABC=3×32×12×31×3,
又∵S△ABCBC AD,
∴BC AD=7,
∴AD,
故选:A.
4.【解答】解:由勾股定理得,AB2=AC2+BC2=25,
则阴影部分的面积AC×BCπ×()2π×()2π×()2
3×4π(AC2+BC2﹣AB2)
=6,
故选:A.
5.【解答】解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+62=(10﹣x)2.
故选D.
6.【解答】解:侧面展开图如图所示,
∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2,
∴AP==5cm.
故选:B.
二、填空题
7.【解答】解:①若4是直角边,5是斜边,那么第三边3;
②若4和5都是直角边,那么第三边.
故答案是3或.
8.【解答】解:依题意知,BG=AF=DE=8,EF=FG=2
∴BF=BG﹣FG=6,
∴直角△ABF中,利用勾股定理得:AB10.
故答案为:10.
9.【解答】解:∵AB=AC,AD是底边BC上的高,
∴BD=DC=6,
∴AB,
∵,
∴,
∴CE=9.6,
故答案为:9.6.
10.【解答】解:①如图所示,蚂蚁从A出发经过左侧面和上底面到达B点时:
最短路径为:;
②如图所示,蚂蚁从A出发,经过正面和上底面到达B点时:
最短路径为:;
∵
∴最短路径为10,
故答案是:10.
11.【解答】解:如图,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD.
在△ABC和△BED中,
,
∴△ABC≌△BED(AAS),
∴BC=DE.
∵S2=DE2,DE=BC,
∴S2=BC2.
∵S1=AC2,S2=BC2,AC2+BC2=AB2,AB2=1,
∴S1+S2=1.
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
三、解答题
12.【解答】解:在Rt△ABC中,由勾股定理得,
AC(米),
∵CD2+AD2=12+22=5=AC2,
∴△ACD是直角三角形,
∴图中阴影部分的面积=S△ABC﹣S△ACD(1)米2.
13.【解答】解:(1)连接BD,
∵∠A=90°,
∴
=
=5(m),
故B、D之间的距离为5m;
(2)∵52+122=132,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,
∴∠CBD=90°,
∴
=
=432(元),
故则该班种植向日葵的成本为432元.
14.【解答】解:∵BD2+AD2=62+82=100,AB2=102=100,
∴BD2+AD2=AB2.
∴△ABC是直角三角形且∠ADB=90°.
设CA=CB=x,则CD=x﹣6.
在Rt△ADC中,CD2+AD2=AC2.
∴(x﹣6)2+82=x2,解得:,即 .
∴S△ABC=.
15.【解答】解:(1)∵AC=13cm,AB=12cm,BC=5cm,
∴AC2=169,AB2=144,BC2=25,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABD=90°,
在Rt△ABD中,由勾股定理得:,
∴CD=BD﹣BC=9﹣5=4(cm),
∴CD的长为4cm;
(2)由(1)得CD=4cm,∠ABD=90°,
∴AB⊥BD,
∵CE⊥AD,
∴,
∴,
∴15CE=48,
∴,
∴CE的长为cm.
16.【解答】解:(1)∵BC=20cm,且CD=16cm,BD=12cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=90°,
设AD=x cm,则AC=AB=(x+12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即x2+162=(x+12)2,
解得:x=,
即AD=cm;
(2)AB=AC=+12=(cm),
过A作AE⊥BC于E,则AE是△ABC的高,
∵AB=AC,BC=20cm,
∴BE=CE=10(cm),
在Rt△AEB中,由勾股定理得:AE===(cm),
即△ABC中BC边上的高是cm.
17.【解答】解:(1)由题意可知,AC=300米,BC=400米,AB=500米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
如图1,过点C作CD⊥AB于点D,
∴S△ABCAB CDAC BC,
∴CD240(米),
答:山地C距离公路的垂直距离为240米;
(2)公路AB有危险需要暂时封锁,理由如下:
如图2,过C作CD⊥AB于点D,以点C为圆心,260米为半径画弧,交AB于点E、F,连接CE,CF,
则EC=FC=260米,DE=DF,
由(1)可知,CD=240米,
∵240米<260米,
∴有危险需要暂时封锁,
在Rt△CDE中,由勾股定理得:DE100(米),
∴EF=2DE=200(米),
即需要封锁的公路长为200米.
18.【解答】解:(1)①∵若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.,
∴3,4,7不是“快乐三数组”;
②∵,
∴,,是“快乐三数组”;
③∵,
∴,1,是“快乐三数组”,
故答案为:②③.
(2)若,,1(m≠0)构成“快乐三数组”,则:
,,
①当时,
解得,经检验是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
②时,
解得m=﹣2,经检验m=﹣2是该方程的根,此时,不是正数,不构成“快乐三数组”;
③时,
解得m=1,经检验m=1是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
综上所述:m=1或.
(3)∵∠C=∠D=90°,若AB的长为c,∠C的两条邻边长分别为a,b,
∴a2+b2=c2,且0<c﹣a<b<c+a
∴,
∵c﹣a,b,c+a构成“快乐三数组”,
∴,
∴
,
将a2+b2=c2代入上式,得:,
∴b=2a,
∴,
在Rt△ABD中,BD=AD,
由勾股定理得:AD2+BD2=AB2,
∴,
∴,
∵S△ABD﹣S△ABC=6,
∴,
解得或(不合题意,舍去),
∴.
19.【解答】解:(1)①∵A(3,0),B(0,4),
∴d(A,B)5;
②∵A(a,1),B(﹣1,4)的距离d(A,B)=5,
∴5,
∴(a+1)2+(1﹣4)2=52,
解得:a=3 或﹣5;
(2)①如图,点E(﹣3,4),点F(2,4),
∵表示点C(x,y)与点E(﹣3,4)的距离,表示点C(x,y)与点F(2,4)的距离,
∴表示点C与点E、F的距离和,即CE+CF,
当点C在线段EF上时,CE+CF=EF5,
即的最小值为5;
②∵,
设A(m,0),B(3,1),C(0,n),D(2,6).
欲求的最小值,可以把问题转化为求AC+AB+CD的最小值,如图,作点B关于x轴的对称点B′(3,﹣1),点D关于y轴的对称点D′(﹣2,6),连接AB′,CD′,B′D′.
则AB=AB′,CD=CD′,
∵AC+AB+CD=AC+AB′+CD′≥B′D′,
∴AC+AB+CD,
∴的最小值,
∴原式的最小值.
21世纪教育网(www.21cnjy.com)
第十七章勾股定理期中复习人教版2024—2025学年八年级下册
一、选择题
1.下列条件中,a、b、c分别为三角形的三边,不能判断△ABC为直角三角形的是( )
A.a2+b2=c2 B.a=2,b=3,c=4
C.a:b:c=1::3 D.∠A+∠B=∠C
2.如图,数轴上的点A,点C表示的实数分别是﹣2,1,BC⊥AC于点C,且BC=1,连接AB.若以点A为圆心,AB长为半径画弧交数轴于点A右边的点P,则点P所表示的实数为( )
A. B. C. D.
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD为△ABC的高,则AD的长为( )
A. B. C. D.
4.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,分别以各边为直径作半圆,则图中阴影部分的面积为( )
A.6 B. C.4π﹣6 D.
5.如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=十尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,求折断处离地面的高度.设竹子折断处离地面x尺,根据题意,可列方程为( )
A.x2+62=102 B.(10﹣x)2+62=x2
C.x2+(10﹣x)2=62 D.x2+62=(10﹣x)2
6.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A. B.5cm C. D.7cm
二、填空题
7.有一个直角三角形的两边为4、5,要使三角形为直角三角形,则第三边等于 .
8.如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为 .
9.如图,在等腰△ABC中,AB=AC,底边BC上的高AD=8,底边BC=12,则腰AB上的高CE= .
10.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为 .
11.在直线l上依次摆放着七个正方形(如图),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= .
三、解答题
12.如图,武汉光谷为庆祝“两会”的召开,园艺工人要在二妃山一块Rt△ABC(∠ACB=90°)的空地上划出一个△ADC后,种植出如图中阴影部分图案的草坪.测得CD=1米,AD=2米,米,米.求图中阴影部分的面积.
13.某校为加强学生劳动教育,将劳动基地按班级进行分配,如图是八年级(4)班的劳动实践基地的示意图形状,经过班级同学共同努力,测得AB=4m,AD=3m,BC=12m,CD=13m,∠A=90°.
(1)求B、D之间的距离.
(2)该班计划将该区域全部种植向日葵,若种植向日葵每平方米成本为12元,则该班种植向日葵的成本为多少?
14.如图,在△ABC中,CA=CB,D是BC上的一点,AB=10,BD=6,AD=8.求△ABC的面积.
15.如图,在△ABC中,AC=13cm,AB=12cm,BC=5cm,D是BC延长线上的点,连接AD,若AD=15cm.
(1)求CD的长;
(2)过点C作CE⊥AD交AD于点E,求CE的长.
16.如图,已知等腰△ABC中,AB=AC,BC=20cm,D是边AB上一点,且CD=16cm,BD=12cm.
(1)求AD的长;
(2)求△ABC中BC边上的高.
17.如图,在一条笔直的东西方向的公路上有A、B两地,相距500米,且离公路不远处有一块山地C需要开发,已知C与A地的距离为300米,与B地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C周围半径260米范围内不得进入.
(1)山地C距离公路的垂直距离为多少米?
(2)在进行爆破时,A、B两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.
18.若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.
(1)下列三组数是“快乐三数组”有 ②③ (填序号):
①3,4,7
②,,
③,1,
(2)若,,1(m≠0)构成“快乐三数组”,求m的值.
(3)如图,在四边形ADBC中,∠C=∠D=90°,BD=AD,连接对角线AB,若AB的长为c,∠C的两条邻边长分别为a,b,若c﹣a,b,c+a构成“快乐三数组”,且S△ABD﹣S△ABC=6,求AB的长.
19.阅读材料:对于平面直角坐标系中的任意两点M1(x1,y1),M2(x2,y2),我们把叫做M1,M2两点间的距离,记作d(M1,M2).如A(﹣2,3),B(2,5),则.
请根据以上阅读材料,解答下列问题:
(1)①若,,直接写出d(A,B)的值;
②当A(a,1),B(﹣1,4)的距离d(A,B)=5时,求出a的值;
(2)①若在平面内有一点C(x,y),使式子有最小值,直接写出这个最小值;
②直接写出的最小值.
参考答案
一、选择题
1.【解答】解:A、∵a2+b2=c2,
∴△ABC是直角三角形,
故不符合题意;
B、∵a=2,b=3,c=4,32+22≠42,
∴△ABC不是直角三角形,
故符合题意;
C、∵a:b:c=1::3,a2+b2=c2,
∴△ABC是直角三角形,
故不符合题意;
D、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
故不符合题意;
故选:B.
2.【解答】解:∵数轴上的点A,点C表示的实数分别是﹣2,1,
∴AC=1﹣(﹣2)=3,
在Rt△ABC中,由勾股定理得:AB,
∴点P表示的数为2,
故选:A.
3.【解答】解:由勾股定理得:BC,
∵S△ABC=3×32×12×31×3,
又∵S△ABCBC AD,
∴BC AD=7,
∴AD,
故选:A.
4.【解答】解:由勾股定理得,AB2=AC2+BC2=25,
则阴影部分的面积AC×BCπ×()2π×()2π×()2
3×4π(AC2+BC2﹣AB2)
=6,
故选:A.
5.【解答】解:设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+62=(10﹣x)2.
故选D.
6.【解答】解:侧面展开图如图所示,
∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2,
∴AP==5cm.
故选:B.
二、填空题
7.【解答】解:①若4是直角边,5是斜边,那么第三边3;
②若4和5都是直角边,那么第三边.
故答案是3或.
8.【解答】解:依题意知,BG=AF=DE=8,EF=FG=2
∴BF=BG﹣FG=6,
∴直角△ABF中,利用勾股定理得:AB10.
故答案为:10.
9.【解答】解:∵AB=AC,AD是底边BC上的高,
∴BD=DC=6,
∴AB,
∵,
∴,
∴CE=9.6,
故答案为:9.6.
10.【解答】解:①如图所示,蚂蚁从A出发经过左侧面和上底面到达B点时:
最短路径为:;
②如图所示,蚂蚁从A出发,经过正面和上底面到达B点时:
最短路径为:;
∵
∴最短路径为10,
故答案是:10.
11.【解答】解:如图,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD.
在△ABC和△BED中,
,
∴△ABC≌△BED(AAS),
∴BC=DE.
∵S2=DE2,DE=BC,
∴S2=BC2.
∵S1=AC2,S2=BC2,AC2+BC2=AB2,AB2=1,
∴S1+S2=1.
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
三、解答题
12.【解答】解:在Rt△ABC中,由勾股定理得,
AC(米),
∵CD2+AD2=12+22=5=AC2,
∴△ACD是直角三角形,
∴图中阴影部分的面积=S△ABC﹣S△ACD(1)米2.
13.【解答】解:(1)连接BD,
∵∠A=90°,
∴
=
=5(m),
故B、D之间的距离为5m;
(2)∵52+122=132,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,
∴∠CBD=90°,
∴
=
=432(元),
故则该班种植向日葵的成本为432元.
14.【解答】解:∵BD2+AD2=62+82=100,AB2=102=100,
∴BD2+AD2=AB2.
∴△ABC是直角三角形且∠ADB=90°.
设CA=CB=x,则CD=x﹣6.
在Rt△ADC中,CD2+AD2=AC2.
∴(x﹣6)2+82=x2,解得:,即 .
∴S△ABC=.
15.【解答】解:(1)∵AC=13cm,AB=12cm,BC=5cm,
∴AC2=169,AB2=144,BC2=25,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABD=90°,
在Rt△ABD中,由勾股定理得:,
∴CD=BD﹣BC=9﹣5=4(cm),
∴CD的长为4cm;
(2)由(1)得CD=4cm,∠ABD=90°,
∴AB⊥BD,
∵CE⊥AD,
∴,
∴,
∴15CE=48,
∴,
∴CE的长为cm.
16.【解答】解:(1)∵BC=20cm,且CD=16cm,BD=12cm,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=90°,
设AD=x cm,则AC=AB=(x+12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即x2+162=(x+12)2,
解得:x=,
即AD=cm;
(2)AB=AC=+12=(cm),
过A作AE⊥BC于E,则AE是△ABC的高,
∵AB=AC,BC=20cm,
∴BE=CE=10(cm),
在Rt△AEB中,由勾股定理得:AE===(cm),
即△ABC中BC边上的高是cm.
17.【解答】解:(1)由题意可知,AC=300米,BC=400米,AB=500米,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
如图1,过点C作CD⊥AB于点D,
∴S△ABCAB CDAC BC,
∴CD240(米),
答:山地C距离公路的垂直距离为240米;
(2)公路AB有危险需要暂时封锁,理由如下:
如图2,过C作CD⊥AB于点D,以点C为圆心,260米为半径画弧,交AB于点E、F,连接CE,CF,
则EC=FC=260米,DE=DF,
由(1)可知,CD=240米,
∵240米<260米,
∴有危险需要暂时封锁,
在Rt△CDE中,由勾股定理得:DE100(米),
∴EF=2DE=200(米),
即需要封锁的公路长为200米.
18.【解答】解:(1)①∵若任意三个正数a,b,c满足:的关系,则称这三个正数为“快乐三数组”.,
∴3,4,7不是“快乐三数组”;
②∵,
∴,,是“快乐三数组”;
③∵,
∴,1,是“快乐三数组”,
故答案为:②③.
(2)若,,1(m≠0)构成“快乐三数组”,则:
,,
①当时,
解得,经检验是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
②时,
解得m=﹣2,经检验m=﹣2是该方程的根,此时,不是正数,不构成“快乐三数组”;
③时,
解得m=1,经检验m=1是该方程的根,此时,,1三个数都是正数,构成“快乐三数组”;
综上所述:m=1或.
(3)∵∠C=∠D=90°,若AB的长为c,∠C的两条邻边长分别为a,b,
∴a2+b2=c2,且0<c﹣a<b<c+a
∴,
∵c﹣a,b,c+a构成“快乐三数组”,
∴,
∴
,
将a2+b2=c2代入上式,得:,
∴b=2a,
∴,
在Rt△ABD中,BD=AD,
由勾股定理得:AD2+BD2=AB2,
∴,
∴,
∵S△ABD﹣S△ABC=6,
∴,
解得或(不合题意,舍去),
∴.
19.【解答】解:(1)①∵A(3,0),B(0,4),
∴d(A,B)5;
②∵A(a,1),B(﹣1,4)的距离d(A,B)=5,
∴5,
∴(a+1)2+(1﹣4)2=52,
解得:a=3 或﹣5;
(2)①如图,点E(﹣3,4),点F(2,4),
∵表示点C(x,y)与点E(﹣3,4)的距离,表示点C(x,y)与点F(2,4)的距离,
∴表示点C与点E、F的距离和,即CE+CF,
当点C在线段EF上时,CE+CF=EF5,
即的最小值为5;
②∵,
设A(m,0),B(3,1),C(0,n),D(2,6).
欲求的最小值,可以把问题转化为求AC+AB+CD的最小值,如图,作点B关于x轴的对称点B′(3,﹣1),点D关于y轴的对称点D′(﹣2,6),连接AB′,CD′,B′D′.
则AB=AB′,CD=CD′,
∵AC+AB+CD=AC+AB′+CD′≥B′D′,
∴AC+AB+CD,
∴的最小值,
∴原式的最小值.
21世纪教育网(www.21cnjy.com)
同课章节目录
