第十八章平行四边形期中压轴题训练(含解析)
文档属性
| 名称 | 第十八章平行四边形期中压轴题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1022.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 17:51:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形期中压轴题训练人教版2024—2025学年八年级下册
一、选择题
1.如图,在正方形ABCD中,E为BC边上一动点(点E、B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.若AB=2时,则△ADP周长的最小值为( )
A. B. C. D.
2.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长( )
A. B. C. D.
3.我国清代数学家李悦借助三个正方形用出入相补的方法证明了勾股定理.如图,直角三角形的三边a,b,c满足c>a>b,分别以a、b、c为边作三个正方形:正方形CBFG、正方形HDEF、正方形ABEJ,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若a+b=7,四边形ABFK与△DEL面积之和为7,则正方形ABEJ的面积为( )
A.49 B.28 C.21 D.14
4.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
5.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5 C.2.4 D.1.2
6.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:①△DOF≌△COE;②CF=BE;③FO=FG;④四边形CEOF的面积为正方形ABCD面积的;⑤OF2+OE2=EF2.其中正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题
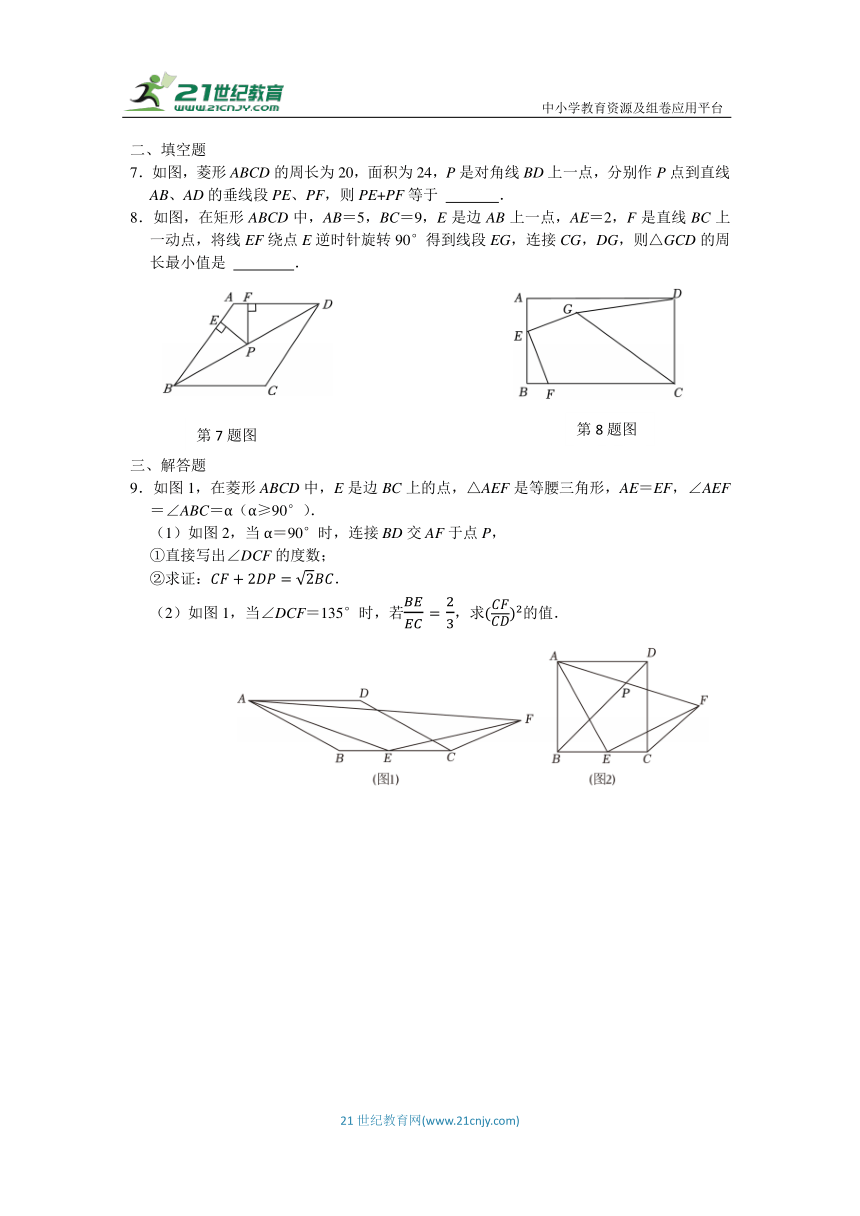
7.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
8.如图,在矩形ABCD中,AB=5,BC=9,E是边AB上一点,AE=2,F是直线BC上一动点,将线EF绕点E逆时针旋转90°得到线段EG,连接CG,DG,则△GCD的周长最小值是 .
三、解答题
9.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
10.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
11.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
12.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
13.如图1,在 ABCD中,点E为AD中点,BA,CE的延长线交于点F.
(1)求证:BA=AF.
(2)若∠BCF=∠DCF时,记AB与CD之间的距离为h1,AD与BC之间的距离为h2,求h1:h2的值.
(3)如图2,连结AC,BD,在(2)的条件下,求证:AC2+BD2=10AB2.
14.如图,在平行四边形ABCD中,点E在BC边上,且AD=DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠AFD=∠ECD;
(2)求证:△AFD≌△DCE;
(3)若∠B=60°,CD=DF,BE=2,求AE.
15.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
16.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
参考答案
一、选择题
1.解:如图所示,在AB上取一点G使得BG=BE,连接EG,CP,
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=2,∠B=∠BCD=90°,
∴∠BAE+∠BEA=90°=∠BEA+∠CEP,
∴∠GAE=∠CEP,
∵BG=BE,
∴∠BGE=∠BEG=45°,
∴∠AGE=90°,
∵AB﹣BG=BC﹣BE,
∴AG=EC,
又∵AE=EP,
∴△AGE≌△ECP(SAS),
∴∠ECP=∠AGE=135°,
∴∠DCP=45°,
∴点P在直线CP上运动,
如图所示,作点D关于直线CP的对称点F,连接 CF,AF,PF,
∴DP=FP,CF=CD=2,∠DCP=∠FCP=45°,即∠DCF=90°,
∴∠DCF+∠BCD=180°,
即B、C、F三点共线,
∵△ADP的周长=AD+DP+AP=2+DP+AP=AP+PF+2,
∴当A、P、F三点共线时,△ADP的周长有最小值,最小值为AF+2,
在Rt△ABC中,由勾股定理得 ,
∴△ADP的周长最小值为 ,
故选:A.
2.解:将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,如图:
∴EO=OD=4,MO(EF+CD)=4,
∵点N、M分别是AD、FC的中点,
∴AN=ND=3,
∴ON=OD﹣ND=4﹣3=1.
在Rt△MON中,MN2=MO2+ON2,即MN.
故选:C.
3.解:如图,作JP⊥EG于点P,则∠JPK=∠JPE=90°,
∵四边形BCGF、四边形ABEJ、四边形DEFH都是正方形,
∴BA=BE,BC=BE,EJ=BE,∠CBF=∠ABE=∠BEJ=∠BFE=∠D=90°.
∴Rt△ABC≌Rt△EBF.
∴EF=CA=b.
∵∠EPJ=∠BFE=90°,
∴∠PJE=∠FEB=90°﹣∠PEJ,
又∵EJ=BE,
∴△EJP≌△BEF.
∴JP=EF=ED=b,PE=FB=a,
∴S△EJP+S△BEFabab=ab.
∵∠PJK+∠PJE=90°,∠DEL+∠FEB=90°,
∴∠PJK=∠DEL,
∵∠JPK=∠D=90°,
∴△PJK≌△DEL.
∴S△PJK=S△DEL,
∵S四边形ABFK+S△DEL=7,
∴S四边形ABFK+S△PJK=7,
∵BA=c,S正方形BEJA﹣(S△EJP+S△BEF)=S四边形ABFK+S△PJK,
∴c2﹣ab=7,
∵a2+b2=c2,
∴a2+b2﹣ab=7.
∴(a+b)2﹣3ab=7.
∵a+b=7,
∴49﹣3ab=7.
∴ab=14.
∴S正方形ABEJ=c2=7+ab=21.
故选:C.
4.解:如图,连接MN,过点A作AF⊥BC于F,
∵AB=AC,BC=10cm,
∴BFBC=5cm,
由勾股定理得:AF12(cm),
∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∴MNBC=5cm,MN∥BC,
∴图中阴影部分可以看作三个以5cm为底,且高的和为12cm的三角形,
∴S阴影部分5×12=30(cm2),
故选:B.
5.解:如图,连接CP.
∵∠C=90°,AC=3,BC=4,
∴AB5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,
此时,S△ABCBC ACAB CP,
即4×35 CP,
解得CP=2.4.
故选:C.
6.解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③∵△COE≌△DOF,
∴FO=EO,
∵∠OFE=∠ODF=45°,
∴∠DOF=∠CFE,
设∠DOF=α,
∴∠OGF=45°+α,
∵∠COF=90°﹣α,
当45°+α=90°﹣α时,α=22.5°,OF=FG,
故③不正确;
④由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故④正确;
⑤在Rt△ECF中,∠EOF=90°,
根据勾股定理,得:OE2+OF2=EF2,
故⑤正确;
综上所述,正确的是①②④⑤,
故选:C.
二、填空题
7.解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
8.解:如图,将BE绕点E逆时针旋转90°得到EH,连接GH,并延长交BC于N,
∵AB=5,AE=2,
∴BE=3,
∵将线EF绕点E逆时针旋转90°得到线段EG,
∴EF=EG,∠GEF=90°,
∵将BE绕点E逆时针旋转90°得到EH,
∴BE=EH=3,∠BEH=90°=∠GEF,
∴∠GEH=∠BEF,
在△BEF和△HEG中,
,
∴△BEF≌△HEG(SAS),
∴∠EBF=∠EHG=90°,BF=GH,
∴点G在过点H且垂直EH的直线上运动,
作点C关于直线GH的对称点C',连接C'D,则CG+DG的最小值为C'D的长,
∵∠ABC=∠BEH=90°,∠EHN=90°,
∴四边形EBNH是矩形,
∴BN=EH=3,
∴CN=6,
∴CC'=12,
∴C'D13,
∴CG+DG的最小值为13,
∵CD=AB=5,
∴△GCD的周长最小值是13+5=18,
故答案为:18.
三、解答题
9.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
10.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
11.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
12.【解答】(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
在Rt△ABC中,
∵AB=BC=6,
∴AC12,
∴AO=DOAC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK3.
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠F=∠ECD,∠FAE=∠D,
∵E为AD的中点,
∴AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AB=AF;
(2)解:由(1)知AB∥CD,
∴∠F=∠DCE,
∵∠BCF=∠DCF,
∴∠F=∠BCF,
∴BF=BC,
∵AB=AF,
∴BC=2AB,
∵,
∴h1:h2=BC:AB=2;
(3)证明:过点A作AM⊥BC于点M,DN⊥BC,交BC的延长线于点N,
∵AB∥CD,
∴∠B=∠DCN,
∵AB=CD,∠AMB=∠DNC,
∴△ABM≌△DCN(AAS),
∴BM=CN,AM=DN=h2,
在Rt△DBN中,DB2=DN2+BN2=DN2+(BC+CN)2,
在Rt△ACM中,AC2=AM2+(BC﹣BM)2=DN2+(BC﹣CN)2,
∴AC2+BD2=2DN2+(BC+CN)2+(BC﹣CN)2
=2DN2+2BC2+2CN2
=2DC2+2BC2,
由(2)知,BC=2AB,
∴AC2+BD2=2AB2+8AB2=10AB2.
14.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠ECD=180°,
∵∠AFE=∠B,
∴∠AFE+∠ECD=180°,
又∵∠AFE+∠AFD=180°,
∴∠AFD=∠ECD;
(2)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC,
在△AFD和△DCE中,
,
∴△AFD≌△DCE(AAS),
(3)解:过点E作EH⊥AB于H,如图所示:
由(2)可知:△AFD≌△DCE,
∴DF=CE,AF=CD,
∵四边形ABCD为平行四边形,
∴BC=AD,AB=CD,
∵AD=DE,
∴BC=DE,
∵DE=DF+EF=CE+EF,BC=CE+BE,
∴BE=EF,
∵AB=CD,CD=DF,AF=CD,DF=CE,
∴AB=AF=CD=CE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SSS),
∴∠AEB=∠AEF,
∴∠B=60°,
∴∠C=180°﹣∠B=120°,
∵CD=CE,
∴∠CED=∠CDE(180°﹣∠C)=30°,
∴∠BEF=180°﹣∠CED=150°,
∴∠AEB=∠AEF∠BEF=75°,
∵EH⊥AB,∠B=60°,
∴∠BEH=30°,
∴∠AEH=∠AEB﹣∠BEH=45°,
∴△AHE为等腰直角三角形,即HE=HA,
在Rt△BEH中,∠∠BEH=30°,BE=2,
∴BHBE=1,
由勾股定理得:HE,
∴HE=HA,
∴AE.
15.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
16.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
21世纪教育网(www.21cnjy.com)
第十八章平行四边形期中压轴题训练人教版2024—2025学年八年级下册
一、选择题
1.如图,在正方形ABCD中,E为BC边上一动点(点E、B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.若AB=2时,则△ADP周长的最小值为( )
A. B. C. D.
2.如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上平移,在平移过程中,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长( )
A. B. C. D.
3.我国清代数学家李悦借助三个正方形用出入相补的方法证明了勾股定理.如图,直角三角形的三边a,b,c满足c>a>b,分别以a、b、c为边作三个正方形:正方形CBFG、正方形HDEF、正方形ABEJ,把它们拼成如图所示形状,使E、F、G三点在一条直线上,若a+b=7,四边形ABFK与△DEL面积之和为7,则正方形ABEJ的面积为( )
A.49 B.28 C.21 D.14
4.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
5.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是( )
A.2.5 B.5 C.2.4 D.1.2
6.如图,在正方形ABCD中,点O是对角线AC,BD交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.有下列结论:①△DOF≌△COE;②CF=BE;③FO=FG;④四边形CEOF的面积为正方形ABCD面积的;⑤OF2+OE2=EF2.其中正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题
7.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
8.如图,在矩形ABCD中,AB=5,BC=9,E是边AB上一点,AE=2,F是直线BC上一动点,将线EF绕点E逆时针旋转90°得到线段EG,连接CG,DG,则△GCD的周长最小值是 .
三、解答题
9.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
10.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
11.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
12.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段DG与BE、AE分别相交于点H、K.
(1)求证:△EAB≌△GAD;
(2)判断BE与DG的位置关系,并说明理由;
(3)若AB=6,AG=6,求DK的长.
13.如图1,在 ABCD中,点E为AD中点,BA,CE的延长线交于点F.
(1)求证:BA=AF.
(2)若∠BCF=∠DCF时,记AB与CD之间的距离为h1,AD与BC之间的距离为h2,求h1:h2的值.
(3)如图2,连结AC,BD,在(2)的条件下,求证:AC2+BD2=10AB2.
14.如图,在平行四边形ABCD中,点E在BC边上,且AD=DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠AFD=∠ECD;
(2)求证:△AFD≌△DCE;
(3)若∠B=60°,CD=DF,BE=2,求AE.
15.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
16.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
参考答案
一、选择题
1.解:如图所示,在AB上取一点G使得BG=BE,连接EG,CP,
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=2,∠B=∠BCD=90°,
∴∠BAE+∠BEA=90°=∠BEA+∠CEP,
∴∠GAE=∠CEP,
∵BG=BE,
∴∠BGE=∠BEG=45°,
∴∠AGE=90°,
∵AB﹣BG=BC﹣BE,
∴AG=EC,
又∵AE=EP,
∴△AGE≌△ECP(SAS),
∴∠ECP=∠AGE=135°,
∴∠DCP=45°,
∴点P在直线CP上运动,
如图所示,作点D关于直线CP的对称点F,连接 CF,AF,PF,
∴DP=FP,CF=CD=2,∠DCP=∠FCP=45°,即∠DCF=90°,
∴∠DCF+∠BCD=180°,
即B、C、F三点共线,
∵△ADP的周长=AD+DP+AP=2+DP+AP=AP+PF+2,
∴当A、P、F三点共线时,△ADP的周长有最小值,最小值为AF+2,
在Rt△ABC中,由勾股定理得 ,
∴△ADP的周长最小值为 ,
故选:A.
2.解:将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,如图:
∴EO=OD=4,MO(EF+CD)=4,
∵点N、M分别是AD、FC的中点,
∴AN=ND=3,
∴ON=OD﹣ND=4﹣3=1.
在Rt△MON中,MN2=MO2+ON2,即MN.
故选:C.
3.解:如图,作JP⊥EG于点P,则∠JPK=∠JPE=90°,
∵四边形BCGF、四边形ABEJ、四边形DEFH都是正方形,
∴BA=BE,BC=BE,EJ=BE,∠CBF=∠ABE=∠BEJ=∠BFE=∠D=90°.
∴Rt△ABC≌Rt△EBF.
∴EF=CA=b.
∵∠EPJ=∠BFE=90°,
∴∠PJE=∠FEB=90°﹣∠PEJ,
又∵EJ=BE,
∴△EJP≌△BEF.
∴JP=EF=ED=b,PE=FB=a,
∴S△EJP+S△BEFabab=ab.
∵∠PJK+∠PJE=90°,∠DEL+∠FEB=90°,
∴∠PJK=∠DEL,
∵∠JPK=∠D=90°,
∴△PJK≌△DEL.
∴S△PJK=S△DEL,
∵S四边形ABFK+S△DEL=7,
∴S四边形ABFK+S△PJK=7,
∵BA=c,S正方形BEJA﹣(S△EJP+S△BEF)=S四边形ABFK+S△PJK,
∴c2﹣ab=7,
∵a2+b2=c2,
∴a2+b2﹣ab=7.
∴(a+b)2﹣3ab=7.
∵a+b=7,
∴49﹣3ab=7.
∴ab=14.
∴S正方形ABEJ=c2=7+ab=21.
故选:C.
4.解:如图,连接MN,过点A作AF⊥BC于F,
∵AB=AC,BC=10cm,
∴BFBC=5cm,
由勾股定理得:AF12(cm),
∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∴MNBC=5cm,MN∥BC,
∴图中阴影部分可以看作三个以5cm为底,且高的和为12cm的三角形,
∴S阴影部分5×12=30(cm2),
故选:B.
5.解:如图,连接CP.
∵∠C=90°,AC=3,BC=4,
∴AB5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,
此时,S△ABCBC ACAB CP,
即4×35 CP,
解得CP=2.4.
故选:C.
6.解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
在△COE和△DOF中,
,
∴△COE≌△DOF(ASA),故①正确;
②∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,故②正确;
③∵△COE≌△DOF,
∴FO=EO,
∵∠OFE=∠ODF=45°,
∴∠DOF=∠CFE,
设∠DOF=α,
∴∠OGF=45°+α,
∵∠COF=90°﹣α,
当45°+α=90°﹣α时,α=22.5°,OF=FG,
故③不正确;
④由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故④正确;
⑤在Rt△ECF中,∠EOF=90°,
根据勾股定理,得:OE2+OF2=EF2,
故⑤正确;
综上所述,正确的是①②④⑤,
故选:C.
二、填空题
7.解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
8.解:如图,将BE绕点E逆时针旋转90°得到EH,连接GH,并延长交BC于N,
∵AB=5,AE=2,
∴BE=3,
∵将线EF绕点E逆时针旋转90°得到线段EG,
∴EF=EG,∠GEF=90°,
∵将BE绕点E逆时针旋转90°得到EH,
∴BE=EH=3,∠BEH=90°=∠GEF,
∴∠GEH=∠BEF,
在△BEF和△HEG中,
,
∴△BEF≌△HEG(SAS),
∴∠EBF=∠EHG=90°,BF=GH,
∴点G在过点H且垂直EH的直线上运动,
作点C关于直线GH的对称点C',连接C'D,则CG+DG的最小值为C'D的长,
∵∠ABC=∠BEH=90°,∠EHN=90°,
∴四边形EBNH是矩形,
∴BN=EH=3,
∴CN=6,
∴CC'=12,
∴C'D13,
∴CG+DG的最小值为13,
∵CD=AB=5,
∴△GCD的周长最小值是13+5=18,
故答案为:18.
三、解答题
9.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
10.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
11.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
12.【解答】(1)证明:∵四边形ABCD、四边形AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠DAB+∠DAE=∠EAG+∠DAE,
∴∠EAB=∠GAD,
∵AB=AD,AE=AG,
∴△EAB≌△GAD(SAS).
(2)解:BE⊥DG,理由如下:
∵△EAB≌△GAD,
∴∠AGD=∠AEB,
∵∠AKG=∠HKE,
在Rt△AGK中,∠AGK+∠AKG=90°
∴∠KEH+∠HKE=90°,
∴∠EHK=180°﹣90°=90°,
∴BE⊥DG.
(3)解:连接DE,如图,
在Rt△ABC中,
∵AB=BC=6,
∴AC12,
∴AO=DOAC=6,
∵AG=AE=AO=DO=6.AO⊥DO,
∴四边形AEDO是正方形,
∵∠DEK=∠GAK=90°,
∵DE=AG=6,∠DKE=∠AKG,
∴△DKE≌△GAK(AAS),
∴EK=AK=3,
在Rt△DKE中,
DK3.
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠F=∠ECD,∠FAE=∠D,
∵E为AD的中点,
∴AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AB=AF;
(2)解:由(1)知AB∥CD,
∴∠F=∠DCE,
∵∠BCF=∠DCF,
∴∠F=∠BCF,
∴BF=BC,
∵AB=AF,
∴BC=2AB,
∵,
∴h1:h2=BC:AB=2;
(3)证明:过点A作AM⊥BC于点M,DN⊥BC,交BC的延长线于点N,
∵AB∥CD,
∴∠B=∠DCN,
∵AB=CD,∠AMB=∠DNC,
∴△ABM≌△DCN(AAS),
∴BM=CN,AM=DN=h2,
在Rt△DBN中,DB2=DN2+BN2=DN2+(BC+CN)2,
在Rt△ACM中,AC2=AM2+(BC﹣BM)2=DN2+(BC﹣CN)2,
∴AC2+BD2=2DN2+(BC+CN)2+(BC﹣CN)2
=2DN2+2BC2+2CN2
=2DC2+2BC2,
由(2)知,BC=2AB,
∴AC2+BD2=2AB2+8AB2=10AB2.
14.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠ECD=180°,
∵∠AFE=∠B,
∴∠AFE+∠ECD=180°,
又∵∠AFE+∠AFD=180°,
∴∠AFD=∠ECD;
(2)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC,
在△AFD和△DCE中,
,
∴△AFD≌△DCE(AAS),
(3)解:过点E作EH⊥AB于H,如图所示:
由(2)可知:△AFD≌△DCE,
∴DF=CE,AF=CD,
∵四边形ABCD为平行四边形,
∴BC=AD,AB=CD,
∵AD=DE,
∴BC=DE,
∵DE=DF+EF=CE+EF,BC=CE+BE,
∴BE=EF,
∵AB=CD,CD=DF,AF=CD,DF=CE,
∴AB=AF=CD=CE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SSS),
∴∠AEB=∠AEF,
∴∠B=60°,
∴∠C=180°﹣∠B=120°,
∵CD=CE,
∴∠CED=∠CDE(180°﹣∠C)=30°,
∴∠BEF=180°﹣∠CED=150°,
∴∠AEB=∠AEF∠BEF=75°,
∵EH⊥AB,∠B=60°,
∴∠BEH=30°,
∴∠AEH=∠AEB﹣∠BEH=45°,
∴△AHE为等腰直角三角形,即HE=HA,
在Rt△BEH中,∠∠BEH=30°,BE=2,
∴BHBE=1,
由勾股定理得:HE,
∴HE=HA,
∴AE.
15.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
16.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
21世纪教育网(www.21cnjy.com)
同课章节目录
