2025年九年级数学三轮冲刺训练图形的变换之旋转模型(含解析)
文档属性
| 名称 | 2025年九年级数学三轮冲刺训练图形的变换之旋转模型(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 07:27:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学三轮冲刺训练图形的变换之旋转模型
1.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD.把AD绕点A逆时针旋转90°,得到AE,连接CE、DE.
(1)求证:△ABD≌△ACE;
(2)若,时,求BD的长.
2.如图,在正方形ABCD中,点E在边AB上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边BC的延长线上,连接DE,DF,EF.
(1)判断△DEF的形状,并证明;
(2)若,求△DEF的面积.
3.如图,将矩形ABCD绕点C顺时针旋转,得到矩形FGCE,使得点E落在边AB上,AB的延长线交EG于H,连接DE,DH.
(1)求证:ED平分∠AEC;
(2)求证:EC与DH互相平分.
4.如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
5.如图,在 ABCD中,AB=6,AD=10,∠BAD=60°,P为边AB上的动点.连接PC,将PC绕点P逆时针旋转60°得到PE,过点E作EF∥AB,EF交直线AD于点F.连接PF、DE,分别取PF、DE的中点M、N,连接MN,交AD于点Q.
(1)若点P与点B重合,则线段MN的长度为 .
(2)随着点P的运动,MN与AQ的长度是否发生变化?若不变,求出MN与AQ的长度;若改变,请说明理由.
6.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知BH=7,BC=13,求DH的长.
7.如图,四边形ABCD中,对角线AC与BD交于点O,且OA=OB=OC=ODAB.
(1)求证:四边形ABCD是正方形;
(2)若H是边AB上一点(H与A,B不重合),连接DH,将线段DH绕点H顺时针旋转90°,得到线段HE,过点E分别作BC及AB延长线的垂线,垂足分别为F,G.设四边形BGEF的面积为s1,以HB,BC为邻边的矩形的面积为s2,且s1=s2.当AB=2时,求AH的长.
8.正方形ABCD的边长为4,E、F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:△DEF≌△DMF;
(2)若AE=1,求EF的长.
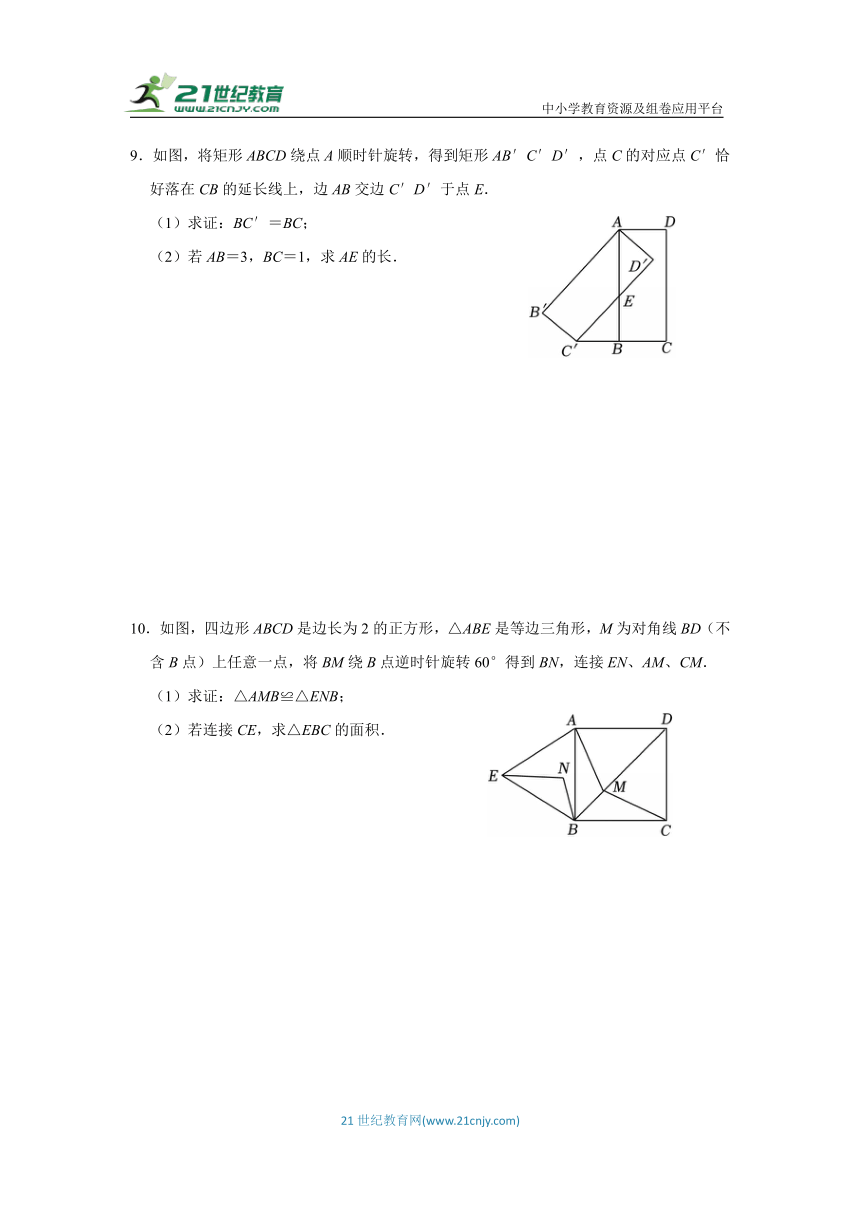
9.如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
(1)求证:BC′=BC;
(2)若AB=3,BC=1,求AE的长.
10.如图,四边形ABCD是边长为2的正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕B点逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)若连接CE,求△EBC的面积.
11.在△ABC中,∠ABC=90°,AB=BC.
(1)如图1,若点D是△ABC内一点,DA=1,DB=2,DC=3.将△CBD绕点B逆时针旋转90°至△ABE,连接DE.判断△ADE的形状(要说明理由),并求∠ADB的度数;
(2)如图2,若点D是△ABC外一点,DA=2,,DC=2,求∠ADB的度数.
12.如图,等边△ABC,在BC边延长线上取点D,连接AD,将线段AD绕点D顺时针旋转60°得到线段DE,连接CE,AE.
(1)求∠ECD的度数;
(2)若AB=6,CD=2,求DE的长.
13.如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBF.延长AE交CF于点G,连接DE.
(1)试判断四边形BEGF的形状,并说明理由;
(2)若BE=2,CG=1,求DE.
14.如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
15.如图1,矩形ABCD中,AB=5,AD=3,将△ABC绕点A旋转到△AB'C'位置,设AC'交直线CD于点M.
(1)当点B'恰好落在DC边上时,求△AB'C'与矩形ABCD重叠部分的面积;
(2)如图2,当点C、B'、C'恰好在一直线上时,求DM的长度.
参考答案
1.【解答】(1)证明:由题意可得:AD=AE,∠DAE=90°,
∵∠BAC=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:设BD=x,
∵∠BAC=90°,,
∴∠ABD=∠ACD=45°,BC=4,
∵△ABD≌△ACE,
∴BD=CE=x,∠ABD=∠ACE=45°,
∴∠DCE=90°,
∴CD2+CE2=DE2,
∴,
解得x1=1,x2=3,
∴BD=1或3.
2.【解答】解:(1)△DEF是等腰直角三角形,
证明:在正方形ABCD中,DA=DC,∠ADC=∠DAB=∠DCB=90°,
∵F落在边BC的延长线上,
∴∠DCF=∠DAB=90°,
∵将点E绕点D逆时针旋转得到点F,
∴DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠ADE=∠CDF,
∵∠ADC=∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)∵△DEF是等腰直角三角形,
∴DE=DF,
∵,,
∴DE=DF=6,
∴△DEF的面积为.
3.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AED=∠EDC.
∵CE=CD,
∴∠CED=∠EDC,
∴∠AED=∠CED,
∴ED平分∠AEC.
(2)证明:连接HC,
∵四边形EFGC为矩形,
∴FG∥EC,
∴∠FHE=∠BEC.
∵∠F=∠EBC=90°,EF=CB,
在△EFH和△CBE中,
∴△EFH≌△CBE(AAS),
∴EH=EC.
结合EC=DC,知EH=DC.
则EH∥DC.
∴四边形EHCD为平行四边形,
∴EC与DH互相平分.
4.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC,∠ACD=45°,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB,
∴FH=CH=x,
∴CFFHx,
∴OE2﹣CF=x2x=(x)2,
∵点E在线段AO上(与端点不重合),
∴0<x,
∴当x时,OE2﹣CF的最小值是.
5.【解答】解:(1)当点P与点B重合时,点F在点D处,此时E、N、D、F、C共线,
如图①,在平行四边形ABCD中,BC=AD=10.
将PC绕点P逆时针旋转60°得到PE,PC=BC=PE=10.
点M、N分别是PF、ED的中点,由中位线可知2MN=PE=10.
∴MN=5.
故答案为:5.
(2)结论:不变.
如解图②,连接FN并延长到点G,使得FN=GN,连接 GE,DG,
∵点N为 DE中点,
∴EN=DN.
∴四边形GEFD 为平行四边形,
∴GE//AF,GD//EF.
延长EG,BA交于H点,连接PG.
∵GD//EF//HB,HG//AF.
∴四边形HADG为平行四边形,
∴HG=AD,
∴∠BAD=∠AHG=60°.
如解图②,延长AB至点K,使得BK=BC,连接CK,
在平行四边形ABCD中,
∵∠BAD=60°,
∴∠CBK=60°,
∴△BKC是等边三角形,
∴∠K=60°.KC=BC=AD=10,
∵∠HEP+∠HPE=120°,∠HPE+∠CPK=180°﹣60°=120°,
∴∠HEP=∠CPK,
又∠K=∠H=60°,PE=PC,
∴△EHP≌△PKC(AAS).
∴HP=KC=AD=HG=10,
∴△PGH 为等边三角形.
∵点M、N为PF、GF的中点,
∴MN为△PGF的中位线,MNPG.
∴PG=HG=AD=10.
∴MN=5.且长度不变;
连接CE,
由△CPE和△GPH都为等边三角形.
由手拉手模型易证△HPE≌△GPC(SAS).
∴CG=HE=AF.
设PG与 AD 交于I点,易证△API和△GDI为等边三角形.
由上可知:△API和△IGD为等边三角形,
∴GD=ID.
∴AF﹣DI=CG﹣DG,
∴AI+DF=DC=6=AP+PB,
∵AP=AI,
∴PB=DF,设AP=a,
则PB=6﹣a=DF,AI=AP=a,ID=10﹣a,
∴IF=ID+DF=10﹣a+6﹣a=16﹣2a.
∵MN为△GFP的中位线,Q为IF中点,
∴IQIF=8﹣a,
∴AQ=AI+IQ=a+8﹣a=8.
故MN和AQ的长度都不变.
6.【解答】解:(1)四边形AFHE是正方形,理由如下:
∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF,
∴∠AEB=∠AFD=90°,
∴∠AFH=90°,
在四边形AFHE中,∠FAE=90°,∠AEB=90°,∠AFH=90°,
∴四边形AFHE是矩形,
又∵AE=AF,
∴矩形AFHE是正方形;
(2)设AE=x.则由(1)以及题意可知:AE=EH=FH=AF=x,BH=7,BC=AB=13,
在Rt△AEB中,AB2=AE2+BE2,
即132=x2+(x+7)2,
解得:x=5(负值舍去),
∴BE=BH+EH=5+7=12,
∴DF=BE=12,
又∵DH=DF+FH,
∴DH=12+5=17.
7.【解答】(1)证明:∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,
∴AC=BD,
∴平行四边形ABCD是矩形,
∵OA=OB=OC=ODAB,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形;
(2)解:∵EF⊥BC,EG⊥AG,
∴∠G=∠EFB=∠FBG=90°,
∴四边形BGEF是矩形,
∵将线段DH绕点H顺时针旋转90°,得到线段HE,
∴∠DHE=90°,DH=HE,
∴∠ADH+∠AHD=∠AHD+∠EHG=90°,
∴∠ADH=∠EHG,
∵∠DAH=∠G=90°,
∴△ADH≌△GHE(AAS),
∴AD=HG,AH=EG,
∵AB=AD,
∴AB=HG,
∴AH=BG,
∴BG=EG,
∴矩形BGEF是正方形,
设AH=x,则BG=EG=x,
∵s1=s2.
∴x2=2(2﹣x),
解得:x1(负值舍去),
∴AH1.
8.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠ADC=90°.
∵∠EDF=45°,
∴∠EDA+∠CDF=45°.
由旋转得,DM=DE,∠MDC=∠EDA,
∴∠MDC+∠CDF=∠MDF=45°,
∴∠MDF=∠EDF.
∵DF=DF,
∴△DEF≌△DMF(SAS).
(2)解:∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC=4,
∴BE=AB﹣AE=3.
由旋转得,CM=AE=1,
∵△DEF≌△DMF,
∴EF=FM.
设EF=FM=x,则CF=FM﹣CM=x﹣1,
∴BF=BC﹣CF=4﹣(x﹣1)=5﹣x.
在Rt△BEF中,由勾股定理得,EF2=BF2+BE2,
即x2=(5﹣x)2+32,
解得x.
∴EF的长为.
9.【解答】(1)证明:如图,连接AC,AC′,
∵四边形ABCD为矩形,
∴∠ABC=90°,即AB⊥CC′,
∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,
∴AC=AC′,
∴BC′=BC;
(2)解:∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,
由旋转的性质得:BC′=BC=AD′,∠D′=∠EBC′=90°,
在△AED′和△C′EB中,
,
∴△AED′≌△C′EB(AAS),
∴AE=C′E,
设AE=x,则BE=3﹣x,BC′=1,
在直角三角形BC′E中,由勾股定理得:C′E2=C′B2+BE2,
∴(3﹣x)2+1=x2,
解得:,
∴.
10.【解答】(1)证明:∵四边形ABCD是正方形且△ABE是等边三角形,
∴AB=EB,
又由BM绕B点逆时针旋转60°得到BN,
则BM=BN,
又∵∠ABM+∠ABN=∠EBN+∠ABN=60°,
∴∠ABM=∠EBN,
在△AMB和△ENB中,
,
∴△AMB≌△ENB(SAS).
(2)连接CE,过E作CB延长线的垂线EF交于点F,
在Rt△EFB中,EB=2,∠EBF=180°﹣90°﹣60°=30°,
∴EF=1,
故△EBC的面积为.
11.【解答】解:(1)∵△CBD绕点B逆时针旋转90°至△ABE,
∴BE=BD=2,AE=CD=3,∠EBD=90°,
∴△EBD是等腰直角三角形,∠BDE=45°,
∴DE2,
∵AD2+DE2=1+8=9,
AE2=32=9,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,∠ADE=90°,
∠ADB=∠ADE+∠BDE=135°;
(2)延长DB交AC于点E,
∵AD=CD,BD=BD,AB=BC,
∴△ABD≌△CBD(SSS),
∴∠ADB=∠CDB,
∵AD=CD,DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,即E是AC中点,
∵∠ABC=90°,AB=BC,
∴△ABC是等腰直角三角形,
∴BE=AE=CE,BE⊥AC,
设BE为x,则AE=x,
∵AE2+DE2=AD2,
∴x2+(x)2=22,
解得:x,
∴BE,AC,DE,
过点A作AF⊥CD,交CD于点F,
设CF为y,则DF=(2﹣x),
在Rt△ACF中,AF,
在Rt△ADF中,AF,
∴,
解得:x=2,
∴DF,AF=1,
cos∠ADC,
∴∠ADC=30°,
∴∠ADB∠ADC=15°.
12.【解答】解:(1)由旋转的性质可知,∠DAE=60°,AD=AE,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,BD=CE,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°;
(2)如图,过点A作AM⊥BC于点M,
∵△ABC是等边三角形,
∴CMBCAB=3,
∴AM3,
∵CD=2,
∴DM=CM+CD=5,
∴AD2,
∵∠DAE=60°,AD=AE,
∴△ADE是等边三角形,
∴AD=DE,
∴DE=2.
13.【解答】解:(1)四边形BEGF是正方形.
由旋转可知,
∠F=∠AEB=90°,∠EBF=90°,EB=FB,
∴∠BEG=90°,
∴四边形BEGF是矩形.
又∵EB=FB,
∴四边形BEGF是正方形.
(2)过点D作AE的垂线,垂足为M,
∵∠DAM+∠EAB=∠DAM+∠ADM=90°,
∴∠EAB=∠ADM.
在△EAB和△MDA中,
,
∴△EAB≌△MDA(AAS),
∴AM=BE=2.
∵四边形BFGE是正方形,
∴FG=BE=2,
∴FC=2+1=3.
由旋转可知,
AE=FC=3,
∴DM=AE=3,ME=AE﹣AM=1.
在Rt△DME中,
DE.
所以DE的长为.
14.【解答】解:(1)以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交圆于M2,
∵△ACB是等腰直角三角形,N是AB中点,
∴CN平分∠ACB,CNAB4=2,
∵△DCE是等腰直角三角形,
∴M1是DE中点,
∴CM1DE2=1,
∴M、N距离的最小值是NM1=CN﹣CM1=2﹣1=1,M、N距离的最大值是NM2=CN+CM2=2+1=3.
(2)连接CM,CN,作NH⊥MC交MC延长线于H,
∵△ACB是等腰直角三角形,N是AB中点,
∴CNAB=2,
同理:CMDE=1,
∵△CDE绕顶点C逆时针旋转120°,
∴∠MCN=120°,
∴∠NCH=180°﹣∠MCN=60°,
∴CHCN=1,
∴NHCH,
∵MH=MC+CH=2,
∴MN.
15.【解答】解:(1)作C′H⊥DC于H,如图:
∵△ABC绕点A旋转到△AB'C',
∴AB'=AB=5,B'C'=BC=3,
∴DB'4,
∵∠C'B'H=90°﹣∠DB'A=∠DAB',∠CHB'=90°=∠D,
∴△C′HB′∽△B′DA,
∴即,
∴C'H,
∴,
∵S△AB'C'=S△B'C'M+S△AB'MAB' B'C',
∴S△AB'MS△AB'C';
∴△AB'C'与矩形ABCD重叠部分的面积是;
(2)作CN⊥AC',如图:
∵△ABC绕点A旋转到△AB'C',
∴AB'=AB=5,AC'=AC,∠AB'C'=∠B=90°=∠AB'C,B'C'=BC=3,
∴CC'=2B'C'=6,
∵2S△ACC'=CC' AB'=AC' CN,
∴CN,
∵∠CMN=∠AMD,∠CNM=∠ADM=90°,
∴△CMN∽△AMD,
∴,
∴,即CN2 AM2=AD2 CM2,
设DM=x,
∴()2×(x2+32)=32(x+5)2,
化简得:33x2﹣170x+25=0,
解得:x=5(舍去)或x,
答:DM的长度为.
方法二:(1)过M作MN⊥AB′于N,如图:
由旋转的性质可知,∠C′AB′=∠CAB,AB′=AB=5,
∴tan∠C′AB′=tan∠CAB,
在Rt△ADB′中,DB′4,
∴tan∠AB′D,
设MN=3x,则AN=5x,B′N=4x,
∴AB′=9x=5,
∴x,
∴MN,
∴S△AB′MMN AB′;
(2)设AB′交CD于N,如图:
由旋转的性质可知,AC′=AC,∠C′AB′=∠CAB,∠AB′C′=∠B=90°,
∴△ACC′为等腰三角形,∠C′AB′=CAB′,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠NAC=∠NCA,
∴AN=CN,
在Rt△ADN中,AD2+DN2=AN2,
即,9+DN2=(5﹣DN)2,
∴DN,
∵∠MNA=∠NAC+∠NCA,
∴∠MAC=∠MNA,
∵∠NMA=∠CMA,
∴△AMN∽△CAM,
∴,
∴AM2=MN CM,
在Rt△ADM中,AM2=MD2+AD2,
∴MN CM=MD2+AD2,
设DM=x,则MN=x,CM=5+x,
∴(x)(x+5)=x2+9,
解得:x,
即,DM.
21世纪教育网(www.21cnjy.com)
2025年九年级数学三轮冲刺训练图形的变换之旋转模型
1.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD.把AD绕点A逆时针旋转90°,得到AE,连接CE、DE.
(1)求证:△ABD≌△ACE;
(2)若,时,求BD的长.
2.如图,在正方形ABCD中,点E在边AB上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边BC的延长线上,连接DE,DF,EF.
(1)判断△DEF的形状,并证明;
(2)若,求△DEF的面积.
3.如图,将矩形ABCD绕点C顺时针旋转,得到矩形FGCE,使得点E落在边AB上,AB的延长线交EG于H,连接DE,DH.
(1)求证:ED平分∠AEC;
(2)求证:EC与DH互相平分.
4.如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
5.如图,在 ABCD中,AB=6,AD=10,∠BAD=60°,P为边AB上的动点.连接PC,将PC绕点P逆时针旋转60°得到PE,过点E作EF∥AB,EF交直线AD于点F.连接PF、DE,分别取PF、DE的中点M、N,连接MN,交AD于点Q.
(1)若点P与点B重合,则线段MN的长度为 .
(2)随着点P的运动,MN与AQ的长度是否发生变化?若不变,求出MN与AQ的长度;若改变,请说明理由.
6.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知BH=7,BC=13,求DH的长.
7.如图,四边形ABCD中,对角线AC与BD交于点O,且OA=OB=OC=ODAB.
(1)求证:四边形ABCD是正方形;
(2)若H是边AB上一点(H与A,B不重合),连接DH,将线段DH绕点H顺时针旋转90°,得到线段HE,过点E分别作BC及AB延长线的垂线,垂足分别为F,G.设四边形BGEF的面积为s1,以HB,BC为邻边的矩形的面积为s2,且s1=s2.当AB=2时,求AH的长.
8.正方形ABCD的边长为4,E、F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:△DEF≌△DMF;
(2)若AE=1,求EF的长.
9.如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
(1)求证:BC′=BC;
(2)若AB=3,BC=1,求AE的长.
10.如图,四边形ABCD是边长为2的正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕B点逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)若连接CE,求△EBC的面积.
11.在△ABC中,∠ABC=90°,AB=BC.
(1)如图1,若点D是△ABC内一点,DA=1,DB=2,DC=3.将△CBD绕点B逆时针旋转90°至△ABE,连接DE.判断△ADE的形状(要说明理由),并求∠ADB的度数;
(2)如图2,若点D是△ABC外一点,DA=2,,DC=2,求∠ADB的度数.
12.如图,等边△ABC,在BC边延长线上取点D,连接AD,将线段AD绕点D顺时针旋转60°得到线段DE,连接CE,AE.
(1)求∠ECD的度数;
(2)若AB=6,CD=2,求DE的长.
13.如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBF.延长AE交CF于点G,连接DE.
(1)试判断四边形BEGF的形状,并说明理由;
(2)若BE=2,CG=1,求DE.
14.如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
15.如图1,矩形ABCD中,AB=5,AD=3,将△ABC绕点A旋转到△AB'C'位置,设AC'交直线CD于点M.
(1)当点B'恰好落在DC边上时,求△AB'C'与矩形ABCD重叠部分的面积;
(2)如图2,当点C、B'、C'恰好在一直线上时,求DM的长度.
参考答案
1.【解答】(1)证明:由题意可得:AD=AE,∠DAE=90°,
∵∠BAC=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:设BD=x,
∵∠BAC=90°,,
∴∠ABD=∠ACD=45°,BC=4,
∵△ABD≌△ACE,
∴BD=CE=x,∠ABD=∠ACE=45°,
∴∠DCE=90°,
∴CD2+CE2=DE2,
∴,
解得x1=1,x2=3,
∴BD=1或3.
2.【解答】解:(1)△DEF是等腰直角三角形,
证明:在正方形ABCD中,DA=DC,∠ADC=∠DAB=∠DCB=90°,
∵F落在边BC的延长线上,
∴∠DCF=∠DAB=90°,
∵将点E绕点D逆时针旋转得到点F,
∴DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠ADE=∠CDF,
∵∠ADC=∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)∵△DEF是等腰直角三角形,
∴DE=DF,
∵,,
∴DE=DF=6,
∴△DEF的面积为.
3.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AED=∠EDC.
∵CE=CD,
∴∠CED=∠EDC,
∴∠AED=∠CED,
∴ED平分∠AEC.
(2)证明:连接HC,
∵四边形EFGC为矩形,
∴FG∥EC,
∴∠FHE=∠BEC.
∵∠F=∠EBC=90°,EF=CB,
在△EFH和△CBE中,
∴△EFH≌△CBE(AAS),
∴EH=EC.
结合EC=DC,知EH=DC.
则EH∥DC.
∴四边形EHCD为平行四边形,
∴EC与DH互相平分.
4.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC,∠ACD=45°,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB,
∴FH=CH=x,
∴CFFHx,
∴OE2﹣CF=x2x=(x)2,
∵点E在线段AO上(与端点不重合),
∴0<x,
∴当x时,OE2﹣CF的最小值是.
5.【解答】解:(1)当点P与点B重合时,点F在点D处,此时E、N、D、F、C共线,
如图①,在平行四边形ABCD中,BC=AD=10.
将PC绕点P逆时针旋转60°得到PE,PC=BC=PE=10.
点M、N分别是PF、ED的中点,由中位线可知2MN=PE=10.
∴MN=5.
故答案为:5.
(2)结论:不变.
如解图②,连接FN并延长到点G,使得FN=GN,连接 GE,DG,
∵点N为 DE中点,
∴EN=DN.
∴四边形GEFD 为平行四边形,
∴GE//AF,GD//EF.
延长EG,BA交于H点,连接PG.
∵GD//EF//HB,HG//AF.
∴四边形HADG为平行四边形,
∴HG=AD,
∴∠BAD=∠AHG=60°.
如解图②,延长AB至点K,使得BK=BC,连接CK,
在平行四边形ABCD中,
∵∠BAD=60°,
∴∠CBK=60°,
∴△BKC是等边三角形,
∴∠K=60°.KC=BC=AD=10,
∵∠HEP+∠HPE=120°,∠HPE+∠CPK=180°﹣60°=120°,
∴∠HEP=∠CPK,
又∠K=∠H=60°,PE=PC,
∴△EHP≌△PKC(AAS).
∴HP=KC=AD=HG=10,
∴△PGH 为等边三角形.
∵点M、N为PF、GF的中点,
∴MN为△PGF的中位线,MNPG.
∴PG=HG=AD=10.
∴MN=5.且长度不变;
连接CE,
由△CPE和△GPH都为等边三角形.
由手拉手模型易证△HPE≌△GPC(SAS).
∴CG=HE=AF.
设PG与 AD 交于I点,易证△API和△GDI为等边三角形.
由上可知:△API和△IGD为等边三角形,
∴GD=ID.
∴AF﹣DI=CG﹣DG,
∴AI+DF=DC=6=AP+PB,
∵AP=AI,
∴PB=DF,设AP=a,
则PB=6﹣a=DF,AI=AP=a,ID=10﹣a,
∴IF=ID+DF=10﹣a+6﹣a=16﹣2a.
∵MN为△GFP的中位线,Q为IF中点,
∴IQIF=8﹣a,
∴AQ=AI+IQ=a+8﹣a=8.
故MN和AQ的长度都不变.
6.【解答】解:(1)四边形AFHE是正方形,理由如下:
∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF,
∴∠AEB=∠AFD=90°,
∴∠AFH=90°,
在四边形AFHE中,∠FAE=90°,∠AEB=90°,∠AFH=90°,
∴四边形AFHE是矩形,
又∵AE=AF,
∴矩形AFHE是正方形;
(2)设AE=x.则由(1)以及题意可知:AE=EH=FH=AF=x,BH=7,BC=AB=13,
在Rt△AEB中,AB2=AE2+BE2,
即132=x2+(x+7)2,
解得:x=5(负值舍去),
∴BE=BH+EH=5+7=12,
∴DF=BE=12,
又∵DH=DF+FH,
∴DH=12+5=17.
7.【解答】(1)证明:∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,
∴AC=BD,
∴平行四边形ABCD是矩形,
∵OA=OB=OC=ODAB,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形;
(2)解:∵EF⊥BC,EG⊥AG,
∴∠G=∠EFB=∠FBG=90°,
∴四边形BGEF是矩形,
∵将线段DH绕点H顺时针旋转90°,得到线段HE,
∴∠DHE=90°,DH=HE,
∴∠ADH+∠AHD=∠AHD+∠EHG=90°,
∴∠ADH=∠EHG,
∵∠DAH=∠G=90°,
∴△ADH≌△GHE(AAS),
∴AD=HG,AH=EG,
∵AB=AD,
∴AB=HG,
∴AH=BG,
∴BG=EG,
∴矩形BGEF是正方形,
设AH=x,则BG=EG=x,
∵s1=s2.
∴x2=2(2﹣x),
解得:x1(负值舍去),
∴AH1.
8.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠ADC=90°.
∵∠EDF=45°,
∴∠EDA+∠CDF=45°.
由旋转得,DM=DE,∠MDC=∠EDA,
∴∠MDC+∠CDF=∠MDF=45°,
∴∠MDF=∠EDF.
∵DF=DF,
∴△DEF≌△DMF(SAS).
(2)解:∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC=4,
∴BE=AB﹣AE=3.
由旋转得,CM=AE=1,
∵△DEF≌△DMF,
∴EF=FM.
设EF=FM=x,则CF=FM﹣CM=x﹣1,
∴BF=BC﹣CF=4﹣(x﹣1)=5﹣x.
在Rt△BEF中,由勾股定理得,EF2=BF2+BE2,
即x2=(5﹣x)2+32,
解得x.
∴EF的长为.
9.【解答】(1)证明:如图,连接AC,AC′,
∵四边形ABCD为矩形,
∴∠ABC=90°,即AB⊥CC′,
∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,
∴AC=AC′,
∴BC′=BC;
(2)解:∵将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,
由旋转的性质得:BC′=BC=AD′,∠D′=∠EBC′=90°,
在△AED′和△C′EB中,
,
∴△AED′≌△C′EB(AAS),
∴AE=C′E,
设AE=x,则BE=3﹣x,BC′=1,
在直角三角形BC′E中,由勾股定理得:C′E2=C′B2+BE2,
∴(3﹣x)2+1=x2,
解得:,
∴.
10.【解答】(1)证明:∵四边形ABCD是正方形且△ABE是等边三角形,
∴AB=EB,
又由BM绕B点逆时针旋转60°得到BN,
则BM=BN,
又∵∠ABM+∠ABN=∠EBN+∠ABN=60°,
∴∠ABM=∠EBN,
在△AMB和△ENB中,
,
∴△AMB≌△ENB(SAS).
(2)连接CE,过E作CB延长线的垂线EF交于点F,
在Rt△EFB中,EB=2,∠EBF=180°﹣90°﹣60°=30°,
∴EF=1,
故△EBC的面积为.
11.【解答】解:(1)∵△CBD绕点B逆时针旋转90°至△ABE,
∴BE=BD=2,AE=CD=3,∠EBD=90°,
∴△EBD是等腰直角三角形,∠BDE=45°,
∴DE2,
∵AD2+DE2=1+8=9,
AE2=32=9,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,∠ADE=90°,
∠ADB=∠ADE+∠BDE=135°;
(2)延长DB交AC于点E,
∵AD=CD,BD=BD,AB=BC,
∴△ABD≌△CBD(SSS),
∴∠ADB=∠CDB,
∵AD=CD,DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,即E是AC中点,
∵∠ABC=90°,AB=BC,
∴△ABC是等腰直角三角形,
∴BE=AE=CE,BE⊥AC,
设BE为x,则AE=x,
∵AE2+DE2=AD2,
∴x2+(x)2=22,
解得:x,
∴BE,AC,DE,
过点A作AF⊥CD,交CD于点F,
设CF为y,则DF=(2﹣x),
在Rt△ACF中,AF,
在Rt△ADF中,AF,
∴,
解得:x=2,
∴DF,AF=1,
cos∠ADC,
∴∠ADC=30°,
∴∠ADB∠ADC=15°.
12.【解答】解:(1)由旋转的性质可知,∠DAE=60°,AD=AE,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,BD=CE,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°;
(2)如图,过点A作AM⊥BC于点M,
∵△ABC是等边三角形,
∴CMBCAB=3,
∴AM3,
∵CD=2,
∴DM=CM+CD=5,
∴AD2,
∵∠DAE=60°,AD=AE,
∴△ADE是等边三角形,
∴AD=DE,
∴DE=2.
13.【解答】解:(1)四边形BEGF是正方形.
由旋转可知,
∠F=∠AEB=90°,∠EBF=90°,EB=FB,
∴∠BEG=90°,
∴四边形BEGF是矩形.
又∵EB=FB,
∴四边形BEGF是正方形.
(2)过点D作AE的垂线,垂足为M,
∵∠DAM+∠EAB=∠DAM+∠ADM=90°,
∴∠EAB=∠ADM.
在△EAB和△MDA中,
,
∴△EAB≌△MDA(AAS),
∴AM=BE=2.
∵四边形BFGE是正方形,
∴FG=BE=2,
∴FC=2+1=3.
由旋转可知,
AE=FC=3,
∴DM=AE=3,ME=AE﹣AM=1.
在Rt△DME中,
DE.
所以DE的长为.
14.【解答】解:(1)以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交圆于M2,
∵△ACB是等腰直角三角形,N是AB中点,
∴CN平分∠ACB,CNAB4=2,
∵△DCE是等腰直角三角形,
∴M1是DE中点,
∴CM1DE2=1,
∴M、N距离的最小值是NM1=CN﹣CM1=2﹣1=1,M、N距离的最大值是NM2=CN+CM2=2+1=3.
(2)连接CM,CN,作NH⊥MC交MC延长线于H,
∵△ACB是等腰直角三角形,N是AB中点,
∴CNAB=2,
同理:CMDE=1,
∵△CDE绕顶点C逆时针旋转120°,
∴∠MCN=120°,
∴∠NCH=180°﹣∠MCN=60°,
∴CHCN=1,
∴NHCH,
∵MH=MC+CH=2,
∴MN.
15.【解答】解:(1)作C′H⊥DC于H,如图:
∵△ABC绕点A旋转到△AB'C',
∴AB'=AB=5,B'C'=BC=3,
∴DB'4,
∵∠C'B'H=90°﹣∠DB'A=∠DAB',∠CHB'=90°=∠D,
∴△C′HB′∽△B′DA,
∴即,
∴C'H,
∴,
∵S△AB'C'=S△B'C'M+S△AB'MAB' B'C',
∴S△AB'MS△AB'C';
∴△AB'C'与矩形ABCD重叠部分的面积是;
(2)作CN⊥AC',如图:
∵△ABC绕点A旋转到△AB'C',
∴AB'=AB=5,AC'=AC,∠AB'C'=∠B=90°=∠AB'C,B'C'=BC=3,
∴CC'=2B'C'=6,
∵2S△ACC'=CC' AB'=AC' CN,
∴CN,
∵∠CMN=∠AMD,∠CNM=∠ADM=90°,
∴△CMN∽△AMD,
∴,
∴,即CN2 AM2=AD2 CM2,
设DM=x,
∴()2×(x2+32)=32(x+5)2,
化简得:33x2﹣170x+25=0,
解得:x=5(舍去)或x,
答:DM的长度为.
方法二:(1)过M作MN⊥AB′于N,如图:
由旋转的性质可知,∠C′AB′=∠CAB,AB′=AB=5,
∴tan∠C′AB′=tan∠CAB,
在Rt△ADB′中,DB′4,
∴tan∠AB′D,
设MN=3x,则AN=5x,B′N=4x,
∴AB′=9x=5,
∴x,
∴MN,
∴S△AB′MMN AB′;
(2)设AB′交CD于N,如图:
由旋转的性质可知,AC′=AC,∠C′AB′=∠CAB,∠AB′C′=∠B=90°,
∴△ACC′为等腰三角形,∠C′AB′=CAB′,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠NAC=∠NCA,
∴AN=CN,
在Rt△ADN中,AD2+DN2=AN2,
即,9+DN2=(5﹣DN)2,
∴DN,
∵∠MNA=∠NAC+∠NCA,
∴∠MAC=∠MNA,
∵∠NMA=∠CMA,
∴△AMN∽△CAM,
∴,
∴AM2=MN CM,
在Rt△ADM中,AM2=MD2+AD2,
∴MN CM=MD2+AD2,
设DM=x,则MN=x,CM=5+x,
∴(x)(x+5)=x2+9,
解得:x,
即,DM.
21世纪教育网(www.21cnjy.com)
同课章节目录
