2025年九年级数学三轮冲刺训练相似三角形之一线三等角模型(含解析)
文档属性
| 名称 | 2025年九年级数学三轮冲刺训练相似三角形之一线三等角模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 829.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 07:28:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学三轮冲刺训练相似三角形之一线三等角模型
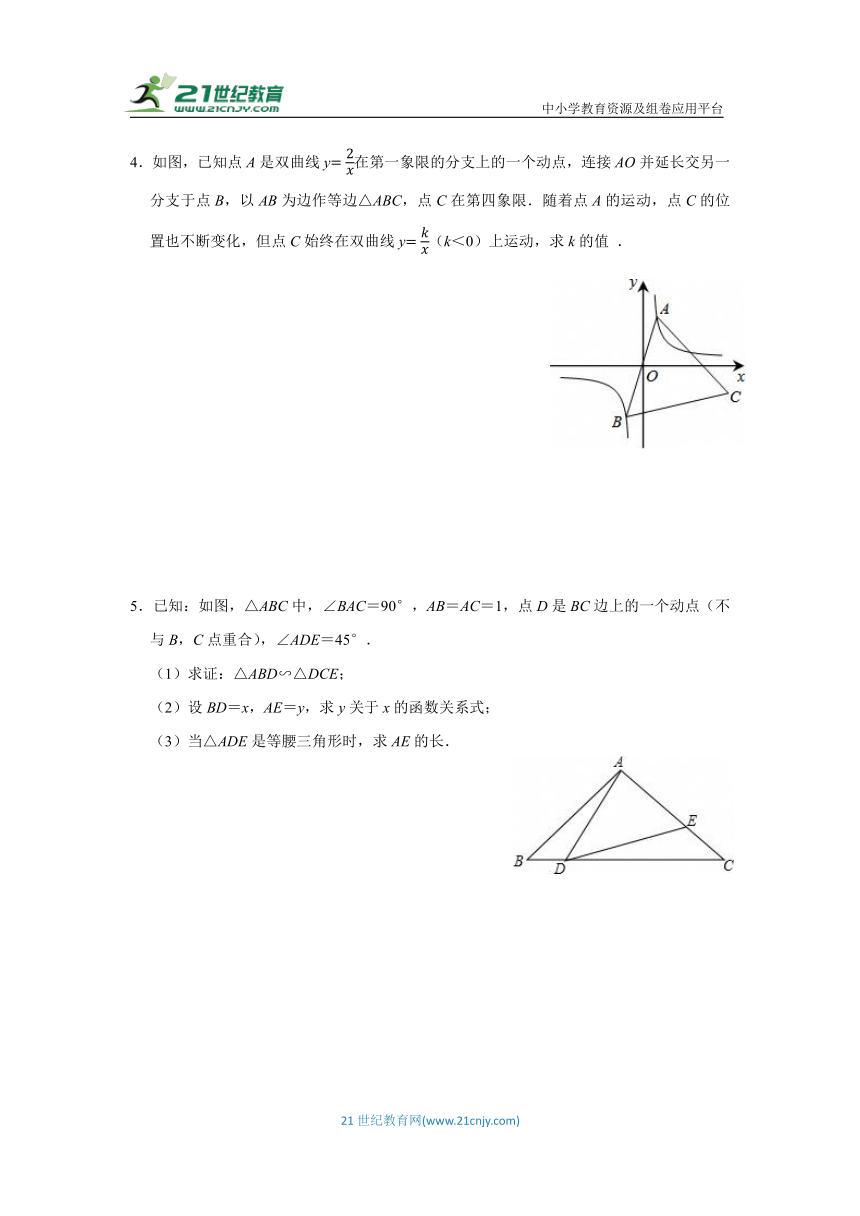
1.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象经过点A,反比例函数的图象经过点B,若n=﹣1,求m的值.
如图,点D,E是正△ABC两边上的点,将△BDE沿直线DE翻折,点B的对应点恰好落在边AC上,当AC=4AF时,求的值.
3.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,求△ABC的边长 .
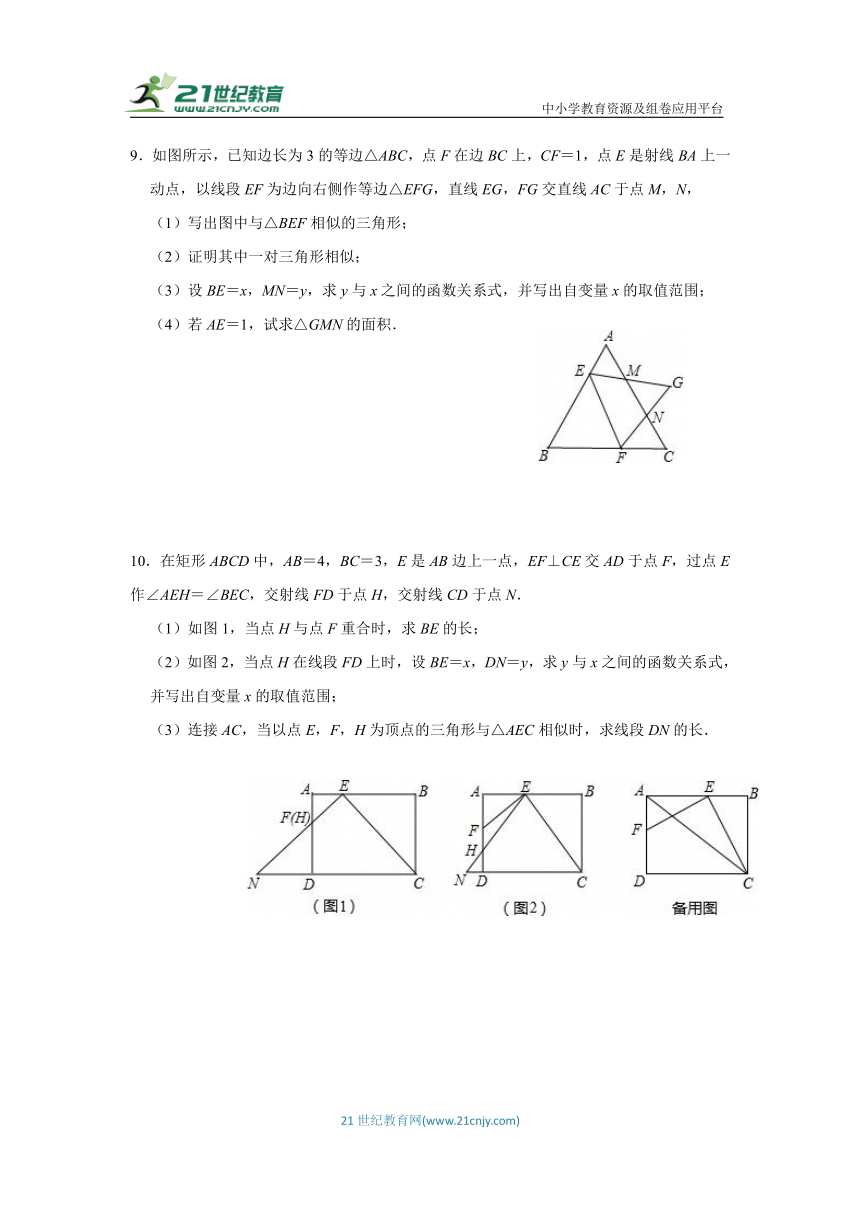
4.如图,已知点A是双曲线y在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y(k<0)上运动,求k的值 .
5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
6.如图,等边三角形ABC的边长为6,D是BC上一动点,∠EDF=60°.
(1)求证:△BDE∽△CFD.
(2)当BD=1,FC=3时,求BE的长.
7.已知矩形ABCD中,CD=2,P是射线DA上的一个动点,(和A、D不重合)过点P作PE⊥CP,交射线BA于点E.
(1)如图1,当AD=5时,点P在边AD上时,求证:△APE∽△DCP;
(2)如图1,当AD=5时,点P在边AD上时,设PD=x,AE=y,求y与x的函数关系式,并写出x的取值范围.
(3)如图2,当AD=3时,联结CE,当△PCE是等腰三角形时,求PD的长度.
8.如图,在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,E是在AC边上的一个动点(与点A、C不重合),DF⊥DE,DF与射线BC相交于点F.
(1)如图2,如果点D是边AB的中点,求证:DE=DF;
(2)如果AD:DB=m,求DE:DF的值;
(3)如果AC=BC=6,AD:DB=1:2,设AE=x,BF=y,
①求y关于x的函数关系式,并写出定义域;
②以CE为直径的圆与直线AB是否可相切?若可能,求出此时x的值;若不可能,请说明理由.
9.如图所示,已知边长为3的等边△ABC,点F在边BC上,CF=1,点E是射线BA上一动点,以线段EF为边向右侧作等边△EFG,直线EG,FG交直线AC于点M,N,
(1)写出图中与△BEF相似的三角形;
(2)证明其中一对三角形相似;
(3)设BE=x,MN=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(4)若AE=1,试求△GMN的面积.
10.在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图1,当点H与点F重合时,求BE的长;
(2)如图2,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)连接AC,当以点E,F,H为顶点的三角形与△AEC相似时,求线段DN的长.
11.三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型).解决此模型问题的一般方法是利用三等角关系找全等或相似三角形所需角的相等条件,利用全等或相似三角形解决问题.
【证明体验】
(1)如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD BC=AP BP.
【思考探究】
(2)如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=β时,上述结论是否依然成立?说明理由.
【拓展延伸】
(3)请利用(1)(2)获得的经验解决问题:
如图3,在△ABC中,,∠B=45°,以点A为直角顶点作等腰Rt△ADE,点D在BC上,点E在AC上,点F在BC上,且∠EFD=45°,若,求CD的长.
12.如图,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD:AB=3:1,CE垂直y轴于点E.
(1)求证:△CDE∽△DAO;
(2)直接写出点B和点C的坐标.
13.如图,矩形ABCD中,E为DC上一点,把△ADE沿AE翻折,点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若,AD=12,求CE的长.
14.在△ABC中,∠BAC=120°,点D为BC的中点,点E、F分别在边AB、AC上.
(1)如图1,若AB=AC=6,DE⊥AB,DF⊥AC,求AE+AF的值;
(2)如图2,当∠EDF=60°,AB=AC时,求证:;
(3)如图3,连接EF,已知∠EDF=90°,∠AEF=55°,∠DEF=40°,若,用三条线段BE、EF、CF围成的三角形的面积为,求CF的长.
15.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
参考答案
1.解:过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N.
∵∠AOB=90°,
∴∠BON+∠AOM=90°.
∵∠AMO=∠BNO=90°,
∴∠AOM+∠OAM=90°,
∴∠BON=∠OAM,
∴△BON∽△OAM,
∴.
∵∠OAB=30°,
∴,
∴,即.
设ON=a,BN=b,则,,
∴B(﹣a,b),.
∵点B在反比例函数的图象上,且n=﹣1,
∴ab=1.
∵点A在反比例函数的图象上,
∴.
2.解:∵AC=4AF,
∴设AF=x,则AC=4x,CF=3x,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵将△BDE沿直线DE翻折,点B的对应点恰好落在边AC上,
∴∠DFE=∠B=60°,BD=DF,BE=EF,
∴∠AFD+∠ADF=∠AFD+∠CFE=120°,
∴∠ADF=∠CFE,
∴△ADF∽△CFE,
∴△ADF周长:△CEF周长,
故选:D.
3.解:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∴CD=BC﹣BD=AB﹣3,
∴∠BAD+∠ADB=120°,
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
∴,
即;
解得AB=9,
经检验AB=9是方程的根,
∴△ABC的边长为9.
故答案为:9.
4.解:∵双曲线y关于原点对称,
∴点A与点B关于原点对称.
∴OA=OB.
连接OC,如图所示.
∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°.
∴tan∠OAC.
∴OCOA.
过点A作AE⊥y轴,垂足为E,
过点C作CF⊥y轴,垂足为F,
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF.
∴△AEO∽△OFC.
∴.
∵OCOA,
∴OFAE,FCEO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OFAEa,FCEOb.
∵点A在双曲线y上,
∴ab=2.
∴FC OFb a=3ab=6
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FC OF=x (﹣y)=﹣xy
=6.
∴xy=﹣6.
∵点C在双曲线y上,
∴k=xy=﹣6.
5.【解答】(1)证明:
∵∠BAC=90°,AB=AC
∴∠B=∠C=∠ADE=45°
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)由(1)得△ABD∽△DCE,
∴,
∵∠BAC=90°,AB=AC=1,
∴BC,CDx,EC=1﹣y,
∴,
∴y=x2x+1=(x)2(0<x);
(3)当AD=DE时,△ABD≌△CDE,
∴BD=CE,
∴x=1﹣y,即 x﹣x2=x,
∵x≠0,
∴等式左右两边同时除以x得:x1
∴AE=1﹣x=2,
当AE=DE时,DE⊥AC,此时D是BC中点,E也是AC的中点,
所以,AE;
当AD=AE时,∠DAE=90°,D与B重合,不合题意;
综上,在AC上存在点E,使△ADE是等腰三角形,
AE的长为2或 .
6.【解答】(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF+∠CDF=∠B+∠BED,∠EDF=60°,
∴∠BED=∠CDF,
∴△BDE∽△CFD;
(2)解:在等边△ABC中,边长为6,BD=1,
∴CD=BC﹣BD=5,
∵△BDE∽△CFD,
∴BE:CD=BD:CF,
∴BE:5=1:3,
∴BE.
7.解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵PE⊥CP,
∴∠EPC=90°,
∴∠APE+∠CPD=90°,
∵∠APE+∠AEP=90°,
∴∠CPD=∠AEP,
∴△APE∽△DCP;
(2)∵AD=5,PD=x,
∴AP=5﹣x,
由(1)知:△APE∽△DCP,
∴,
∴
yx(0<x<5);
(3)当△PCE是等腰三角形时,存在两种情况:
①如图1,当P在边AD上时,EP=CP,则△APE≌△DCP,
∴AP=DC=2,
∵AD=3,
∴PD=3﹣2=1;
②如图2,当P在射线DA上时,EP=PC,则△AEP≌△DPC,
∴AP=CD=2,
∵AD=3,
∴PD=AP+AD=3+2=5,
综上,PD的长为1或5.
8.【解答】(1)证明:如图2,连接DC.
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵点D是AB中点,
∴∠BCD=∠ACD=45°,CD=BD,
∴∠ACD=∠B=45°.
∵ED⊥DF,CD⊥AB,
∴∠EDC+∠CDF=90°,∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
∴△CED≌△BFD(ASA),
∴DE=DF;
(2)解:如图1,作DP⊥AC,DQ⊥BC,垂足分别为点Q,P.
∵∠B=∠A,∠APD=∠BQD=90°,
∴△ADP∽△BDQ,
∴DP:DQ=AD:DB=m.
∵∠CPD=∠CQD=90°,∠C=90°,
∴∠QDP=90°,
∵DF⊥DE,∴∠EDF=90°,
∴∠QDF=∠PDE,
∵∠DQF=∠DPE=90°,
∴△DQF∽△DPE,
∴DE:DF=DP:DQ,
∴DE:DF=DP:DQ=AD:DB=m;
(3)解:①如备用图1,作EG⊥AB,FH⊥AB,垂足分别为点G、H.
在Rt△ABC中,∠C=90°,AC=BC=6,
∴AB,
∵AD:DB=1:2,
∴AD,DB.
由∠AGE=∠BHF=90°,∠A=∠B=45°,
可得AG=EG,BH=FH,
GD,HD,
易证△DGE∽△FHD,
∴,
∴,
∴y=8﹣2x,
定义域是0<x≤4.
②如备用图2,取CE的中点O,作OM⊥AB于M.
可得CE=6﹣x,AO,OM.
若以CE为直径的圆与直线AB相切,则,
解得,
∴当时,以CE为直径的圆与直线AB相切.
9.解:(1)△BEF∽△AME∽△CFN∽△GMN;(3分)
证明:(2)在△BEF与△AME中,
∵∠B=∠A=60°,
∴∠AEM+∠AME=120°,(1分)
∵∠GEF=60°,
∴∠AEM+∠BEF=120°,
∴∠BEF=∠AME,(1分)
∴△BEF∽△AME;(1分)
解:(3)(i)当点E在线段AB上,点M、N在线段AC上时,如图,
∵△BEF∽△AME,
∴BE:AM=BF:AE,
即:x:AM=2:(3﹣x),
∴AM,
同理可证△BEF∽△CFN;
∴BE:CF=BF:CN,
即:x:1=2:CN,
∴CN,
∵AC=AM+MN+CN,
∴3y,
∴y(1≤x≤3);
(ii)当点E在线段AB上,点G在△ABC内时,如备用图一,
同上可得:AM,CN,
∵AC=AM+CN﹣MN,
∴3y,
∴y(0<x≤1);
(iii)当点E在线段BA的延长线上时,如备用图二,
AM,CN,
∵AC=MN+CN﹣AM,
∴3=y,
∴y(x>3);
综上所述:y(0<x≤1),
或∴y(x≥1);
(4)(i)当AE=1时,△GMN是边长为1等边三角形,
∴S△GMN1;(1分)
(ii)当AE=1时,△GMN是有一个角为30°的Rt△,
∵x=4,
∴y,NG=FG﹣FN=41,
∴S△GMN.
10.解:(1)如图,∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠AEF=∠BEC,
∴∠BEC=45°,
∵∠B=90°,
∴BE=BC,
∵BC=3,
∴BE=3;
(2)如图,过点E作EG⊥CN,垂足为点G,
∴BE=CG,
∵AB∥CN,
∴∠AEH=∠N,∠BEC=∠ECN,
∵∠AEH=∠BEC,
∴∠N=∠ECN,
∴EN=EC,
∴CN=2CG=2BE,
∵BE=x,DN=y,CD=AB=4,
∴y=2x﹣4(2≤x≤3);
(3)如图,∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当以点E,F,H为顶点的三角形与△AEC相似时,
(ⅰ)若∠FHE=∠EAC时,
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴tan∠EAC=tan∠ECB,
∴,
∴BE,
∴DN;
(ⅱ)
如图,设EG与AC于点O,
∵EN=EC,EG⊥CN,
∴∠1=∠2,
∵AH∥EG,
∴∠FHE=∠1,
∴∠FHE=∠2,
∴∠2=∠ECA,
∴OE=OC,
设OE=OC=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k,
∴AE,BE,
∴DN=1,
综上所述,线段DN的长为或1.
11.【解答】(1)证明:∵∠DPC=∠A=∠B=90°,
∴∠APD+∠BPC=90°,∠ADP+∠APD=90°,
∴∠BPC=∠ADP,
∵∠A=∠B=90°,
∴△BPC∽△ADP,
∴,
∴AD BC=AP BP;
(2)解:成立,理由如下:
∵∠DPC=∠A=∠B=β,
∴∠DPC+∠BPC=∠ADP+∠A,
即∠BPC=∠ADP,
∵∠DPC=∠A=∠B=β,
∴△BPC∽△ADP,
∴,
∴AD BC=AP BP;
(3)解:∵Rt△ADE是等腰三角形,
∴,
∵∠B=45°,∠EFD=45°,
∴与(1)、(2)同理,得△ABD∽△DFE,
,
∵,
∴DF=4,
∵∠AED=45°,∠EFD=45°,
∴∠DEC=180°﹣45°=∠EFC,
∵∠C=∠C,
∴△DEC∽△EFC,
∴,
即,
解得FC=1,FC=﹣5(FC为线段,负值舍去),
∴CD=1+4=5.
12.【解答】(1)证明:∵四边形ABCD是矩形,
∴CD=AB,∠ADC=90°,
∴∠ADO+∠CDE=∠CDE+∠DCE=90°,
∴∠DCE=∠ADO,
∴△CDE∽△ADO.
(2)解:∵△CDE∽△DAO,
∴,
∵OD=2OA=6,AD:AB=3:1,
∴OA=3,CD:AD,
∴CEOD=2,DEOA=1,
∴OE=7,
∴C(2,7),
利用平移的性质可得B(5,1).
13.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∵△ADE沿AE翻折得到△AFE,
∴∠D=∠AFE=90°,
∵∠BAF+∠AFB=90°,∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
∴△ABF∽△FCE;
(2)解:∵,AD=12,
∴BC=AD=AF=12,
在Rt△ABF中,,
∴CF=BC﹣BF=12﹣6=6,
由(1)可得:△ABF∽△FCE,
∴,
即,
解得:,
故CE长为.
14.【解答】(1)解:连接AD,
∵点D为BC的中点,
∴BD=CD,
∵AB=AC=6,
∴AD⊥BC,∠BAD∠BAC=60°,
∴∠B=30°,
∴ADAB=3,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=30°,
∴AE,
同理,AF=1.5,
∴AE+AF=3;
(2)证明:如图1中,连接AD,作DM⊥AB于M,DN⊥AC于N.
∵AB=AC,BD=CD,
∴AD⊥BC,∠BAD=∠CAD∠BAC=60°,
∵DM⊥AB,DN⊥AC,
∴∠AMD=∠AND=90°,DM=DN,
∴∠MDN=60°,
∵∠EDF=60°,
∴∠MDN=∠EDF,
∴∠MDE=∠NDF,
∴△DME≌△DNF(ASA),Rt△DAM≌Rt△DAN(HL),
∴EM=FN,AM=AN,
∴AE+AF=AM﹣EM+AN+FN=2AM,
∵∠ADM=30°,∠AMD=90°,
∴AD=2AM,
∵∠ADC=90°,∠C=30°,
∴AC=2AD,
∴AE+AF=ADAC;
(3)解:延长ED到K,使得DK=DE,连接EK,CK,作FH⊥CK于H.
∵DE=DK,∠BDE=∠CDK,BD=DC,
∴△BDE≌△CDK(SAS),
∴BE=CK=6+2,∠B=∠DCK,
∵∠A=120°,
∴∠B+∠ACB=60°,
∴∠FCK=∠DCK+∠ACB=∠B+∠ACB=60°
∵∠EDF=90°,
∴FD⊥EK,
∵DE=DK,
∴FE=FK,
由题意得:S△CFK,
∵FH⊥CK,
∴(6+2)×FH=18+6,
∴FH=6,CH=2,
CF=2CH=4.
15.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
21世纪教育网(www.21cnjy.com)
2025年九年级数学三轮冲刺训练相似三角形之一线三等角模型
1.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象经过点A,反比例函数的图象经过点B,若n=﹣1,求m的值.
如图,点D,E是正△ABC两边上的点,将△BDE沿直线DE翻折,点B的对应点恰好落在边AC上,当AC=4AF时,求的值.
3.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,求△ABC的边长 .
4.如图,已知点A是双曲线y在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y(k<0)上运动,求k的值 .
5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
6.如图,等边三角形ABC的边长为6,D是BC上一动点,∠EDF=60°.
(1)求证:△BDE∽△CFD.
(2)当BD=1,FC=3时,求BE的长.
7.已知矩形ABCD中,CD=2,P是射线DA上的一个动点,(和A、D不重合)过点P作PE⊥CP,交射线BA于点E.
(1)如图1,当AD=5时,点P在边AD上时,求证:△APE∽△DCP;
(2)如图1,当AD=5时,点P在边AD上时,设PD=x,AE=y,求y与x的函数关系式,并写出x的取值范围.
(3)如图2,当AD=3时,联结CE,当△PCE是等腰三角形时,求PD的长度.
8.如图,在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,E是在AC边上的一个动点(与点A、C不重合),DF⊥DE,DF与射线BC相交于点F.
(1)如图2,如果点D是边AB的中点,求证:DE=DF;
(2)如果AD:DB=m,求DE:DF的值;
(3)如果AC=BC=6,AD:DB=1:2,设AE=x,BF=y,
①求y关于x的函数关系式,并写出定义域;
②以CE为直径的圆与直线AB是否可相切?若可能,求出此时x的值;若不可能,请说明理由.
9.如图所示,已知边长为3的等边△ABC,点F在边BC上,CF=1,点E是射线BA上一动点,以线段EF为边向右侧作等边△EFG,直线EG,FG交直线AC于点M,N,
(1)写出图中与△BEF相似的三角形;
(2)证明其中一对三角形相似;
(3)设BE=x,MN=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(4)若AE=1,试求△GMN的面积.
10.在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图1,当点H与点F重合时,求BE的长;
(2)如图2,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)连接AC,当以点E,F,H为顶点的三角形与△AEC相似时,求线段DN的长.
11.三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型).解决此模型问题的一般方法是利用三等角关系找全等或相似三角形所需角的相等条件,利用全等或相似三角形解决问题.
【证明体验】
(1)如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD BC=AP BP.
【思考探究】
(2)如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=β时,上述结论是否依然成立?说明理由.
【拓展延伸】
(3)请利用(1)(2)获得的经验解决问题:
如图3,在△ABC中,,∠B=45°,以点A为直角顶点作等腰Rt△ADE,点D在BC上,点E在AC上,点F在BC上,且∠EFD=45°,若,求CD的长.
12.如图,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD:AB=3:1,CE垂直y轴于点E.
(1)求证:△CDE∽△DAO;
(2)直接写出点B和点C的坐标.
13.如图,矩形ABCD中,E为DC上一点,把△ADE沿AE翻折,点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若,AD=12,求CE的长.
14.在△ABC中,∠BAC=120°,点D为BC的中点,点E、F分别在边AB、AC上.
(1)如图1,若AB=AC=6,DE⊥AB,DF⊥AC,求AE+AF的值;
(2)如图2,当∠EDF=60°,AB=AC时,求证:;
(3)如图3,连接EF,已知∠EDF=90°,∠AEF=55°,∠DEF=40°,若,用三条线段BE、EF、CF围成的三角形的面积为,求CF的长.
15.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
参考答案
1.解:过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N.
∵∠AOB=90°,
∴∠BON+∠AOM=90°.
∵∠AMO=∠BNO=90°,
∴∠AOM+∠OAM=90°,
∴∠BON=∠OAM,
∴△BON∽△OAM,
∴.
∵∠OAB=30°,
∴,
∴,即.
设ON=a,BN=b,则,,
∴B(﹣a,b),.
∵点B在反比例函数的图象上,且n=﹣1,
∴ab=1.
∵点A在反比例函数的图象上,
∴.
2.解:∵AC=4AF,
∴设AF=x,则AC=4x,CF=3x,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵将△BDE沿直线DE翻折,点B的对应点恰好落在边AC上,
∴∠DFE=∠B=60°,BD=DF,BE=EF,
∴∠AFD+∠ADF=∠AFD+∠CFE=120°,
∴∠ADF=∠CFE,
∴△ADF∽△CFE,
∴△ADF周长:△CEF周长,
故选:D.
3.解:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∴CD=BC﹣BD=AB﹣3,
∴∠BAD+∠ADB=120°,
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
∴,
即;
解得AB=9,
经检验AB=9是方程的根,
∴△ABC的边长为9.
故答案为:9.
4.解:∵双曲线y关于原点对称,
∴点A与点B关于原点对称.
∴OA=OB.
连接OC,如图所示.
∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°.
∴tan∠OAC.
∴OCOA.
过点A作AE⊥y轴,垂足为E,
过点C作CF⊥y轴,垂足为F,
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF.
∴△AEO∽△OFC.
∴.
∵OCOA,
∴OFAE,FCEO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OFAEa,FCEOb.
∵点A在双曲线y上,
∴ab=2.
∴FC OFb a=3ab=6
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FC OF=x (﹣y)=﹣xy
=6.
∴xy=﹣6.
∵点C在双曲线y上,
∴k=xy=﹣6.
5.【解答】(1)证明:
∵∠BAC=90°,AB=AC
∴∠B=∠C=∠ADE=45°
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)由(1)得△ABD∽△DCE,
∴,
∵∠BAC=90°,AB=AC=1,
∴BC,CDx,EC=1﹣y,
∴,
∴y=x2x+1=(x)2(0<x);
(3)当AD=DE时,△ABD≌△CDE,
∴BD=CE,
∴x=1﹣y,即 x﹣x2=x,
∵x≠0,
∴等式左右两边同时除以x得:x1
∴AE=1﹣x=2,
当AE=DE时,DE⊥AC,此时D是BC中点,E也是AC的中点,
所以,AE;
当AD=AE时,∠DAE=90°,D与B重合,不合题意;
综上,在AC上存在点E,使△ADE是等腰三角形,
AE的长为2或 .
6.【解答】(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF+∠CDF=∠B+∠BED,∠EDF=60°,
∴∠BED=∠CDF,
∴△BDE∽△CFD;
(2)解:在等边△ABC中,边长为6,BD=1,
∴CD=BC﹣BD=5,
∵△BDE∽△CFD,
∴BE:CD=BD:CF,
∴BE:5=1:3,
∴BE.
7.解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∵PE⊥CP,
∴∠EPC=90°,
∴∠APE+∠CPD=90°,
∵∠APE+∠AEP=90°,
∴∠CPD=∠AEP,
∴△APE∽△DCP;
(2)∵AD=5,PD=x,
∴AP=5﹣x,
由(1)知:△APE∽△DCP,
∴,
∴
yx(0<x<5);
(3)当△PCE是等腰三角形时,存在两种情况:
①如图1,当P在边AD上时,EP=CP,则△APE≌△DCP,
∴AP=DC=2,
∵AD=3,
∴PD=3﹣2=1;
②如图2,当P在射线DA上时,EP=PC,则△AEP≌△DPC,
∴AP=CD=2,
∵AD=3,
∴PD=AP+AD=3+2=5,
综上,PD的长为1或5.
8.【解答】(1)证明:如图2,连接DC.
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵点D是AB中点,
∴∠BCD=∠ACD=45°,CD=BD,
∴∠ACD=∠B=45°.
∵ED⊥DF,CD⊥AB,
∴∠EDC+∠CDF=90°,∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
∴△CED≌△BFD(ASA),
∴DE=DF;
(2)解:如图1,作DP⊥AC,DQ⊥BC,垂足分别为点Q,P.
∵∠B=∠A,∠APD=∠BQD=90°,
∴△ADP∽△BDQ,
∴DP:DQ=AD:DB=m.
∵∠CPD=∠CQD=90°,∠C=90°,
∴∠QDP=90°,
∵DF⊥DE,∴∠EDF=90°,
∴∠QDF=∠PDE,
∵∠DQF=∠DPE=90°,
∴△DQF∽△DPE,
∴DE:DF=DP:DQ,
∴DE:DF=DP:DQ=AD:DB=m;
(3)解:①如备用图1,作EG⊥AB,FH⊥AB,垂足分别为点G、H.
在Rt△ABC中,∠C=90°,AC=BC=6,
∴AB,
∵AD:DB=1:2,
∴AD,DB.
由∠AGE=∠BHF=90°,∠A=∠B=45°,
可得AG=EG,BH=FH,
GD,HD,
易证△DGE∽△FHD,
∴,
∴,
∴y=8﹣2x,
定义域是0<x≤4.
②如备用图2,取CE的中点O,作OM⊥AB于M.
可得CE=6﹣x,AO,OM.
若以CE为直径的圆与直线AB相切,则,
解得,
∴当时,以CE为直径的圆与直线AB相切.
9.解:(1)△BEF∽△AME∽△CFN∽△GMN;(3分)
证明:(2)在△BEF与△AME中,
∵∠B=∠A=60°,
∴∠AEM+∠AME=120°,(1分)
∵∠GEF=60°,
∴∠AEM+∠BEF=120°,
∴∠BEF=∠AME,(1分)
∴△BEF∽△AME;(1分)
解:(3)(i)当点E在线段AB上,点M、N在线段AC上时,如图,
∵△BEF∽△AME,
∴BE:AM=BF:AE,
即:x:AM=2:(3﹣x),
∴AM,
同理可证△BEF∽△CFN;
∴BE:CF=BF:CN,
即:x:1=2:CN,
∴CN,
∵AC=AM+MN+CN,
∴3y,
∴y(1≤x≤3);
(ii)当点E在线段AB上,点G在△ABC内时,如备用图一,
同上可得:AM,CN,
∵AC=AM+CN﹣MN,
∴3y,
∴y(0<x≤1);
(iii)当点E在线段BA的延长线上时,如备用图二,
AM,CN,
∵AC=MN+CN﹣AM,
∴3=y,
∴y(x>3);
综上所述:y(0<x≤1),
或∴y(x≥1);
(4)(i)当AE=1时,△GMN是边长为1等边三角形,
∴S△GMN1;(1分)
(ii)当AE=1时,△GMN是有一个角为30°的Rt△,
∵x=4,
∴y,NG=FG﹣FN=41,
∴S△GMN.
10.解:(1)如图,∵EF⊥EC,
∴∠AEF+∠BEC=90°,
∵∠AEF=∠BEC,
∴∠BEC=45°,
∵∠B=90°,
∴BE=BC,
∵BC=3,
∴BE=3;
(2)如图,过点E作EG⊥CN,垂足为点G,
∴BE=CG,
∵AB∥CN,
∴∠AEH=∠N,∠BEC=∠ECN,
∵∠AEH=∠BEC,
∴∠N=∠ECN,
∴EN=EC,
∴CN=2CG=2BE,
∵BE=x,DN=y,CD=AB=4,
∴y=2x﹣4(2≤x≤3);
(3)如图,∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当以点E,F,H为顶点的三角形与△AEC相似时,
(ⅰ)若∠FHE=∠EAC时,
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴tan∠EAC=tan∠ECB,
∴,
∴BE,
∴DN;
(ⅱ)
如图,设EG与AC于点O,
∵EN=EC,EG⊥CN,
∴∠1=∠2,
∵AH∥EG,
∴∠FHE=∠1,
∴∠FHE=∠2,
∴∠2=∠ECA,
∴OE=OC,
设OE=OC=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k,
∴AE,BE,
∴DN=1,
综上所述,线段DN的长为或1.
11.【解答】(1)证明:∵∠DPC=∠A=∠B=90°,
∴∠APD+∠BPC=90°,∠ADP+∠APD=90°,
∴∠BPC=∠ADP,
∵∠A=∠B=90°,
∴△BPC∽△ADP,
∴,
∴AD BC=AP BP;
(2)解:成立,理由如下:
∵∠DPC=∠A=∠B=β,
∴∠DPC+∠BPC=∠ADP+∠A,
即∠BPC=∠ADP,
∵∠DPC=∠A=∠B=β,
∴△BPC∽△ADP,
∴,
∴AD BC=AP BP;
(3)解:∵Rt△ADE是等腰三角形,
∴,
∵∠B=45°,∠EFD=45°,
∴与(1)、(2)同理,得△ABD∽△DFE,
,
∵,
∴DF=4,
∵∠AED=45°,∠EFD=45°,
∴∠DEC=180°﹣45°=∠EFC,
∵∠C=∠C,
∴△DEC∽△EFC,
∴,
即,
解得FC=1,FC=﹣5(FC为线段,负值舍去),
∴CD=1+4=5.
12.【解答】(1)证明:∵四边形ABCD是矩形,
∴CD=AB,∠ADC=90°,
∴∠ADO+∠CDE=∠CDE+∠DCE=90°,
∴∠DCE=∠ADO,
∴△CDE∽△ADO.
(2)解:∵△CDE∽△DAO,
∴,
∵OD=2OA=6,AD:AB=3:1,
∴OA=3,CD:AD,
∴CEOD=2,DEOA=1,
∴OE=7,
∴C(2,7),
利用平移的性质可得B(5,1).
13.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∵△ADE沿AE翻折得到△AFE,
∴∠D=∠AFE=90°,
∵∠BAF+∠AFB=90°,∠EFC+∠AFB=90°,
∴∠BAF=∠EFC,
∴△ABF∽△FCE;
(2)解:∵,AD=12,
∴BC=AD=AF=12,
在Rt△ABF中,,
∴CF=BC﹣BF=12﹣6=6,
由(1)可得:△ABF∽△FCE,
∴,
即,
解得:,
故CE长为.
14.【解答】(1)解:连接AD,
∵点D为BC的中点,
∴BD=CD,
∵AB=AC=6,
∴AD⊥BC,∠BAD∠BAC=60°,
∴∠B=30°,
∴ADAB=3,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=30°,
∴AE,
同理,AF=1.5,
∴AE+AF=3;
(2)证明:如图1中,连接AD,作DM⊥AB于M,DN⊥AC于N.
∵AB=AC,BD=CD,
∴AD⊥BC,∠BAD=∠CAD∠BAC=60°,
∵DM⊥AB,DN⊥AC,
∴∠AMD=∠AND=90°,DM=DN,
∴∠MDN=60°,
∵∠EDF=60°,
∴∠MDN=∠EDF,
∴∠MDE=∠NDF,
∴△DME≌△DNF(ASA),Rt△DAM≌Rt△DAN(HL),
∴EM=FN,AM=AN,
∴AE+AF=AM﹣EM+AN+FN=2AM,
∵∠ADM=30°,∠AMD=90°,
∴AD=2AM,
∵∠ADC=90°,∠C=30°,
∴AC=2AD,
∴AE+AF=ADAC;
(3)解:延长ED到K,使得DK=DE,连接EK,CK,作FH⊥CK于H.
∵DE=DK,∠BDE=∠CDK,BD=DC,
∴△BDE≌△CDK(SAS),
∴BE=CK=6+2,∠B=∠DCK,
∵∠A=120°,
∴∠B+∠ACB=60°,
∴∠FCK=∠DCK+∠ACB=∠B+∠ACB=60°
∵∠EDF=90°,
∴FD⊥EK,
∵DE=DK,
∴FE=FK,
由题意得:S△CFK,
∵FH⊥CK,
∴(6+2)×FH=18+6,
∴FH=6,CH=2,
CF=2CH=4.
15.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
21世纪教育网(www.21cnjy.com)
同课章节目录
