函数y=Asin(ωx φ)的图象 学案
文档属性
| 名称 | 函数y=Asin(ωx φ)的图象 学案 |  | |
| 格式 | docx | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 13:58:02 | ||
图片预览

文档简介
函数的图象
【学习目标】
1.通过初中的平移经验得到函数图象并与的图象进行对比,从而归纳出对函数的图象的影响,体会由特殊到一般的化归思想。
2.完成探究三和探究四分别得到、对函数图象变化的影响,提高对五点法作图的认识和应用,体会方程思想并提升画图能力,发展直观想象和数学抽象素养。
3.合作探究完成探究五,分组展示讨论结果,并能从变换角度叙述图象的变换过程,进一步体会由简单到复杂,数形结合的数学思想。
【评价任务】
1.完成探究1,达成目标1;
2.完成探究2-4,达成目标2;
3.完成探究5和例题,达成目标3.
【资源与建议】
1.本节课首先复习了利用五点法画正弦曲线图象的五点坐标,为学生学习利用五点法画的图象奠定了基础,也为学生探索图象的变换规律提供了方法;
2.本节课的重点是图象的变换规律;难点是探索 对图象的影响;本节课将按照以下流程进行:情境引入 探究对的图象的影响 探究对的图象的影响 探究对的图象的影响 探究由到的图象变换 小结与反思。
3.本节课的作业布置内容比较新颖,除了常规试题(作业1),还有3道发挥学生创新思维能力的试题(作业2,3,4),对学生的综合能力要求较高,进一步体会数形结合、由特殊到一般的思想方法.
【学习过程】
【温故知新】
1.请大家回忆一下,作函数的图象,主要有哪些方法?
2.用五点法作出的图象时,五点的坐标是什么?
【合作探究】
一、探索研究的路径
探究1:从解析式看,函数就是函数在A=1,ω=1,φ=0时的特殊情形.
(1)我们可以借助熟悉的函数的图象与性质研究参数A,ω,φ对函数y=Asin(ωx+φ)的影响.
(2)函数 y=Asin(ωx+φ) 中含有三个参数,你认为应按怎样的思路进行研究?
二、探索用变换法作的图象
探究2.探索 对图象的影响
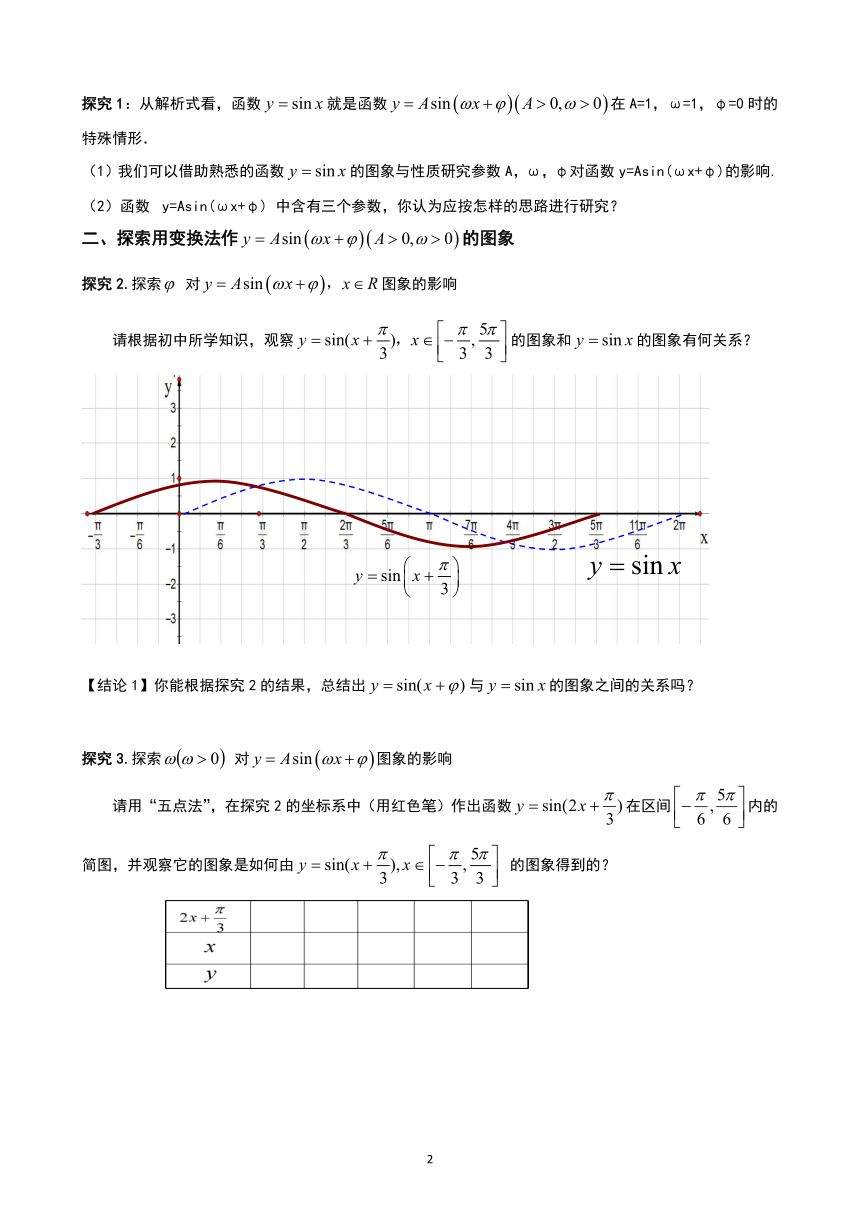
请根据初中所学知识,观察的图象和的图象有何关系?
【结论1】你能根据探究2的结果,总结出与的图象之间的关系吗?
探究3.探索 对图象的影响
请用“五点法”,在探究2的坐标系中(用红色笔)作出函数在区间内的简图,并观察它的图象是如何由 的图象得到的?
【结论2】你能根据探究3的结果,总结出与的图象之间的关系吗?
探究4.探索 对图象的影响
(不作图,对比探究3)思考的图象是如何由的图象得到的?
参考数据:
【结论3】你能根据探究4的结果,总结出与的图象之间的关系吗?
探究5.请结合下图,根据探究2~4的结论,小组讨论,函数的图象是如何由的图象得到的?
例1 画出函数的简图
【课堂小结】
1.知识点:
2.数学思想方法:
【检测任务】
1.已知函数的图象为C.
(1)为了得到函数的图象,只要把C上所有的点( )
A.向右平行移动个单位长度 B.向左平行移动个单位长度
C.向右平行移动个单位长度 D.向左平行移动个单位长度
(2)为了得到函数的图象,只要把C上所有的点( )
A.横坐标伸长到原来的2倍,纵坐标不变 B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的2倍,横坐标不变 D.纵坐标缩短到原来的倍,横坐标不变
(3)为了得到函数的图象,只要把C上所有的点( )
A.横坐标伸长到原来的倍,纵坐标不变 B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的倍,横坐标不变 D.纵坐标缩短到原来的倍,横坐标不变
2.为了得到函数的图象,只需将的图象上所有点向 平移 个单位长度.
3.思考:由经过怎样的变换得到的图象
4.思考:由经过怎样的变换得到的图象
【学后反思】请自主梳理本节课知识体系,你是通过什么方法和策略学会本节课内容的。你觉得还有什么地方比较薄弱,需要老师提供何种帮助,你还有什么好的经验可以跟大家分享。你可以选择其中的一点或几点写下来。
【学习目标】
1.通过初中的平移经验得到函数图象并与的图象进行对比,从而归纳出对函数的图象的影响,体会由特殊到一般的化归思想。
2.完成探究三和探究四分别得到、对函数图象变化的影响,提高对五点法作图的认识和应用,体会方程思想并提升画图能力,发展直观想象和数学抽象素养。
3.合作探究完成探究五,分组展示讨论结果,并能从变换角度叙述图象的变换过程,进一步体会由简单到复杂,数形结合的数学思想。
【评价任务】
1.完成探究1,达成目标1;
2.完成探究2-4,达成目标2;
3.完成探究5和例题,达成目标3.
【资源与建议】
1.本节课首先复习了利用五点法画正弦曲线图象的五点坐标,为学生学习利用五点法画的图象奠定了基础,也为学生探索图象的变换规律提供了方法;
2.本节课的重点是图象的变换规律;难点是探索 对图象的影响;本节课将按照以下流程进行:情境引入 探究对的图象的影响 探究对的图象的影响 探究对的图象的影响 探究由到的图象变换 小结与反思。
3.本节课的作业布置内容比较新颖,除了常规试题(作业1),还有3道发挥学生创新思维能力的试题(作业2,3,4),对学生的综合能力要求较高,进一步体会数形结合、由特殊到一般的思想方法.
【学习过程】
【温故知新】
1.请大家回忆一下,作函数的图象,主要有哪些方法?
2.用五点法作出的图象时,五点的坐标是什么?
【合作探究】
一、探索研究的路径
探究1:从解析式看,函数就是函数在A=1,ω=1,φ=0时的特殊情形.
(1)我们可以借助熟悉的函数的图象与性质研究参数A,ω,φ对函数y=Asin(ωx+φ)的影响.
(2)函数 y=Asin(ωx+φ) 中含有三个参数,你认为应按怎样的思路进行研究?
二、探索用变换法作的图象
探究2.探索 对图象的影响
请根据初中所学知识,观察的图象和的图象有何关系?
【结论1】你能根据探究2的结果,总结出与的图象之间的关系吗?
探究3.探索 对图象的影响
请用“五点法”,在探究2的坐标系中(用红色笔)作出函数在区间内的简图,并观察它的图象是如何由 的图象得到的?
【结论2】你能根据探究3的结果,总结出与的图象之间的关系吗?
探究4.探索 对图象的影响
(不作图,对比探究3)思考的图象是如何由的图象得到的?
参考数据:
【结论3】你能根据探究4的结果,总结出与的图象之间的关系吗?
探究5.请结合下图,根据探究2~4的结论,小组讨论,函数的图象是如何由的图象得到的?
例1 画出函数的简图
【课堂小结】
1.知识点:
2.数学思想方法:
【检测任务】
1.已知函数的图象为C.
(1)为了得到函数的图象,只要把C上所有的点( )
A.向右平行移动个单位长度 B.向左平行移动个单位长度
C.向右平行移动个单位长度 D.向左平行移动个单位长度
(2)为了得到函数的图象,只要把C上所有的点( )
A.横坐标伸长到原来的2倍,纵坐标不变 B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的2倍,横坐标不变 D.纵坐标缩短到原来的倍,横坐标不变
(3)为了得到函数的图象,只要把C上所有的点( )
A.横坐标伸长到原来的倍,纵坐标不变 B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的倍,横坐标不变 D.纵坐标缩短到原来的倍,横坐标不变
2.为了得到函数的图象,只需将的图象上所有点向 平移 个单位长度.
3.思考:由经过怎样的变换得到的图象
4.思考:由经过怎样的变换得到的图象
【学后反思】请自主梳理本节课知识体系,你是通过什么方法和策略学会本节课内容的。你觉得还有什么地方比较薄弱,需要老师提供何种帮助,你还有什么好的经验可以跟大家分享。你可以选择其中的一点或几点写下来。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
