初中数学沪教版(五四学制)(2024)七年级下册 17.4 三角形全等的判定 (含答案)
文档属性
| 名称 | 初中数学沪教版(五四学制)(2024)七年级下册 17.4 三角形全等的判定 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 882.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 11:17:09 | ||
图片预览


文档简介
17.4三角形全等的判定
一、单选题
1.如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
2.如图,和中,,,若,则等于( )
A.10° B.20° C.30° D.40°
3.如图,已知平分,那么就可以证明,理由是( )
A. B. C. D.
4.如图,已知,则的理由是( )
A. B. C. D.
5.如图,这是一个平分角的仪器,,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证,从而得到AC就是这个角的平分线.其中证明的数学依据是( )
A.SSS B.ASA C.SAS D.AAS
6.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是( )
A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B
7.作∠AOB的角平分线的作图过程如下:
用下面的三角形全等判定方法解释其作图原理,最为恰当的是( )
A.边角边 B.角边角 C.角角边 D.边边边
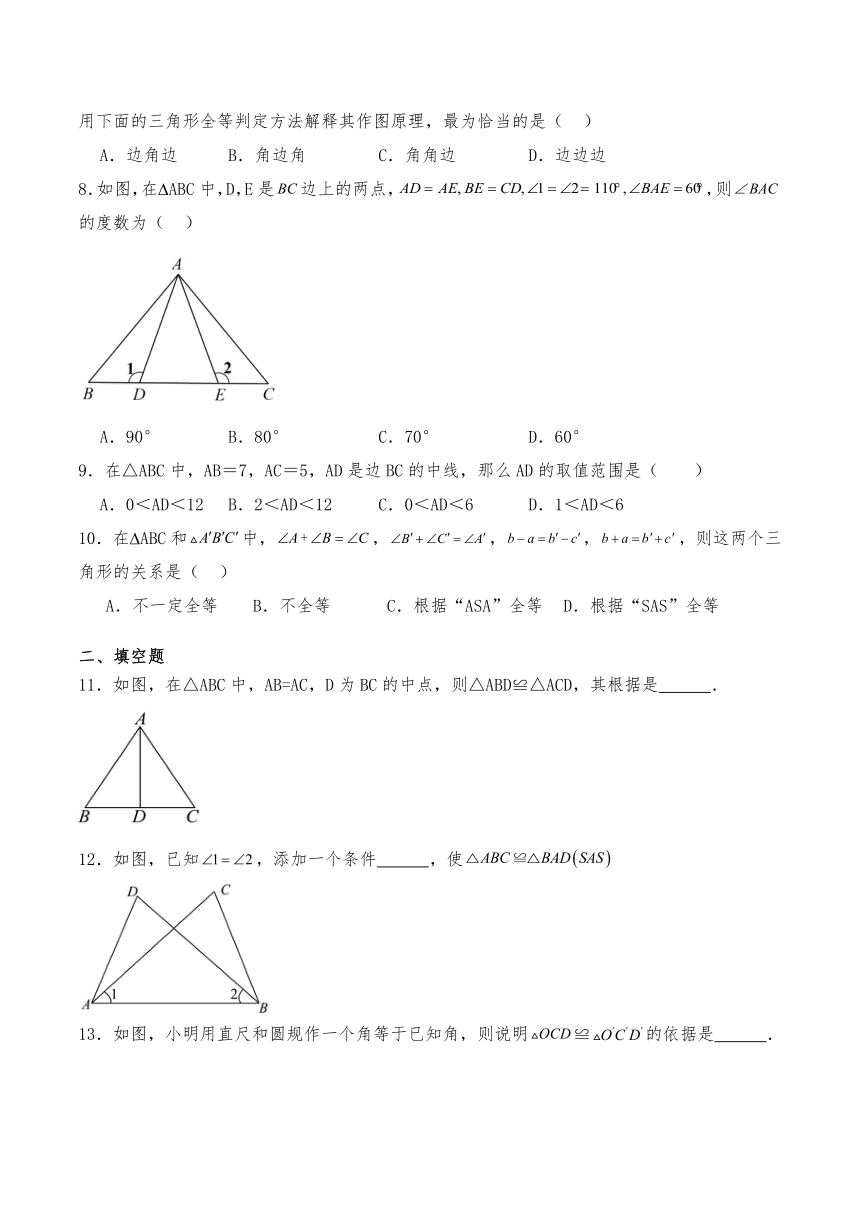
8.如图,在 ABC中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
9.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
10.在 ABC和中,,,,,则这两个三角形的关系是( )
A.不一定全等 B.不全等 C.根据“ASA”全等 D.根据“SAS”全等
二、填空题
11.如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是 .
12.如图,已知,添加一个条件 ,使
13.如图,小明用直尺和圆规作一个角等于已知角,则说明≌的依据是 .
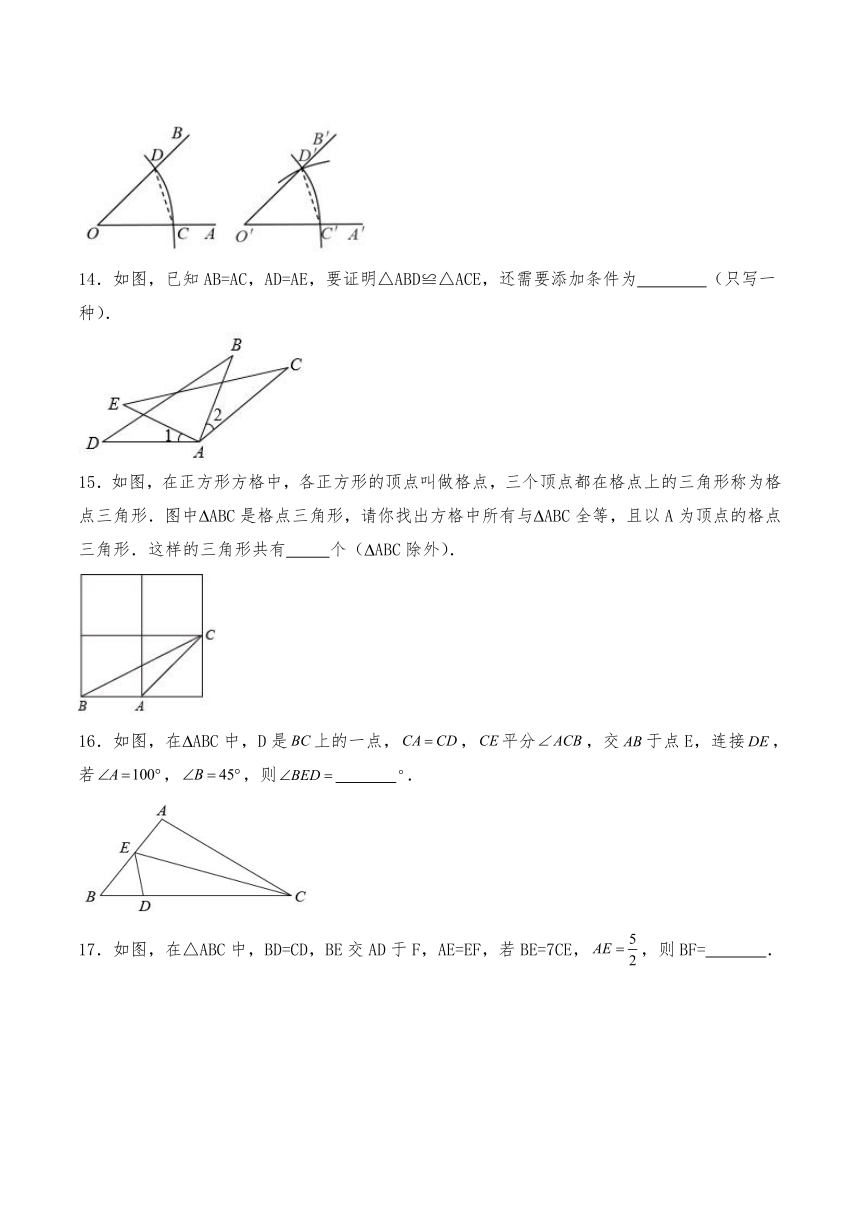
14.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,还需要添加条件为 (只写一种).
15.如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中 ABC是格点三角形,请你找出方格中所有与 ABC全等,且以A为顶点的格点三角形.这样的三角形共有 个( ABC除外).
16.如图,在 ABC中,D是上的一点,,平分,交于点E,连接,若,,则 .
17.如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,,则BF= .
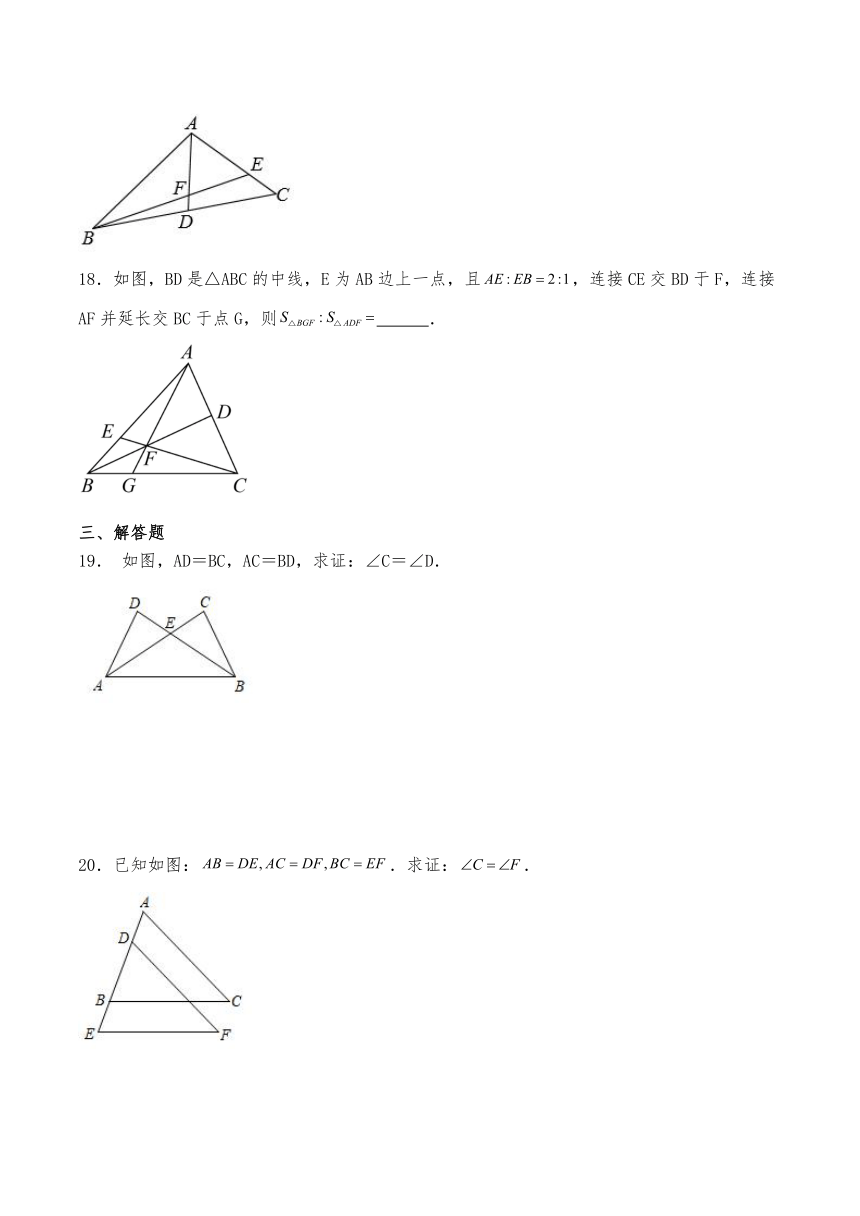
18.如图,BD是△ABC的中线,E为AB边上一点,且,连接CE交BD于F,连接AF并延长交BC于点G,则 .
三、解答题
19. 如图,AD=BC,AC=BD,求证:∠C=∠D.
20.已知如图:.求证:.
21.如图,A,B,C,D依次在同一条直线上,,BF与EC相交于点M.求证:.
22.如图, ABC是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与 ABC全等的格点三角形.
(1)在图①中所画三角形与 ABC有一条公共边;
(2)在图②中所画三角形与 ABC有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
23.已知:如图,,,.求证:.
24.如图,已知:AB=AC,BD=CD,E为AD上一点.
(1)求证:△ABD≌△ACD;
(2)若∠BED=50°,求∠CED的度数.
25.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:
(1)BC=EF;
(2)BC∥EF.
26.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE交BA于点D,CE交BF于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
27.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
参考答案
一、单选题
1.B
【分析】根据,,正好是两边一夹角,即可得出答案.
【解析】解:∵在△ABO和△DCO中,,
∴,故B正确.
故选:B.
2.B
【分析】根据“SSS”证明,根据全等三角形的性质得出即可.
【解析】解:∵在和中,
∴(SSS),
∴,故B正确.
故选:B.
3.C
【分析】根据已知条件求得、、,由此即可判定求解.
【解析】解:∵平分,
∴,
在和中,
∴
故选C
4.C
【分析】根据,可得,再用SSS即可求解.
【解析】解:∵,
∴,即,
∵,
∴.
故选:C
5.A
【分析】利用SSS证明△ABC≌△ADC,可得答案.
【解析】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS).
故选:A.
6.C
【解析】由题意根据等式的性质得出BC=EF,进而利用SSS证明△ABC与△DEF全等,利用全等三角形的性质得出∠ACB=∠DFE,最后利用三角形内角和进行分析解答.
【分析】解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴2∠DFE=180°﹣∠FGC,
故选:C.
7.D
【分析】连接CE,CD,可根据SSS证明△OCE≌△OCD,由此得到答案.
【解析】解:连接CE,CD,
由题意知,OE=OD,CE=CD,
∵OC=OC,
∴可根据SSS证明△OCE≌△OCD,
故选:D.
8.B
【分析】先证明BD=CE,然后证明△ADB≌△AEC,∠ADE=∠AED=70°,得到∠BAD=∠CAE,根据三角形内角和定理求出∠DAE=40°,从而求出∠BAD的度数即可得到答案.
【解析】解:∵BE=CD,
∴BE- DE=CD -DE,即BD=CE,
∵∠1=∠2=110°,AD=AE,
∴△ADB≌△AEC(SAS),∠ADE=∠AED=70°,
∴∠BAD=∠CAE,∠DAE=180°-∠ADE-∠AED=40°,
∵∠BAE=60°,
∴∠BAD=∠CAE=20°,
∴∠BAC=80°,
故选B.
9.D
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系:三角形两边之和大于第三边,两边之差小于第三边即可求解.
【解析】解:延长AD至E,使DE=AD,连接CE.
∵AD是边BC的中线,
∴BD=CD,
在△ABD和△ECD中
,
∴△ABD≌△ECD(SAS),
∴CE=AB=7.
在△ACE中,CE﹣AC<AE<CE+AC,
即:2<2AD<12,
1<AD<6.
故选:D.
10.D
【分析】由角度数量关系与三角形内角和定理可得,,由线段的数量关系可得,,进而可证明三角形全等.
【解析】解:∵,
∴,
∵
①+②得
②-①得
∴在 ABC和中,
∵
∴
故选D.
二、填空题
11.SSS
【解析】试题分析:因为△ABD和△ACD中,AB=AC,BD=CD,AD=AD,所以由SSS可证△ABD≌△ACD.
12.
【分析】根据已有的一边与一角对应相等,利用SAS判定两三角形确定,即可添加AC=BD即可
【解析】解:∵△ABC与△BAD,具有AB=BA,和,一边和一角对应相等,
根据SAS判定两三角形确定,需添加夹角的另一边,
∴添加AC=BD,
在△ABC和△BAD中,
,
∴
故答案是:AC=BD.
13.SSS
【分析】我们可以通过其作图的步骤来进行分析,作图时满足了三条边对应相等,于是我们可以判定是运用SSS,答案可得.
【解析】解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′B′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
显然运用的判定方法是SSS.
故答案为:SSS.
14.(答案不唯一)
【分析】根据已知条件选择合适的全等三角形的判定方法,添加合适的条件即可.
【解析】解:添加条件为,理由是:
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS).
故答案为:
15.5
【分析】根据全等三角形的判定及方格图的特征.认真观察图形可得答案.
【解析】解:如图,
根据平移,对称,可得与△ABC全等的三角形有5个,包括△ADE,△ANF,△ANG,△ACG,△AEF.
故答案为:5.
16.55°
【分析】根据SAS证明△ACE≌△DCE,根据全等三角形的性质可得∠CDE=∠A=100°,再根据三角形外角的性质可求∠BED.
【解析】解:∵CE平分∠ACB,
∴∠ACE=∠DCE,
在△ACE与△DCE中,
,
∴△ACE≌△DCE(SAS),
∴∠CDE=∠A=100°,
∵∠B=45°,
∴∠BED=∠CDE-∠B=100°-45°=55°,
故答案为:55°.
17.
【分析】延长AD至G,使DG=AD,连接BG,可证明,则BG=AC,,根据AE=EF,得到,可证出,即得出AC=BF,从而得出BF的长.
【解析】解:如图,延长AD至G,使DG=AD,连接BG,
在和中,
∴
∴BG=AC,,
又∵AE=EF,
∴,
又∵,
∴,
∴,
∴BG=BF,
∴AC=BF,
又∵BE=7CE,AE=,
∴BF+EF=,
即BF+=,
解得BF=.
故答案为:
18.
【分析】作,交于,作,交于.通过平行线的性质证明,,,即可求出.
【解析】解:作,交于,作,交于,
∵BD是的中线,
,
,,
,
,
,
,
,
,
在和中,
,
,
,,
,
,
,
,
故答案为:.
三、解答题
19. 证明:在△ABD和△BAC中,
∵,
∴△ABD≌△BAC(SSS),
∴∠C=∠D.
20.证明:,
,
21.证明:,
,
.
在和中,
,
.
22.(1)如图①所示,△ABD即为所求;
(2)如图②所示,△DEC即为所求;
(3)
如图③所示,△AED即为所求,
23.证明:∵,
∴,
∴,
又∵,,
∴(SAS),
∴.
24.(1)证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS);
(2)解:∵△ABD≌△ACD,
∴∠ADB=∠ADC,
在△EDB和△EDC中,
,
∴△EDB≌△EDC(SAS),
∴∠BED=∠CED,
∵∠BED=50°,
∴∠CED=∠BED=50°.
25.(1)证明:(1),
,
,
,
在 ABC与 中
,
,
.
(2)(2),
,
.
26.证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF,
在△ABF和△AEC中,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,由(1)得:△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∴∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=90°,
∴EC⊥BF.
27.(1)解:在△ABC中,∵∠A=80°,
∴,
∠ABC、∠ACB的平分线交于点D,
,
,
∠EDC
;
(2)解:在线段上取一点,使,连接,如图所示:
平分,
,
在和中,
,
,
,
,
,
为的一个外角,
,
为的一个外角,
,
平分,
,
,
∠A=2∠BDF,
在和中,
,
,
,
,
.
一、单选题
1.如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
2.如图,和中,,,若,则等于( )
A.10° B.20° C.30° D.40°
3.如图,已知平分,那么就可以证明,理由是( )
A. B. C. D.
4.如图,已知,则的理由是( )
A. B. C. D.
5.如图,这是一个平分角的仪器,,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证,从而得到AC就是这个角的平分线.其中证明的数学依据是( )
A.SSS B.ASA C.SAS D.AAS
6.如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是( )
A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B
7.作∠AOB的角平分线的作图过程如下:
用下面的三角形全等判定方法解释其作图原理,最为恰当的是( )
A.边角边 B.角边角 C.角角边 D.边边边
8.如图,在 ABC中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
9.在△ABC中,AB=7,AC=5,AD是边BC的中线,那么AD的取值范围是( )
A.0<AD<12 B.2<AD<12 C.0<AD<6 D.1<AD<6
10.在 ABC和中,,,,,则这两个三角形的关系是( )
A.不一定全等 B.不全等 C.根据“ASA”全等 D.根据“SAS”全等
二、填空题
11.如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是 .
12.如图,已知,添加一个条件 ,使
13.如图,小明用直尺和圆规作一个角等于已知角,则说明≌的依据是 .
14.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,还需要添加条件为 (只写一种).
15.如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中 ABC是格点三角形,请你找出方格中所有与 ABC全等,且以A为顶点的格点三角形.这样的三角形共有 个( ABC除外).
16.如图,在 ABC中,D是上的一点,,平分,交于点E,连接,若,,则 .
17.如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,,则BF= .
18.如图,BD是△ABC的中线,E为AB边上一点,且,连接CE交BD于F,连接AF并延长交BC于点G,则 .
三、解答题
19. 如图,AD=BC,AC=BD,求证:∠C=∠D.
20.已知如图:.求证:.
21.如图,A,B,C,D依次在同一条直线上,,BF与EC相交于点M.求证:.
22.如图, ABC是格点三角形(顶点在网格线的交点上),请在下列每个方格纸上按要求画一个与 ABC全等的格点三角形.
(1)在图①中所画三角形与 ABC有一条公共边;
(2)在图②中所画三角形与 ABC有一个公共角;
(3)在图③中所画三角形与△有且只有一个公共顶点.
23.已知:如图,,,.求证:.
24.如图,已知:AB=AC,BD=CD,E为AD上一点.
(1)求证:△ABD≌△ACD;
(2)若∠BED=50°,求∠CED的度数.
25.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:
(1)BC=EF;
(2)BC∥EF.
26.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,CE交BA于点D,CE交BF于点M.
求证:(1)EC=BF;
(2)EC⊥BF.
27.如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
参考答案
一、单选题
1.B
【分析】根据,,正好是两边一夹角,即可得出答案.
【解析】解:∵在△ABO和△DCO中,,
∴,故B正确.
故选:B.
2.B
【分析】根据“SSS”证明,根据全等三角形的性质得出即可.
【解析】解:∵在和中,
∴(SSS),
∴,故B正确.
故选:B.
3.C
【分析】根据已知条件求得、、,由此即可判定求解.
【解析】解:∵平分,
∴,
在和中,
∴
故选C
4.C
【分析】根据,可得,再用SSS即可求解.
【解析】解:∵,
∴,即,
∵,
∴.
故选:C
5.A
【分析】利用SSS证明△ABC≌△ADC,可得答案.
【解析】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS).
故选:A.
6.C
【解析】由题意根据等式的性质得出BC=EF,进而利用SSS证明△ABC与△DEF全等,利用全等三角形的性质得出∠ACB=∠DFE,最后利用三角形内角和进行分析解答.
【分析】解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,
∴2∠DFE=180°﹣∠FGC,
故选:C.
7.D
【分析】连接CE,CD,可根据SSS证明△OCE≌△OCD,由此得到答案.
【解析】解:连接CE,CD,
由题意知,OE=OD,CE=CD,
∵OC=OC,
∴可根据SSS证明△OCE≌△OCD,
故选:D.
8.B
【分析】先证明BD=CE,然后证明△ADB≌△AEC,∠ADE=∠AED=70°,得到∠BAD=∠CAE,根据三角形内角和定理求出∠DAE=40°,从而求出∠BAD的度数即可得到答案.
【解析】解:∵BE=CD,
∴BE- DE=CD -DE,即BD=CE,
∵∠1=∠2=110°,AD=AE,
∴△ADB≌△AEC(SAS),∠ADE=∠AED=70°,
∴∠BAD=∠CAE,∠DAE=180°-∠ADE-∠AED=40°,
∵∠BAE=60°,
∴∠BAD=∠CAE=20°,
∴∠BAC=80°,
故选B.
9.D
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系:三角形两边之和大于第三边,两边之差小于第三边即可求解.
【解析】解:延长AD至E,使DE=AD,连接CE.
∵AD是边BC的中线,
∴BD=CD,
在△ABD和△ECD中
,
∴△ABD≌△ECD(SAS),
∴CE=AB=7.
在△ACE中,CE﹣AC<AE<CE+AC,
即:2<2AD<12,
1<AD<6.
故选:D.
10.D
【分析】由角度数量关系与三角形内角和定理可得,,由线段的数量关系可得,,进而可证明三角形全等.
【解析】解:∵,
∴,
∵
①+②得
②-①得
∴在 ABC和中,
∵
∴
故选D.
二、填空题
11.SSS
【解析】试题分析:因为△ABD和△ACD中,AB=AC,BD=CD,AD=AD,所以由SSS可证△ABD≌△ACD.
12.
【分析】根据已有的一边与一角对应相等,利用SAS判定两三角形确定,即可添加AC=BD即可
【解析】解:∵△ABC与△BAD,具有AB=BA,和,一边和一角对应相等,
根据SAS判定两三角形确定,需添加夹角的另一边,
∴添加AC=BD,
在△ABC和△BAD中,
,
∴
故答案是:AC=BD.
13.SSS
【分析】我们可以通过其作图的步骤来进行分析,作图时满足了三条边对应相等,于是我们可以判定是运用SSS,答案可得.
【解析】解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′B′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
显然运用的判定方法是SSS.
故答案为:SSS.
14.(答案不唯一)
【分析】根据已知条件选择合适的全等三角形的判定方法,添加合适的条件即可.
【解析】解:添加条件为,理由是:
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS).
故答案为:
15.5
【分析】根据全等三角形的判定及方格图的特征.认真观察图形可得答案.
【解析】解:如图,
根据平移,对称,可得与△ABC全等的三角形有5个,包括△ADE,△ANF,△ANG,△ACG,△AEF.
故答案为:5.
16.55°
【分析】根据SAS证明△ACE≌△DCE,根据全等三角形的性质可得∠CDE=∠A=100°,再根据三角形外角的性质可求∠BED.
【解析】解:∵CE平分∠ACB,
∴∠ACE=∠DCE,
在△ACE与△DCE中,
,
∴△ACE≌△DCE(SAS),
∴∠CDE=∠A=100°,
∵∠B=45°,
∴∠BED=∠CDE-∠B=100°-45°=55°,
故答案为:55°.
17.
【分析】延长AD至G,使DG=AD,连接BG,可证明,则BG=AC,,根据AE=EF,得到,可证出,即得出AC=BF,从而得出BF的长.
【解析】解:如图,延长AD至G,使DG=AD,连接BG,
在和中,
∴
∴BG=AC,,
又∵AE=EF,
∴,
又∵,
∴,
∴,
∴BG=BF,
∴AC=BF,
又∵BE=7CE,AE=,
∴BF+EF=,
即BF+=,
解得BF=.
故答案为:
18.
【分析】作,交于,作,交于.通过平行线的性质证明,,,即可求出.
【解析】解:作,交于,作,交于,
∵BD是的中线,
,
,,
,
,
,
,
,
,
在和中,
,
,
,,
,
,
,
,
故答案为:.
三、解答题
19. 证明:在△ABD和△BAC中,
∵,
∴△ABD≌△BAC(SSS),
∴∠C=∠D.
20.证明:,
,
21.证明:,
,
.
在和中,
,
.
22.(1)如图①所示,△ABD即为所求;
(2)如图②所示,△DEC即为所求;
(3)
如图③所示,△AED即为所求,
23.证明:∵,
∴,
∴,
又∵,,
∴(SAS),
∴.
24.(1)证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS);
(2)解:∵△ABD≌△ACD,
∴∠ADB=∠ADC,
在△EDB和△EDC中,
,
∴△EDB≌△EDC(SAS),
∴∠BED=∠CED,
∵∠BED=50°,
∴∠CED=∠BED=50°.
25.(1)证明:(1),
,
,
,
在 ABC与 中
,
,
.
(2)(2),
,
.
26.证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF,
在△ABF和△AEC中,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,由(1)得:△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∴∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=90°,
∴EC⊥BF.
27.(1)解:在△ABC中,∵∠A=80°,
∴,
∠ABC、∠ACB的平分线交于点D,
,
,
∠EDC
;
(2)解:在线段上取一点,使,连接,如图所示:
平分,
,
在和中,
,
,
,
,
,
为的一个外角,
,
为的一个外角,
,
平分,
,
,
∠A=2∠BDF,
在和中,
,
,
,
,
.
同课章节目录
